git常用命令和开发常用场景
git命令
git init
创建一个空的git仓库或者重新初始化已有仓库
git clone [url]
将存储库克隆到新目录
git add
添加内容到索引
git status
显示工作树状态
git commit -m ""
记录仓库的修改
git reset
重置当前HEAD到指定的状态
git reset –-soft:回退到某个版本,只回退了commit的信息,不会恢复到index file一级。如果还要提交,直接commit即可
git reset –-mixed:回退到某个版本,只回退了commit的信息,并且恢复到index file一级。如果还要提交,需要重新add,再commit即可
git reset -–hard:彻底回退到某个版本,本地的源码也会变为上一个版本的内容(误操作后需要学git reflog挽救),撤销的commit中所包含的更改被冲掉
git branch -m改名 -c 复制分支 -d删除上游分支 -r删除远程分支
列出、创建或删除分支
git checkout -b创建并切换
选择分支或者恢复工作树文件
git merge
合并多条历史提交描述记录
git log
显示提交日志
git stash
将变化藏在一个脏工作区中
git tag
创建、列出、删除或验证使用GPG签名的tag对象
git fetch
用于从远程仓库获取最新的提交历史和分支信息,但并不自动合并或修改本地代码。
1. 检查远程仓库是否有新的提交或分支。
2. 获取远程仓库的最新提交历史,但不会应用到当前工作目录中。
3. 更新本地仓库的远程分支指针,指向远程仓库的最新提交。
git pull <远程主机名> <远程分支名>:<本地分支名>
用于从远程获取代码并合并本地的版本。
git push <远程主机名> <本地分支名>:<远程分支名>
用于从将本地的分支版本上传到远程并合并。
git cherry-pick <commitHash>
这个命令的作用就是把指定的commit,拉到一个新的分支上。
三人合作开发项目git命令实例
-
克隆(Clone)远程仓库:
git clone <远程仓库URL> -
创建自己分支(Branch):
git branch <分支名> git checkout -b dev origin/dev -
切换到自己的分支:
git checkout <分支名> -
查看状态(status)添加(Add)和提交(Commit)更改:
git status git add <文件名> 或者 git add . 提交所有 git commit -m "提交信息" -
拉取(Pull)远程仓库的更改:
git pull origin <分支名>如果
git pull提示no tracking information,则说明本地分支和远程分支的链接关系没有创建,用命令git branch --set-upstream-to <branch-name> origin/<branch-name> -
解决冲突(Conflict):
当合并分支时出现冲突时,手动解决冲突并提交更改。 -
推送(Push)更改到远程仓库自己的分支:
git push origin <分支名> -
成功推送之后在远程仓库提交合并请求到主分支
版本回退
1.查看提交历史,选择要回退的版本
git log
2.回退版本
git reset --hard commit_id
3.如果后悔,想要重返未来
git reflog 查看命令历史 确定回到未来的哪个版本
git reset –-soft:回退到某个版本,只回退了commit的信息,不会恢复到index file一级。如果还要提交,直接commit即可
git reset –-mixed:回退到某个版本,只回退了commit的信息,并且恢复到index file一级。如果还要提交,需要重新add,再commit即可
git reset -–hard:彻底回退到某个版本,本地的源码也会变为上一个版本的内容(误操作后需要学git reflog挽救),撤销的commit中所包含的更改被冲掉
Bug分支场景
模拟场景:当你接到一个修复一个代号101的bug的任务在master分支上,很自然地,你想创建一个分支issue-101来修复它,但是,等等,当前正在dev上进行的工作还没有提交
1.把当前工作现场储藏起来
git stash
2.修复bug
git checkout master
git checkout -b issue-101
git add .
git commit -m "fix bug 101"
//[issue-101 4c805e2] fix bug 101
git switch master
git merge --no-ff -m "merged bug fix 101" issue-101
3.继续开发dev
git switch dev
git status
git stash listgit stash apply + git stash drop / git stash pop
git stash list
场景:同样的bug,要在dev上修复,我们只需要把4c805e2 fix bug 101这个提交所做的修改“复制”到dev分支。注意:我们只想复制4c805e2 fix bug 101这个提交所做的修改,并不是把整个master分支merge过来。
$ git branch
* devmaster
$ git cherry-pick 4c805e2
[master 1d4b803] fix bug 101
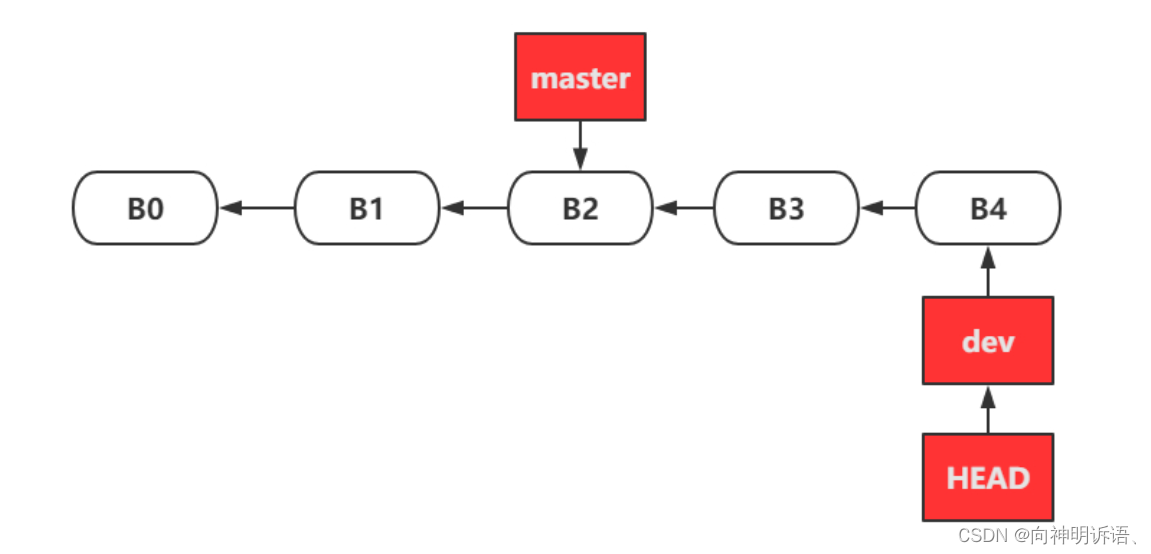
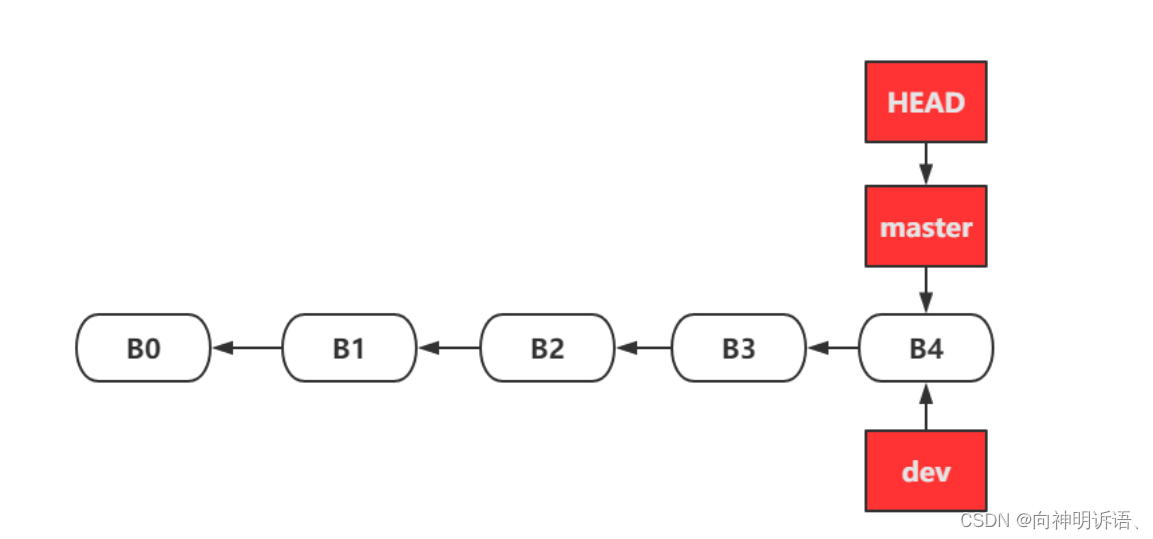
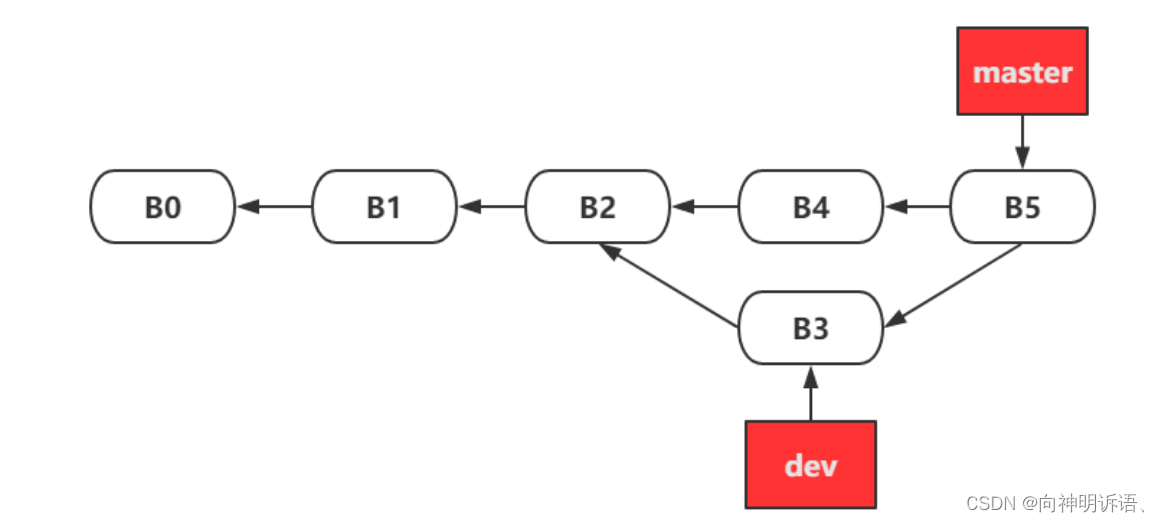
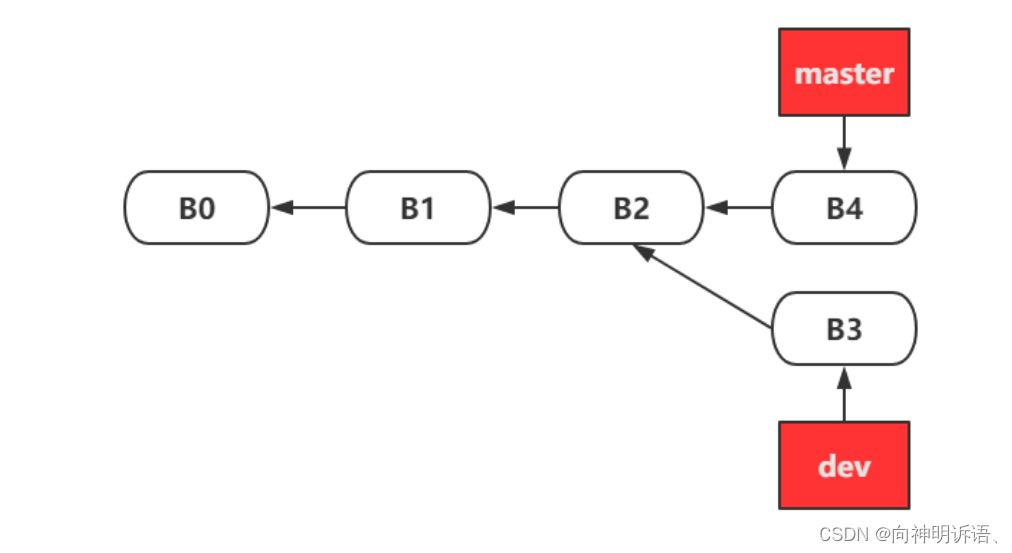
git merge三种使用场景
命令都是一样的开发完dev分支然后切回master分支之后
git merge dev
只不过第三种会报错需要在master分支上解决冲突之后自行提交一次就ok
1.快进(无冲突
2.非快进(无冲突
3.非快进(有冲突
相关文章:

git常用命令和开发常用场景
git命令 git init 创建一个空的git仓库或者重新初始化已有仓库 git clone [url] 将存储库克隆到新目录 git add 添加内容到索引 git status 显示工作树状态 git commit -m "" 记录仓库的修改 git reset 重置当前HEAD到指定的状态 git reset –-soft:…...

02 认识Verilog HDL
02 认识Verilog HDL 对于Verilog的语言的学习,我认为没必要一开始就从头到尾认真的学习这个语言,把这个语言所有细节都搞清楚也不现实,我们能够看懂当前FPGA的代码的程度就可以了,随着学习FPGA深度的增加,再不断的…...

解决VUE安装依赖时报错:npm ERR! code ERESOLVE
前言 在使用 npm 安装项目依赖时,有时会遇到错误信息 “npm ERR! code ERESOLVE”,该错误通常发生在依赖版本冲突或者依赖解析问题时。本文将详细介绍出现这个错误的原因,并提供解决方法,确保正确安装项目依赖并避免该错误的发生。…...

软件公司的项目管理软件选择指南
我们经常在项目推进中经常遇到各种各样的问题,最常见的是因团队工作效率低而无法在截止日期之前按时完成工作。但是如果能合理使用项目管理软件,可以有效监控项目进程,提高工作效率,从而保证按时完成任务。那么软件公司适合什么项…...

2、服务器安装docker
# 1.卸载旧的版本 yum remove -y docker \ docker-client\ docker-client-latest\ docker-common docker-latest\ docker-latest-logrotate\ docker-logrotate docker-s…...

UDP报文结构
文章目录 一、UDP报头1.1源端口号1.2目的端口号1.3UDP报文长度1.4UDP校验和(checksum) UDP报头和UDP载荷(payload)之间的拼接可以认为是一个“字符串拼接”,里面是二进制数据。 一、UDP报头 UDP报头分成4个部分,每个部分2个字节。分别是: 1…...

(高阶) Redis 7 第21讲 IO多路复用模型 完结篇
🌹 以下分享 Redis IO多路复用模型,如有问题请指教。🌹🌹 如你对技术也感兴趣,欢迎交流。🌹🌹🌹 如有对阁下帮助,请👍点赞💖收藏🐱🏍分享😀 IO多路复用模型是什么 I/O:网络IO 多路:多个客户端连接(连接即套接字描述符,即socket或channel),指…...

2023年入职/转行网络安全,该如何规划?
前言 前段时间,知名机构麦可思研究院发布了 《2022年中国本科生就业报告》,其中详细列出近五年的本科绿牌专业,其中,信息安全位列第一。 网络安全前景 对于网络安全的发展与就业前景,想必无需我多言,作为…...

解密RabbitMQ:你所不知道的端口及其重要性
解密RabbitMQ:你所不知道的端口及其重要性 前言第一部分:AMQP默认端口(5672)第二部分:RabbitMQ管理界面端口(15672)第三部分:Erlang Port Mapper Daemon(epmd)端口(4369&…...
)
Docker 环境搭建 (centeros)
CentOS环境下安装Docker 本文档将指导您在CentOS操作系统上安装Docker。Docker是一个开源的容器化平台,可以帮助您轻松地创建、部署和管理容器化应用程序。 步骤1:更新系统 在安装Docker之前,首先确保您的系统已经更新到最新版本。打开终端…...
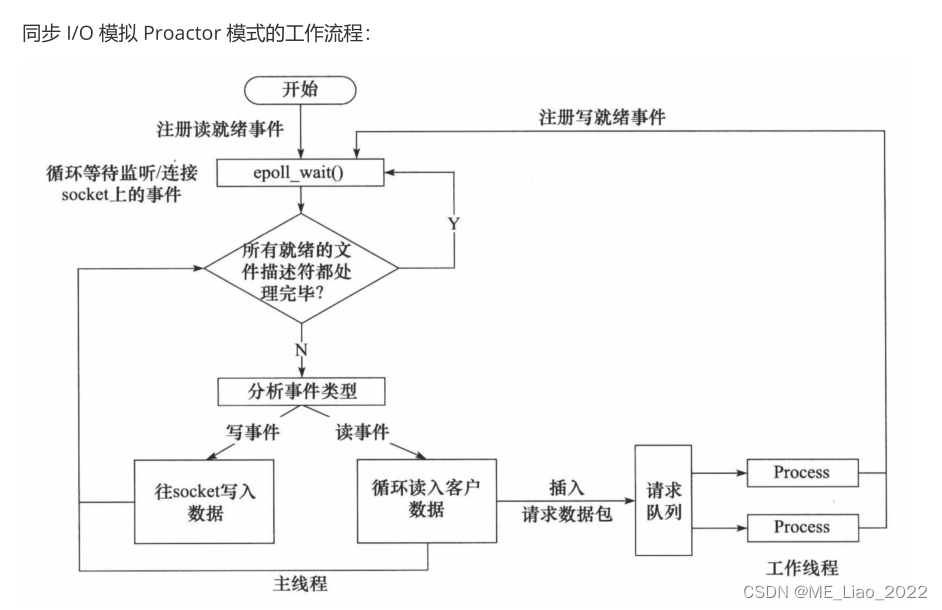
服务器编程基本框架
服务器编程基本框架 虽然服务器程序种类繁多,但其基本框架都一样,不同之处在于逻辑处理。 I/O 处理单元是服务器管理客户连接的模块。它通常要完成以下工作:等待并接受新的客户连接,接收客户数据,将服务器响应数据返回…...

Leetcode——数组的遍历系列练习
485. 最大连续 1 的个数 class Solution { public:int findMaxConsecutiveOnes(vector<int>& nums) {// 记录最大连续1个数int max 0;// 记录数组中存在1个数int sum 0;// 遍历连续1个数int count 0;for (int i 0; i < nums.size() - 1; i) {if (nums[i] 1)s…...
免费的ChatGPT与StableDiffusion AI绘画 二合一 附在线地址
ChatGPT与StableDiffusion 在线地址在文末 介绍 嘿,大家好!今天我要给大家介绍一个非常酷炫的技术结合——ChatGPT与StableDiffusion的合作。听起来是不是很有趣?那么,让我们一起来看看这个组合到底能带给我们什么样的奇妙体验…...
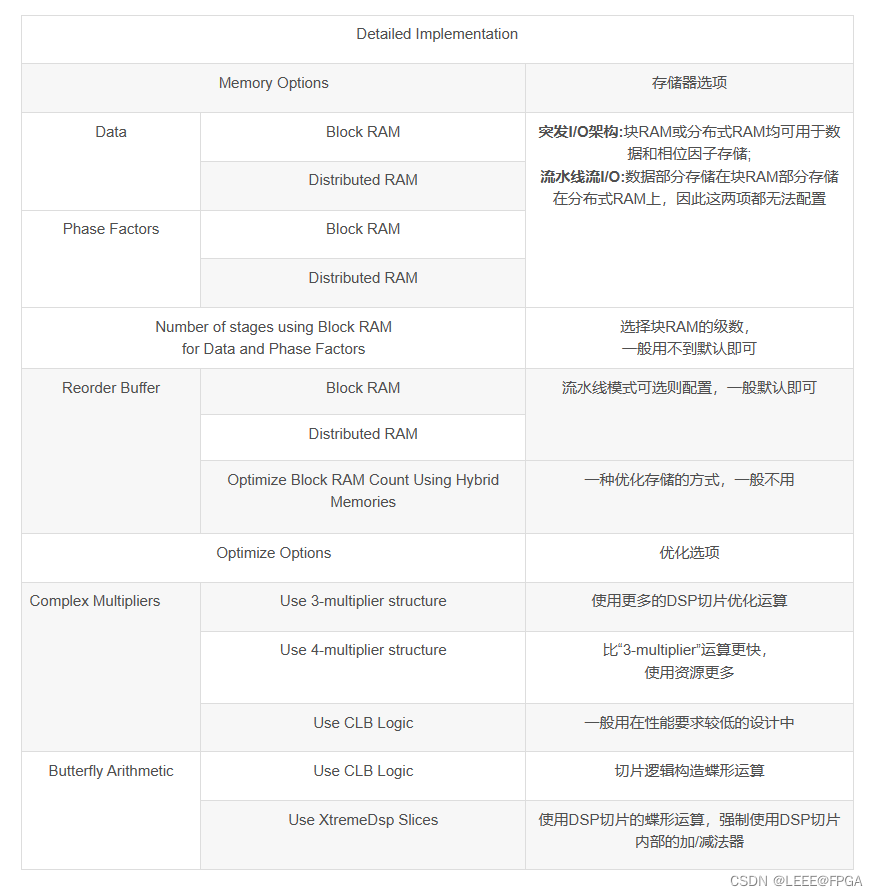
vivado FFT IP仿真(3)FFT IP选项说明
xilinx FFT IP手册PG109 1 Configuration 2 Implementation 3 Detailed Implementation IP Symbol...

正点原子嵌入式linux驱动开发——Busybox根文件系统构建
前面已经移植了TF-A、Uboot和Linux kernel,就剩最后一个 rootfs(根文件系统)了,本章就来学习一下根文件系统的组成以及如何构建根文件系统。这是Linux系统移植的最后一步,根文件系统构建好以后就意味着拥有了一个完整的、可以运行的最小系统 …...

React闭包
声明 本文将深入探讨React与闭包之间的关系。 我们将首先介绍React和闭包的基本概念,然后详细解释React组件中如何使用闭包来处理状态和作用域的问题。 通过本文的阅读,你将对React中闭包的概念有更深入的理解,并能够在开发React应用时更好地…...
【VS Code】推荐一套我非常喜欢的主题和字体样式
话不多说,先上样式: 这里我的主题是 One Dark Pro,也是 VS Code 里面使用非常多的主题之一。直接安装插件即可使用。 我的字体是 JetBrains Mono,虽然使用的是 VS Code,但还是喜欢 webstorm 的字体。我们可以直接去官网…...
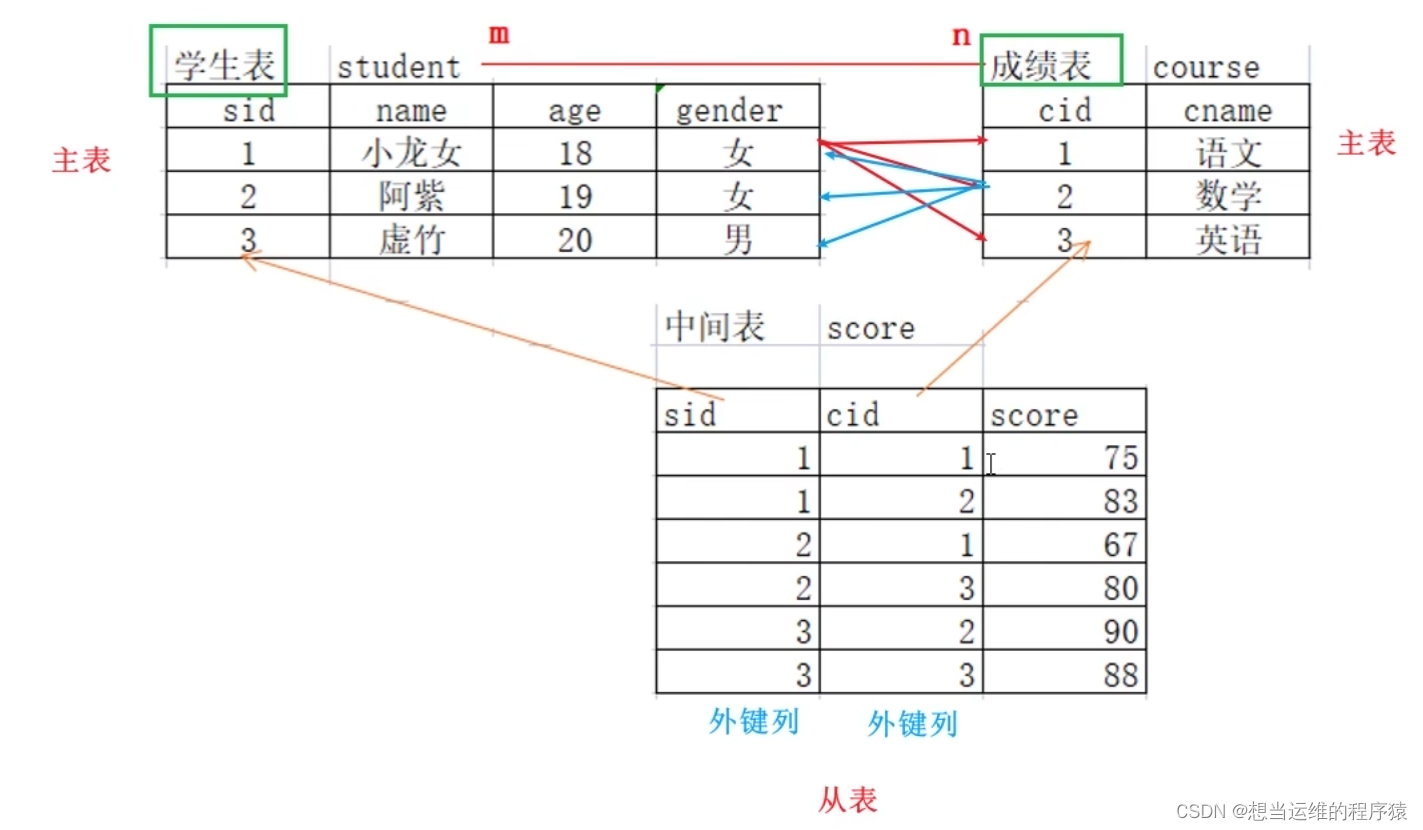
【SQL】MySQL中的约束
1. 主键约束(primary key): 相当于唯一约束非空约束分为单列主键,多列联合主键,一个表只有一个主键多列联合主键的每列都不能为空 2. 自增长约束(auto_increment): 用在单列主键后…...

css div左右布局
div左右布局 htm代码 <div class"content-box"><div class"left"></div><div class"right"></div></div>css样式 .content-box{height: 100%;width: 100%;display: flex; } .left{display: block;width:…...
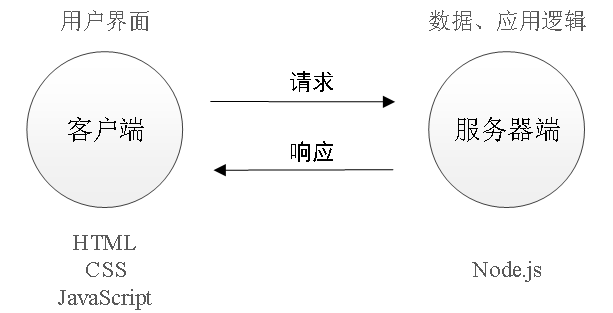
06_Node.js服务器开发
1 服务器开发的基本概念 1.1 为什么学习服务器开发 Node.js开发属于服务器开发,那么作为一名前端工程师为什么需要学习服务器开发呢? 为什么学习服务器开发? 能够和后端程序员更加紧密配合网站业务逻辑前置扩宽知识视野 1.2 服务器开发可…...

装饰模式(Decorator Pattern)重构java邮件发奖系统实战
前言 现在我们有个如下的需求,设计一个邮件发奖的小系统, 需求 1.数据验证 → 2. 敏感信息加密 → 3. 日志记录 → 4. 实际发送邮件 装饰器模式(Decorator Pattern)允许向一个现有的对象添加新的功能,同时又不改变其…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

苍穹外卖--缓存菜品
1.问题说明 用户端小程序展示的菜品数据都是通过查询数据库获得,如果用户端访问量比较大,数据库访问压力随之增大 2.实现思路 通过Redis来缓存菜品数据,减少数据库查询操作。 缓存逻辑分析: ①每个分类下的菜品保持一份缓存数据…...

PL0语法,分析器实现!
简介 PL/0 是一种简单的编程语言,通常用于教学编译原理。它的语法结构清晰,功能包括常量定义、变量声明、过程(子程序)定义以及基本的控制结构(如条件语句和循环语句)。 PL/0 语法规范 PL/0 是一种教学用的小型编程语言,由 Niklaus Wirth 设计,用于展示编译原理的核…...

Python如何给视频添加音频和字幕
在Python中,给视频添加音频和字幕可以使用电影文件处理库MoviePy和字幕处理库Subtitles。下面将详细介绍如何使用这些库来实现视频的音频和字幕添加,包括必要的代码示例和详细解释。 环境准备 在开始之前,需要安装以下Python库:…...

九天毕昇深度学习平台 | 如何安装库?
pip install 库名 -i https://pypi.tuna.tsinghua.edu.cn/simple --user 举个例子: 报错 ModuleNotFoundError: No module named torch 那么我需要安装 torch pip install torch -i https://pypi.tuna.tsinghua.edu.cn/simple --user pip install 库名&#x…...

服务器--宝塔命令
一、宝塔面板安装命令 ⚠️ 必须使用 root 用户 或 sudo 权限执行! sudo su - 1. CentOS 系统: yum install -y wget && wget -O install.sh http://download.bt.cn/install/install_6.0.sh && sh install.sh2. Ubuntu / Debian 系统…...

sipsak:SIP瑞士军刀!全参数详细教程!Kali Linux教程!
简介 sipsak 是一个面向会话初始协议 (SIP) 应用程序开发人员和管理员的小型命令行工具。它可以用于对 SIP 应用程序和设备进行一些简单的测试。 sipsak 是一款 SIP 压力和诊断实用程序。它通过 sip-uri 向服务器发送 SIP 请求,并检查收到的响应。它以以下模式之一…...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

springboot整合VUE之在线教育管理系统简介
可以学习到的技能 学会常用技术栈的使用 独立开发项目 学会前端的开发流程 学会后端的开发流程 学会数据库的设计 学会前后端接口调用方式 学会多模块之间的关联 学会数据的处理 适用人群 在校学生,小白用户,想学习知识的 有点基础,想要通过项…...
