qt 关于自定义控件，然后其他页面提升后背景样式表不生效问题
一、自定义控件如果是widget ，需要再widget 里放一个QFrame ，在QFrame设置样式表背景才行
二、重写paintEvent
void Form::paintEvent(QPaintEvent *e)
{QStyleOption opt;opt.init(this);QPainter p(this);style()->drawPrimitive(QStyle::PE_Widget, &opt, &p, this);QWidget::paintEvent(e);
}相关文章：
qt 关于自定义控件，然后其他页面提升后背景样式表不生效问题
一、自定义控件如果是widget ，需要再widget 里放一个QFrame ，在QFrame设置样式表背景才行 二、重写paintEvent void Form::paintEvent(QPaintEvent *e) {QStyleOption opt;opt.init(this);QPainter p(this);style()->drawPrimitive(QStyle::PE_Widg…...
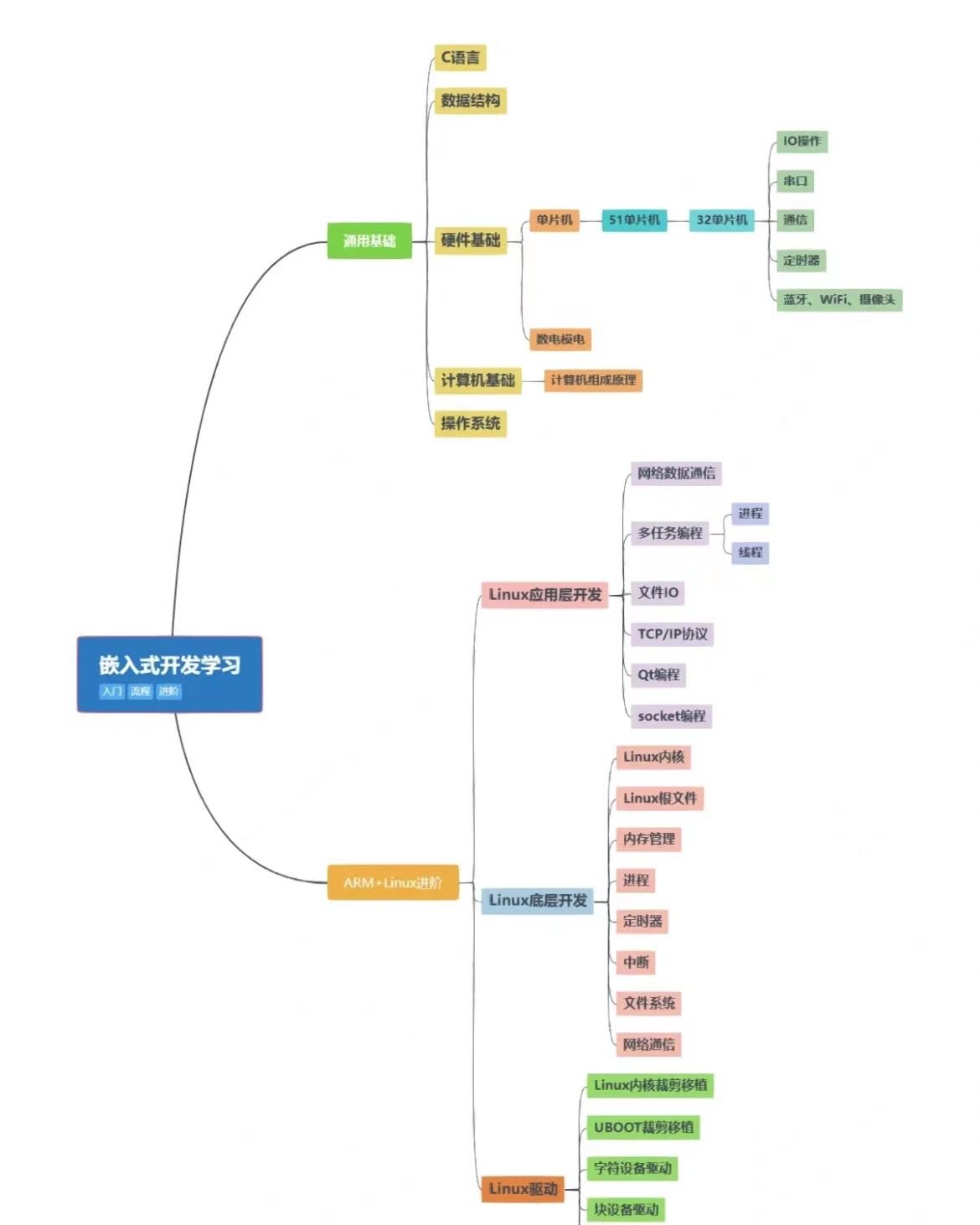
对比纯软开与嵌入式硬件开发谁更好呢？
对比纯软开与嵌入式硬件开发谁更好呢？ 你的纠结和犹豫是理解的，职业选择确实是一个重要的决策。我明白你在嵌入式和软件开发之间犹豫不决的原因。让我给你提供一些建议，帮助你做出更明智的决定。最近很多小伙伴找我，说想要一些嵌入…...
软考 系统架构设计师系列知识点之软件质量属性（5）
接前一篇文章：软考 系统架构设计师系列知识点之软件质量属性（4） 所属章节： 第8章. 系统质量属性与架构评估 第2节. 面向架构评估的质量属性 相关试题 5. 某公司欲开发一个网上商城系统。在架构设计阶段，公司的架构师…...
修改ubuntu服务器fs文件最大打开数
起因 在对项目进行压测的时候，请求异常 java.net.SocketException: socket closed，查看nginx代理服务器的日志。tail -f -n500 /var/log/nginx/error.log 显示 文件打开数太多socket() failed (24: Too many open files) while connecting to upstream …...
linux下Qt的pro文件
生成生成文件后缀名的说明。这只是泛泛而谈，实际发现跟编译器有关。比如在windows系统上用MinGW，可能静态库还是a后缀。 文件静态库动态库目标文件LINUXasooWINDOWSlibdllobj 在.pro文件中，INCLUDEPATH用于引入外部库的头文件，L…...
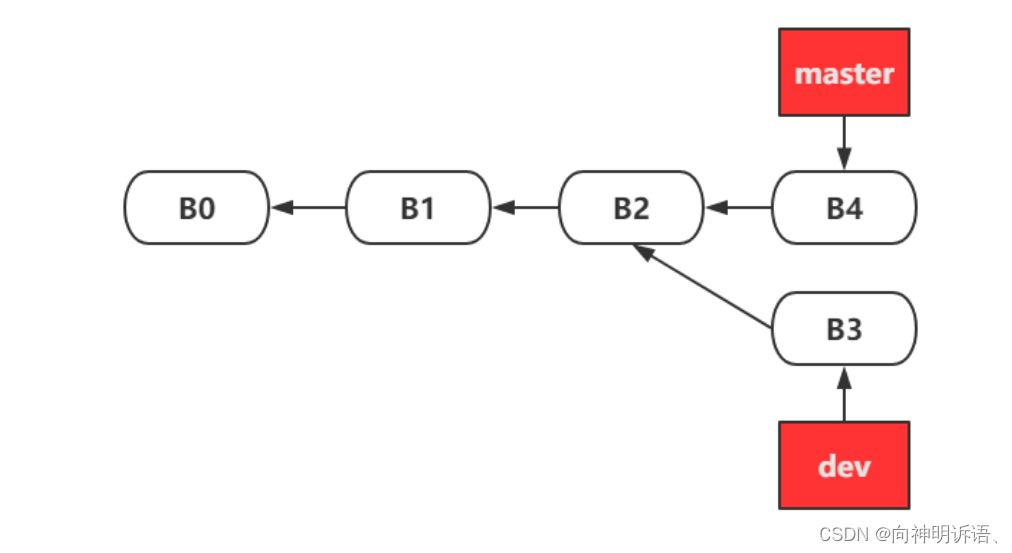
git常用命令和开发常用场景
git命令 git init 创建一个空的git仓库或者重新初始化已有仓库 git clone [url] 将存储库克隆到新目录 git add 添加内容到索引 git status 显示工作树状态 git commit -m "" 记录仓库的修改 git reset 重置当前HEAD到指定的状态 git reset –-soft：…...
02 认识Verilog HDL
02 认识Verilog HDL 对于Verilog的语言的学习，我认为没必要一开始就从头到尾认真的学习这个语言，把这个语言所有细节都搞清楚也不现实，我们能够看懂当前FPGA的代码的程度就可以了，随着学习FPGA深度的增加，再不断的…...
解决VUE安装依赖时报错：npm ERR! code ERESOLVE
前言 在使用 npm 安装项目依赖时，有时会遇到错误信息 “npm ERR! code ERESOLVE”，该错误通常发生在依赖版本冲突或者依赖解析问题时。本文将详细介绍出现这个错误的原因，并提供解决方法，确保正确安装项目依赖并避免该错误的发生。…...
软件公司的项目管理软件选择指南
我们经常在项目推进中经常遇到各种各样的问题，最常见的是因团队工作效率低而无法在截止日期之前按时完成工作。但是如果能合理使用项目管理软件，可以有效监控项目进程，提高工作效率，从而保证按时完成任务。那么软件公司适合什么项…...
2、服务器安装docker
# 1.卸载旧的版本 yum remove -y docker \ docker-client\ docker-client-latest\ docker-common docker-latest\ docker-latest-logrotate\ docker-logrotate docker-s…...
UDP报文结构
文章目录 一、UDP报头1.1源端口号1.2目的端口号1.3UDP报文长度1.4UDP校验和(checksum) UDP报头和UDP载荷(payload)之间的拼接可以认为是一个“字符串拼接”，里面是二进制数据。 一、UDP报头 UDP报头分成4个部分，每个部分2个字节。分别是： 1…...
(高阶) Redis 7 第21讲 IO多路复用模型 完结篇
🌹 以下分享 Redis IO多路复用模型，如有问题请指教。🌹🌹 如你对技术也感兴趣，欢迎交流。🌹🌹🌹 如有对阁下帮助，请👍点赞💖收藏🐱🏍分享😀 IO多路复用模型是什么 I/O：网络IO 多路：多个客户端连接（连接即套接字描述符，即socket或channel）,指…...
2023年入职/转行网络安全，该如何规划？
前言 前段时间，知名机构麦可思研究院发布了 《2022年中国本科生就业报告》，其中详细列出近五年的本科绿牌专业，其中，信息安全位列第一。 网络安全前景 对于网络安全的发展与就业前景，想必无需我多言，作为…...
解密RabbitMQ：你所不知道的端口及其重要性
解密RabbitMQ：你所不知道的端口及其重要性 前言第一部分：AMQP默认端口(5672)第二部分：RabbitMQ管理界面端口（15672）第三部分：Erlang Port Mapper Daemon（epmd）端口（4369&…...
Docker 环境搭建 （centeros）
CentOS环境下安装Docker 本文档将指导您在CentOS操作系统上安装Docker。Docker是一个开源的容器化平台，可以帮助您轻松地创建、部署和管理容器化应用程序。 步骤1：更新系统 在安装Docker之前，首先确保您的系统已经更新到最新版本。打开终端…...
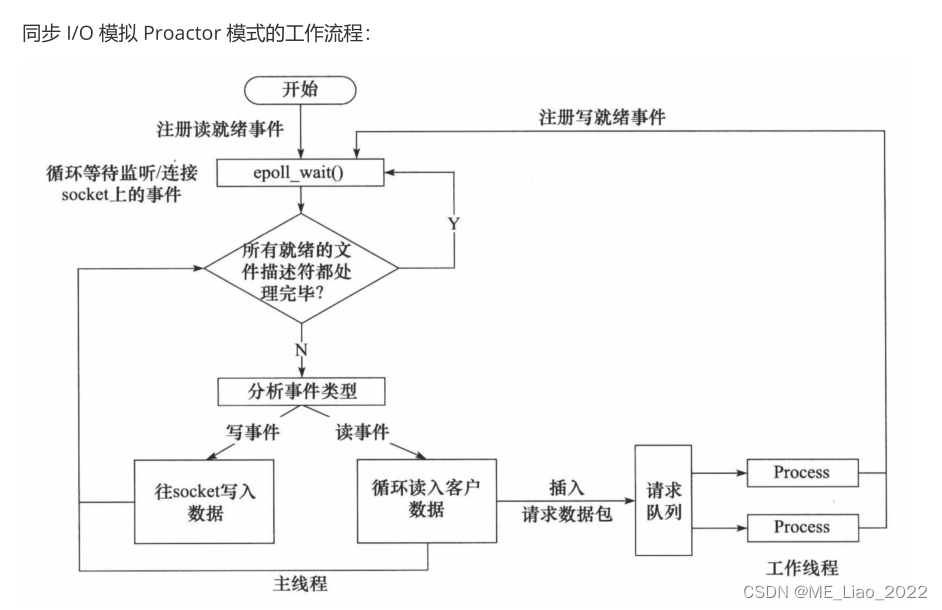
服务器编程基本框架
服务器编程基本框架 虽然服务器程序种类繁多，但其基本框架都一样，不同之处在于逻辑处理。 I/O 处理单元是服务器管理客户连接的模块。它通常要完成以下工作：等待并接受新的客户连接，接收客户数据，将服务器响应数据返回…...
Leetcode——数组的遍历系列练习
485. 最大连续 1 的个数 class Solution { public:int findMaxConsecutiveOnes(vector<int>& nums) {// 记录最大连续1个数int max 0;// 记录数组中存在1个数int sum 0;// 遍历连续1个数int count 0;for (int i 0; i < nums.size() - 1; i) {if (nums[i] 1)s…...
免费的ChatGPT与StableDiffusion AI绘画 二合一 附在线地址
ChatGPT与StableDiffusion 在线地址在文末 介绍 嘿，大家好！今天我要给大家介绍一个非常酷炫的技术结合——ChatGPT与StableDiffusion的合作。听起来是不是很有趣？那么，让我们一起来看看这个组合到底能带给我们什么样的奇妙体验…...
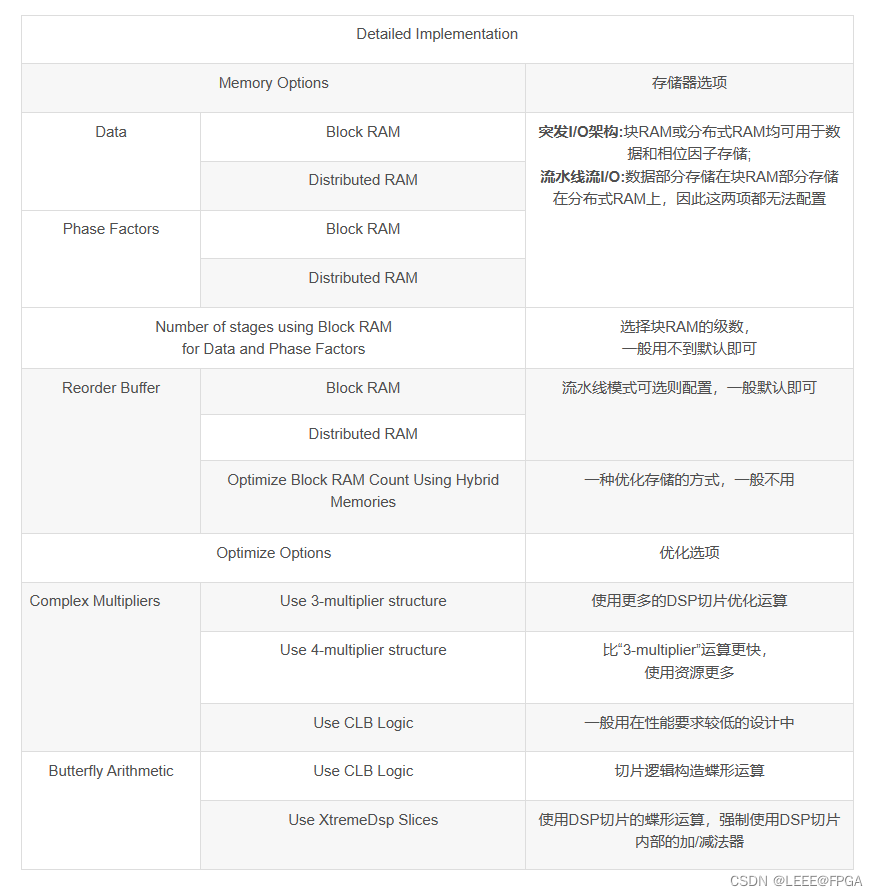
vivado FFT IP仿真（3）FFT IP选项说明
xilinx FFT IP手册PG109 1 Configuration 2 Implementation 3 Detailed Implementation IP Symbol...
正点原子嵌入式linux驱动开发——Busybox根文件系统构建
前面已经移植了TF-A、Uboot和Linux kernel，就剩最后一个 rootfs(根文件系统)了，本章就来学习一下根文件系统的组成以及如何构建根文件系统。这是Linux系统移植的最后一步，根文件系统构建好以后就意味着拥有了一个完整的、可以运行的最小系统 …...
19c补丁后oracle属主变化，导致不能识别磁盘组
补丁后服务器重启，数据库再次无法启动 ORA01017: invalid username/password; logon denied Oracle 19c 在打上 19.23 或以上补丁版本后，存在与用户组权限相关的问题。具体表现为，Oracle 实例的运行用户（oracle）和集…...
vscode里如何用git
打开vs终端执行如下： 1 初始化 Git 仓库（如果尚未初始化） git init 2 添加文件到 Git 仓库 git add . 3 使用 git commit 命令来提交你的更改。确保在提交时加上一个有用的消息。 git commit -m "备注信息" 4 …...
css实现圆环展示百分比，根据值动态展示所占比例
代码如下 <view class""><view class"circle-chart"><view v-if"!!num" class"pie-item" :style"{background: conic-gradient(var(--one-color) 0%,#E9E6F1 ${num}%),}"></view><view v-else …...
基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施，由雇主和个人按一定比例缴纳保险费，建立社会医疗保险基金，支付雇员医疗费用的一种医疗保险制度， 它是促进社会文明和进步的…...
【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装；只需暴露 19530（gRPC）与 9091（HTTP/WebUI）两个端口，即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...
服务器硬防的应用场景都有哪些？
服务器硬防是指一种通过硬件设备层面的安全措施来防御服务器系统受到网络攻击的方式，避免服务器受到各种恶意攻击和网络威胁，那么，服务器硬防通常都会应用在哪些场景当中呢？ 硬防服务器中一般会配备入侵检测系统和预防系统&#x…...
2025盘古石杯决赛【手机取证】
前言 第三届盘古石杯国际电子数据取证大赛决赛 最后一题没有解出来，实在找不到，希望有大佬教一下我。 还有就会议时间，我感觉不是图片时间，因为在电脑看到是其他时间用老会议系统开的会。 手机取证 1、分析鸿蒙手机检材&#x…...
深度学习习题2
1.如果增加神经网络的宽度，精确度会增加到一个特定阈值后，便开始降低。造成这一现象的可能原因是什么？ A、即使增加卷积核的数量，只有少部分的核会被用作预测 B、当卷积核数量增加时，神经网络的预测能力会降低 C、当卷…...
#Uniapp篇：chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器：Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...
算法：模拟
1.替换所有的问号 1576. 替换所有的问号 - 力扣（LeetCode） 遍历字符串：通过外层循环逐一检查每个字符。遇到 ? 时处理： 内层循环遍历小写字母（a 到 z）。对每个字母检查是否满足： 与…...