《3D 数学基础》几何检测-最近点
目录
1. 直线上的最近点
2. 射线上的最近点
3. 点到平面的距离
4. 圆或球上的最近点
5. AABB上的最近点
1. 直线上的最近点
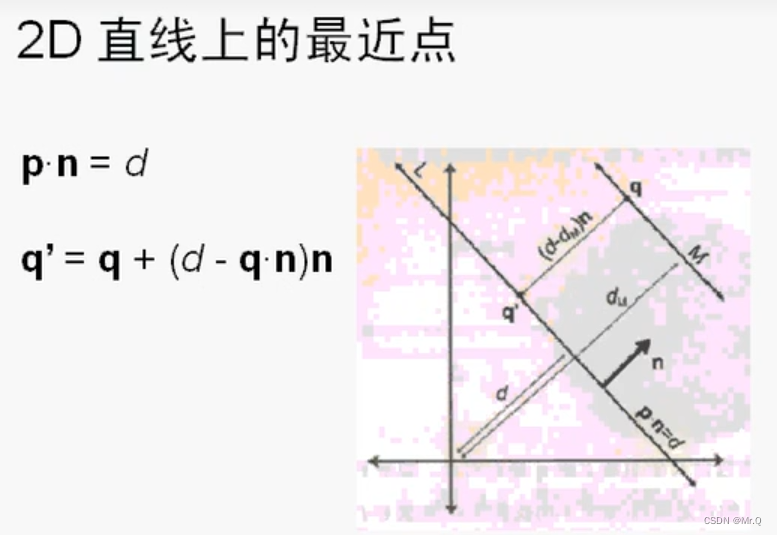
q'是距离q的最近点,也就是q在直线上的投影。
其中p是直线上的点(向量表示),n是直线的法向量(单位向量),d是直线到原点的距离。
2. 射线上的最近点

其中p_org是起始点,d是单位向量,t是自变量,可以无限大。
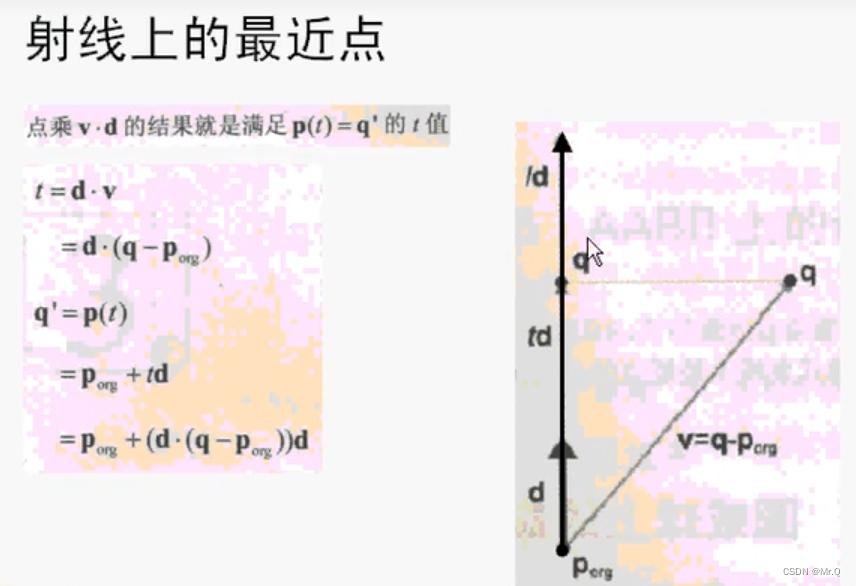
(1)先求自变量t, 点乘v·d结果就是t,因为v在d方向的投影就是点乘;
(2)带入公式p(t) = p_org + td即可求得q'=p_org + (d·(q-p_org))d。
3. 点到平面的距离
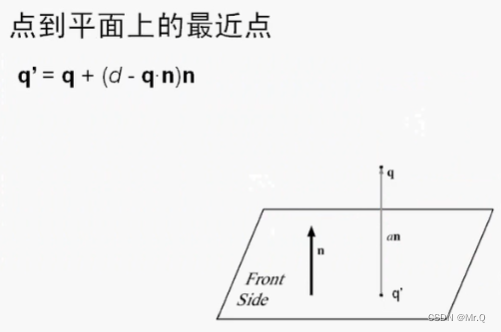
其中q是平面外的点,平面公式是q·n=d. p是平面上的点,n是法向量。
注意:和直线上的最近点公式是一样的。
4. 圆或球上的最近点
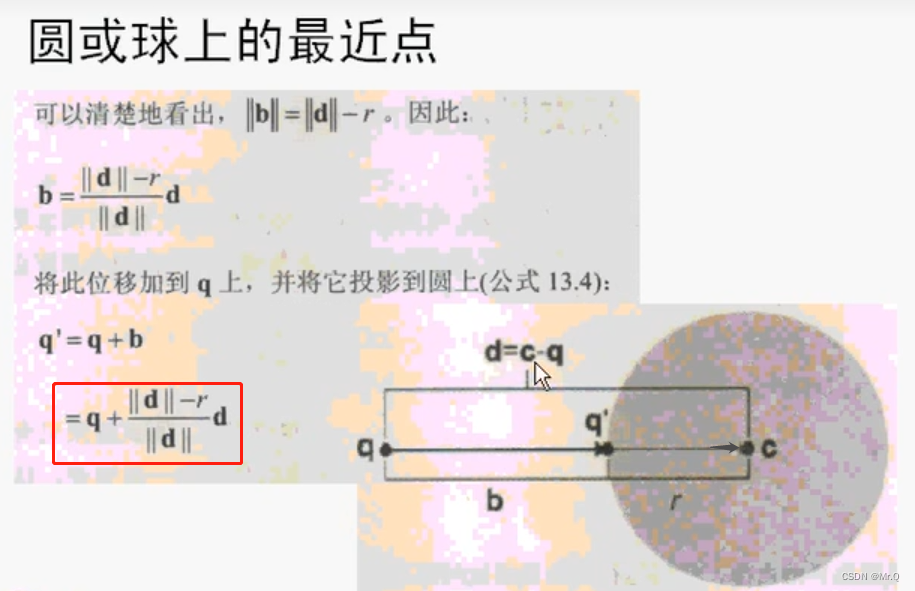
已知球心c和半径r,求q在球面的投影点q' 。d是c-q,其中加粗都是向量表示的点坐标。b是q到q'.
5. AABB上的最近点
AABB(Axis-Aligned Bounding Box,轴对齐的包围盒)是一个在三维空间中常用于表示物体边界的几何形状,通常由两个对角点(最小点和最大点)定义。要找到空间中的点到AABB上的最近点,可以使用以下方法:
-
检查点是否在AABB内部:
- 如果点在AABB内部,那么点本身就是AABB上的最近点。
-
检查点是否在AABB的某个坐标轴上的区间内:
- 对于每个坐标轴(x、y、z),检查点的坐标是否在AABB的最小坐标和最大坐标之间。如果是,那么点在该坐标轴上的投影就是AABB上的最近点。
-
否则,找到点到AABB上的最近点:
- 对于每个坐标轴,如果点的坐标小于AABB的最小坐标,则将点的坐标设置为AABB的最小坐标;如果点的坐标大于AABB的最大坐标,则将点的坐标设置为AABB的最大坐标。
- 现在,点的坐标就分别被截断到了AABB的各个坐标轴上的区间内,这就是AABB上的最近点。
import numpy as npdef closest_point_to_aabb(point, aabb_min, aabb_max):closest_point = np.copy(point)for i in range(len(point)):# Check if point coordinate is outside AABBif point[i] < aabb_min[i]:closest_point[i] = aabb_min[i]elif point[i] > aabb_max[i]:closest_point[i] = aabb_max[i]return closest_point# 示例用法
point = np.array([2, 3, 4]) #
# AABB
aabb_min = np.array([0, 0, 0])
aabb_max = np.array([5, 5, 5])closest = closest_point_to_aabb(point, aabb_min, aabb_max)
print("最近点:", closest)
待续。。。
参考:35.几何检测_哔哩哔哩_bilibili
相关文章:

《3D 数学基础》几何检测-最近点
目录 1. 直线上的最近点 2. 射线上的最近点 3. 点到平面的距离 4. 圆或球上的最近点 5. AABB上的最近点 1. 直线上的最近点 q是距离q的最近点,也就是q在直线上的投影。 其中p是直线上的点(向量表示),n是直线的法向量&#x…...

动态规划 -背包问题-详解
问题 注:大佬对此类问题的解法:动态规划背包问题总结 给你一个由 不同 整数组成的数组 nums ,和一个目标整数 target 。请你从 nums 中找出并返回总和为 target 的元素组合的个数。 题目数据保证答案符合 32 位整数范围。 示例 1ÿ…...
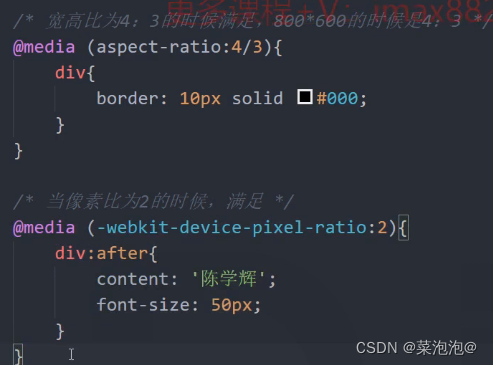
Bootstrap-- 媒体特性
最大、最小宽度例子: 横屏与竖屏例子: 宽度比与像素比例子:...

c# 用非递归的写法实现递归
最近写代码碰到了一个bug,就是递归次数太多爆堆栈了,然后就写了一个递归工具来解决这个问题。 using System; using System.Collections.Generic;/// <summary> /// 递归工具 /// </summary> public static class RecursionTool {//递归方式…...
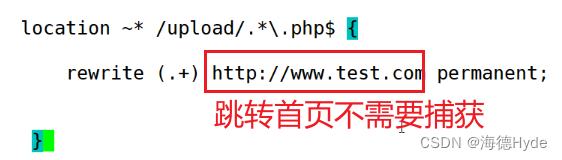
nginx之location的优先级和nginx的重定向
一、nginx之location的优先级和匹配方式(重点) (一)nginx的正则表达式 nginx的正则表达式 符号 含义 ^ 字符串的起始位置(以什么开头) $ 字符串的结束位置(以什么结尾) * 匹…...

【计算机网络】——前言计算机网络发展的历程概述
主页点击直达:个人主页 我的小仓库:代码仓库 C语言偷着笑:C语言专栏 数据结构挨打小记:初阶数据结构专栏 Linux被操作记:Linux专栏 LeetCode刷题掉发记:LeetCode刷题 算法:算法专栏 C头…...

eventfd
1. #include <sys/eventfd.h> int eventfd(unsigned int initval, int flags); //创建eventfd 参数含义: initval:创建eventfd时它所对应的64位计数器的初始值; flags:eventfd文件描述符的标志,可由三种选项组…...

BES耳机空间音频技术实现
BES耳机空间音频技术实现 是否需要申请加入数字音频系统研究开发交流答疑群(课题组)?加我微信hezkz17, 本群提供音频技术答疑服务 音响和耳机在空间音频技术上实现方式是不同的 虚拟现实可谓是空间音频技术最具代表性的应 用领域。虽然虚拟现实的起源可以追溯到1 9 6 8年, …...
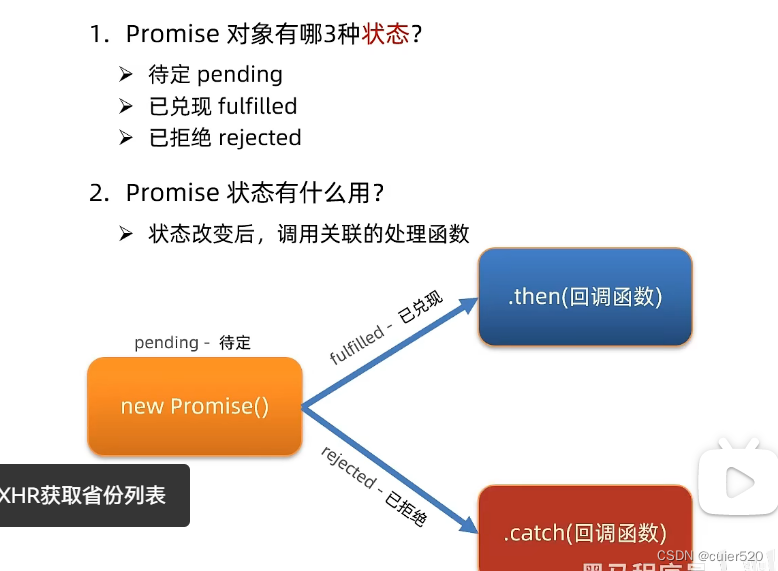
day27--AJAX(bootstrap之modal,toast;接口文档的一些用法;AJAX原理)
目录 Bootstrap之Modal: 显示和隐藏方法 通过自定义属性: 使用JS来控制弹框: Bootstrap之Toast: 接口文档一些用法: 删除图书: 图片上传: 图片上传步骤: 修改头像…...
:杂七杂八的记录)
【ArcGIS Pro二次开发】(70):杂七杂八的记录
本文用于记录一些使用频率较高但归类繁杂,非系统性的一些代码。 主要方便自己使用和查阅,随时更新。 1、从GDB数据库中打开【FeatureDataset\FeatureClass\Table】 using Geodatabase gdb new Geodatabase(new FileGeodatabaseConnectionPath(new Uri…...
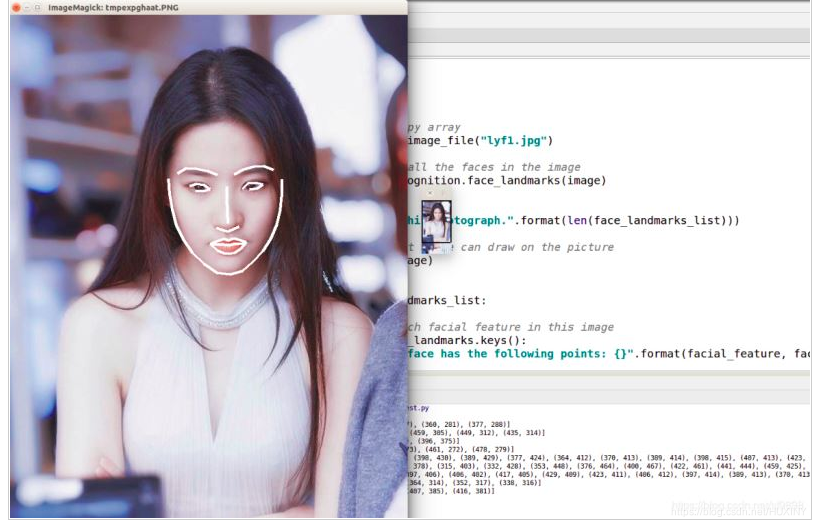
竞赛选题 深度学习 机器视觉 人脸识别系统 - opencv python
文章目录 0 前言1 机器学习-人脸识别过程人脸检测人脸对其人脸特征向量化人脸识别 2 深度学习-人脸识别过程人脸检测人脸识别Metric Larning 3 最后 0 前言 🔥 优质竞赛项目系列,今天要分享的是 🚩 深度学习 机器视觉 人脸识别系统 该项目…...
【工具】SSH端口转发管理器,专门管理SSH Port Forwarding
转载请注明出处:小锋学长生活大爆炸[xfxuezhang.cn] 开源代码看这里:http://xfxuezhang.cn/index.php/archives/1151/ 背景介绍 有时候需要用到ssh的端口转发功能。目前来说,要么是cmd里手敲指令,但每次敲也太麻烦了;或…...

opencv-phase 函数
计算梯度强度和方向 梯度的方向与边缘的方向总是垂直的。图像中的边缘可以指向各个方向,通常会取水平(左、右)、垂直(上、下)、对角线(左上、右上、左下、右下)等八个不同的方向计算梯度。 角度…...
44.ES
一、ES。 (1)es概念。 (1.1)什么是es。 (1.2)es的发展。 es是基于lucene写的。 (1.3)总结。 es是基于lucene写的。 (2)倒排索引。 (3…...

分权分域有啥内容?
目前的系统有什么问题? 现在我们的系统越来越庞大,可是每一个人进来的查看到的内容完全一样,没有办法灵活的根据不同用户展示不同的数据 例如我们有一个系统,期望不同权限的用户可以看到不同类型的页面,同一个页面不…...
6.Docker搭建RabbitMQ
1、端口开放 如果在云服务上部署需在安全组开通一下端口:15672、5672、25672、61613、1883。 15672(UI页面通信口)、5672(client端通信口)、25672(server间内部通信口)、61613(stomp 消息传输)、1883(MQTT消息队列遥测传输)。 2、安装镜像 docker pull rabbitmq 3、…...
用 docker 创建 jmeter 容器, 实现性能测试,该如何下手?
用 docker 创建 jmeter 容器, 实现性能测试 我们都知道,jmeter可以做接口测试,也可以用于性能测试,现在企业中性能测试也大多使用jmeter。docker是最近这些年流行起来的容器部署工具,可以创建一个容器,然后把项目放到…...

4年软件测试,突破不了20K,太卷了。。。
先说一个插曲:上个月我有同学在深圳被裁员了,和我一样都是软件测试,不过他是平安外包,所以整个组都撤了,他工资和我差不多都是14K。 现在IT互联网已经比较寒冬,特别是软件测试,裁员先裁测试&am…...
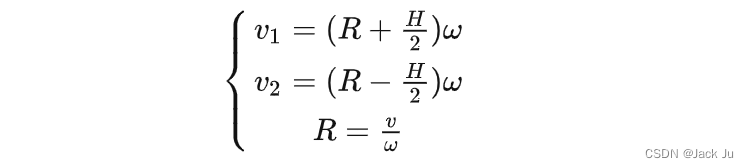
机器人控制算法——两轮差速驱动运动模型
1.Introduction 本文主要介绍针对于两轮差速模型的逆运动学数学推导。因为在机器人控制领域,决策规划控制层给执行器输出的控制指令v(车辆前进速度)和w(角速度),因此,我们比较关心,当底层两个驱动电机接收到此信息,如何…...

Queue简介
概念: 队列(Queue)是一种常见的线性数据结构,在Java中用于存储和操作元素序列。它基于先进先出(First-In-First-Out, FIFO)原则,即最早入队的元素首先出队。只能在队尾添加元素,在队…...

python如何将word的doc另存为docx
将 DOCX 文件另存为 DOCX 格式(Python 实现) 在 Python 中,你可以使用 python-docx 库来操作 Word 文档。不过需要注意的是,.doc 是旧的 Word 格式,而 .docx 是新的基于 XML 的格式。python-docx 只能处理 .docx 格式…...

DBAPI如何优雅的获取单条数据
API如何优雅的获取单条数据 案例一 对于查询类API,查询的是单条数据,比如根据主键ID查询用户信息,sql如下: select id, name, age from user where id #{id}API默认返回的数据格式是多条的,如下: {&qu…...

uniapp中使用aixos 报错
问题: 在uniapp中使用aixos,运行后报如下错误: AxiosError: There is no suitable adapter to dispatch the request since : - adapter xhr is not supported by the environment - adapter http is not available in the build 解决方案&…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

MacOS下Homebrew国内镜像加速指南(2025最新国内镜像加速)
macos brew国内镜像加速方法 brew install 加速formula.jws.json下载慢加速 🍺 最新版brew安装慢到怀疑人生?别怕,教你轻松起飞! 最近Homebrew更新至最新版,每次执行 brew 命令时都会自动从官方地址 https://formulae.…...
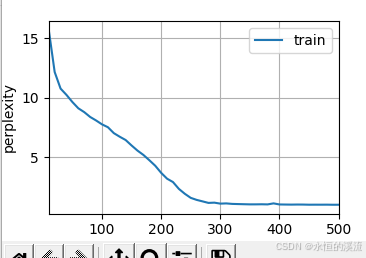
李沐--动手学深度学习--GRU
1.GRU从零开始实现 #9.1.2GRU从零开始实现 import torch from torch import nn from d2l import torch as d2l#首先读取 8.5节中使用的时间机器数据集 batch_size,num_steps 32,35 train_iter,vocab d2l.load_data_time_machine(batch_size,num_steps) #初始化模型参数 def …...

GeoServer发布PostgreSQL图层后WFS查询无主键字段
在使用 GeoServer(版本 2.22.2) 发布 PostgreSQL(PostGIS)中的表为地图服务时,常常会遇到一个小问题: WFS 查询中,主键字段(如 id)莫名其妙地消失了! 即使你在…...
C++中vector类型的介绍和使用
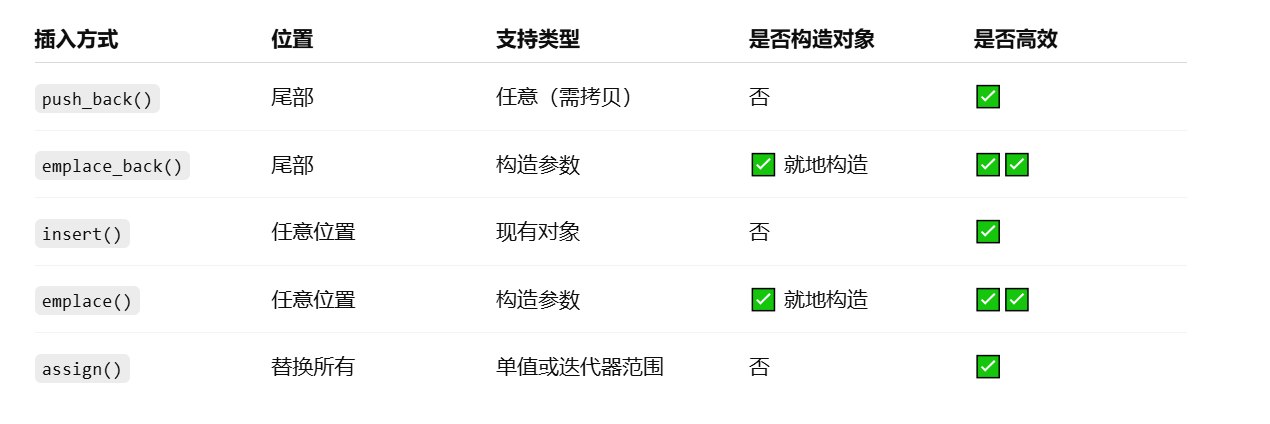
文章目录 一、vector 类型的简介1.1 基本介绍1.2 常见用法示例1.3 常见成员函数简表 二、vector 数据的插入2.1 push_back() —— 在尾部插入一个元素2.2 emplace_back() —— 在尾部“就地”构造对象2.3 insert() —— 在任意位置插入一个或多个元素2.4 emplace() —— 在任意…...

2025 后端自学UNIAPP【项目实战:旅游项目】7、景点详情页面【完结】
1、获取景点详情的请求【my_api.js】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http(/login/getWXSessionKey, {code,avatar}); };//…...

在Android13上添加系统服务的好用例子
在Android13上添加一个自动的system service例子 留好,备用。 --- .../prebuilts/api/30.0/plat_pub_versioned.cil | 76 - .../prebuilts/api/31.0/plat_pub_versioned.cil | 94 - .../prebuilts/api/32.0/plat_pub_versioned.cil | 94 - frameworks/base/co…...
