详细介绍数据结构-堆
计算机中的堆数据结构
什么是堆
在计算机科学中,堆(Heap)是一种重要的数据结构,它用于在动态分配时存储和组织数据。堆是一块连续的内存区域,其中每个存储单元(通常是字节)都与另一个存储单元紧密相邻。
堆和栈是计算机内存的两种主要部分。其中,栈用于存储局部变量和函数调用的信息,而堆则用于存储动态分配的变量和数据结构。
堆的特点是可以动态地增加和减少内存,而且可以任意分配内存的大小。这意味着你可以在运行时分配内存,以存储例如动态数组,图形数据结构,优先级队列等数据。
堆的好处及适用场景
堆数据结构有许多优点,这使得它在许多计算场景中都非常有用。
- 动态内存分配:堆允许我们在运行时动态地分配和释放内存。这意味着我们可以在程序执行的过程中,根据需要创建或删除数据。
- 大小不定:与栈不同,堆的大小不是预先确定的。这意味着我们可以用它来存储大量的数据,只要可用的系统内存允许。
- 支持自定义数据类型:由于堆是通用的内存分配机制,因此可以用它来存储任何类型的数据,不仅仅是基本类型。
下面是一些适用的场景:
- 动态数组:堆是创建动态数组(例如动态调整大小的数组)的理想场所。你可以在运行时根据需要增加或减少数组的大小。
- 优先级队列:优先级队列经常使用堆来实现。在这种情况下,堆的特性允许我们有效地插入和删除元素,以及在O(1)时间内查找最大(或最小)元素。
- 动态链接列表:在动态链接列表中,我们需要在运行时创建和删除节点。这也需要使用堆内存。
- 图形和树结构:图形和树结构通常使用堆来实现,因为这些数据结构需要在运行时动态地添加和删除节点。
C++代码实现一个堆并测试
以下是一个简单的最小堆的C++实现。注意这个例子只是为了教育目的,并没有包含一些关键的功能,比如防止溢出或检查是否溢出。
然后,我们可以继续实现其他堆操作,例如删除元素,查找最小元素等。以下是一个更完整的堆实现,包括上述缺失的操作:
#include <iostream>
#include <vector>
#include <stdexcept> // for std::out_of_range class MinHeap {
private: std::vector<int> data; // underlying data structure int parent(int i) { return (i - 1) / 2; } // parent index int leftChild(int i) { return 2 * i + 1; } // left child index int rightChild(int i) { return 2 * i + 2; } // right child index void siftUp(int i) { // sift element i up to its proper place while (i > 0 && data[parent(i)] > data[i]) { std::swap(data[parent(i)], data[i]); i = parent(i); } } void siftDown(int i) { // sift element i down to its proper place int minIndex = i; // index of current minimum element int l = leftChild(i); // left child index if (l < data.size() && data[l] < data[minIndex]) { minIndex = l; } int r = rightChild(i); // right child index if (r < data.size() && data[r] < data[minIndex]) { minIndex = r; } if (i != minIndex) { // swap i and minIndex if necessary and repeat siftDown on affected subtree std::swap(data[i], data[minIndex]); siftDown(minIndex); } } void siftUpForInsert(int i) { // sift element i up to its proper place after insert for heap property to be maintained while (i > 0 && data[parent(i)] > data[i]) { std::swap(data[parent(i)], data[i]); i = parent(i); } } public: void insert(int value) { // insert value into heap and maintain heap order property data.push_back(value); // append value to the end of the vector and remember its index (size - 1) siftUpForInsert(data.size() - 1); // sift up to maintain heap order property (parent is larger than its children) after insert } int extractMin() { // extract the current minimum element from heap and maintain heap order property if (data.empty()) { throw std::out_of_range("Heap is empty"); } // heap is empty, so there is no min element throw an exception here to indicate that the situation cannot be handled and the program should stop execution with an error message to user indicating the error situation that occurred here. int minElement = data[0]; // store the minimum element in a temporary variable minElement before swapping it with the last element in the vector and deleting it from the vector in the next step (data.pop_back()) as this will change the size of the vector and all further indices will shift downwards by one position in memory. std::swap(data[0], data[data.size() - 1]); // swap the first element with the last element in the vector as they will have swapped roles after this step (the last element will become the new first element/minimum element in its new position in memory while the first element will become the last element in its new position in memory after this swap operation) for maintaining the heap property after extract operation. data.pop_back(); // remove the last element from the vector as it has just become unnecessary/redundant/no longer required in memory after the previous swapping step to maintain heap order property as required. As it is removed, all further indices will shift downwards by one position in memory for maintaining the heap property after extract operation. siftDown(0); // sift down the new first element/minimum element to maintain heap order property after extract operation as required. The root/first element is always at index 0 in a heap as shown in all figures above for heap data structure shown above in this code segment also. Heap is a complete binary tree (each node has either two children or no children). Binary tree is a type of tree where each node has}
相关文章:

详细介绍数据结构-堆
计算机中的堆数据结构 什么是堆 在计算机科学中,堆(Heap)是一种重要的数据结构,它用于在动态分配时存储和组织数据。堆是一块连续的内存区域,其中每个存储单元(通常是字节)都与另一个存储单元…...
001flutter基础学习
flutter基础学习 参考:https://book.flutterchina.club/chapter1/flutter_intro.html Flutter是谷歌的移动UI框架跨平台: Linux,Android, IOS,Fuchsia原生用户界面:它是原生的,让我们体验更好,性能更好开源免费:完全开源,可以进行商用Flutter与主流框架的对比 Cor…...

leetCode 1143.最长公共子序列 动态规划 + 图解
此题我的往期文章推荐: leetCode 1143.最长公共子序列 动态规划 滚动数组-CSDN博客https://blog.csdn.net/weixin_41987016/article/details/133689692?spm1001.2014.3001.5501leetCode 1143.最长公共子序列 一步步思考动态规划 优化空间复杂度_呵呵哒(…...

解密人工智能:KNN | K-均值 | 降维算法 | 梯度Boosting算法 | AdaBoosting算法
文章目录 一、机器学习算法简介1.1 机器学习算法包含的两个步骤1.2 机器学习算法的分类 二、KNN三、K-均值四、降维算法五、梯度Boosting算法和AdaBoosting算法六、结语 一、机器学习算法简介 机器学习算法是一种基于数据和经验的算法,通过对大量数据的学习和分析&…...
Python深度学习实践
线性模型 课程 import numpy as np import matplotlib.pyplot as plt x_data[1.0,2.0,3.0] y_data[2.0,4.0,6.0] #前馈函数 def forward(x):return x*w #损失函数 def loss(x,y):y_predforward(x)return (y_pred-y)*(y_pred-y) w_list[] mse_list[] for w in np.arange(0.0,4…...
VS2017+QT+PCL环境配置
前言: 最近自己再弄一下小项目中需要用到pcl来开发点云的显示,但是却遇到很多坑,所以记录下来分析给知音人。 避雷:由于vtk和pcl之间有版本以来关系,但是安装过程是不变的。 选择对应的版本参考如下安装: pcl1.8.1依赖vtk版本7.1.1;pcl1.9.1至pcl1.12.0依赖vtk最低版本为…...
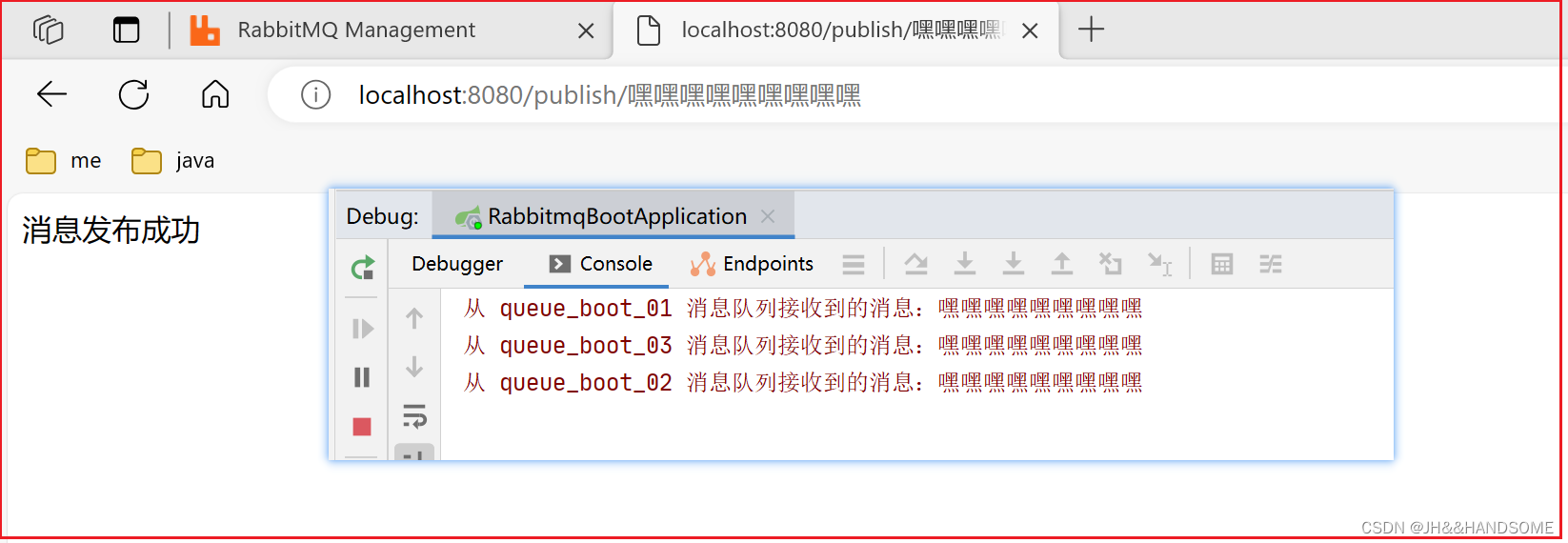
207、SpringBoot 整合 RabbitMQ 实现消息的发送 与 接收(监听器)
目录 ★ 发送消息★ 创建队列的两种方式代码演示需求1:发送消息1、ContentUtil 先定义常量2、RabbitMQConfig 创建队列的两种方式之一:配置式:问题: 3、MessageService 编写逻辑PublishController 控制器application.properties 配…...
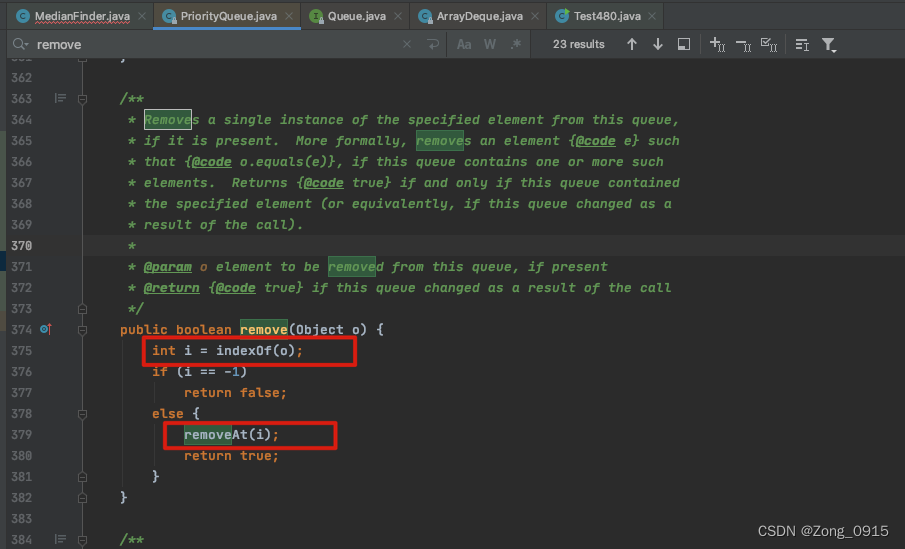
想要精通算法和SQL的成长之路 - 滑动窗口和大小根堆
想要精通算法和SQL的成长之路 - 滑动窗口和大小根堆 前言一. 大小根堆二. 数据流的中位数1.1 初始化1.2 插入操作1.3 完整代码 三. 滑动窗口中位数3.1 在第一题的基础上改造3.2 栈的remove操作 前言 想要精通算法和SQL的成长之路 - 系列导航 一. 大小根堆 先来说下大小根堆是什…...
Python算法练习 10.15
leetcode 2130 链表的最大孪生和 在一个大小为 n 且 n 为 偶数 的链表中,对于 0 < i < (n / 2) - 1 的 i ,第 i 个节点(下标从 0 开始)的孪生节点为第 (n-1-i) 个节点 。 比方说,n 4 那么节点 0 是节点 3 的孪…...

智能防眩目前照灯系统控制器ADB
经纬恒润的自适应远光系统—— ADB(Adaptive Driving Beam) 是一种能够根据路况自适应变换远光光型的智能远光控制系统。根据本车行驶状态、环境状态以及道路车辆状态,ADB 系统自动为驾驶员开启或退出远光。同时,根据车辆前方视野…...
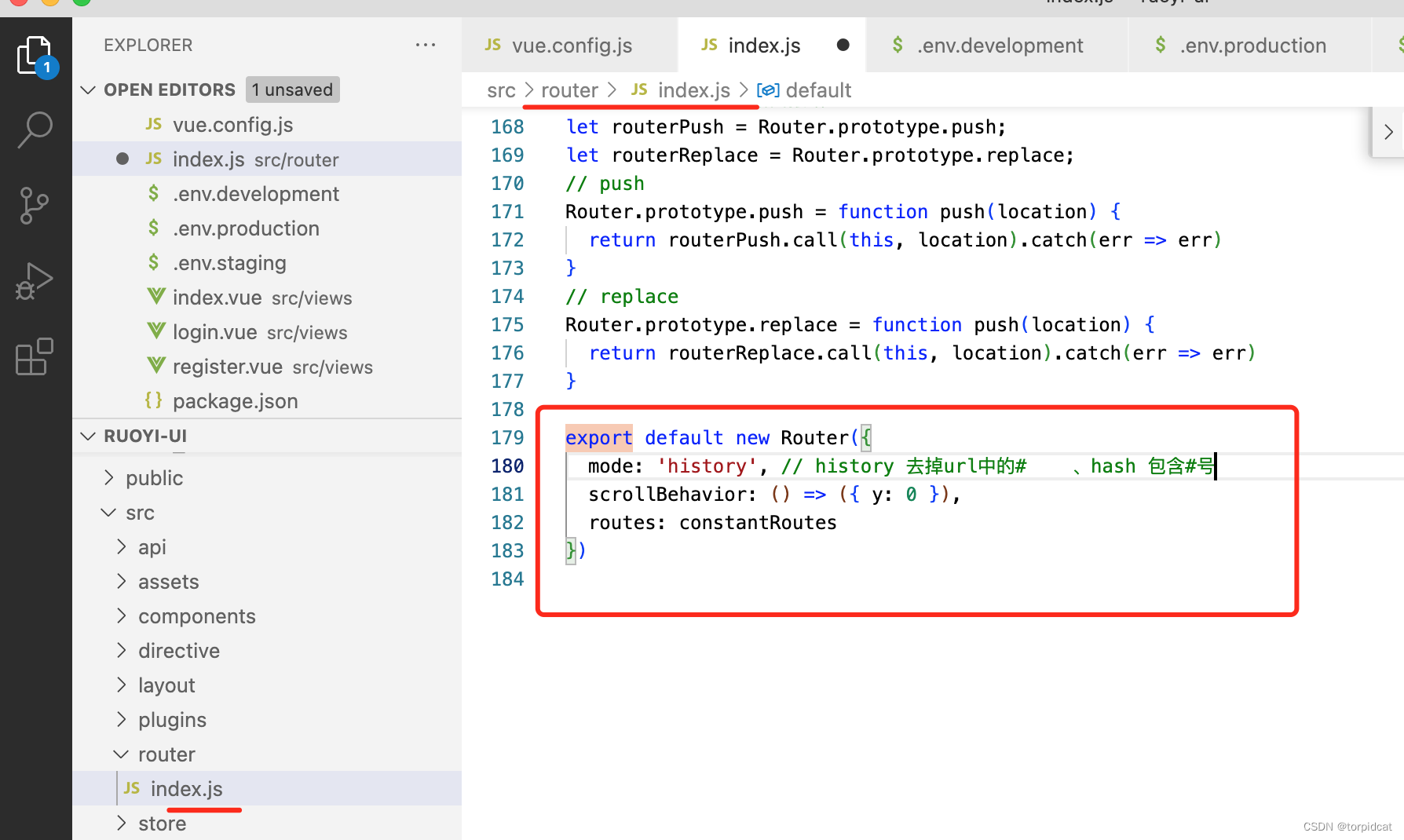
若依 ruoyi 路径 地址 # 井号去除
export default new Router({mode: history, // history 去掉url中的# 、hash 包含#号scrollBehavior: () > ({ y: 0 }),routes: constantRoutes })...
Elasticsearch 和 Arduino:一起变得更好!
作者:Enrico Zimuel 使用 Arduino IoT 设备与 Elasticsearch 和 Elastic Cloud 进行通信的简单方法 在 Elastic,我们不断寻找简化搜索体验的新方法,并开始关注物联网世界。 来自物联网的数据收集可能非常具有挑战性,尤其是当我们…...

基于Ubuntu环境Git 服务器搭建及使用
多人合作开发的时候 常常会需要使用代码管理平台,保持代码一致和解决冲突。在工作中我使用过SVN和TFS,本文说明另外一种平台,Git,下面是基于Ubuntu环境安装并简单使用Git服务器。 确认安装git apt install git levilevi-ThinkPa…...
【quartus13.1/Verilog】swjtu西南交大:计组课程设计
实验目的: 通过学习简单的指令系统及其各指令的操作流程,用 Verilog HDL 语言实 现简单的处理器模块,并通过调用存储器模块,将处理器模块和存储器模块连接形成简 化的计算机核心部件组成的系统。 二. 实验内容 1. 底层用 Verilog…...

基于springboot的网上点餐系统论文开题报告
一、选题背景 随着互联网和移动互联网技术的快速发展,网上点餐成为了人们越来越喜欢的一种点餐方式。一些具有创新意识的餐厅也开始逐渐尝试利用互联网技术来提升用户的点餐体验。因此,开发一个基于Spring Boot的网上点餐系统就显得非常必要和重要。 二…...
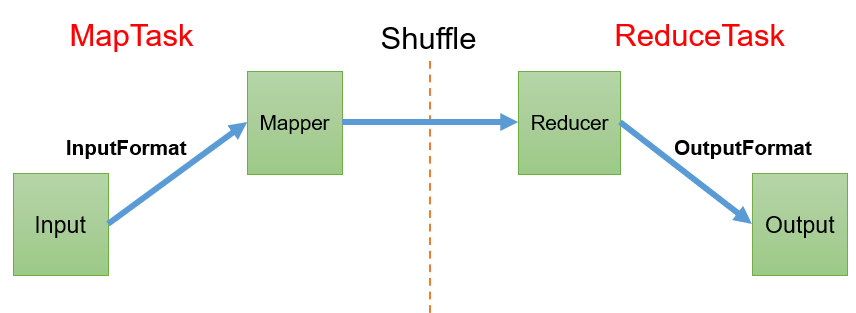
Hadoop3教程(九):MapReduce框架原理概述
文章目录 简介参考文献 简介 这属于整个MR中最核心的一块,后续小节会展开描述。 整个MR处理流程,是分为Map阶段和Reduce阶段。 一般,我们称Map阶段的进程是MapTask,称Reduce阶段是ReduceTask。 其完整的工作流程如图ÿ…...

使用PyTorch加载数据集:简单指南
💗💗💗欢迎来到我的博客,你将找到有关如何使用技术解决问题的文章,也会找到某个技术的学习路线。无论你是何种职业,我都希望我的博客对你有所帮助。最后不要忘记订阅我的博客以获取最新文章,也欢…...
)
【考研数学】线性代数第六章 —— 二次型(2,基本定理及二次型标准化方法)
文章目录 引言一、二次型的基本概念及其标准型1.2 基本定理1.3 二次型标准化方法1. 配方法2. 正交变换法 写在最后 引言 了解了关于二次型的基本概念以及梳理了矩阵三大关系后,我们继续往后学习二次型的内容。 一、二次型的基本概念及其标准型 1.2 基本定理 定理…...
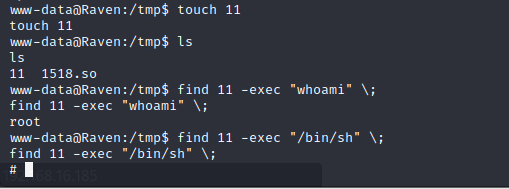
Raven2靶机渗透
1. 信息收集 1.1 主机探测 sudo arp-scan -l1.2 端口扫描 nmap -p- -A 192.168.16.185开放了80端口,尝试登录网址查看信息,通过浏览器插件找出指纹 1.3 目录扫描 访问登录界面,发现remember Me怀疑是shiro界面 登录/vendor/界面࿰…...

UE5中双pass解决半透明材质乱序问题
透明度材质乱序问题一直是半透明效果时遇到的比较多的问题,用多pass方案只能说一定程度上解决,当遇到多半透明物体穿插等情况时,仍然不能完美解决。 双pass方案Unity用的比较多,因为Unity支持多个pass绘制。在UE中我们可以以复制多…...

XML Group端口详解
在XML数据映射过程中,经常需要对数据进行分组聚合操作。例如,当处理包含多个物料明细的XML文件时,可能需要将相同物料号的明细归为一组,或对相同物料号的数量进行求和计算。传统实现方式通常需要编写脚本代码,增加了开…...

变量 varablie 声明- Rust 变量 let mut 声明与 C/C++ 变量声明对比分析
一、变量声明设计:let 与 mut 的哲学解析 Rust 采用 let 声明变量并通过 mut 显式标记可变性,这种设计体现了语言的核心哲学。以下是深度解析: 1.1 设计理念剖析 安全优先原则:默认不可变强制开发者明确声明意图 let x 5; …...

ES6从入门到精通:前言
ES6简介 ES6(ECMAScript 2015)是JavaScript语言的重大更新,引入了许多新特性,包括语法糖、新数据类型、模块化支持等,显著提升了开发效率和代码可维护性。 核心知识点概览 变量声明 let 和 const 取代 var…...

DeepSeek 赋能智慧能源:微电网优化调度的智能革新路径
目录 一、智慧能源微电网优化调度概述1.1 智慧能源微电网概念1.2 优化调度的重要性1.3 目前面临的挑战 二、DeepSeek 技术探秘2.1 DeepSeek 技术原理2.2 DeepSeek 独特优势2.3 DeepSeek 在 AI 领域地位 三、DeepSeek 在微电网优化调度中的应用剖析3.1 数据处理与分析3.2 预测与…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

页面渲染流程与性能优化
页面渲染流程与性能优化详解(完整版) 一、现代浏览器渲染流程(详细说明) 1. 构建DOM树 浏览器接收到HTML文档后,会逐步解析并构建DOM(Document Object Model)树。具体过程如下: (…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

12.找到字符串中所有字母异位词
🧠 题目解析 题目描述: 给定两个字符串 s 和 p,找出 s 中所有 p 的字母异位词的起始索引。 返回的答案以数组形式表示。 字母异位词定义: 若两个字符串包含的字符种类和出现次数完全相同,顺序无所谓,则互为…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...
