atcoder [Road of the King] 题解(DP好题)
题面
简要题意:有一个 n n n 个点的图,目前一条边都没有。有一个人在 1 1 1 号点要进行 m m m 次移动, 终点不必是 1 1 1 号点。加入第 i i i 次的从 u u u 移动到了 v v v, 那么 u u u 到 v v v 之间出现一条有向边。问一共有多少序列满足最后 n n n 个点组成的图 是一个强联通图。答案对 1 0 9 + 7 10^9 + 7 109+7 取模。 1 ≤ n , m ≤ 300 1 \leq n,m \leq 300 1≤n,m≤300。
分析:
注意到一个性质,就是如果要形成强联通图,那么所有的点都要和 1 1 1 能够相互到达。因为是从 1 1 1 出发,所以序列里所有的点 1 1 1 都可以到达,只要这 n n n 个点都能到达 1 1 1 ,那么这 n n n 个点组成的图就一定是一个强联通图。 我们根据这条性质来划分状态。
设 d p i , j , k dp_{i, j, k} dpi,j,k 表示当前已经走了 i i i 步,涉及到的点有 j j j 个, 跟 1 1 1 形成强联通的点有 k k k 个。注意当前点可以看做是没有跟 1 1 1 形成强联通的点。我们考虑转移:
如果下一步走到了一个没有跟 1 1 1 形成强联通但是已经设计的点,那么有 ( j − k ) × d p i , j , k → d p i + 1 , j , k (j - k) \times dp_{i,j, k} \rightarrow dp_{i+1, j, k} (j−k)×dpi,j,k→dpi+1,j,k。
如果下一步走到了一个跟 1 1 1 形成强联通的点,那么所有涉及到的点都会和 1 1 1 形成强联通,有 k × d p i , j , k → d p i + 1 , j , j k \times dp_{i, j, k} \rightarrow dp_{i+1, j, j} k×dpi,j,k→dpi+1,j,j。
如果下一步走到了一个还未涉及到的点,那么有 ( n − j ) × d p i , j , k → d p i + 1 , j + 1 , k (n-j) \times dp_{i,j, k} \rightarrow dp_{i+1,j+1,k} (n−j)×dpi,j,k→dpi+1,j+1,k。
最后输出 d p m , n , n dp_{m,n,n} dpm,n,n 就好了。
#include<bits/stdc++.h>
#define N 310
#define LL long long
#define mod 1000000007
using namespace std;
int n, m;
LL dp[N][N][N];// dp[i][j][k] 表示走了i步,已经拓展了j个点, 能与1形成强联通的点数为k 的方案数
int main(){cin >> n >> m;dp[0][1][1] = 1LL;for(int i = 0; i <= m; i++){for(int j = 1; j <= n; j++){for(int k = 1; k <= j; k++){dp[i + 1][j + 1][k] = (dp[i + 1][j + 1][k] + dp[i][j][k] * (1LL * (n - j))) % mod;dp[i + 1][j][k] = (dp[i + 1][j][k] + dp[i][j][k] * (1LL * (j - k))) % mod;dp[i + 1][j][j] = (dp[i + 1][j][j] + dp[i][j][k] * (1LL * k)) % mod;}}}cout << dp[m][n][n] << endl;return 0;
}
相关文章:
)
atcoder [Road of the King] 题解(DP好题)
题面 简要题意:有一个 n n n 个点的图,目前一条边都没有。有一个人在 1 1 1 号点要进行 m m m 次移动, 终点不必是 1 1 1 号点。加入第 i i i 次的从 u u u 移动到了 v v v, 那么 u u u 到 v v v 之间出现一条有向边。问…...

CImageList 图像列表
一、CImageList类Create函数参数解析 BOOL Create(int cx,int cy,UINT nFlags,int nInitial,int nGrow ); 1.1) cx,cy:图片的实际像素宽与高; nFlags:创建图像列表的类型,包括4/8/16/24/32/位色; nFlags确定建立图…...

【OpenGL】四、坐标系统和摄像机
坐标转换 文章目录 坐标转换坐标系统的转换局部空间(Local Space)->世界空间(World Space)世界空间(World Space)->观察空间(View Space/View Space)裁剪空间(Clip Space)MVP矩阵 坐标系统的转换 了解坐标系统和空间变换之前需要先了解…...
使用vcpkg管理依赖第三库
文章目录 使用vcpkg管理依赖第三库vcpkg安装vcpkg经典模式使用从仓库列表搜索依赖项从某个基线版本的列表中查询某个依赖项信息安装依赖库 vcpkg清单模式的使用vcpkg清单模式的使用例子说明 使用vcpkg管理依赖第三库 vcpkg 有两种操作模式:经典模式和清单模式。 在…...

Android渲染一个列表的过程,并提供动态改变样式
1、index.xml 布局文件,我省略了其他代码,我们需要recyclerview保证在规定范围内,如果列表元素过多可以滑动 <LinearLayoutandroid:layout_width"match_parent"android:layout_height"match_parent"android:layout_…...
Leetcode—260.只出现一次的数字III【中等】
2023每日刷题(三) Leetcode—260.只出现一次的数字III 借助lowbit的解题思想 参考的灵茶山艾府大神的题解 实现代码 /*** Note: The returned array must be malloced, assume caller calls free().*/ int* singleNumber(int* nums, int numsSize, in…...
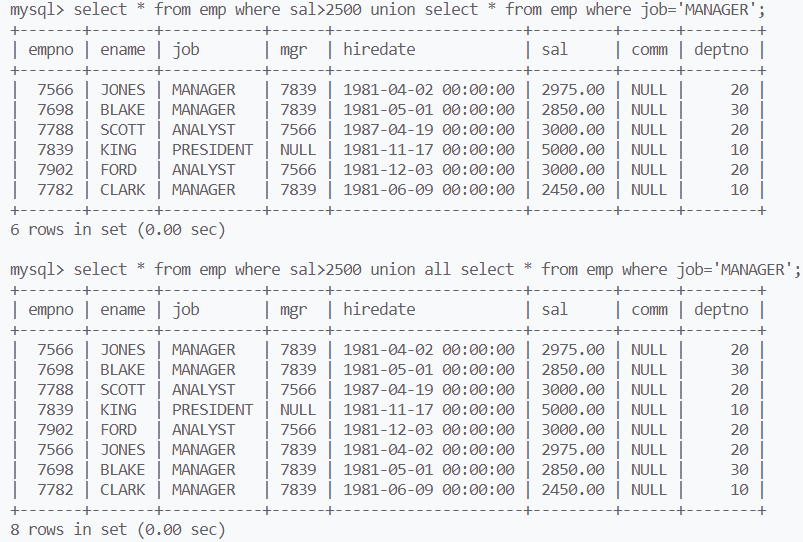
Mysql 约束,基本查询,复合查询与函数
文章目录 约束空属性约束默认值约束zerofill主键约束自增长约束唯一键约束外键约束 查询select的执行顺序单表查询排序 updatedelete整张表的拷贝复合语句group by分组查询 函数日期函数字符串函数数学函数其他函数 复合查询合并查询union 约束 空属性约束 两个值:…...

web前端基础CSS------美化页面“footer”部分
一,实验代码 <!DOCTYPE html> <html><head><meta charset"utf-8"><title>关于我们</title><style type"text/css">#footer{margin: 10px 0px;background: #f5f5f5;border: top 1px solid #eee ;}#f…...

在中国,技术到底有多有用?
🙌秋名山码民的主页 😂oi退役选手,Java、大数据、单片机、IoT均有所涉猎,热爱技术,技术无罪 🎉欢迎关注🔎点赞👍收藏⭐️留言📝 获取源码,添加WX 目录 前言1.…...

《动手学深度学习 Pytorch版》 9.2 长短期记忆网络(LSTM)
解决隐变量模型长期信息保存和短期输入缺失问题的最早方法之一是长短期存储器(long short-term memory,LSTM)。它与门控循环单元有许多一样的属性。长短期记忆网络的设计比门控循环单元稍微复杂一些,却比门控循环单元早诞生了近 2…...
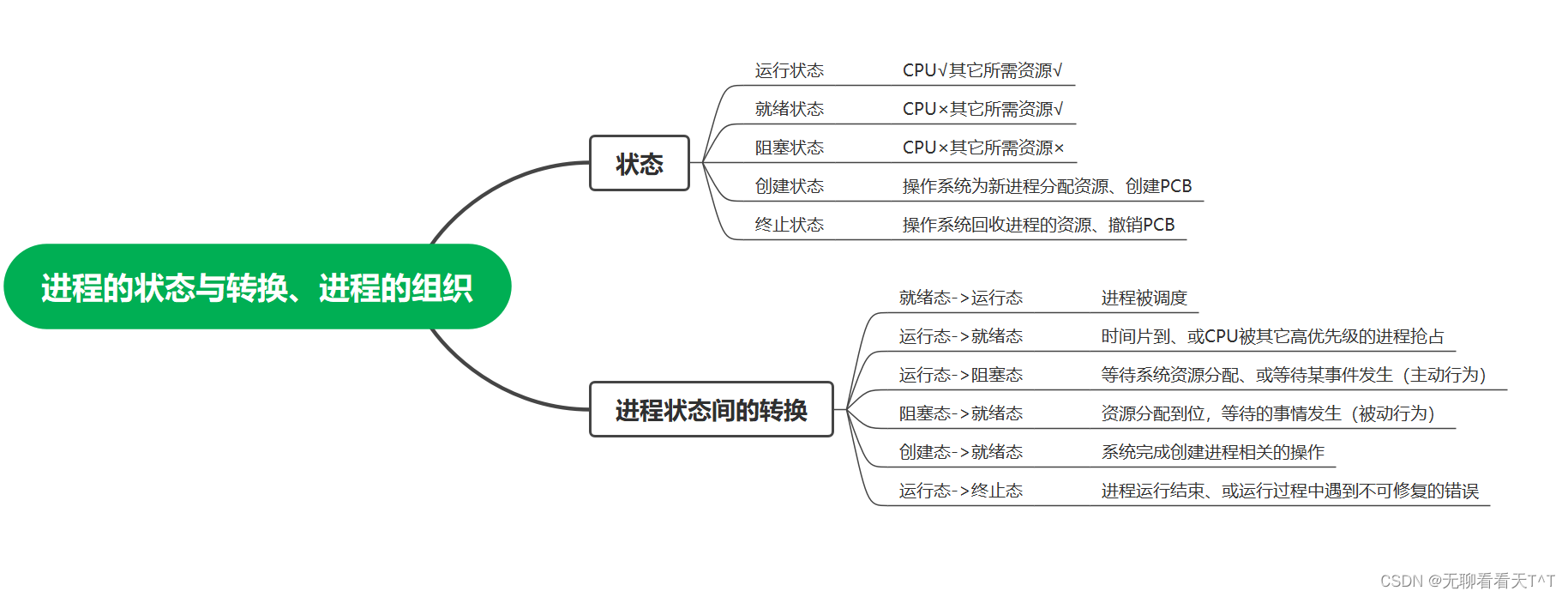
计算机操作系统-第十一天
目录 1、进程的状态 创建态与就绪态 运行态 终止态 新建态 结束态 进程状态的转换 进程的组织方式 链接方式(常见) 索引方式(少见) 本节思维导图 1、进程的状态 创建态与就绪态 1、进程正在被创建时,处于…...
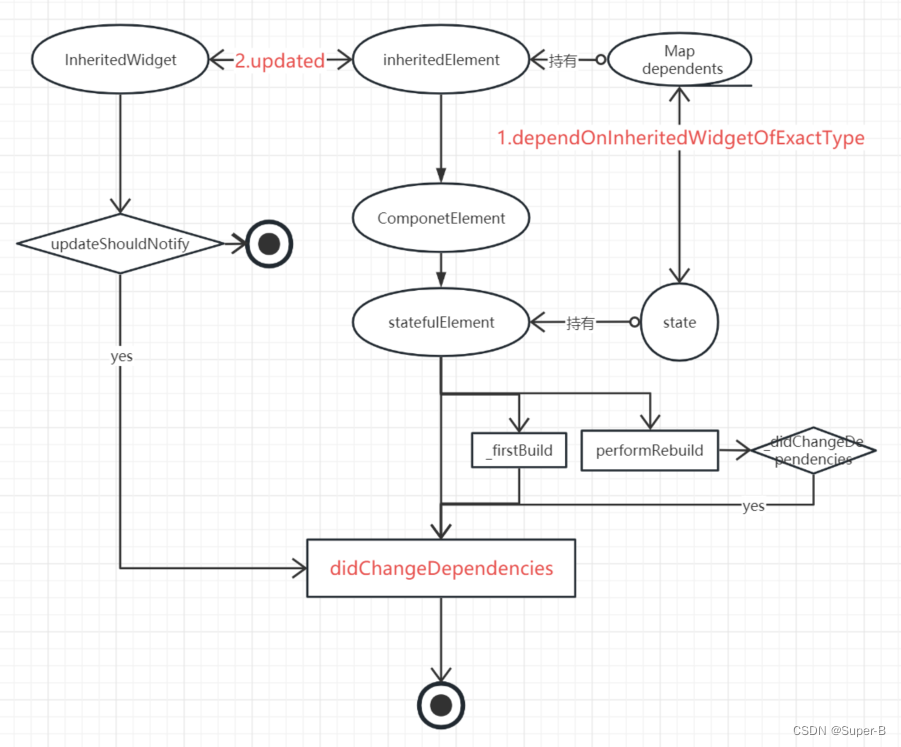
Flutter视图原理之StatefulWidget,InheritedWidget
目录 StatefulElement1. 构造函数2. build3. _firstBuild3. didChangeDependencies4. setState InheritedElement1. Element类2. _updateInheritance3. InheritedWidget数据向下传递3.1 dependOnInheritedWidgetOfExactType 4. InheritedWidget的状态绑定4.1. ProxyElement 在f…...

观察者模式-对象间的联动
有个商城小程序,用户希望当有新品上市的时候能通知他们。这样用户就可以不要时刻盯着小程序了。在这个场景中,用户向小程序订阅了一个服务——发送新品短信。小程序在有新品上线时负责向订阅客户发出这个消息。 这就是发布-订阅模式,也称观察…...
Webpack十大缺点:当过度工程化遇上简单的静态页面
🤍 前端开发工程师(主业)、技术博主(副业)、已过CET6 🍨 阿珊和她的猫_CSDN个人主页 🕠 牛客高级专题作者、在牛客打造高质量专栏《前端面试必备》 🍚 蓝桥云课签约作者、已在蓝桥云…...
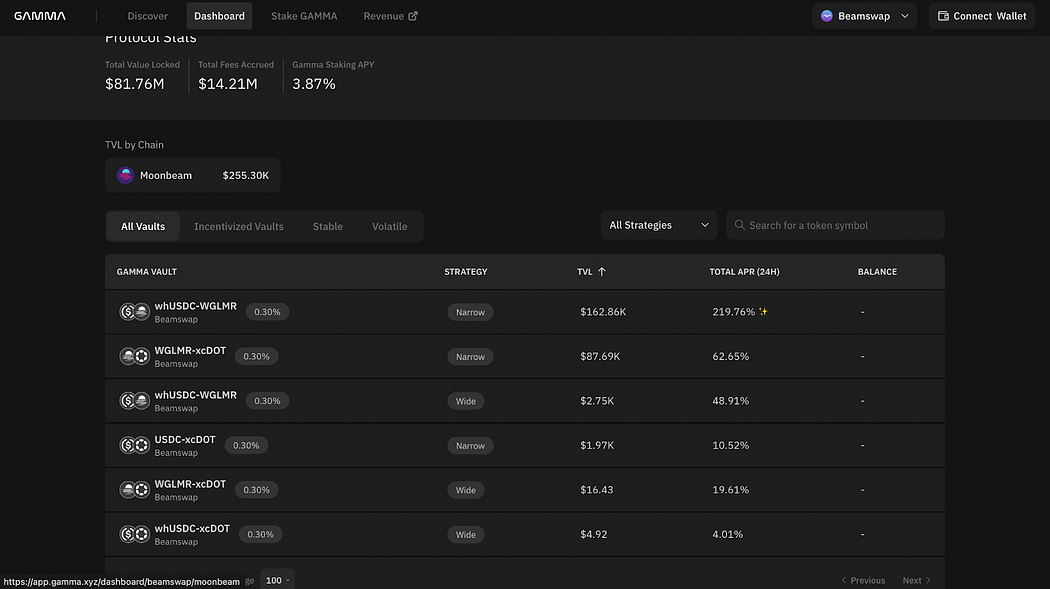
新手指南|如何快速参与Moonbeam Ignite
Moonbeam Ignite是社区熟悉的有奖链上交互活动,将有300万枚GLMR作为生态激励注入Moonbeam生态系统,体验MoonbeamMoonbeam生态的应用即可获取相应Token奖励。Beamex/Beamswap、Moonwell和Gamma作为首批参与Moonbeam Ignite的三家项目方,将在活…...

VR航天科普主题公园模拟太空舱体验馆vr航天模拟体验设备
VR航天航空体验馆巡展是一项非常受欢迎的展览活动,可以让公众在现场体验到航天飞行的乐趣。 普乐蛙VR展览组织者会设计一个航天航空主题的VR体验馆,并在馆内设置各种航天航空相关的展示内容,如太空舱、火箭发射、星际航行等。 其次࿰…...

Spring Boot OAuth 2.0整合详解
目录 一、Spring Boot 2.x 示例 1、初始化设置 2、设置重定向URI 3、配置 application.yml 4、启动应用程序 二、Spring Boot 2.x 属性映射 二、CommonOAuth2Provider 三、配置自定义提供者(Provider)属性 四、覆盖 Spring Boot 2.x 的自动配置…...
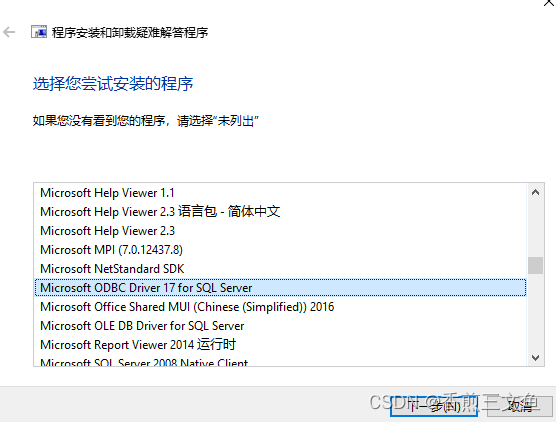
安装visual studio报错“无法安装msodbcsql“
在安装visual studio2022时安装完成后提示无法安装msodbcsql, 查看日志文件详细信息提示:指定账户已存在。 未能安装包“msodbcsql,version17.2.30929.1,chipx64,languagezh-CN”。 搜索 URL https://aka.ms/VSSetupErrorReports?qPackageIdmsodbcsql;PackageActi…...

webGL编程指南 第三章 矩阵平移三角形.translatedTriangle_Matrix
我会持续更新关于wegl的编程指南中的代码。 当前的代码不会使用书中的缩写,每一步都是会展开写。希望能给后来学习的一些帮助 git代码地址 :git 接着 上一节 中 我们使用矩阵进行旋转,这次我们使用矩阵实现位移 <!DOCTYPE html> <…...
修改echarts的tooltip样式 折线图如何配置阴影并实现渐变色和自适应
图片展示 一、引入echarts 这里不用多解释 vue里使用 import echarts from “echarts”; html页面引用js文件或用script标签引用 二、定义一个具有宽高的dom div <div id"echart-broken" style"width:400px;height: 200px;"></div>三、定义…...
Cesium相机控制)
三维GIS开发cesium智慧地铁教程(5)Cesium相机控制
一、环境搭建 <script src"../cesium1.99/Build/Cesium/Cesium.js"></script> <link rel"stylesheet" href"../cesium1.99/Build/Cesium/Widgets/widgets.css"> 关键配置点: 路径验证:确保相对路径.…...

DAY 47
三、通道注意力 3.1 通道注意力的定义 # 新增:通道注意力模块(SE模块) class ChannelAttention(nn.Module):"""通道注意力模块(Squeeze-and-Excitation)"""def __init__(self, in_channels, reduction_rat…...

系统设计 --- MongoDB亿级数据查询优化策略
系统设计 --- MongoDB亿级数据查询分表策略 背景Solution --- 分表 背景 使用audit log实现Audi Trail功能 Audit Trail范围: 六个月数据量: 每秒5-7条audi log,共计7千万 – 1亿条数据需要实现全文检索按照时间倒序因为license问题,不能使用ELK只能使用…...

spring:实例工厂方法获取bean
spring处理使用静态工厂方法获取bean实例,也可以通过实例工厂方法获取bean实例。 实例工厂方法步骤如下: 定义实例工厂类(Java代码),定义实例工厂(xml),定义调用实例工厂ÿ…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...
)
Typeerror: cannot read properties of undefined (reading ‘XXX‘)
最近需要在离线机器上运行软件,所以得把软件用docker打包起来,大部分功能都没问题,出了一个奇怪的事情。同样的代码,在本机上用vscode可以运行起来,但是打包之后在docker里出现了问题。使用的是dialog组件,…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Python Ovito统计金刚石结构数量
大家好,我是小马老师。 本文介绍python ovito方法统计金刚石结构的方法。 Ovito Identify diamond structure命令可以识别和统计金刚石结构,但是无法直接输出结构的变化情况。 本文使用python调用ovito包的方法,可以持续统计各步的金刚石结构,具体代码如下: from ovito…...

MySQL 8.0 事务全面讲解
以下是一个结合两次回答的 MySQL 8.0 事务全面讲解,涵盖了事务的核心概念、操作示例、失败回滚、隔离级别、事务性 DDL 和 XA 事务等内容,并修正了查看隔离级别的命令。 MySQL 8.0 事务全面讲解 一、事务的核心概念(ACID) 事务是…...
