26. 删除排序数组中的重复项、Leetcode的Python实现
博客主页:🏆看看是李XX还是李歘歘 🏆
🌺每天分享一些包括但不限于计算机基础、算法等相关的知识点🌺
💗点关注不迷路,总有一些📖知识点📖是你想要的💗
⛽️今天的内容是 Leetcode 26. 删除排序数组中的重复项 ⛽️💻💻💻
26. 删除排序数组中的重复项
给你一个 升序排列 的数组 nums ,请你 原地 删除重复出现的元素,使每个元素 只出现一次 ,返回删除后数组的新长度。元素的 相对顺序 应该保持 一致 。
由于在某些语言中不能改变数组的长度,所以必须将结果放在数组nums的第一部分。更规范地说,如果在删除重复项之后有 k 个元素,那么 nums 的前 k 个元素应该保存最终结果。
将最终结果插入 nums 的前 k 个位置后返回 k 。
不要使用额外的空间,你必须在 原地 修改输入数组 并在使用 O(1) 额外空间的条件下完成。
判题标准:
系统会用下面的代码来测试你的题解:
int[] nums = [...]; // 输入数组
int[] expectedNums = [...]; // 长度正确的期望答案
int k = removeDuplicates(nums); // 调用
assert k == expectedNums.length;
for (int i = 0; i < k; i++) {
assert nums[i] == expectedNums[i];
}
如果所有断言都通过,那么您的题解将被 通过。
示例 1:
输入:nums = [1,1,2]
输出:2, nums = [1,2,_]
解释:函数应该返回新的长度 2 ,并且原数组 nums 的前两个元素被修改为 1, 2 。不需要考虑数组中超出新长度后面的元素。
示例 2:
输入:nums = [0,0,1,1,1,2,2,3,3,4]
输出:5, nums = [0,1,2,3,4]
解释:函数应该返回新的长度 5 , 并且原数组 nums 的前五个元素被修改为 0, 1, 2, 3, 4 。不需要考虑数组中超出新长度后面的元素。
提示:
0 <= nums.length <= 3 * 104
-104 <= nums[i] <= 104
nums 已按 升序 排列
双指针:count表示数量以及当前应该插入不同值的位置
class Solution:def removeDuplicates(self, nums: List[int]) -> int:i,j=0,1while(j<len(nums)):if nums[i]!=nums[j] :i+=1nums[i]=nums[j]j+=1return i+1
相关文章:

26. 删除排序数组中的重复项、Leetcode的Python实现
博客主页:🏆看看是李XX还是李歘歘 🏆 🌺每天分享一些包括但不限于计算机基础、算法等相关的知识点🌺 💗点关注不迷路,总有一些📖知识点📖是你想要的💗 ⛽️今…...

荣耀推送服务消息分类标准
前言 为了提升终端用户的推送体验、营造良好可持续的通知生态,荣耀推送服务将对推送消息进行分类管理。 消息分类 定义 荣耀推送服务将根据应用类型、消息内容和消息发送场景,将推送消息分成服务通讯和资讯营销两大类别。 服务通讯类,包…...
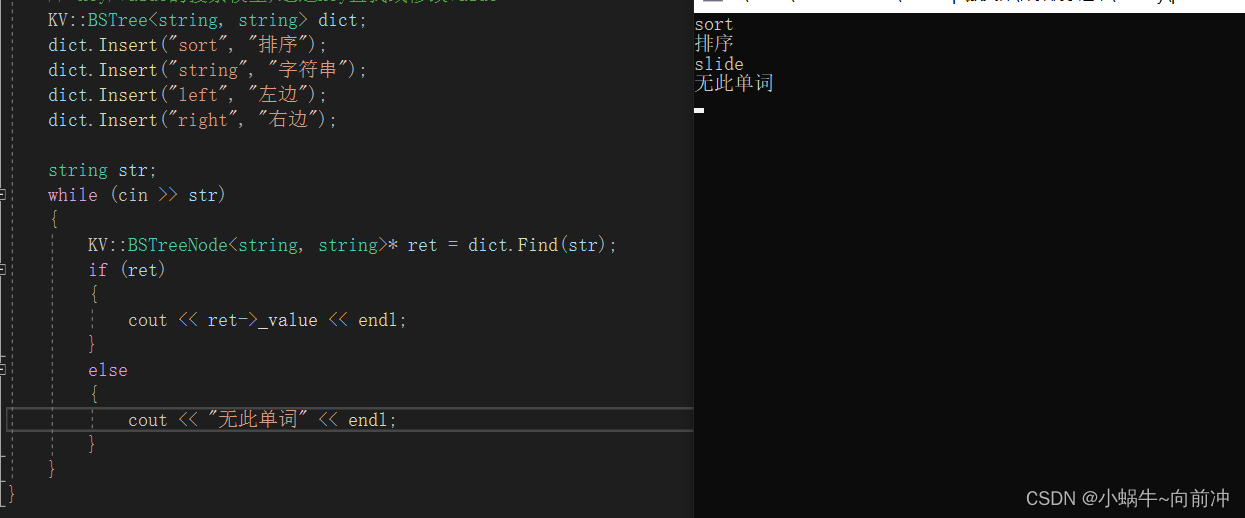
[数据结构]-二叉搜索树
前言 作者:小蜗牛向前冲 名言:我可以接受失败,但我不能接受放弃 如果觉的博主的文章还不错的话,还请点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正。 目录 一、二叉搜…...

力扣每日一题79:单词搜索
题目描述: 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格…...

ChatGPT如何应对用户提出的道德伦理困境?
ChatGPT在应对用户提出的道德伦理困境时,需要考虑众多复杂的因素。道德伦理问题涉及到价值观、原则、社会和文化背景,以及众多伦理理论。ChatGPT的设计和应用需要权衡各种考虑因素,以确保它不仅提供有用的信息,而且遵循伦理标准。…...
)
SpringBoot运行流程源码分析------阶段三(Spring Boot外化配置源码解析)
Spring Boot外化配置源码解析 外化配置简介 Spring Boot设计了非常特殊的加载指定属性文件(PropertySouce)的顺序,允许属性值合理的覆盖,属性值会以下面的优先级进行配置。home目录下的Devtool全局设置属性(~/.sprin…...
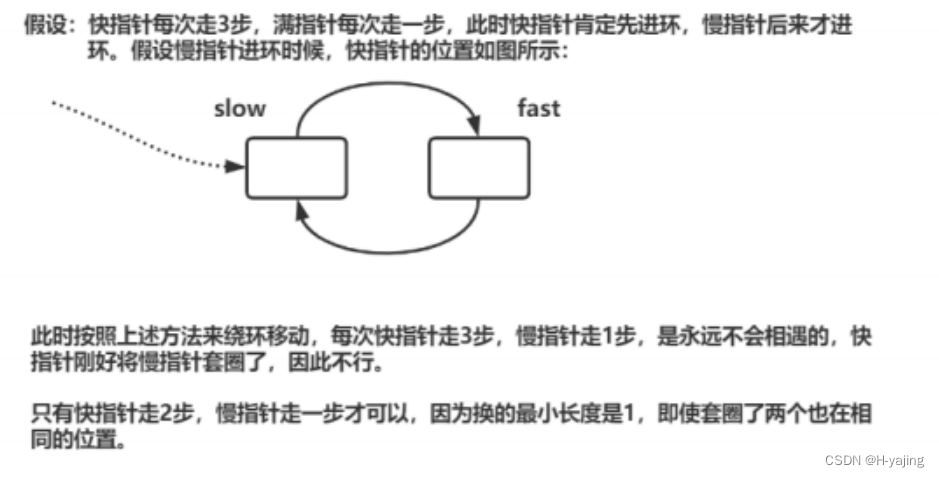
环形链表-力扣
一、题目描述 题目链接:力扣(LeetCode)官网 - 全球极客挚爱的技术成长平台 二、题解 解题思路: 快慢指针,即慢指针一次走一步,快指针一次走两步,两个指针从链表起始位置开始运行,…...

人生岁月年华
人生很长吗?不知道。只知道高中坐在教室里,闹哄哄的很难受。也记得上班时无聊敲着代码也很难受。 可是人生也不长。你没有太多时间去试错,你没有无限的时间精力去追寻你认为的高大上。 人生是何体验呢?人生的感觉很多吧。大多数…...
电脑QQ如何录制视频文件?
听说QQ可以录制视频,还很方便,请问该如何录制呢?是需要先打开QQ才可以录制吗?还是可以直接使用快捷键进行录制呢?录制的质量又如何呢? 不要着急,既然都打开这篇文章看了,那小编今天…...

python:多波段遥感影像分离成单波段影像
作者:CSDN @ _养乐多_ 在遥感图像处理中,我们经常需要将多波段遥感影像拆分成多个单波段图像,以便进行各种分析和后续处理。本篇博客将介绍一个用Python编写的程序,该程序可以读取多波段遥感影像,将其拆分为单波段图像,并保存为单独的文件。本程序使用GDAL库来处理遥感影…...

天堂2游戏出错如何解决
运行游戏时出现以下提示:“the game may not be consistant because AGP is deactivated please activate AGP for consistancy” 这个问题的原因可能是由于您的显示卡的驱动或者主板的显示芯片组的驱动不是新开。或您虽然已经更新了您的显示卡的驱动程序࿰…...
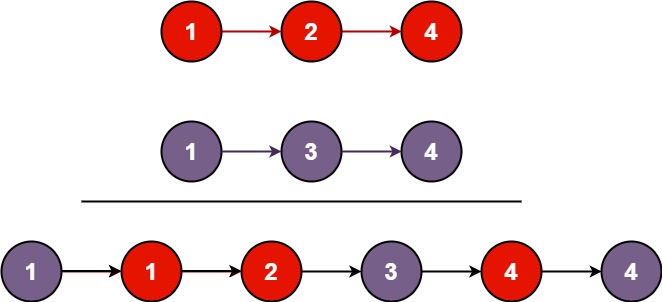
『力扣刷题本』:合并两个有序链表(递归解法)
一、题目 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 示例 1: 输入:l1 [1,2,4], l2 [1,3,4] 输出:[1,1,2,3,4,4]示例 2: 输入:l1 [], l2 [] 输出&#x…...
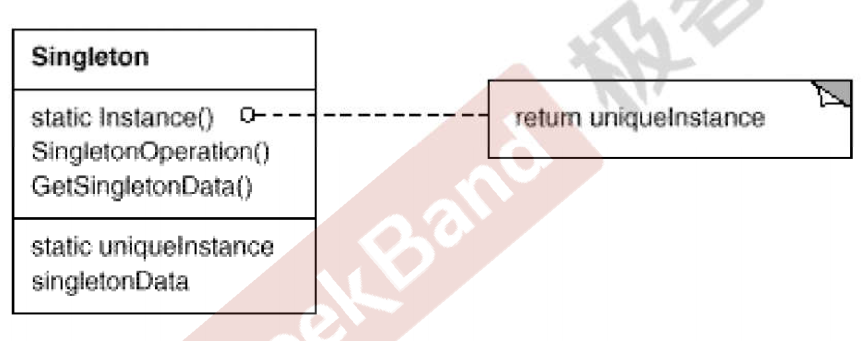
C++设计模式_12_Singleton 单件模式
在之前的博文C57个入门知识点_44:单例的实现与理解中,已经详细介绍了单例模式,并且根据其中内容,单例模式已经可以在日常编码中被使用,本文将会再做梳理。 Singleton 单件模式可以说是最简单的设计模式,但由…...
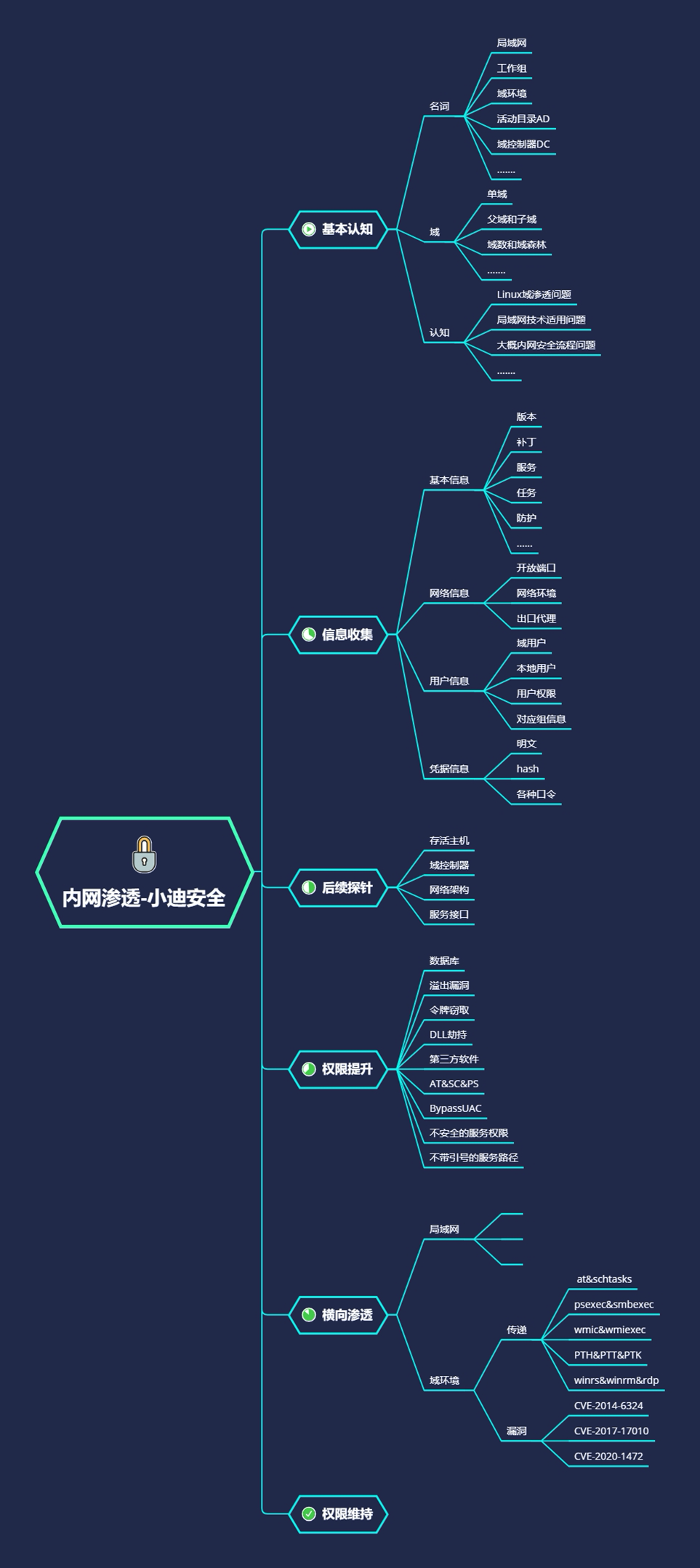
67 内网安全-域横向smbwmi明文或hash传递
#知识点1: windows2012以上版本默认关闭wdigest,攻击者无法从内存中获取明文密码windows2012以下版本如安装KB2871997补丁,同样也会导致无法获取明文密码针对以上情况,我们提供了4种方式解决此类问题 1.利用哈希hash传递(pth,ptk等…...

面向对象(类/继承/封装/多态)详解
简介: 面向对象编程(Object-Oriented Programming,OOP)是一种广泛应用于软件开发的编程范式。它基于一系列核心概念,包括类、继承、封装和多态。在这篇详细的解释中,我们将探讨这些概念,并说明它们如何在P…...

【Python机器学习】零基础掌握GradientBoostingRegressor集成学习
如何精准预测房价? 当人们提到房价预测时,很多人可能会想到房地产经纪人或专业的评估师。但是,有没有一种更科学、更精确的方法来预测房价呢?答案是有的,这就要用到机器学习中的一种算法——梯度提升回归(Gradient Boosting Regressor)。 假设现在有一组房屋数据,包括…...

【tio-websocket】12、应用层包—Packet
Packet 介绍 Packet 是用于表述业务数据结构的,我们通过继承 Packet 来实现自己的业务数据结构,对于各位而言,把 Packet 看作是一个普通的 VO 对象即可。 public class Packet implements java.io.Serializable, Cloneable {private static Logger log = LoggerFac…...
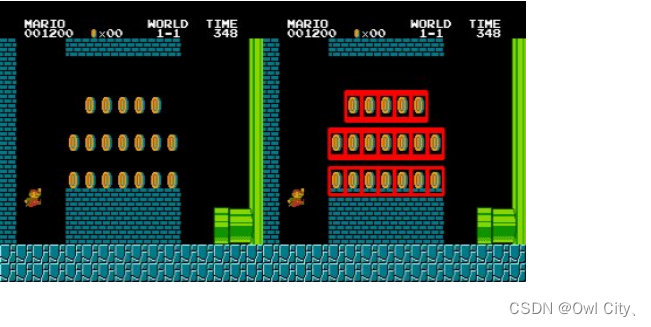
OpenCV官方教程中文版 —— 模板匹配
OpenCV官方教程中文版 —— 模板匹配 前言一、原理二、OpenCV 中的模板匹配三、多对象的模板匹配 前言 在本节我们要学习: 使用模板匹配在一幅图像中查找目标 函数:cv2.matchTemplate(),cv2.minMaxLoc() 一、原理 模板匹配是用来在一副大…...
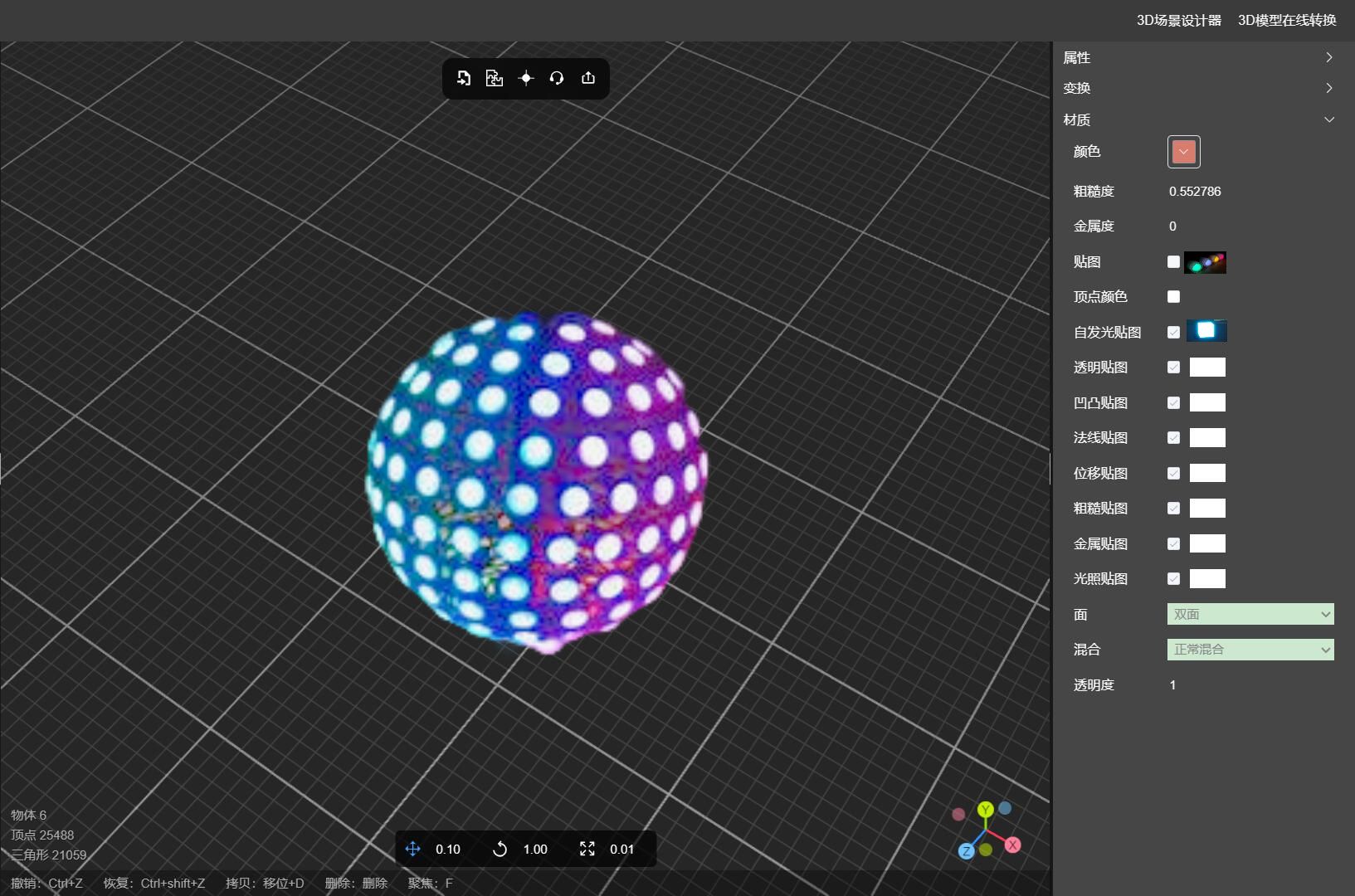
如何为3D模型设置自发光材质?
1、自发光贴图的原理 自发光贴图是一种纹理贴图,用于模拟物体自发光的效果。其原理基于光的发射和反射过程。 在真实世界中,物体自发光通常是由于其本身具有能够产生光的属性,如荧光物质、发光材料或光源本身。为了在计算机图形中模拟这种效…...
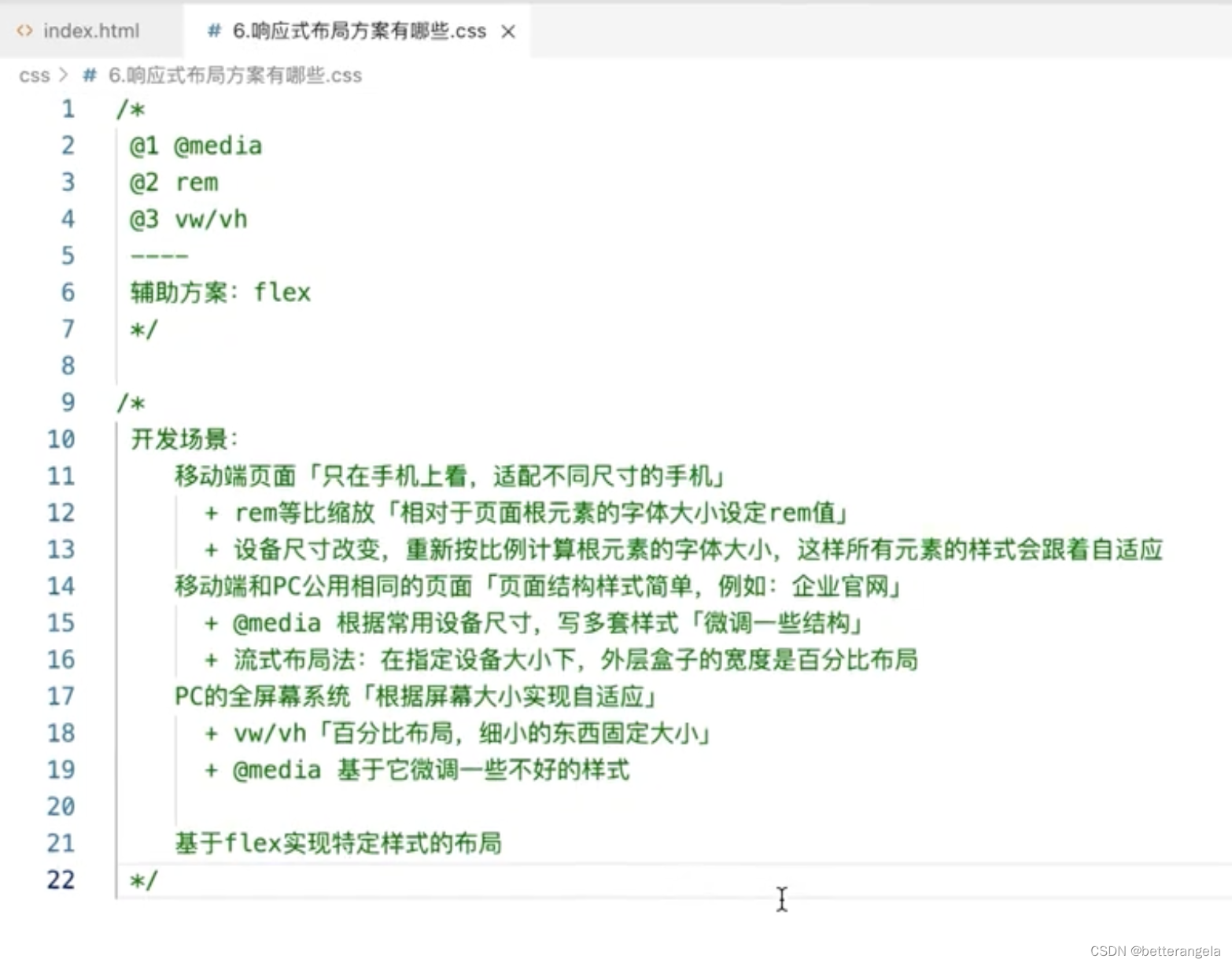
UI组件库基础
UI组件库 全局组件* 全局注册组件 & 并且使用了require.context 模块化编程 & webpack打包 const install(Vue)>{const contextrequire.context(.,true,/\.vue$/)context.keys().forEach(fileName>{const modulecontext(fileName)Vue.component(module.default.n…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

测试markdown--肇兴
day1: 1、去程:7:04 --11:32高铁 高铁右转上售票大厅2楼,穿过候车厅下一楼,上大巴车 ¥10/人 **2、到达:**12点多到达寨子,买门票,美团/抖音:¥78人 3、中饭&a…...

力扣-35.搜索插入位置
题目描述 给定一个排序数组和一个目标值,在数组中找到目标值,并返回其索引。如果目标值不存在于数组中,返回它将会被按顺序插入的位置。 请必须使用时间复杂度为 O(log n) 的算法。 class Solution {public int searchInsert(int[] nums, …...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

springboot 日志类切面,接口成功记录日志,失败不记录
springboot 日志类切面,接口成功记录日志,失败不记录 自定义一个注解方法 import java.lang.annotation.ElementType; import java.lang.annotation.Retention; import java.lang.annotation.RetentionPolicy; import java.lang.annotation.Target;/***…...

[论文阅读]TrustRAG: Enhancing Robustness and Trustworthiness in RAG
TrustRAG: Enhancing Robustness and Trustworthiness in RAG [2501.00879] TrustRAG: Enhancing Robustness and Trustworthiness in Retrieval-Augmented Generation 代码:HuichiZhou/TrustRAG: Code for "TrustRAG: Enhancing Robustness and Trustworthin…...
