【C++】mapset的底层结构 -- AVL树(高度平衡二叉搜索树)
前面我们对 map / multimap / set / multiset 进行了简单的介绍,可以发现,这几个容器有个共同点是:其底层都是按照二叉搜索树来实现的。但是二叉搜索树有其自身的缺陷,假如往树中插入的元素有序或者接近有序,二叉搜索树就会退化成单支树,时间复杂度会退化成 O(N),因此 map、set 等关联式容器的底层结构是对二叉树进行了平衡处理,即采用 平衡树 来实现。
一、AVL树(高度平衡二叉搜索树)
1、概念
二叉搜索树虽可以缩短查找的效率,但如果数据有序或接近有序二叉搜索树将退化为单支树,查找元素相当于在顺序表中搜索元素,效率低下。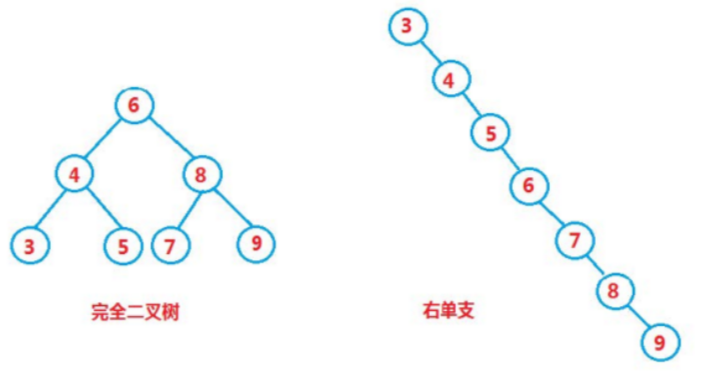
- 最优情况下,有 n 个结点的二叉搜索树为完全二叉树,查找效率为:O(log₂N)。
- 最差情况下,有 n 个结点的二叉搜索树退化为单支树,查找效率为:O(N)。
因此,两位俄罗斯的数学家 G.M.Adelson-Velskii 和 E.M.Landis 在 1962 年发明了一种解决上述问题的方法:当向二叉搜索树中 插入新结点 后,如果能 保证每个结点的左右子树高度之差的绝对值不超过 1 (需要对树中的结点进行调整),即可降低树的高度,从而减少平均 搜索长度。
- 它的左右子树都是 AVL 树。
- 左右子树高度之差(简称平衡因子)的绝对值不超过 1(-1/0/1)。
如果一棵二叉搜索树是高度平衡的,它就是 AVL 树。如果它有 n 个结点,其高度可保持在 O(log₂n),搜索时间复杂度 O(log₂n)。
为什么左右子树高度差不规定成0呢?
因为在 2、4 等节点数的情况下,不可能做到左右高度相等的情况。
2、AVL 树节点的定义
AVL 树节点是一个 三叉链结构,除了 指向左右孩子的指针,还有一个 指向其父亲的指针,数据域是键值对,即 pair 对象,还引入了平衡因子,用来判断是否需要进行平衡操作。
// AVL树节点的定义(KV模型)
template<class K, class V>
struct AVLTreeNode
{AVLTreeNode<T>* _left; // 该节点的左孩子AVLTreeNode<T>* _right; // 该节点的右孩子AVLTreeNode<T>* _parent; // 该节点的双亲指针pair<K, V> _kv; // 键值对int _bf; // 该节点的平衡因子(balance factor) = 右子树高度-左子树高度// 构造函数AVLTreeNode(const pari<K, V>& kv): _left(nullptr), _right(nullptr), _parent(nullptr), _kv(kv), _bf(0){}
};// AVL树的定义(KV模型)
template<class K, class V>
class AVLTree
{typedef AVLTreeNode<K, V> Node;
public:// 成员函数private:Node* _root;
}3、AVL树的插入
AVL 树就是在二叉搜索树的基础上引入了平衡因子,因此 AVL 树也可以看成是二叉搜索树。那么 AVL 树的插入过程可以分为两步:
- 按照二叉搜索树的方式插入新节点到 AVL 树中。
- 新节点插入后,AVL 树的平衡性可能会遭到破坏,此时就需要更新平衡因子,并检测是否破坏了 AVL 树的平衡(控制树的平衡(旋转操作))。
// 插入节点
bool Insert(const pair<K, V>& kv)
{// 如果树为空,则直接插入节点if (_root == nullptr){_root = new Node(kv);return true;}// 如果树不为空,找到适合插入节点的空位置Node* parent = nullptr; // 记录当前节点的父亲Node* cur = _root; // 记录当前节点while (cur) // while循环结束,说明找到适合插入节点的空位置了{if(kv.first > cur->_kv.first) // 插入节点键值k大于当前节点{parent = cur;cur = cur->_right;}else if(kv.first < cur->_kv.first) // 插入节点键值k小于当前节点{ parent = cur;cur = cur->_left;}else // 插入节点键值k等于当前节点{return false;}}// 插入新节点cur = new Node(kv); // 申请新节点// 判断当前节点是父亲的左孩子还是右孩子if (cur->_kv.first > parent->_kv.first){parent->_right = cur; }else{parent->_left = cur;}cur->_parent = parent;// 控制平衡// 1、更新平衡因子// ...return true;
}⚪更新平衡因子
(1)插入新节点cur 插入后,parent 的平衡因子一定需要调整,在插入之前,parent 的平衡因子分为三种情况:-1,0,1,分以下两种情况:
- 如果 cur 插入到 新节点父亲(parent) 的左侧,只需给 父亲(parent) 的平衡因子--(
_bf--)即可。- 如果 cur 插入到 新节点父亲(parent) 的右侧,只需给 父亲(parent) 的平衡因子++(
_bf++)即可。
(2)新节点父亲的平衡因子更新以后,又会分为 3 种情况:
此时:parent的平衡因子可能有三种情况:0,正负 1, 正负 2。
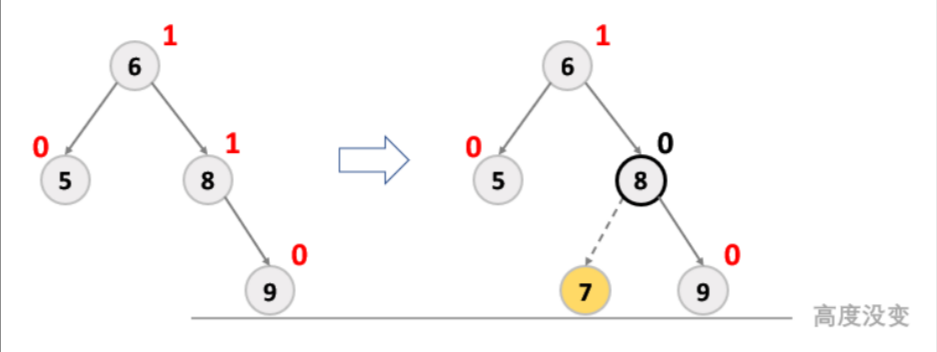
- 如果更新以后,parent 的平衡因子是 0(则说明插入之前 parent 的平衡因子之前一定为 1/-1),说明父亲所在子树高度没变(因为把矮的那边给填补上了),此时满足 AVL 树的性质,插入成功,不需要继续往上更新。
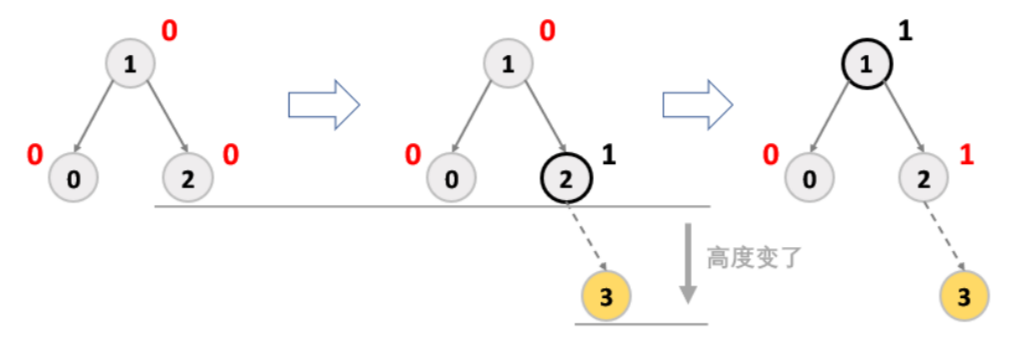
- 如果更新以后,parent 的平衡因子是 1/-1(则说明插入之前 parent 的平衡因子 一定为 0),说明父亲所在子树高度增加,需要继续往上更新。(最坏情况:往上一直更新到根节点)。
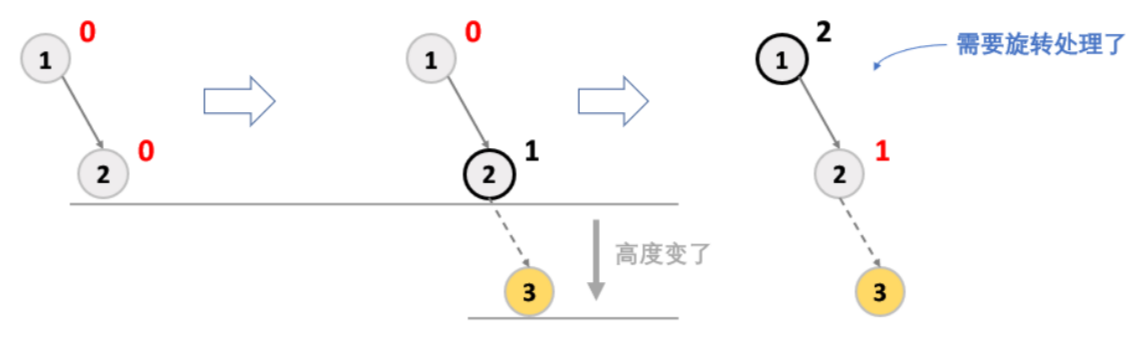
- 如果更新以后,parent 的平衡因子是 2/-2,说明父亲所在子树出现了不平衡,需要对其进行旋转处理。
// 插入节点
bool Insert(const pair<K, V>& kv)
{// 控制平衡// 1、更新平衡因子while (parent) // 最坏情况:更新到根节点{// 更新双亲的平衡因子if (cur == parent->_left) // 新节点插入在父亲的左边parent->_bf--;else // 新节点插入在父亲的右边parent->_bf++;// 更新后检测双亲的平衡因子if (0 == pParent->_bf){ break;}//else if (1 == parent->_bf || -1 == parent->_bf)else if (abs(parent->_bf) == 1) // 插入前双亲的平衡因子是0,插入后双亲的平衡因为为1 或者 -1 ,说明以双亲为根的二叉树的高度增加了一层,因此需要继续向上调整{cur = parent;parent = cur->_parent;}else if (abs(parent->_bf) == 2) // 双亲的平衡因子为正负2,违反了AVL树的平衡性,需要对以parent为根的树进行旋转处理{// 1、父节点的右边高,左边低,需要往左旋if (parent->_bf == 2 && cur->_bf == 1) {RotateL(parent); // 左单旋}// 2、父节点的左边高,右边低,需要往右旋else if ((parent->_bf == -2 && cur->_bf == -1)){RotateR(parent); // 右单旋}// 3、父节点的左边高,且父节点左孩子的右边高else if (parent->_bf == -2 && cur->_bf == 1) {RotateLR(parent); // 左右双旋}// 4、父节点的右边高,且父节点右孩子的左边高else if (parent->_bf == 2 && cur->_bf == -1){RotateRL(parent); // 右左双旋}break; // 旋转完成,树已平衡,退出循环}// 除了上述3种情况,平衡因子不可能有其它的值,报错处理else{assert(false);}}return true;
}4、AVL树的旋转
如果在一棵原本是平衡的 AVL 树中插入一个新节点,可能造成不平衡,此时必须调整树的结构,使之平衡化。根据节点插入位置的不同,AVL 树的旋转分为四种:
旋转的本质:在遵循二叉搜索树的规则下,让左右均衡,降低整棵树的高度。
该进行哪种旋转操作?
引发旋转的路径是直线就是单旋,如果是折线就是双旋。
注意:此处看到的树,可能是一颗完整的树,也可能是一颗子树。
(1)新节点插入较高左子树的左侧 —— 左左:右单旋
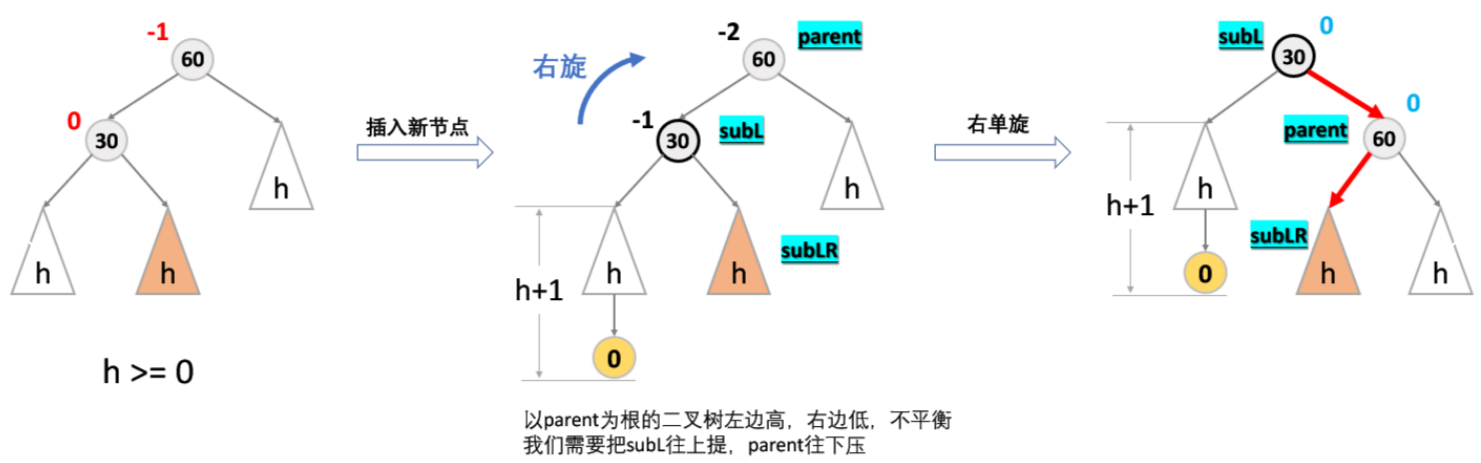
将新的节点插入到了 parent 左孩子的左子树上,导致的不平衡的情况。
上图在插入前,AVL 树是平衡的,新节点插入到 30 的左子树(注意:此处不是左孩子)中,30 左子树增加了一层,导致以 60 为根的二叉树不平衡,要让 60 平衡,只能将 60 左子树的高度减少一层,右子树增加一层,即将左子树往上提,这样 60 转下来,因为 60 比 30 大,只能将其放在 30 的右子树,而如果 30 有右子树,右子树根的值一定大于 30,小于 60,只能将其放在 60 的左子树,旋转完成后,更新节点的平衡因子即可。
【引发右单旋的条件】
- 父亲左边高,右边低,所以要让父亲往右旋。
- parent 的平衡因子为 -2,parent 左孩子平衡因子为 -1,观察发现,平衡因子都是负数,说明是左边高,也说明了引发旋转的路径是一条直线,所以我们要右旋操作。
【右单旋操作】
1、让 subL 的右子树 subLR 成为 parent 的左子树(因为 subLR 的右子树根节点值 > 30,< 60)。
2、让 parent 成为 subL 的右子树(因为 60 > 30)。
3、让 subL 变成这个子树的根。这一步操作前需要先判断下:parent 是根节点,还是一个普通子树
- 如果是根节点,旋转完成后,则更新 subL 为新的根节点。
- 如果是普通子树(可能是某个节点的左子树,也可能是右子树,这里作一个判断),然后更新 subL 为这个子树的根节点。
4、根据树的结构,更新 parent 和 subL 的平衡因子为 0。
在旋转过程中,更新双亲指针的指向,有以下几种情况需要考虑:
- 30 节点的右孩子可能存在,也可能不存在。(subL 的右子树 subLR 可能存在,也可能为空。当不为空时才更新 subL 右子树 subLR 的双亲指针指向)。
- 60 可能是根节点,也可能是子树。(旋转完成后,subL 的双亲节点,可能是空,也可能是 parent 原先的父节点。所以在更新 subL 的双亲指针前需要判断下)。
依次调整 subLR、parent、subL 的位置和双亲指针的指向。
// 右单旋
void _RotateR(Node* parent)
{ Node* subL = parent->_left; // subL : parent的左孩子Node* subLR = subL->_right; // subLR : parent左孩子的右孩子// 旋转完成之后,让subL的右子树subLR成为parent的左子树parent->_left = subLR;// 如果subLR存在,更新subLR的双亲指针,指向parentif (subLR){subLR->_parent = parent;}// 因为parent可能是棵子树,因此在更新其双亲前必须先保存parent的父节点Node* ppNode = parent->_parent;// 让parent成为subL的右子树subL->_right = parent;// 更新parent的双亲指针,指向subLparent->_parent = subL;// 如果parent是根节点,根新指向根节点的指针if (_root == parent){_root = subL; // 更新subL为新的根subL->_parent = nullptr; // 更新subL的双亲指针,指向空}// parent不是根节点,就是一个普通子树else{// 判断parent原先是左孩子还是右孩子if (ppNode->_left == parent){ppNode->_left = subL; // parent原先的双亲节点接管subL,subL为这个子树的根}else{ppNode->_right = subL;}subL->_parent = ppNode; // 更新subL的双亲指针}// 根据调整后的结构更新部分节点的平衡因子parent->_bf = pSubL->_bf = 0;
}(2)新节点插入较高右子树的右侧 —— 右右:左单旋
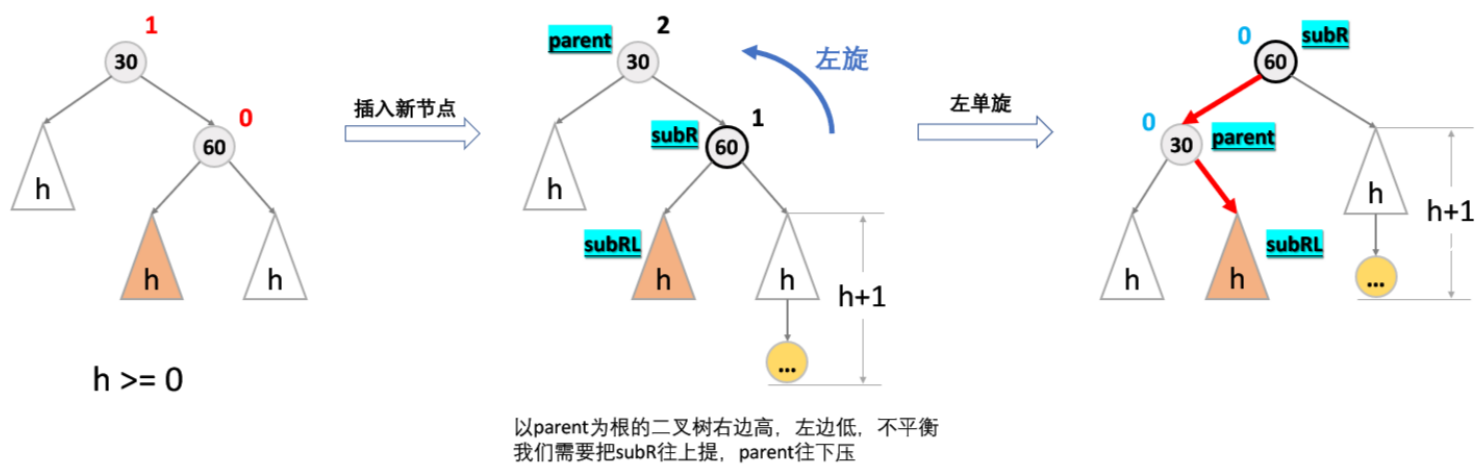
【引发左单旋的条件】
- 父亲右边高,左边低,所以要让父亲往左旋。
- parent 的平衡因子为 2,parent 左孩子平衡因子为 1,观察发现,平衡因子都是正数,说明是右边高,也说明了引发旋转的路径是一条直线,所以我们要右旋操作。
【右单旋操作】
1、让 subR 的左子树 subRL 成为 parent 的右子树(因为 subRL 的左子树根节点值 > 30,< 60)。
2、让 parent 成为 subR 的左子树(因为 30 < 60)。
3、让 subR 变成这个子树的根。这一步操作前需要先判断下:parent 是根节点,还是一个普通子树
- 如果是根节点,旋转完成后,则更新 subR 为新的根节点。
- 如果是普通子树(可能是某个节点的左子树,也可能是右子树,这里作一个判断),然后更新 subR 为这个子树的根节点。
4、根据树的结构,更新 parent 和 subR 的平衡因子为 0。
在旋转过程中,更新双亲指针的指向,有以下几种情况需要考虑:
- subR 的左子树 subRL 可能存在,也可能为空。(当不为空时才更新 subR 左子树 subRL 的双亲指针指向)。
- 旋转完成后,subR 的双亲节点,可能是空,也可能是 parent 原先的父节点。(所以更新 subR 的双亲指针前需要判断下)。
依次调整 subRL、parent、subR 的位置和双亲指针的指向。
// 左单旋
void treeRotateLeft(Node* parent)
{Node* subR = parent->_right; // subR:父亲的右孩子Node* subRL = subR->_left; // subRL:父亲的右孩子的左孩子(大于父亲,小于subR)// 让subRL成为父亲的右子树parent->_right = subRL;// 如果subRL不为空if (subRL){subRL->_parent = parent; // 更新subRL双亲指针,指向parent}// 因为parent可能是棵子树,因此在更新其双亲前必须先保存parent的父节点Node* ppNode = parent->_parent;// 让parent成为subR的左子树subR->_left = parent; // 更新parent双亲指针的指向parent->_parent = subR;// 判断parent是不是根节点if (parent == _root){_root = subR; // subR为新的根subR->_parent = nullptr; // subR双亲指针指向空}// 不是根节点,就是一个普通子树else{// 判断parent原先是左孩子还是右孩子if (ppNode->_left == parent){ppNode->_left = subR; // parent原先的双亲节点接管subR,subR为这个子树的根}else{ppNode->_right = subR;}subR->_parent = ppNode; // 更新subR的双亲指针}// 根据树的结构,更新parent和subR的平衡因子parent->_bf = subR->_bf = 0;
}
(3)新节点插入较高左子树的右侧 —— 左右:先左单旋再右单旋(左右双旋)
将新的节点插入到了 parent 左孩子的右子树上,导致的不平衡的情况。
这时我们需要的是先对 parent 的右孩子进行一次左旋,再对 parent 进行一次右旋。
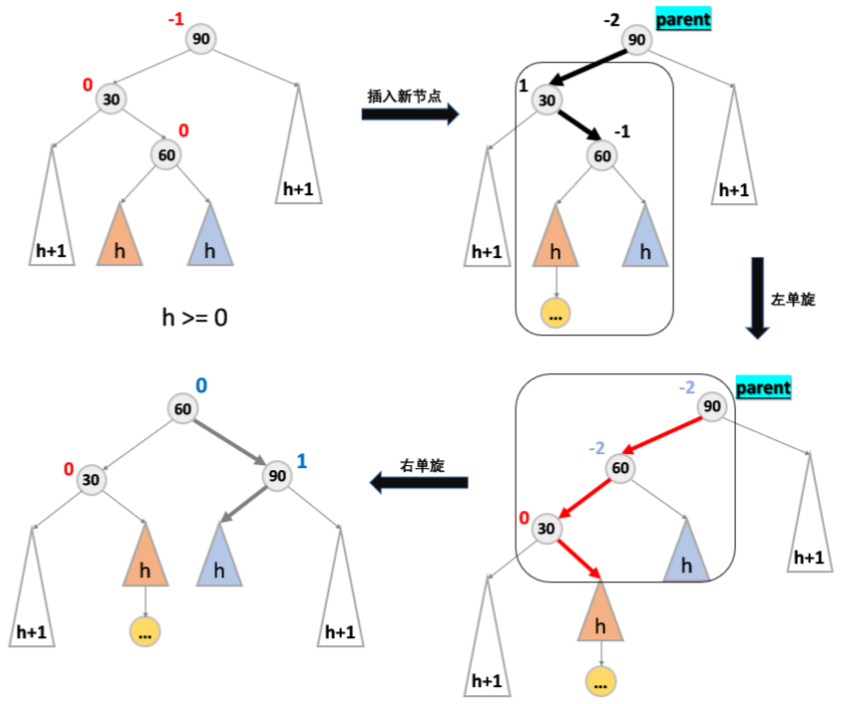
将双旋变成单旋后再旋转,即:先对 30 进行左单旋,然后再对 90 进行右单旋,旋转完成后再考虑平衡因子的更新。
旋转之前,60 的平衡因子可能是 -1/0/1,旋转完成之后,根据情况对其他节点的平衡因子进行调整。
【h == 0】

【引发双旋的条件】
引发旋转的路径是直线就是单旋,如果是折线就是双旋。
parent 的平衡因子为 -2,parent 左孩子的平衡因子为 1,观察发现,平衡因子是一负一正,说明左孩子右边高,父亲左边高,也说明了引发旋转的路径是一条折线,所以我们要先对左孩子进行左旋操作,再对父亲进行右旋操作。
左右双旋操作后,根据树的结构,更新平衡因子时,需要注意:
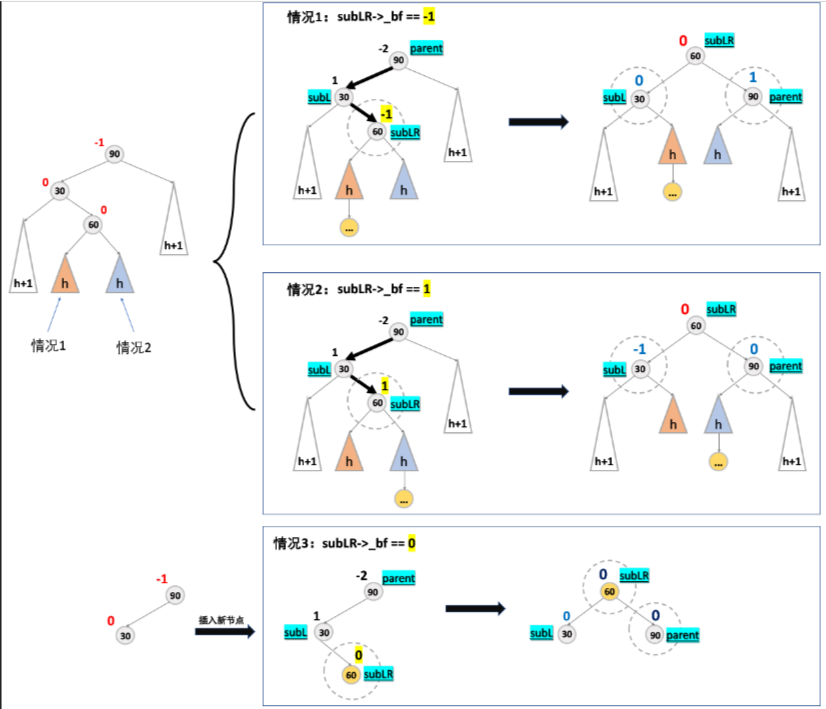
插入新节点的位置不同,经过左右双旋后,得到树的结构也会有所不同,平衡因子也会有所不同,有以下三种情况:
- 新节点插入到了 parent 左孩子的右子树的左边。
- 新节点插入到了 parent 左孩子的右子树的右边。
- 新节点就是 parent 左孩子的右孩子。
这里可以观察到一个现象,根据这个现象就很好推出旋转后的平衡因子:
节点 60 的左右子树被分走了,左子树最终成为了节点 30 的右子树,右子树最终成了节点 90 的左子树。
void _RotateLR(PNode pParent)
{Node* subL = parent->_left; // 记录parent的左孩子Node* subLR = subL->_right; // 记录parent的左孩子的右孩子// 旋转之前,因为插入新节点的位置不同,subLR的平衡因子可能是-1/0/1int bf = subLR->_bf; // 记录subLR的平衡因子// 先对parent的左孩子进行左单旋RotateL(parent->_left);// 再对parent进行右单旋RotateR(parent);// 旋转完成之后,根据情况对其他节点的平衡因子进行调整subLR->_bf = 0;if (bf == -1){parent->_bf = 1;subL->_bf = 0;}else if (bf == 1){parent->_bf = 0;subL->_bf = -1;} else if (bf == 0){parent->_bf = 0;subL->_bf = 0;}else{assert(false);}
}(4)新节点插入较高右子树的左侧 —— 右左:先右单旋再左单旋(右左双旋)
将新的节点插入到了 parent 右孩子的左子树上,导致的不平衡的情况。
这时我们需要的是先对 parent 的右孩子进行一次右旋,再对 parent 进行一次左旋。
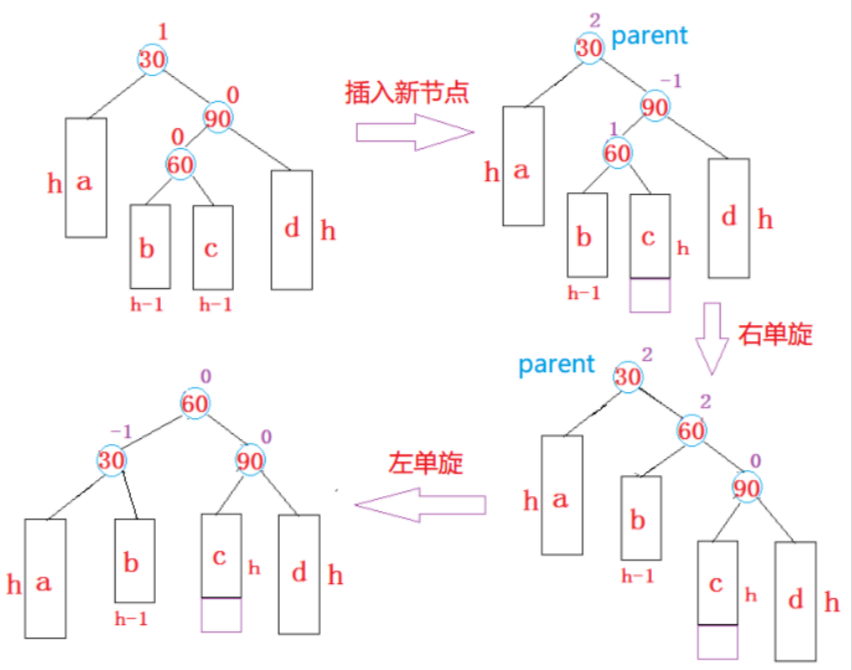
【h == 1】
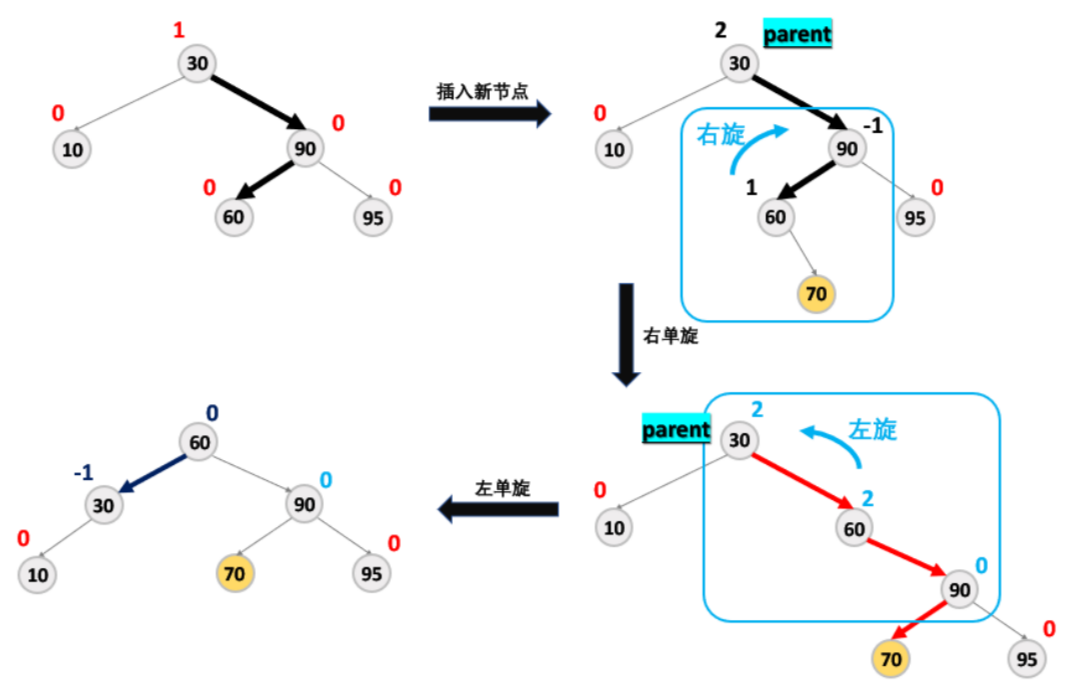
【引发双旋的条件】
引发旋转的路径是直线就是单旋,如果是折线就是双旋。
parent 的平衡因子为 2, parent 右孩子平衡因子为 -1,观察发现,平衡因子是一正一负,说明右孩子左边高,父亲右边高,也说明了引发旋转的路径是一条折线,所以我们要先对右孩子进行右旋操作,再对父亲进行左旋操作。
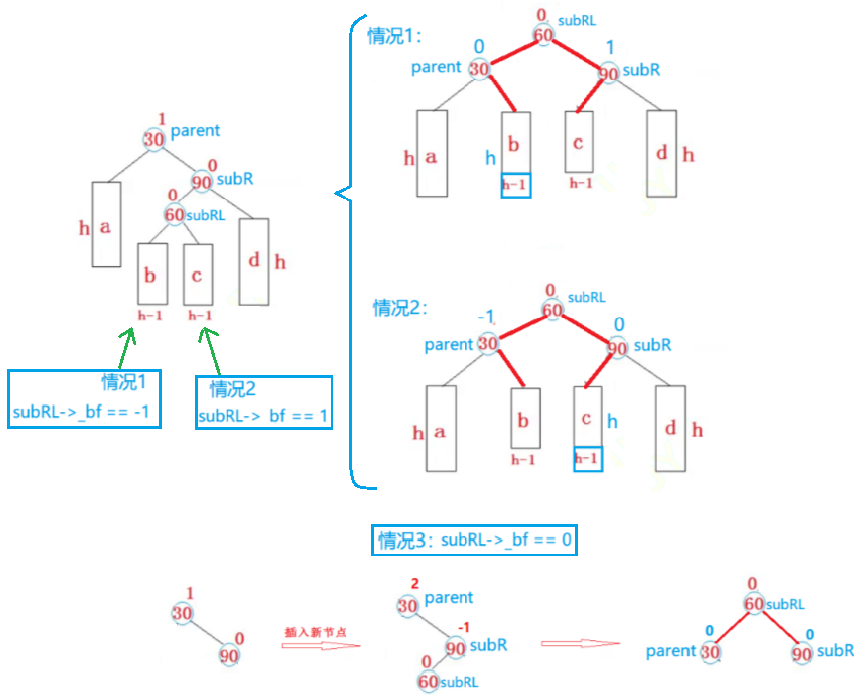
左右双旋操作后,根据树的结构,更新平衡因子时,需要注意:
插入新节点的位置不同,经过右左双旋后,得到树的结构也会有所不同,平衡因子也会有所不同,有以下三种情况:
- 新节点插入到了 parent 右孩子的左子树的左边。
- 新节点插入到了 parent 右孩子的左子树的右边。
- 新节点就是 parent 右孩子的左孩子。
这里可以观察到一个现象,根据这个现象就很好推出旋转后的平衡因子:
节点 60 的左右子树被分走了,左子树 b 最终成了节点 30 的右子树,右子树 c 最终成了节点 90 的左子树。
// 右左双旋
void treeRotateRL(Node* parent)
{Node* subR = parent->_right; // 记录parent的右孩子Node* subRL = subR->_left; // 记录parent的右孩子的左孩子// 旋转之前,因为插入新节点的位置不同,subRL的平衡因子可能为-1/0/1int bf = subRL->_bf; // 记录subRL的平衡因子RotateR(parent->_right); // 先对parent的右孩子进行右单旋RotateL(parent); // 再对parent进行左单选// 旋转完成之后,根据树的结构对其他节点的平衡因子进行调整subRL->_bf = 0;if (bf == -1){parent->_bf = 0;subR->_bf = 1;}else if (bf == 1){parent->_bf = -1;subR->_bf = 0;}else if(bf == 0){parent->_bf = 0;subR->_bf = 0;}else{assert(false);}
}【总结】假如以 parent 为根的子树不平衡,即 parent 的平衡因子为 2/-2,分以下情况考虑:1、parent 的平衡因子为 2,说明 parent 的右子树高,设 parent 的右子树的根为 subR。
- 当 subR 的平衡因子为 1 时,执行左单旋。
- 当 subR 的平衡因子为 -1 时,执行右左双旋。
2、parent 的平衡因子为 -2,说明 parent 的左子树高,设 parent 的左子树的根为 subL。
- 当 subL 的平衡因子为 -1 时,执行右单旋。
- 当 subL 的平衡因子为 1 时,执行左右双旋。
旋转完成后,原 parent 为根的子树个高度降低,已经平衡,不需要再向上更新。
5、AVL树的验证
1、验证其为二叉搜索树
- 如果中序遍历可得到一个有序的序列,就说明为二叉搜索树。
2、验证其为平衡树
- 每个节点子树高度差的绝对值不超过 1(注意节点中如果没有平衡因子)。
- 节点的平衡因子是否计算正确。
(1)首先写一个计算当前树高度的函数
// 计算当前树的高度
int Height(Node* root)
{// 当前树为空,则高度为0if (root == nullptr)return 0;// 当前树的高度 = 左右子树中高度最大的那个加1return max(Height(root->_left), Height(root->_right)) + 1;
}(2)检查AVL树是否平衡:【思路一】自顶向下的暴力解法
bool IsBalance1()
{return _IsBalance(_root);
}bool _IsBalance1(Node* root)
{// 当前树为空,说明是平衡的if (root == nullptr)return true;// 当前树不为空,计算左右子树的高度int leftHT = Height(root->_left);int rightHT = Height(root->_right);int diff = rightHT - leftHT;if (diff != root->_bf) // 检查当前树的平衡因子是否计算正确{cout << root->_kv.first << "平衡因子异常" << endl;return false;}// 左右子树高度相减的绝对值小于2,说明当前树是平衡的,则继续往下判断其它子树return abs(diff) < 2&& _IsBalance(root->_left)&& _IsBalance(root->_right);
}(3)检查AVL树是否平衡【思路二】自底向上的高效解法(动态规划,前一个子问题的解,能够用于后一个问题求解)
bool IsBalance2()
{return _IsBalance2(_root) != -1;
}int _IsBalance2(Node* root)
{// 先判断当前树的左、右子树是否平衡,再判断当前树是否平衡// 不平衡返回-1,平衡则返回当前树的高度// 当前树为空,返回高度0if (root == nullptr)return 0;// 当前树不为空,分别计算左右子树的高度int leftHeight = _IsBalance2(root->_left);int rightHeight = _IsBalance2(root->_right);int diff = rightHT - leftHT;if (diff != root->_bf) // 检查当前树的平衡因子是否计算正确{cout << "平衡因子异常:" << root->_kv.first << endl;}// 左子树高度等于-1、右子树高度等于-1、左右子树高度差的绝对值大于1,说明当前树不平衡if (leftHeight == -1 || rightHeight == -1 || abs(diff) > 1)return -1;// 运行到这里来了,说明当前树是平衡的,返回当前树的高度return max(leftHeight, rightHeight) + 1;
}(4)【思路三】
bool _IsBalanceTree3(Node* root)
{// 空树也是AVL树if (nullptr == root)return true;// 计算pRoot节点的平衡因子:即pRoot左右子树的高度差int leftHeight = _Height(root->_left);int rightHeight = _Height(root->_right);int diff = rightHeight - leftHeight;// 如果计算出的平衡因子与pRoot的平衡因子不相等,或者pRoot平衡因子的绝对值超过1,则一定不是AVL树if (diff != root->_bf || (diff > 1 || diff < -1))return false;// pRoot的左和右如果都是AVL树,则该树一定是AVL树return _IsBalanceTree3(root->_left) && _IsBalanceTree3(root->_right);}3、验证用例
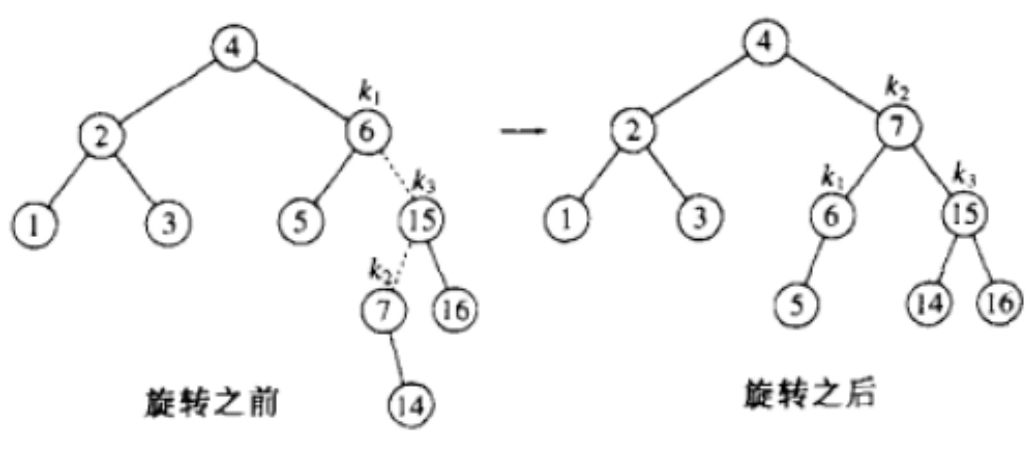
- 常规场景 1:{16, 3, 7, 11, 9, 26, 18, 14, 15}
- 特殊场景 2:{4, 2, 6, 1, 3, 5, 15, 7, 16, 14}
6、AVL树的删除(了解)
因为 AVL 树也是二叉搜索树,可按照二叉搜索树的方式将节点删除,然后再更新平衡因子,只不过与删除不同的是,删除节点后的平衡因子更新,最差情况下一直要调整到根节点的位置。具体实现可参考《算法导论》或《数据结构-用面向对象方法与C++描述》殷人昆版。
7、AVL 树的性能
AVL 树是一棵绝对平衡的二叉搜索树,其要求每个节点的左右子树高度差的绝对值都不超过 1,这样可以保证查询时高效的时间复杂度,即 O(logN)。但是如果要对 AVL 树做一些结构修改的操作,性能非常低下,比如:插入时要维护其绝对平衡,旋转的次数比较多,更差的是在删除时,有可能一直要让旋转持续到根的位置。因此,如果需要一种查询高效且有序的数据结构,而且数据的个数为静态的(即不会改变),可以考虑 AVL 树,但一个结构经常修改,就不太适合。
相关文章:

【C++】mapset的底层结构 -- AVL树(高度平衡二叉搜索树)
前面我们对 map / multimap / set / multiset 进行了简单的介绍,可以发现,这几个容器有个共同点是:其底层都是按照二叉搜索树来实现的。 但是二叉搜索树有其自身的缺陷,假如往树中插入的元素有序或者接近有序,二叉搜索…...
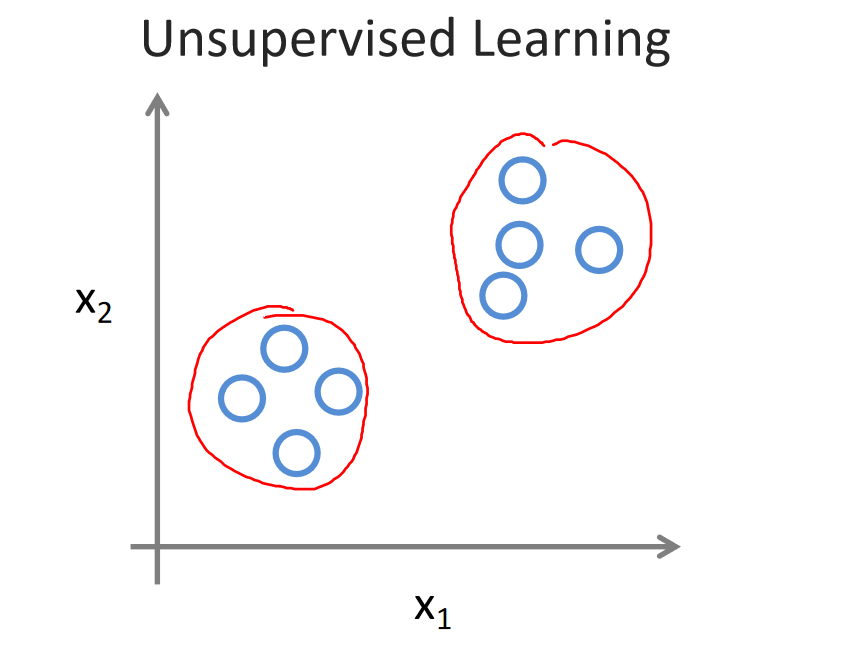
吴恩达《机器学习》1-4:无监督学习
一、无监督学习 无监督学习就像你拿到一堆未分类的东西,没有标签告诉你它们是什么,然后你的任务是自己找出它们之间的关系或者分成不同的组,而不依赖于任何人给你关于这些东西的指导。 以聚类为例,无监督学习算法可以将数据点分成…...
)
一个简单的注册页面,如有错误请指正(2.css)
这段CSS代码定义了页面的样式,让我逐个解释其功能: 1. * {}:通配符选择器,用于将页面中的所有元素设置统一的样式。这里将margins和paddings设置为0,以去除默认的边距。 2. div img {}:选择页面中所有div…...

【Unity精华一记】特殊文件夹
👨💻个人主页:元宇宙-秩沅 👨💻 hallo 欢迎 点赞👍 收藏⭐ 留言📝 加关注✅! 👨💻 本文由 秩沅 原创 👨💻 收录于专栏:uni…...
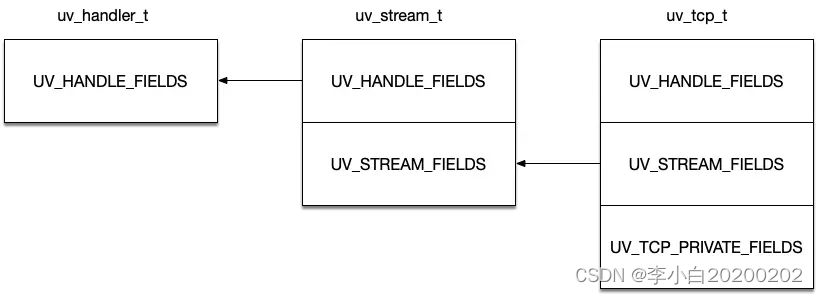
Node.js中的单线程服务器
为了解决多线程服务器在高并发的I/O密集型应用中的不足,同时避免早期简单单线程服务器的性能障碍,Node.js采用了基于"事件循环"的非阻塞式单线程模型,实现了如下两个目标: (1)保证每个请求都可以…...

如何删除数组中的某个元素?
如何删除数组中的某个元素? 例:给你一个数组 nums 和一个值 val,你需要移除所有数值等于 val 的元素,并返回移除后数组的新长度。 三种方法 1.元素前移(时间复杂度:O(N^2),空间复杂度&#x…...
Apache ActiveMQ RCE漏洞复现(CNVD-2023-69477)
0x01 产品简介 ActiveMQ是一个开源的消息代理和集成模式服务器,它支持Java消息服务(JMS) API。它是Apache Software Foundation下的一个项目,用于实现消息中间件,帮助不同的应用程序或系统之间进行通信。 0x02 漏洞概述 Apache ActiveMQ 中存…...

【BUG】Nginx转发失败解决方案
最近在做项目的时候出现了一个问题,琢磨了好久,来浅浅记录一下。 这个项目后端使用的是gateway网关和nacos实现动态的路由,前端使用nginx来管理前端资源,大体流程:浏览器发起请求,经过nginx代理,…...
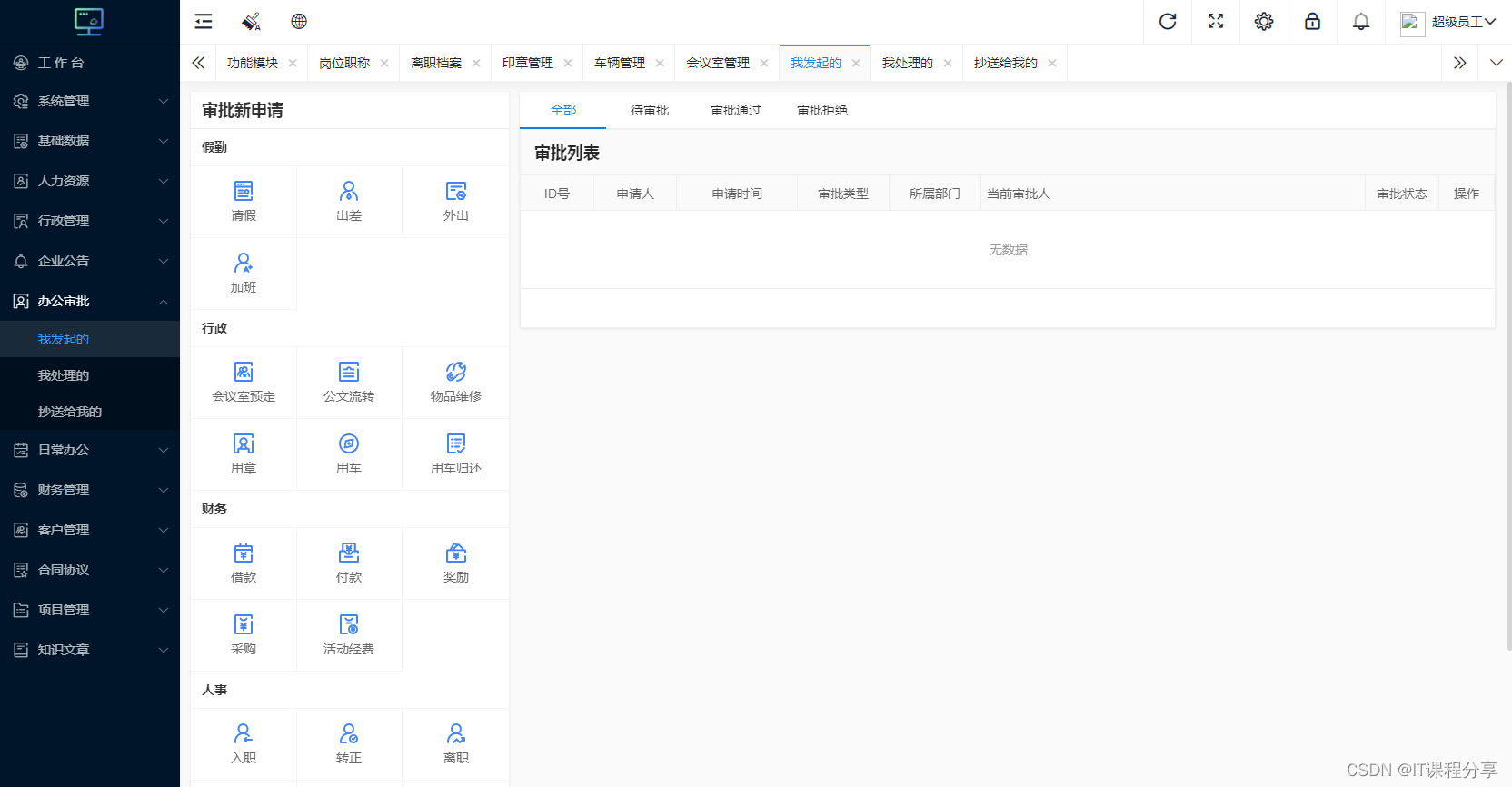
综合OA管理系统源码 OA系统源码
综合OA管理系统源码 OA系统源码 功能介绍: 编号:LQ10 一:系统管理 系统配置,功能模块,功能节点,权限角色,操作日志,备份数据,还原数据 二:基础数据 审批…...
)
9-MySQL提高数据管理效率(分库分表实践)
MySQL提高数据管理效率(分库分表实践) 在当今的互联网时代,随着业务规模的不断扩大,数据量也呈现出爆炸性的增长。如何有效地管理和存储这些数据,以及提高数据库的性能和可扩展性,成为了一个迫切需要解决的…...
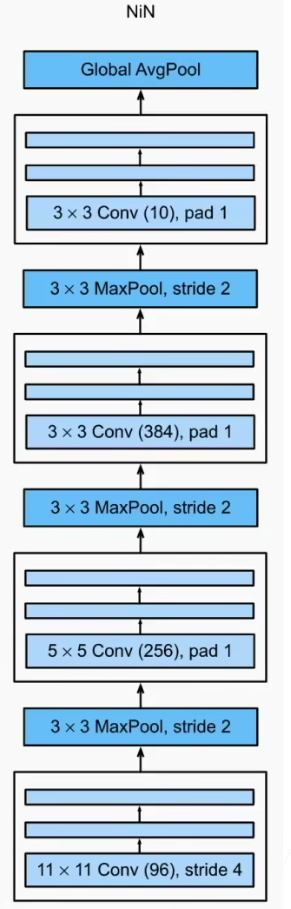
经典卷积神经网络 - NIN
网络中的网络,NIN。 AlexNet和VGG都是先由卷积层构成的模块充分抽取空间特征,再由全连接层构成的模块来输出分类结果。但是其中的全连接层的参数量过于巨大,因此NiN提出用1*1卷积代替全连接层,串联多个由卷积层和“全连接”层构成…...

leetcode_2558 从数量最多的堆取走礼物
1. 题意 给定一个数组,每次从中取走最大的数,返回开根号向下取整送入堆中,最后计算总和。 从数量最多的堆取走礼物 2. 题解 直接用堆模拟即可 2.1 我的代码 用了额外的空间O( n ) priority_queue会自动调用make_heap() 、pop_heap() c…...

01. 嵌入式与人工智能是如何结合的?
CPU是Arm A57的 GPU是128cuda核 一.小车跟踪的需求和设计方法 比如有一个小车跟踪的项目。 需求是:小车识别出罪犯,然后去跟踪他。方法:摄像头采集到人之后传入到开发板,内部做一下识别,然后控制小车去跟随。在人工智…...
vue3.0运行npm run dev 报错Cannot find module node:url
vue3.0运行npm run dev 报错Cannot find module 问题背景 近期用vue3.0写项目,npm init vuelatest —> npm install 都正常,npm run dev的时候报错如下: failed to load config from F:\code\testVue\vue-demo\vite.config.js error when starting…...

26. 删除排序数组中的重复项、Leetcode的Python实现
博客主页:🏆看看是李XX还是李歘歘 🏆 🌺每天分享一些包括但不限于计算机基础、算法等相关的知识点🌺 💗点关注不迷路,总有一些📖知识点📖是你想要的💗 ⛽️今…...

荣耀推送服务消息分类标准
前言 为了提升终端用户的推送体验、营造良好可持续的通知生态,荣耀推送服务将对推送消息进行分类管理。 消息分类 定义 荣耀推送服务将根据应用类型、消息内容和消息发送场景,将推送消息分成服务通讯和资讯营销两大类别。 服务通讯类,包…...
[数据结构]-二叉搜索树
前言 作者:小蜗牛向前冲 名言:我可以接受失败,但我不能接受放弃 如果觉的博主的文章还不错的话,还请点赞,收藏,关注👀支持博主。如果发现有问题的地方欢迎❀大家在评论区指正。 目录 一、二叉搜…...

力扣每日一题79:单词搜索
题目描述: 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格…...

ChatGPT如何应对用户提出的道德伦理困境?
ChatGPT在应对用户提出的道德伦理困境时,需要考虑众多复杂的因素。道德伦理问题涉及到价值观、原则、社会和文化背景,以及众多伦理理论。ChatGPT的设计和应用需要权衡各种考虑因素,以确保它不仅提供有用的信息,而且遵循伦理标准。…...
)
SpringBoot运行流程源码分析------阶段三(Spring Boot外化配置源码解析)
Spring Boot外化配置源码解析 外化配置简介 Spring Boot设计了非常特殊的加载指定属性文件(PropertySouce)的顺序,允许属性值合理的覆盖,属性值会以下面的优先级进行配置。home目录下的Devtool全局设置属性(~/.sprin…...

使用docker在3台服务器上搭建基于redis 6.x的一主两从三台均是哨兵模式
一、环境及版本说明 如果服务器已经安装了docker,则忽略此步骤,如果没有安装,则可以按照一下方式安装: 1. 在线安装(有互联网环境): 请看我这篇文章 传送阵>> 点我查看 2. 离线安装(内网环境):请看我这篇文章 传送阵>> 点我查看 说明:假设每台服务器已…...

手游刚开服就被攻击怎么办?如何防御DDoS?
开服初期是手游最脆弱的阶段,极易成为DDoS攻击的目标。一旦遭遇攻击,可能导致服务器瘫痪、玩家流失,甚至造成巨大经济损失。本文为开发者提供一套简洁有效的应急与防御方案,帮助快速应对并构建长期防护体系。 一、遭遇攻击的紧急应…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

(十)学生端搭建
本次旨在将之前的已完成的部分功能进行拼装到学生端,同时完善学生端的构建。本次工作主要包括: 1.学生端整体界面布局 2.模拟考场与部分个人画像流程的串联 3.整体学生端逻辑 一、学生端 在主界面可以选择自己的用户角色 选择学生则进入学生登录界面…...

黑马Mybatis
Mybatis 表现层:页面展示 业务层:逻辑处理 持久层:持久数据化保存 在这里插入图片描述 Mybatis快速入门 
【HTTP三个基础问题】
面试官您好!HTTP是超文本传输协议,是互联网上客户端和服务器之间传输超文本数据(比如文字、图片、音频、视频等)的核心协议,当前互联网应用最广泛的版本是HTTP1.1,它基于经典的C/S模型,也就是客…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

ABAP设计模式之---“简单设计原则(Simple Design)”
“Simple Design”(简单设计)是软件开发中的一个重要理念,倡导以最简单的方式实现软件功能,以确保代码清晰易懂、易维护,并在项目需求变化时能够快速适应。 其核心目标是避免复杂和过度设计,遵循“让事情保…...

嵌入式学习笔记DAY33(网络编程——TCP)
一、网络架构 C/S (client/server 客户端/服务器):由客户端和服务器端两个部分组成。客户端通常是用户使用的应用程序,负责提供用户界面和交互逻辑 ,接收用户输入,向服务器发送请求,并展示服务…...

【C++进阶篇】智能指针
C内存管理终极指南:智能指针从入门到源码剖析 一. 智能指针1.1 auto_ptr1.2 unique_ptr1.3 shared_ptr1.4 make_shared 二. 原理三. shared_ptr循环引用问题三. 线程安全问题四. 内存泄漏4.1 什么是内存泄漏4.2 危害4.3 避免内存泄漏 五. 最后 一. 智能指针 智能指…...