C语言数据结构之数据结构入门
目录
数据结构介绍
数据结构发展史
何为算法
数据结构基础
基本概念和术语
四大逻辑结构(Logic Structure)
数据类型
理解复杂度概念
时间空间复杂度定义
度量时间复杂度的方法
程序运行时的内存与地址
编程预备
数据结构介绍
数据结构发展史
起源:1968年美国唐•欧•克努特教授开创了数据结构的最初体系,他所著的《计算机程序设计技巧》第一卷《基本算法》是第一本较系统地阐述数据的逻辑结构和存储结构语其操作的著作。我们一般认为本书开创了数据结构的系统概念。70年代初,数据结构作为一门独立的课程开始进入大学课堂。
数据结构的发展经历三个阶段:无结构阶段,结构化阶段和面向对象阶段(和程序发展的三个阶段不谋而合了)
-
无结构阶段:在计算机发展的早期阶段,主要应用于科学计算。此时,程序设计主要使用机器语言和汇编语言,数据的表示和操作主要依赖数学公式和模型。数据结构的概念尚未形成,程序设计更注重数值计算而非数据之间的关系。
-
结构化阶段:随着计算机应用领域的扩大,人们开始关注程序设计规范化的重要性。在这个阶段,数据结构的概念逐渐形成,并引入了抽象数据类型(ADT)的概念。ADT将数据的表示和操作封装在一起,使得程序设计更加模块化和灵活。同时,各种基本的数据结构如数组、链表、栈、队列等得到广泛应用。此时,数据结构的教学和研究也开始兴起。
-
面向对象阶段:80年代初期至今,面向对象的程序设计方法逐渐流行起来。面向对象的设计思想将数据和操作封装在对象中,通过类和继承的机制实现数据结构的抽象和重用。这一阶段,数据结构变得更加丰富多样,大量的封装类如链表、树、图等被设计出来,使得程序设计者能够更方便地使用和操作数据结构。同时,面向对象的设计方法也提供了更好的模块化和可扩展性。
总的来说,数据结构的发展经历了无结构阶段、结构化阶段和面向对象阶段。随着计算机应用领域的扩大和程序设计的不断演进,数据结构的概念逐渐形成并得到广泛应用。这些不同阶段的发展为程序设计者提供了丰富的工具和技术,使得他们能够更好地组织和处理数据,并设计出高效的算法和程序。
何为算法
算法是指解决特定问题的一系列清晰而有限的指令或步骤,这些指令描述了如何在有限时间内完成任务或达成目标。算法可以用来处理各种计算问题,从简单的数学计算到复杂的数据处理和优化任务。
一个算法通常由输入、输出和处理三个部分组成。输入是指问题的初始数据,输出是指解决问题后得到的结果,处理则是指将输入转换为输出的具体步骤。
一个好的算法应该满足以下几个条件:
1. 正确性:算法应该能够正确地解决问题,即产生正确的输出结果。
2. 可读性:算法应该易于理解和阅读,使得其他人能够理解和使用它。
3. 高效性:算法应该在合理的时间内完成任务,即具有高效的时间和空间复杂度。
4. 健壮性:算法应该能够处理各种异常情况,如输入数据的错误或不完整等。
算法在计算机科学中扮演着非常重要的角色,因为它们是计算机程序的核心。无论是编写操作系统、设计网络协议、开发应用程序还是创建游戏,都需要使用算法来实现。因此,学习算法是计算机科学教育中的重要组成部分。
数据结构基础
基本概念和术语
数据:数据是指描述事物的符号或信息。数据不仅仅包括了整形,浮点数等数值类型,还包括了字符甚至声音,视频,图像等非数值的类型。
数据元素:数据元素是数据的基本单位,通常作为一个整体进行处理。例如,一个整数、一个字符或一个对象都可以是一个数据元素。
数据项:数据项是数据元素中的最小单位,它是数据的不可分割的基本单位。例如,一个整数中的每个数字就是一个数据项。
数据对象:是性质相同的一类数据元素的集合,是数据的一个子集。数据对象可以是有限的,也可以是无限的。
数据结构:主要是指数据和关系的集合,数据指的是计算机中需要处理的数据,而关系指的是这些数据相关的前后逻辑,这些逻辑与计算机储存的位置无关,其主要包含以下的四大逻辑结构。
四大逻辑结构(Logic Structure)
1、线性结构:线性结构中的数据元素之间存在一对一的关系,即每个数据元素只有一个直接前驱和一个直接后继。常见的线性结构包括数组、链表、栈和队列。
如图:

2、树形结构:树形结构中的数据元素之间存在一对多的关系,即每个数据元素可以有多个直接后继。常见的树形结构包括二叉树、堆和哈夫曼树。
如图:
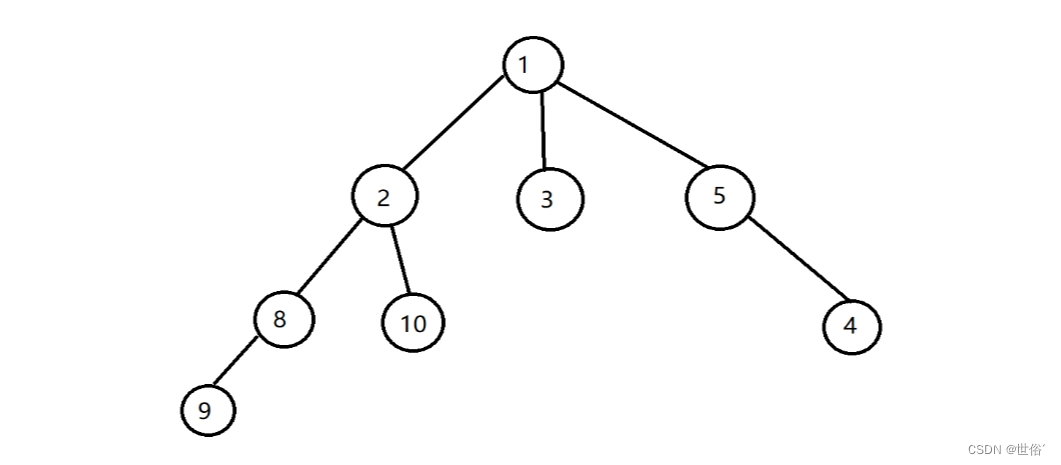
3、图形结构:图形结构中的数据元素之间存在多对多的关系,即每个数据元素可以与多个其他元素相连。常见的图形结构包括有向图和无向图。
如图:
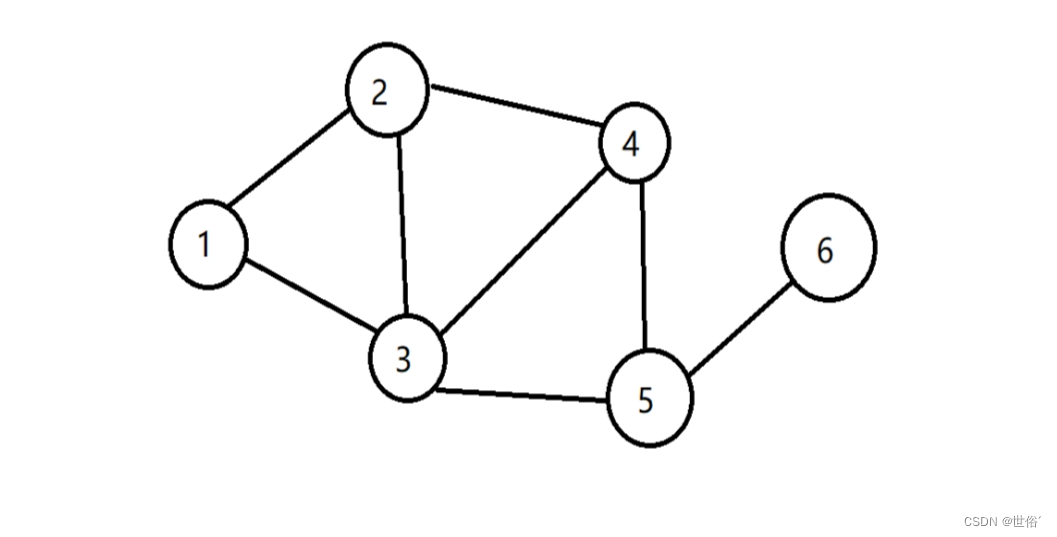
4、集合结构:集合结构中的数据元素之间没有任何特殊的关系,是相互独立的。常见的集合结构包括哈希表和并查集。
如图:

数据类型
1、数据类型
数据类型(Data Type)是高级程序设计语言中的概念,是数据的取值范围和对数进行操作的总和。数据类型规定了程序中对象的特性。程序中的每一个变量,常量或者表达式都属于一种数据类型。
2、抽象数据类型
抽象数据类型是一种概念上的定义,用于描述数据的逻辑结构和操作。它将数据的表示和操作细节隐藏起来,只暴露出对外的接口,使得使用者只需要关注数据的功能而不需要了解具体的实现细节。
抽象数据类型可以看作是一种数据的模板或者蓝图,它定义了数据的取值范围以及对数据进行的操作。通过定义一组操作,可以对数据进行增删改查等操作,而不必关心具体的实现方式。
举个例子,我们可以定义一个抽象数据类型叫做"栈",它可以包含以下操作:
- push:将一个元素压入栈顶
- pop:从栈顶弹出一个元素
- top:获取栈顶元素的值
- isEmpty:判断栈是否为空
- size:获取栈的大小
通过这些操作,我们可以在程序中使用栈这个抽象数据类型来实现各种功能,比如实现括号匹配、逆序输出等。
抽象数据类型的优点在于它提供了高度的封装性和抽象性,使得程序的设计更加模块化和可维护。同时,它也提供了良好的接口定义,使得不同的实现可以替换而不影响使用者的代码。
总之,抽象数据类型是对数据的抽象和封装,定义了数据的取值范围和操作集合,通过隐藏实现细节,提供了高度的模块化和可维护性。它在程序设计中起到了重要的作用,帮助我们更好地组织和管理数据。
理解复杂度概念
时间空间复杂度定义
1、时间复杂度(Time Complexity)是衡量算法执行时间随输入规模增长而增加的度量。它表示算法执行所需的操作次数或时间,通常用大O符号(O)来表示。
时间复杂度描述了算法执行时间与输入规模之间的关系,即算法的运行时间如何随着输入规模的增加而增长。它不是指具体的执行时间,而是一种相对的度量,用于比较不同算法的效率。
常见的时间复杂度有以下几种:
- 常数时间复杂度 O(1):无论输入规模大小,算法的执行时间都保持不变。例如,访问数组中的某个元素。
- 线性时间复杂度 O(n):算法的执行时间与输入规模成线性关系。例如,遍历一个数组。
- 对数时间复杂度 O(log n):算法的执行时间与输入规模的对数成正比。例如,二分查找算法。
- 平方时间复杂度 O(n^2):算法的执行时间与输入规模的平方成正比。例如,嵌套循环遍历一个二维数组。
- 指数时间复杂度 O(2^n):算法的执行时间与输入规模的指数成正比。例如,穷举搜索算法。
综上可以得出:
O(1) < O(logn) < O(n) < O(nlogn) < O(n^2) < O(n^3) < O(2^n)
2、空间复杂度(Space Complexity)是衡量算法所需的额外空间随输入规模增长而增加的度量。它表示算法执行期间所占用的内存空间,通常也用大O符号(O)来表示。
空间复杂度描述了算法所需的额外空间与输入规模之间的关系,即算法的空间使用如何随着输入规模的增加而增长。
常见的空间复杂度有以下几种:
- 常数空间复杂度 O(1):算法所需的额外空间不随输入规模的增加而增加,空间使用保持不变。
- 线性空间复杂度 O(n):算法所需的额外空间与输入规模成线性关系。例如,需要存储一个数组或链表。
- 对数空间复杂度 O(log n):算法所需的额外空间与输入规模的对数成正比。例如,递归算法的调用栈空间。
- 平方空间复杂度 O(n^2):算法所需的额外空间与输入规模的平方成正比。例如,二维数组存储。
需要注意的是,时间复杂度和空间复杂度是相对的概念,它们描述了算法执行时间和空间使用随输入规模变化的趋势,并不是精确的执行时间和空间占用量。在分析算法时,我们通常关注最坏情况下的时间复杂度和空间复杂度,以评估算法的效率和资源消耗。
度量时间复杂度的方法
度量时间复杂度的常用方法是:基于函数调用次数的方法和基于语句执行次数,基于算法复杂度分析的方法。
1、基于函数调用次数的方法: 这种方法通过分析算法中函数或递归调用的次数来度量时间复杂度。它通常适用于递归算法或包含循环结构的算法。具体步骤如下:
- 根据算法的逻辑,确定算法中涉及的函数或递归调用。
- 分析每个函数或递归调用的执行次数与输入规模之间的关系。
- 根据函数调用次数的增长趋势,得出算法的时间复杂度。
例如,对于递归实现的斐波那契数列算法:
int fibonacci(int n) {if (n <= 1)return n;elsereturn fibonacci(n - 1) + fibonacci(n - 2);
}
可以观察到,每次递归调用会导致两次更小规模的递归调用。因此,递归调用次数与输入规模呈指数关系,时间复杂度可以表示为O(2^n)。
2、基于语句执行次数的方法: 这种方法通过分析算法中各个语句的执行次数来度量时间复杂度。它适用于没有函数调用或循环结构的简单算法。具体步骤如下:
- 根据算法的逻辑,确定算法中涉及的各个语句。
- 分析每个语句的执行次数与输入规模之间的关系。
- 根据语句执行次数的增长趋势,得出算法的时间复杂度。
例如,对于以下求和算法:
int sum(int n) {int result = 0;for (int i = 1; i <= n; i++) {result += i;}return result;
}
循环语句的执行次数与输入规模n成线性关系,因此时间复杂度可以表示为O(n)。
3、基于算法复杂度分析:该方法通过分析算法中执行次数最多的语句来度量时间复杂度。通常情况下,算法中执行次数最多的语句是循环语句。因此,我们可以通过分析循环语句的执行次数来确定算法的时间复杂度。
例如,对于以下求幂算法:
double power(double x, int n) {double result = 1.0;for (int i = 0; i < n; i++) {result *= x;}return result;
}
循环语句的执行次数与输入规模n成线性关系,因此时间复杂度可以表示为O(n)。
这三种方法都是常用的度量时间复杂度的方式,选择哪种方法取决于算法的特点和分析的需求。在实际应用中,我们通常使用基于语句执行次数的方法来分析算法的时间复杂度,因为它更直观和简单。但对于一些复杂的递归算法,基于函数调用次数的方法可能更适用。
程序运行时的内存与地址
内存是计算机中用于存储数据和指令的地方,每个内存单元都有一个唯一的地址用于访问其中的数据。通过地址,我们可以直接读取和修改内存中的数据。
在C语言中,指针是一种特殊的变量类型,它存储了一个内存地址。指针的存在使得我们可以通过间接访问内存地址来操作数据,这给编程带来了很大的灵活性。通过指针,我们可以动态分配内存、传递参数、遍历数据结构等。
首先请看这么一张图:
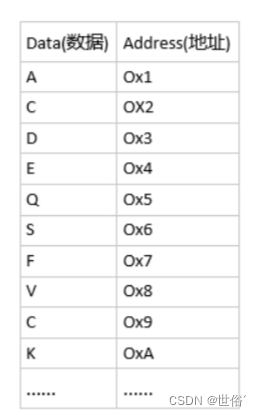
(地址的常用表示为十六进制表示法,即Ox+十六进制数)
由这个图可以清晰的发现对于每一段的内存中的数据,都有一个地址与之相对应,也真是因为有地址的存在,我们计算机中才可以轻易的去访问到其中数据,拿一个数组来说,数组在C语言中是顺序存储的,因此,如上图的数据直接用代码找到其数据以及地址的话可以这样写
#include<stdio.h>
int main(){int i;char array[10]="ACDEQSFVCK";for(i=0;i<10;i++){printf("The %c Address is %x \n",array[i],&array[i]);//%x可以换成%p都是十六进制表示,只不过%p会把所有的位数显示出来}return 0;
}在代码示例中,使用了数组和指针来展示数据在内存中的地址。数组在C语言中是一段连续存储的数据,通过下标可以访问到对应的元素。通过取地址运算符&,我们可以获取数组元素的内存地址。指针变量可以存储这些地址,并通过解引用操作符*来访问或修改该地址处的值。
需要注意的是,不同类型的数据在内存中占用的空间大小是不同的,所以对应的地址也会有所差异。例如,char类型通常占用1字节,而int类型通常占用4字节。因此,当将char数组转换为int数组时,每个元素的地址会相应地增加4个字节。
指针的灵活性和强大功能使其成为C语言的重要特性,但同时也需要小心使用,因为错误的指针操作可能导致内存泄漏、段错误等问题。在编写代码时,应该注意正确地分配和释放内存,并避免悬空指针和越界访问等问题。
编程预备
1、malloc函数是C语言中用于动态分配内存空间的函数,它在堆中申请一块指定大小的连续内存空间,并返回该内存空间的起始地址。malloc函数的原型如下:
void* malloc(size_t size);
其中,size_t是一个无符号整数类型,在stdlib.h头文件中定义。malloc函数接受一个参数size,表示需要分配的内存空间的大小(以字节为单位)。如果内存分配成功,则返回指向分配内存的指针;如果分配失败,则返回空指针NULL。
在使用malloc函数时,需要注意以下几点:
- 在调用malloc函数之后,应该检查返回的指针是否为NULL,以判断内存分配是否成功。如果malloc返回NULL,则表示内存分配失败。
- 分配的内存空间在使用完毕后,应该通过调用free函数来释放,以便将内存返还给系统。否则,会导致内存泄漏问题。
free函数用于释放通过malloc函数分配的内存空间。free函数的原型如下:
void free(void* ptr);
其中,ptr是一个指向待释放内存空间的指针。调用free函数后,该指针所指向的内存空间将被释放,并可以被其他程序重新使用。需要注意的是,ptr必须是通过malloc、calloc或realloc函数返回的指针,或者是空指针NULL。如果ptr不满足这些条件,调用free函数将导致未定义的行为。
在使用free函数时,需要注意以下几点:
- 只能释放通过malloc、calloc或realloc函数分配的内存空间,否则会导致未定义的行为。
- 释放内存后,应该将指针设置为NULL,以避免成为野指针。
总结来说,malloc和free是C语言中用于动态分配和释放内存空间的重要函数。合理地使用这两个函数可以避免内存泄漏和野指针等问题,提高程序的效率和稳定性。
下面是一个使用malloc和free函数的代码示例,用于动态分配一个int类型的数组,并对其进行赋值和释放:
#include <stdio.h>
#include <stdlib.h>int main() {int n = 5; // 数组大小int *arr = (int*) malloc(n * sizeof(int)); // 动态分配内存空间if (arr == NULL) { // 判断内存分配是否成功printf("Memory allocation failed.\n");exit(1);}for (int i = 0; i < n; i++) { // 对数组进行赋值arr[i] = i + 1;}for (int i = 0; i < n; i++) { // 输出数组元素printf("%d ", arr[i]);}printf("\n");free(arr); // 释放内存空间arr = NULL; // 将指针设置为NULL,避免成为野指针return 0;
}
输出结果:
1 2 3 4 5上述代码中,首先定义了一个整型变量n表示数组大小,然后使用malloc函数动态分配了一个大小为n的int类型数组,并将返回的指针赋值给指针变量arr。在分配内存空间之后,需要检查返回的指针是否为NULL,以判断内存分配是否成功。
接着,使用for循环对数组进行赋值,并使用另一个for循环输出数组元素。最后,使用free函数释放arr指向的内存空间,并将指针设置为NULL,以避免成为野指针。
相关文章:

C语言数据结构之数据结构入门
目录 数据结构介绍 数据结构发展史 何为算法 数据结构基础 基本概念和术语 四大逻辑结构(Logic Structure) 数据类型 理解复杂度概念 时间空间复杂度定义 度量时间复杂度的方法 程序运行时的内存与地址 编程预备 数据结构介绍 数据结构发展…...
如何知道服务器的某个端口是否打开
1、telnet 命令:telnet ip port,port即端口,我们一般最常见的命令就是telnet,但是telnet使用的是tcp协议,换句话说telnet只能检测tcp的这个端口打开了没 若是端口打开,会出现下列信息 失败的是这个 如…...

【ICCV‘23】One-shot Implicit Animatable Avatars with Model-based Priors
文章目录 前置知识 前置知识 1)SMPL模型 \quad SMPL这类方法只建模穿很少衣服的人体(裸体模型),它只能刻画裸体角色的动画,并不能刻画穿衣服的人体的动画 2)data-efficient \quad 这个词推荐用ÿ…...
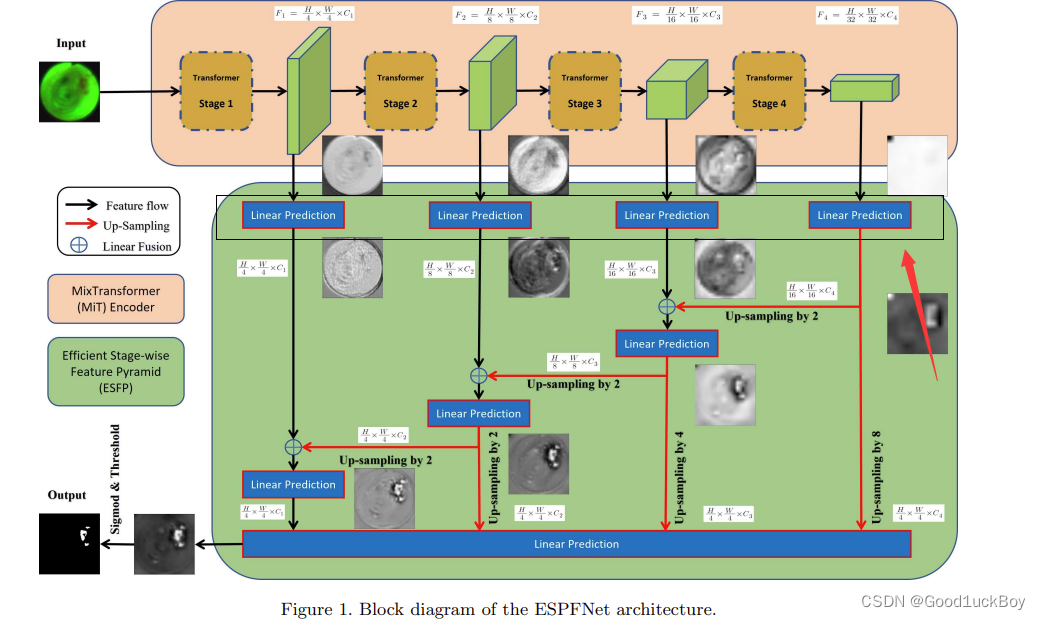
关于息肉检测和识别项目的总结
前言 整体的思路:首先息肉数据集分为三类: 1.正常细胞 2. 增生性息肉 3. 肿瘤要想完成这个任务,首先重中之重是分割任务,分割结果的好坏, 当分割结果达到一定的准确度后,开始对分割后的结果进行下游分类…...

Jetson Xavier NX FFmpeg支持硬件编解码
最近在用Jetson Xavier NX板子做视频处理,但是CPU进行视频编解码,效率比较地下。 于是便考虑用硬解码来对视频进行处理。 通过jtop查看,发现板子是支持 NVENC硬件编解码的。 1、下载源码 因为需要对ffmpeg进行打补丁修改,因此需要编译两份源码 1.1、编译jetson-ffmpeg …...

518抽奖软件,为什么说比别的抽奖软件更美观精美?
518抽奖软件简介 518抽奖软件,518我要发,超好用的年会抽奖软件,简约设计风格。 包含文字号码抽奖、照片抽奖两种模式,支持姓名抽奖、号码抽奖、数字抽奖、照片抽奖。(www.518cj.net) 精致美观功能 字体平滑无锯齿图片放大后清晰…...

React的组件学习
React的组件学习 参考资料:https://zh-hans.react.dev/learn/your-first-component 一、定义组件 export default function Profile() {return (<imgsrc"https://i.imgur.com/MK3eW3Am.jpg"alt"Katherine Johnson"/>) }以下是构建组件…...
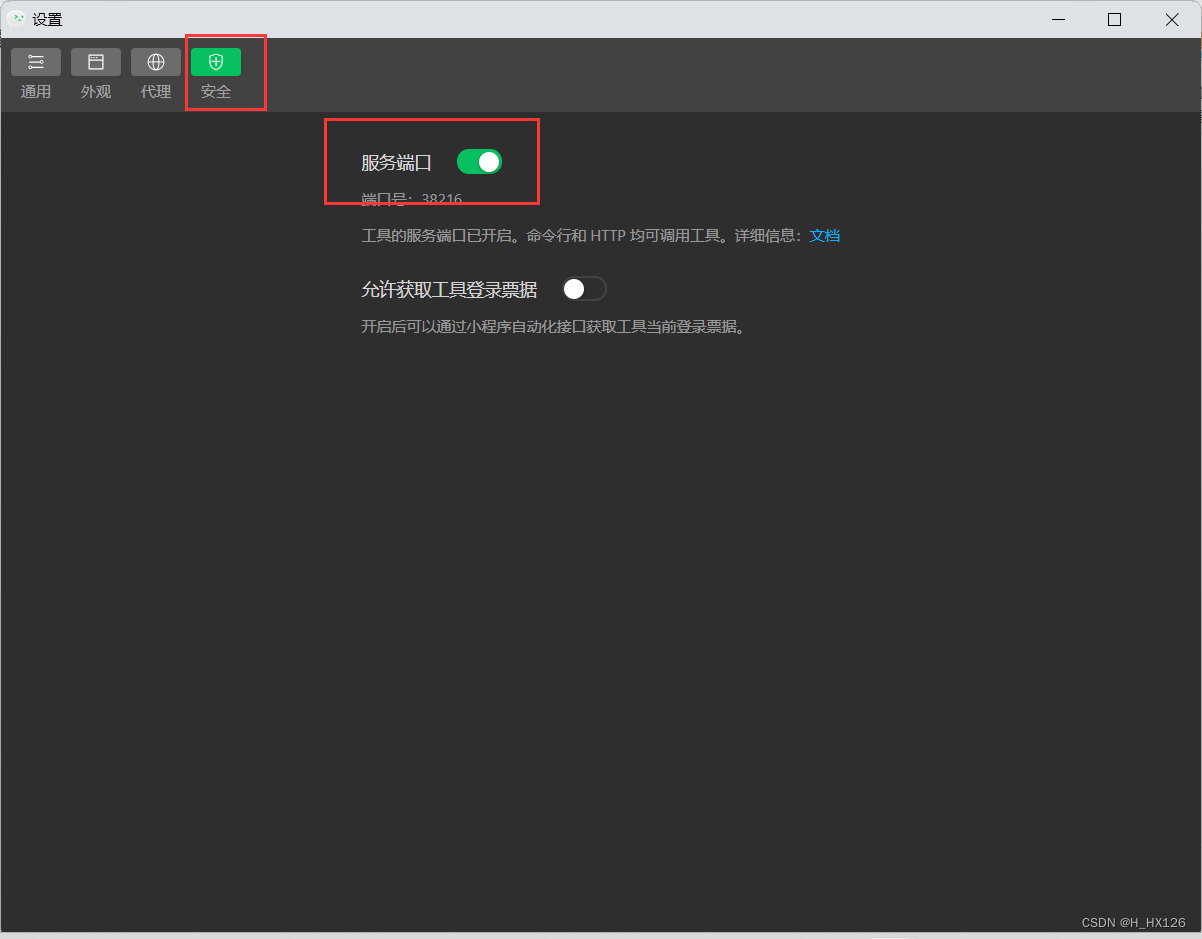
uni-app配置微信开发者工具
一、配置微信开发者工具路径 工具->设置->运行配置->小程序运行配置->微信开发者工具路径 二、微信开发者工具开启服务端口...
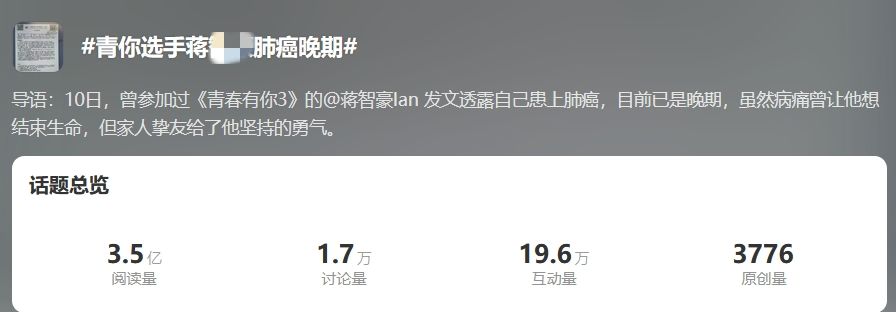
肺癌不再是老年病:33岁作家的离世引发关注,有这些情况的请注意
近期,90后网络小说家七月新番和26岁男艺人蒋某某因肺癌去世,引发关注。他们都没有吸烟习惯,那么他们为什么会得肺癌呢?浙大二院呼吸内科副主任医师兰芬说,现在年轻人熬夜、加班导致身体过劳,在劳累情况下身…...

【兔子王赠书第4期】用ChatGPT轻松玩转机器学习与深度学习
文章目录 前言机器学习深度学习ChatGPT推荐图书粉丝福利尾声 前言 兔子王免费赠书第4期来啦,突破传统学习束缚,借助ChatGPT的神奇力量,解锁AI无限可能! 机器学习 机器学习是人工智能领域的一个重要分支,它的目的是让…...
(转载))
Ubuntu18.04 ROS Melodic的cv_bridge指向问题(四种方式,包括opencv4)(转载)
转载自: 【精选】Ubuntu18.04 ROS Melodic的cv_bridge指向问题(四种方式,包括opencv4)_XiangrongZ的博客-CSDN博客...
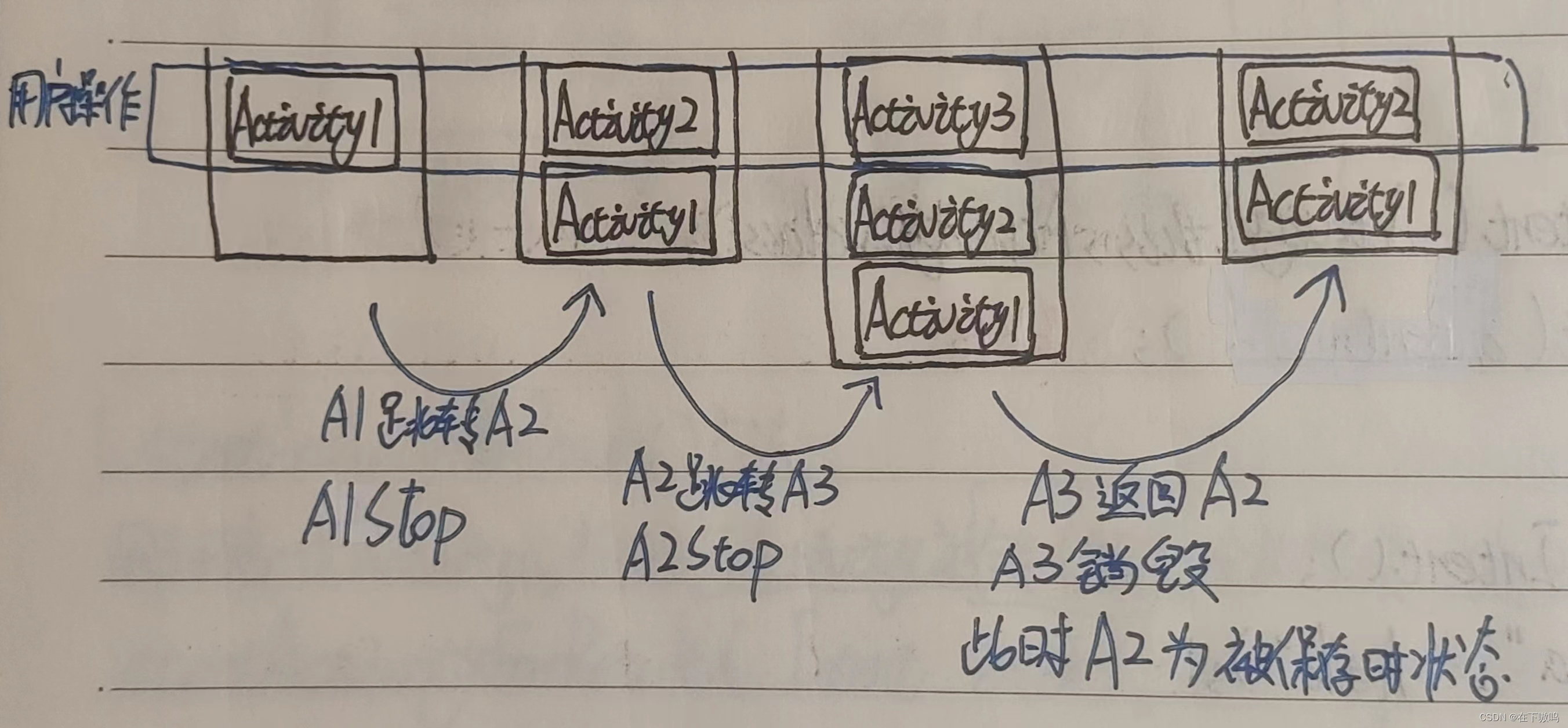
Android任务栈和启动模式
Andrcid中的任务栈是一种用来存放Activity实倒的容器。任务最大的特点就是先进后出,它主要有两个基本操作,分别是压栈和出栈。通常Andaid应用程序都有一个任务栈,每打开一个Activity时,该Activity就会被压入任务栈。每销毁一个Act…...
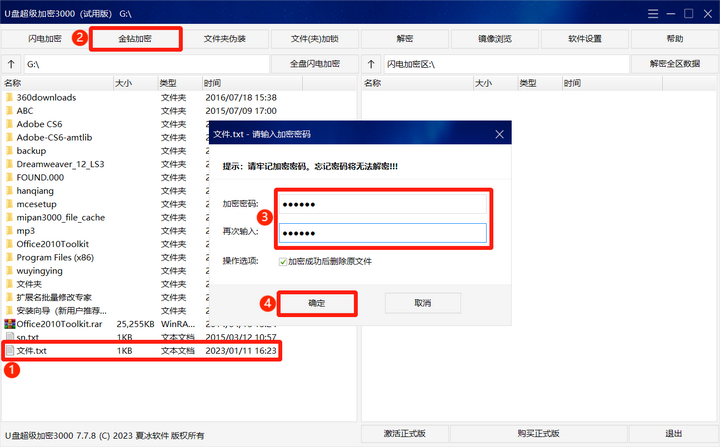
电脑加密软件哪个好?电脑加密软件推荐
电脑是我们办公离不开的工具,而为了保护电脑数据安全,我们可以使用专业的电脑加密软件来进行加密保护。那么,电脑加密软件哪个好呢?下面我们就来了解一下。 文件加密——超级加密3000 想要安全加密电脑重要文件,我们可…...

如何优雅地单元测试 Kotlin/Java 中的 private 方法?
翻译自 https://medium.com/mindorks/how-to-unit-test-private-methods-in-java-and-kotlin-d3cae49dccd ❓如何单元测试 Kotlin/Java 中的 private 方法❓ 首先,开发者应该测试代码里的 private 私有方法吗? 直接信任这些私有方法,测试到…...

单元测试,集成测试,系统测试的区别是什么?
实际的测试工作当中,我们会从不同的角度对软件测试的活动进行分类,题主说的“单元测试,集成测试,系统测试”,是按照开发阶段进行测试活动的划分。这种划分完整的分类,其实是分为四种“单元测试,…...
第十八节 串(KMP算法))
数据结构(超详细讲解!!)第十八节 串(KMP算法)
1.BF算法 算法在字符比较不相等,需要回溯(即ii-j1):即退到s中的下一个字符开始进行继续匹配。 最好情况下的时间复杂度为O(m)。 最坏情况下的时间复杂度为O(nm)。 平均的时间复杂度为O(nm)。 2.KMP算法 KMP算法是D.E.Knuth、…...

软考_软件设计师
算法: 1、直接插入排序 详解:https://blog.csdn.net/qq_44616044/article/details/115708056 void insertSort(int data[],int n){int i,j,temp;for(i1;i<n;i){if(data[i]<data[i-1]){temp data[i];data[i] data[i-1];for(ji-1;j>0&&am…...

大数据之LibrA数据库系统告警处理(ALM-12004 OLdap资源异常)
告警解释 当Manager中的Ldap资源异常时,系统产生此告警。 当Manager中的Ldap资源恢复,且告警处理完成时,告警恢复。 告警属性 告警参数 对系统的影响 Ldap资源异常,Manager和组件WebUI认证服务不可用,无法对Web上层…...
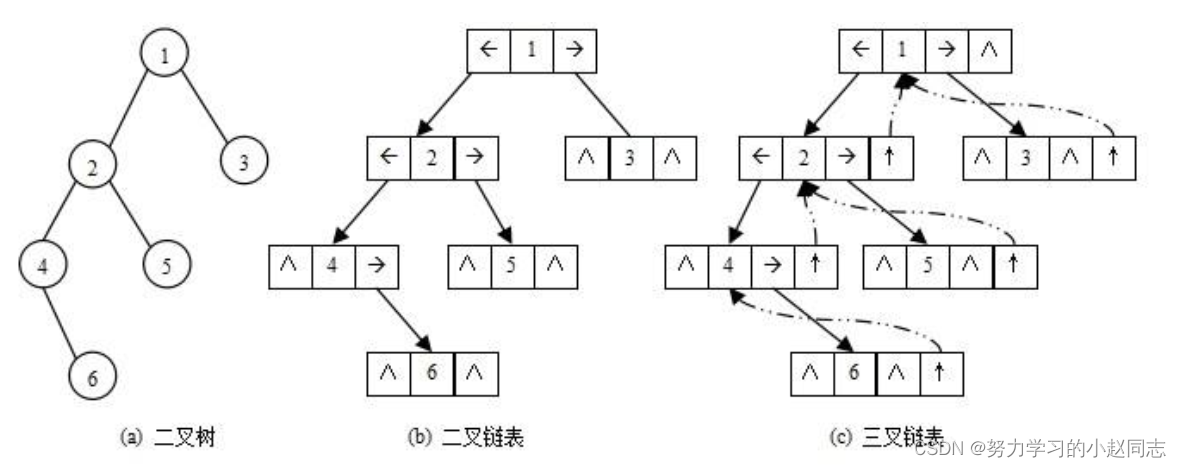
详解—数据结构《树和二叉树》
目录 一.树概念及结构 1.1树的概念 1.2树的表示 二.二叉树的概念及结构 2.1概念 2.2二叉树的特点 2.3现实中的二叉树 2.4数据结构中的二叉树 2.5 特殊的二叉树 2.6二叉树的存储结构 2.6.1二叉树的性质 2.6.2 顺序结构 2.6.3链式存储 三. 二叉树的链式结构的遍历 …...
菜单管理中icon图标回显
<el-table-column prop"icon" label"图标" show-overflow-tooltip algin"center"><template v-slot"{ row }"><el-icon :class"row.icon"></el-icon></template></el-table-column>...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

mongodb源码分析session执行handleRequest命令find过程
mongo/transport/service_state_machine.cpp已经分析startSession创建ASIOSession过程,并且验证connection是否超过限制ASIOSession和connection是循环接受客户端命令,把数据流转换成Message,状态转变流程是:State::Created 》 St…...

解锁数据库简洁之道:FastAPI与SQLModel实战指南
在构建现代Web应用程序时,与数据库的交互无疑是核心环节。虽然传统的数据库操作方式(如直接编写SQL语句与psycopg2交互)赋予了我们精细的控制权,但在面对日益复杂的业务逻辑和快速迭代的需求时,这种方式的开发效率和可…...

定时器任务——若依源码分析
分析util包下面的工具类schedule utils: ScheduleUtils 是若依中用于与 Quartz 框架交互的工具类,封装了定时任务的 创建、更新、暂停、删除等核心逻辑。 createScheduleJob createScheduleJob 用于将任务注册到 Quartz,先构建任务的 JobD…...

均衡后的SNRSINR
本文主要摘自参考文献中的前两篇,相关文献中经常会出现MIMO检测后的SINR不过一直没有找到相关数学推到过程,其中文献[1]中给出了相关原理在此仅做记录。 1. 系统模型 复信道模型 n t n_t nt 根发送天线, n r n_r nr 根接收天线的 MIMO 系…...

《C++ 模板》
目录 函数模板 类模板 非类型模板参数 模板特化 函数模板特化 类模板的特化 模板,就像一个模具,里面可以将不同类型的材料做成一个形状,其分为函数模板和类模板。 函数模板 函数模板可以简化函数重载的代码。格式:templa…...

动态 Web 开发技术入门篇
一、HTTP 协议核心 1.1 HTTP 基础 协议全称 :HyperText Transfer Protocol(超文本传输协议) 默认端口 :HTTP 使用 80 端口,HTTPS 使用 443 端口。 请求方法 : GET :用于获取资源,…...

Linux nano命令的基本使用
参考资料 GNU nanoを使いこなすnano基础 目录 一. 简介二. 文件打开2.1 普通方式打开文件2.2 只读方式打开文件 三. 文件查看3.1 打开文件时,显示行号3.2 翻页查看 四. 文件编辑4.1 Ctrl K 复制 和 Ctrl U 粘贴4.2 Alt/Esc U 撤回 五. 文件保存与退出5.1 Ctrl …...

为什么要创建 Vue 实例
核心原因:Vue 需要一个「控制中心」来驱动整个应用 你可以把 Vue 实例想象成你应用的**「大脑」或「引擎」。它负责协调模板、数据、逻辑和行为,将它们变成一个活的、可交互的应用**。没有这个实例,你的代码只是一堆静态的 HTML、JavaScript 变量和函数,无法「活」起来。 …...
