当前位置：首页 > news >正文

线性代数第四章线性方程组

news 2025/10/20 3:48:26

一、矩阵形式

$Ax=b,Ax=0$

经过初等行变换化为阶梯形矩阵。当 $r(A)=r(\bar{A})$ ，有解；当 $r(A)< n$ ，有非零解。

$Ax=b$ 有解，等价于

$\beta$ 可由 $\alpha _1,\alpha _2,...,\alpha _n$ 线性表示
$r(\alpha _1,\alpha _2,...,\alpha _n)=r(\alpha _1,\alpha _2,...,\alpha _n,\beta )$

克拉默法则：非齐次线性方程组中，系数行列式 $\left | A \right |\neq 0$ ，则方程组有唯一解，且唯一解为 $x_i=\frac{\left | A_i \right |}{\left | A \right |},i=1,2,...,n.$

其中 $\left | A_i \right |$ 是 $\left | A \right |$ 中第i列元素（即 $x_i$ 的系数）替换成方程组右端的常数项 $b_1,b_2,...b_n$ 所构成的行列式。

二、向量形式

$x_1\alpha _1+x_2\alpha _2+...+x_n\alpha _n=\beta$ 方程组有解等价于 $\beta$ 可由 $\alpha _1,\alpha _2,...,\alpha _n$ 表出；

$x_1\alpha _1+x_2\alpha _2+...+x_n\alpha _n=0$ 方程组有非零解等价于 $\alpha _1,\alpha _2,...,\alpha _n$ 线性相关。

三、齐次线性方程组

若A是 $m\times n$ 矩阵， $r(A)=r<n$ ，则齐次线性方程组 $Ax=0$ 存在基础解系，且基础解系有 $n-r$ 个线性无关解向量组成。也就是说，基础解系向量个数+ $r(A)$ =n（未知量个数）。

四、非齐次线性方程组

$Ax=b$ 有解条件

（1） $A_{m\times n}x=b$ 无解，等价于

b不能由A的列向量组 $\alpha _1,\alpha _2,...,\alpha _n$ 线性表出
$r(A)\neq r(A\mid b),(r(A)+1= r(A\mid b))$

（2） $A_{m\times n}x=b$ 有解，等价于

b可由A的列向量组 $\alpha _1,\alpha _2,...,\alpha _n$ 线性表出
$r(A)=r(A\mid b)$ ，即 $r(\alpha _1,\alpha _2,...,\alpha _n)=r(\alpha _1,\alpha _2,...,\alpha _n,b)$
$(\alpha _1,\alpha _2,...,\alpha _n)\cong (\alpha _1,\alpha _2,...,\alpha _n,b)$

若 $r(\alpha _1,\alpha _2,...,\alpha _n)=r(\alpha _1,\alpha _2,...,\alpha _n,b)=n$ $\Leftrightarrow$ $\alpha _1,\alpha _2,...,\alpha _n$ 线性无关， $\alpha _1,\alpha _2,...,\alpha _n,b$ 线性相关 $\Leftrightarrow$ b可由 $\alpha _1,\alpha _2,...,\alpha _n$ 线性表出，且表出法唯一 $\Leftrightarrow Ax=b$ 有唯一解。

若 $r(\alpha _1,\alpha _2,...,\alpha _n)=r(\alpha _1,\alpha _2,...,\alpha _n,b)<n$ $\Leftrightarrow$ $\alpha _1,\alpha _2,...,\alpha _n$ 线性无关， $\alpha _1,\alpha _2,...,\alpha _n,b$ 线性相关 $\Leftrightarrow$ b可由 $\alpha _1,\alpha _2,...,\alpha _n$ 线性表出，且表出法不唯一 $\Leftrightarrow Ax=b$ 有无穷多解。

五、解的性质

若 $\alpha _1,\alpha _2$ 是 $Ax=b$ 的解，则 $\alpha _1-\alpha _2$ 是 $Ax=0$ 的解；

若 $\eta _1,\eta _2$ 是 $Ax=0$ 的解，则 $k_1\eta _1+k_2\eta _2$ 是 $Ax=0$ 的解；

若 $\alpha$ 是 $Ax=b$ 的解， $\eta$ 是 $Ax=0$ 的解，则 $\alpha +\eta$ 是 $Ax=b$ 的解。

六、解的结构

特解，通解，自由变量。

如果有方程组就加减消元、讨论参数，求解；

如果没有方程组就大概需求秩，用解的结构来分析推理来求解。

线性代数第四章线性方程组

一、矩阵形式

$Ax=b,Ax=0$

二、向量形式

三、齐次线性方程组

四、非齐次线性方程组

五、解的性质

六、解的结构

相关文章：

线性代数第四章线性方程组

@DateTimeFormat和@JsonFormat注解

做抖音短视频会经历哪些阶段？

【Mquant】2、量化平台的选择

iPhone手机如何恢复删除的视频？整理了3个好用方法！

全网最全的RDMA拥塞控制入门基础教程

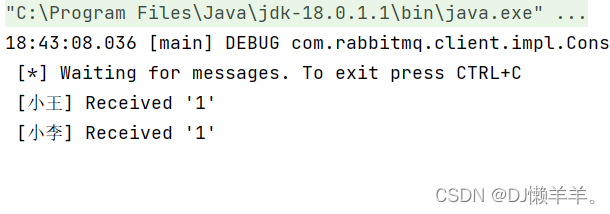
分布式消息队列:RabbitMQ(1)

Redis集群脑裂

GEE教程——随机样本点添加经纬度信息

PyTorch入门学习（十）：神经网络-非线性激活

《golang设计模式》第三部分·行为型模式-03-解释器模式（Interpreter）

Windows个性化颜色睡眠后经常改变

calico ipam使用

Redis系统学习（高级篇）-Redis持久化-AOF方式

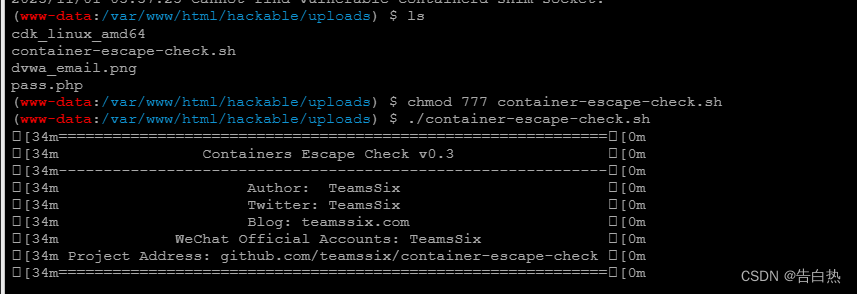
云安全-云原生基于容器漏洞的逃逸自动化手法（CDK check）

精选10款Python可视化工具，请查收

大数据(21)-skew-GroupBy

window压缩包安装mongodb并注册系统服务

【Java每日一题】——第四十五题：综合案例：模拟物流快递系统。（2023.11.1）

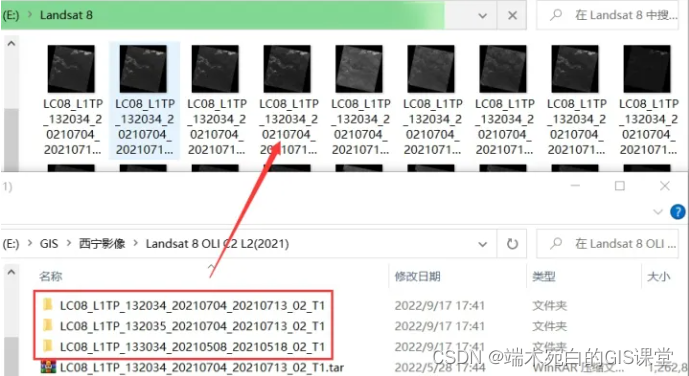
二十二、Arcpy批量波段组合——结合Landat数据城市建成区提取

【杂谈】-递归进化：人工智能的自我改进与监管挑战

连锁超市冷库节能解决方案：如何实现超市降本增效

Caliper 配置文件解析：config.yaml

视觉slam十四讲实践部分记录——ch2、ch3

AirSim/Cosys-AirSim 游戏开发（四）外部固定位置监控相机

R 语言科研绘图第 55 期 --- 网络图-聚类

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧

前端工具库lodash与lodash-es区别详解

react更新页面数据，操作页面，双向数据绑定

Web APIS Day01