⌈C++11⌋实现一个简易计算器
原理:
数据栈:有数据就直接入栈
运算符栈:设遍历到当前的运算符位e,如果栈不为空,比较栈顶与当前运算符优先级e,当栈顶运算符优先级大于或者等于e的优先级,则出栈,并将两个数据栈的数据出栈,计算出对应的数据,加入到数据栈中,否则将运算符入栈
#include <iostream>
#include <unordered_map>
#include <stack>
#include <functional>
#include <string>#define MAX_PRI INT_MAXusing namespace std;
int main() {//数据栈stack<double> _data; //运算符栈stack<char> _operator; //运算符优先级unordered_map<char, int> pri{ {'+', 0}, {'-', 0}, {'*', 1}, {'/', 1}, {'^', 2}, {'(', MAX_PRI }, {')', MAX_PRI}};unordered_map<char, function<double(double, double)>> func{{'+', [](double x, double y) -> double { return x + y; }},{'-', [](double x, double y) -> double { return x - y; }}, {'*', [](double x, double y) -> double { return x * y; }},{'/', [](double x, double y) -> double { return x / y; }},{'^', [](double x, double y) -> double { return pow(x, y); }}};string exp;cin >> exp;auto calculate = [&_data, &_operator, &func]() {char op = _operator.top();_operator.pop();double x = _data.top();_data.pop();double y = _data.top();_data.pop();_data.push(func[op](y, x)); //运算顺序与出栈顺序相反};auto stringtonum = [&exp, &pri](int& i) -> double {int j = i + 1;while (j < exp.length() && pri.find(exp[j]) == pri.end()) j++;double num = stod(exp.substr(i, j - i));i = j - 1; return num;};for (int i = 0; i < exp.length(); ++i) {char e = exp[i];if (pri.find(e) == pri.end()) { //当前字符不是运算符,则切割数字_data.push(stringtonum(i));} else if (e == '(') {_operator.push('(');} else if (e == ')') {while (_operator.top() != '(') {calculate();}_operator.pop();} else {//当前运算符优先级<=栈顶运算符优先级,则出栈计算while (!_operator.empty() && pri[_operator.top()] >= pri[e] && _operator.top() != '(') {calculate();}_operator.push(e);}}while (!_operator.empty()) {calculate();}cout << _data.top() << endl;
}相关文章:

⌈C++11⌋实现一个简易计算器
原理: 数据栈:有数据就直接入栈 运算符栈:设遍历到当前的运算符位e,如果栈不为空,比较栈顶与当前运算符优先级e,当栈顶运算符优先级大于或者等于e的优先级,则出栈,并将两个数据栈的…...
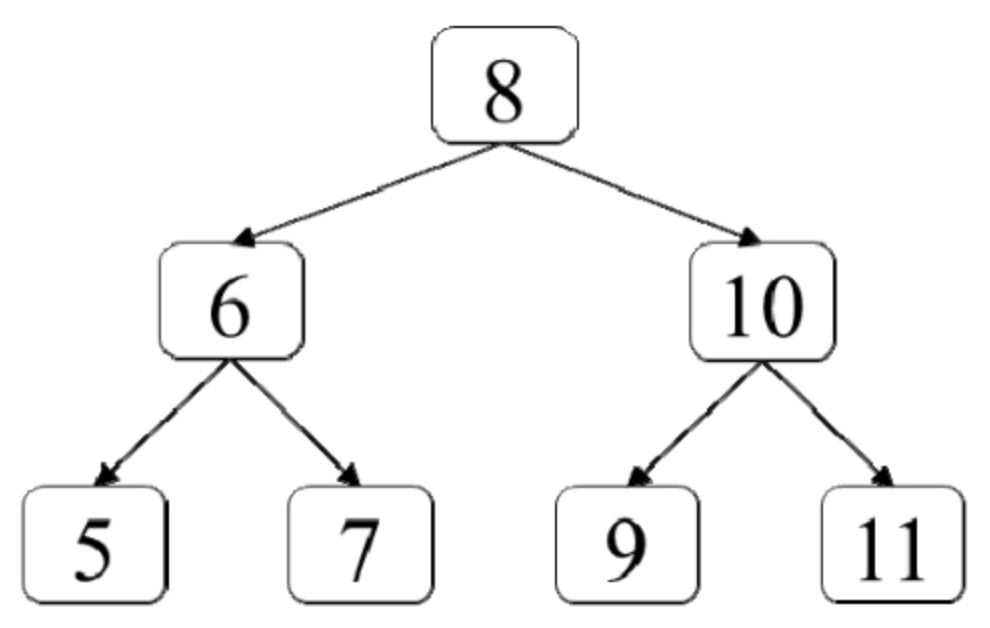
面试算法45:二叉树最低层最左边的值
题目 如何在一棵二叉树中找出它最低层最左边节点的值?假设二叉树中最少有一个节点。例如,在如图7.5所示的二叉树中最低层最左边一个节点的值是5。 分析 可以用一个变量bottomLeft来保存每一层最左边的节点的值。在遍历二叉树时,每当遇到新…...

Could not find org.jetbrains.kotlin:kotlin-stdlib-jre7:1.5.21.
前两天下了一个demo,运行时候报了一个这样的错,特此记录一下。 先看下报的错。 Caused by: org.gradle.internal.resolve.ModuleVersionNotFoundException: Could not find org.jetbrains.kotlin:kotlin-stdlib-jre7:1.5.21. Searched in the following…...

LoRaWan之LoRaMAC 的快速入门指南
概述 本快速入门指南简要介绍了 LoRaMAC 层的重要操作。示例部分提供了不同设备类别的完整示例。 初始化 LoRaMAC层的初始化函数是LoRaMacInitialization( LoRaMacPrimitives_t *primitives, LoRaMacCallback_t *callbacks, LoRaMacRegion_t region )。该函数具有三个参数:L…...

中国教育企业出海 新兴技术助力抢占先机
继游戏、电商、短视频等领域轮番出海之后,国内教育企业纷纷开启了出海之路。近日发布的《2023年教育应用出海市场洞察》报告显示,在中国教育企业出海市场中,语言学习是最主要的赛道,但赛道竞争更为激烈。 报告指出,全…...

IntelliJ IDEA2023旗舰版和社区版下载安装教程(图解)
🌷🍁 博主猫头虎 带您 Go to New World.✨🍁 🦄 博客首页——猫头虎的博客🎐 🐳《面试题大全专栏》 文章图文并茂🦕生动形象🦖简单易学!欢迎大家来踩踩~🌺 &a…...

【RxJava】map过程中各个Observable生命周期分析
map和flatMap的区别 首先说下map和flatMap的区别,防止有对RxJava还不够熟悉的小伙伴 map的Function指定如何将A转为BflatMap的Function则指定如何将Observable<A>转为Observable<B>map和flatMap最终的转换结果都是Observable<B>flatMap由于可以…...

vue 获取上一周和获取下一周的日期时间
效果图: 代码 <template><div><div style"padding: 20px 0;"><div style"margin-left: 10px; border-left: 5px solid #0079fe; font-size: 22px; font-weight: 600; padding-left: 10px">工作计划</div><di…...
线性代数 第四章 线性方程组
一、矩阵形式 经过初等行变换化为阶梯形矩阵。当,有解;当,有非零解。 有解,等价于 可由线性表示 克拉默法则:非齐次线性方程组中,系数行列式,则方程组有唯一解,且唯一解为 其中是…...

@DateTimeFormat和@JsonFormat注解
在日常开发中,有用到时间类型作为查询参数或者查询结果有时间参数的一般都会见过这两个注解。 DateTimeFormat(pattern “yyyy-MM-dd HH:mm:ss”)注解用于解析请求接口入参。将入参的字符串按照pattern设置的格式来转换成日期时间对象。 JsonFormat(timezone “G…...

做抖音短视频会经历哪些阶段?
今天来聊聊那些在抖音做大的老板,从开始到后期经历的四个阶段,以及每个阶段的工作重心 1、0—1的阶段 0—1的起步阶段是整个阶段最有难度的一环,很多人对0到1的认知是有错误的,以为爆过几条视频就已经进阶了 想要实现0-1的突破…...

【Mquant】2、量化平台的选择
文章目录 一、选择因素二、常见的量化平台三、为什么选择VeighNa?四、参考 一、选择因素 功能和工具集:量化平台应该提供丰富的功能和工具集,包括数据分析、策略回测、实时交易等。不同的平台可能有不同的特点和优势,可以根据自己…...
iPhone手机如何恢复删除的视频?整理了3个好用方法!
在日常生活中,我们会把各种各样的视频存放在手机里。这些视频记录着我们生活中的点点滴滴,每一帧都承载着珍贵的记忆。但如果我们不小心将这些重要视频删除了该怎么办?如何恢复删除的视频?本文将以iPhone手机为例子,教…...

全网最全的RDMA拥塞控制入门基础教程
RDMA-CC(全网最全的RDMA拥塞控制入门基础教程) 文章目录 RDMA-CC(全网最全的RDMA拥塞控制入门基础教程)DMARDMARDMA举例RDMA优势RDMA的硬件实现方法RDMA基本术语FabricCA(Channel Adapter)Verbs 核心概念Me…...
分布式消息队列:RabbitMQ(1)
目录 一:中间件 二:分布式消息队列 2.1:是消息队列 2.1.1:消息队列的优势 2.1.1.1:异步处理化 2.1.1.2:削峰填谷 2.2:分布式消息队列 2.2.1:分布式消息队列的优势 2.2.1.1:数据的持久化 2.2.1.2:可扩展性 2.2.1.3:应用解耦 2.2.1.4:发送订阅 2.2.2:分布式消息队列…...

Redis集群脑裂
1. 概述 Redis 集群脑裂(Cluster Split Brain)是指在 Redis 集群中,由于网络分区或通信问题,导致集群中的节点无法相互通信,最终导致集群内部发生分裂,出现多个子集群,每个子集群认为自己是有效…...

GEE教程——随机样本点添加经纬度信息
简介: 有没有办法在绘制散点图后将样本的坐标信息(纬度/经度)添加到.CSV表格数据中? 这里我们很多时候我们需要加载样本点的基本信息作为属性,本教程主要的目的就是我们选取一个研究区,然后产生随机样本点,然后利用坐标函数,进行样本点的获取经纬度,然后通过循环注意…...
:神经网络-非线性激活)
PyTorch入门学习(十):神经网络-非线性激活
目录 一、简介 二、常见的非线性激活函数 三、实现非线性激活函数 四、示例:应用非线性激活函数 一、简介 在神经网络中,激活函数的主要目的是引入非线性特性,从而使网络能够对非线性数据建模。如果只使用线性变换,那么整个神…...
)
《golang设计模式》第三部分·行为型模式-03-解释器模式(Interpreter)
文章目录 1. 概述1.1 角色1.2 类图1.3 优缺点 2. 代码示例2.1 设计2.2 代码2.3 类图 1. 概述 解释器模式(Interpreter)是用于表达语言语法树和封装语句解释(或运算)行为的对象。 1.1 角色 AbstractExpression(抽象表…...

Windows个性化颜色睡眠后经常改变
问题再现 我把系统颜色换成了一种红色,结果每次再打开电脑又变回去了(绿色); 原因是因为wallpaper engine在捣蛋 需要禁用修改windows配色这一块选项; 完事!原来是wallpaper engine的问题;...

UE5 学习系列(二)用户操作界面及介绍
这篇博客是 UE5 学习系列博客的第二篇,在第一篇的基础上展开这篇内容。博客参考的 B 站视频资料和第一篇的链接如下: 【Note】:如果你已经完成安装等操作,可以只执行第一篇博客中 2. 新建一个空白游戏项目 章节操作,重…...

五年级数学知识边界总结思考-下册
目录 一、背景二、过程1.观察物体小学五年级下册“观察物体”知识点详解:由来、作用与意义**一、知识点核心内容****二、知识点的由来:从生活实践到数学抽象****三、知识的作用:解决实际问题的工具****四、学习的意义:培养核心素养…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

TRS收益互换:跨境资本流动的金融创新工具与系统化解决方案
一、TRS收益互换的本质与业务逻辑 (一)概念解析 TRS(Total Return Swap)收益互换是一种金融衍生工具,指交易双方约定在未来一定期限内,基于特定资产或指数的表现进行现金流交换的协议。其核心特征包括&am…...

leetcodeSQL解题:3564. 季节性销售分析
leetcodeSQL解题:3564. 季节性销售分析 题目: 表:sales ---------------------- | Column Name | Type | ---------------------- | sale_id | int | | product_id | int | | sale_date | date | | quantity | int | | price | decimal | -…...

管理学院权限管理系统开发总结
文章目录 🎓 管理学院权限管理系统开发总结 - 现代化Web应用实践之路📝 项目概述🏗️ 技术架构设计后端技术栈前端技术栈 💡 核心功能特性1. 用户管理模块2. 权限管理系统3. 统计报表功能4. 用户体验优化 🗄️ 数据库设…...

在QWebEngineView上实现鼠标、触摸等事件捕获的解决方案
这个问题我看其他博主也写了,要么要会员、要么写的乱七八糟。这里我整理一下,把问题说清楚并且给出代码,拿去用就行,照着葫芦画瓢。 问题 在继承QWebEngineView后,重写mousePressEvent或event函数无法捕获鼠标按下事…...

Windows安装Miniconda
一、下载 https://www.anaconda.com/download/success 二、安装 三、配置镜像源 Anaconda/Miniconda pip 配置清华镜像源_anaconda配置清华源-CSDN博客 四、常用操作命令 Anaconda/Miniconda 基本操作命令_miniconda创建环境命令-CSDN博客...

【Linux系统】Linux环境变量:系统配置的隐形指挥官
。# Linux系列 文章目录 前言一、环境变量的概念二、常见的环境变量三、环境变量特点及其相关指令3.1 环境变量的全局性3.2、环境变量的生命周期 四、环境变量的组织方式五、C语言对环境变量的操作5.1 设置环境变量:setenv5.2 删除环境变量:unsetenv5.3 遍历所有环境…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...
