【C++代码】背包问题,完全背包,多重背包,打家劫舍,动态规划--代码随想录
爬楼梯(plus)
-
一步一个台阶,两个台阶,三个台阶,…,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢?
-
1阶,2阶,… m阶就是物品,楼顶就是背包。每一阶可以重复使用,例如跳了1阶,还可以继续跳1阶。问跳到楼顶有几种方法其实就是问装满背包有几种方法。此时大家应该发现这就是一个完全背包问题了!
-
确定dp数组以及下标的含义:dp[i]:爬到有i个台阶的楼顶,有dp[i]种方法。
-
确定递推公式:那么递推公式为:dp[i] += dp[i - j]
-
dp数组如何初始化:既然递归公式是 dp[i] += dp[i - j],那么dp[0] 一定为1,dp[0]是递归中一切数值的基础所在,如果dp[0]是0的话,其他数值都是0了。
-
确定遍历顺序:这是背包里求排列问题,先背包,后物品。
-
Int clam(int m,int n){//n表示楼层高度,m表示步数选择1到mVector<int> dp(n+1,0);Dp[0]=1;For(int i=0;i<=n;i++){For(int j=1;i<=m;j++){If(i-j>=0){Dp[i]+=dp[i-j];}}}Return dp[n]; } -
时间复杂度: O(nm);空间复杂度: O(n)
题目:零钱兑换
-
给你一个整数数组
coins,表示不同面额的硬币;以及一个整数amount,表示总金额。计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回-1。你可以认为每种硬币的数量是无限的。 -
题目中说每种硬币的数量是无限的,可以看出是典型的完全背包问题。
- 确定dp数组以及下标的含义:dp[j]:凑足总额为j所需钱币的最少个数为dp[j]
- 确定递推公式:凑足总额为j - coins[i]的最少个数为dp[j - coins[i]],那么只需要加上一个钱币coins[i]即dp[j - coins[i]] + 1就是dp[j](考虑coins[i]);所以dp[j] 要取所有 dp[j - coins[i]] + 1 中最小的。递推公式:dp[j] = min(dp[j - coins[i]] + 1, dp[j]);
- dp数组如何初始化:首先凑足总金额为0所需钱币的个数一定是0,那么dp[0] = 0;考虑到递推公式的特性,dp[j]必须初始化为一个最大的数,否则就会在min(dp[j - coins[i]] + 1, dp[j])比较的过程中被初始值覆盖。
- 确定遍历顺序:本题求钱币最小个数,那么钱币有顺序和没有顺序都可以,都不影响钱币的最小个数。所以先背包或先物品对结果没影响。
-
class Solution { public:int coinChange(vector<int>& coins, int amount) {vector<int> dp(amount+1,INT_MAX);dp[0]=0;for(int i=0;i<=amount;i++){for(int j=0;j<coins.size();j++){if(i-coins[j]>=0 && dp[i-coins[j]]!=INT_MAX){dp[i] = min(dp[i],dp[i-coins[j]]+1);}}}return dp[amount]==INT_MAX?-1:dp[amount];} }; -
时间复杂度: O(n * amount),其中 n 为 coins 的长度;空间复杂度: O(amount)
题目:完全平方数
-
给你一个整数
n,返回 和为n的完全平方数的最少数量 。完全平方数 是一个整数,其值等于另一个整数的平方;换句话说,其值等于一个整数自乘的积。例如,1、4、9和16都是完全平方数,而3和11不是。 -
确定dp数组(dp table)以及下标的含义:dp[j]:和为j的完全平方数的最少数量为dp[j]
-
确定递推公式:dp[j] 可以由dp[j - i * i]推出, dp[j - i * i] + 1 便可以凑成dp[j]。此时我们要选择最小的dp[j],所以递推公式:dp[j] = min(dp[j - i * i] + 1, dp[j]);
-
dp数组如何初始化:dp[0]表示 和为0的完全平方数的最小数量,那么dp[0]一定是0。从递归公式dp[j] = min(dp[j - i * i] + 1, dp[j]);中可以看出每次dp[j]都要选最小的,所以非0下标的dp[j]一定要初始为最大值,这样dp[j]在递推的时候才不会被初始值覆盖。
-
class Solution { public:int numSquares(int n) {vector<int> dp(n+1,INT_MAX);dp[0]=0;for(int i=0;i<=n;i++){for(int j=1;j*j<=i;j++){dp[i] = min(dp[i],dp[i-j*j]+1);}}return dp[n];} };
题目:单词拆分
-
给你一个字符串
s和一个字符串列表wordDict作为字典。请你判断是否可以利用字典中出现的单词拼接出s。**注意:**不要求字典中出现的单词全部都使用,并且字典中的单词可以重复使用。 -
单词就是物品,字符串s就是背包,单词能否组成字符串s,就是问物品能不能把背包装满。拆分时可以重复使用字典中的单词,说明就是一个完全背包!
- 确定dp数组以及下标的含义:dp[i] : 字符串长度为i的话,dp[i]为true,表示可以拆分为一个或多个在字典中出现的单词。
- 确定递推公式:如果确定dp[j] 是true,且 [j, i] 这个区间的子串出现在字典里,那么dp[i]一定是true。(j < i )。所以递推公式是 if([j, i] 这个区间的子串出现在字典里 && dp[j]是true) 那么 dp[i] = true。
- dp数组如何初始化:从递推公式中可以看出,dp[i] 的状态依靠 dp[j]是否为true,那么dp[0]就是递推的根基,dp[0]一定要为true,否则递推下去后面都都是false了。
- 确定遍历顺序:本题其实我们求的是排列数,为什么呢。 拿 s = “applepenapple”, wordDict = [“apple”, “pen”] 举例。“apple”, “pen” 是物品,那么我们要求 物品的组合一定是 “apple” + “pen” + “apple” 才能组成 “applepenapple”。所以说,本题一定是 先遍历 背包,再遍历物品。
-
class Solution { public:bool wordBreak(string s, vector<string>& wordDict) {unordered_set<string> wordset(wordDict.begin(),wordDict.end());vector<bool> dp(s.size()+1,false);dp[0]=true;for(int i=1;i<=s.size();i++){for(int j=0;j<i;j++){string word=s.substr(j,i-j);//substr(起始位置,截取的个数)if(wordset.find(word)!=wordset.end() && dp[j]){dp[i]=true;}} }return dp[s.size()];} }; -
时间复杂度:O(n^3),因为substr返回子串的副本是O(n)的复杂度(这里的n是substring的长度);空间复杂度:O(n)
多重背包
- 有N种物品和一个容量为V 的背包。第i种物品最多有Mi件可用,每件耗费的空间是Ci ,价值是Wi 。求解将哪些物品装入背包可使这些物品的耗费的空间 总和不超过背包容量,且价值总和最大。每件物品最多有Mi件可用,把Mi件摊开,其实就是一个01背包问题了。
题目:打家劫舍
-
你是一个专业的小偷,计划偷窃沿街的房屋。每间房内都藏有一定的现金,影响你偷窃的唯一制约因素就是相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警。给定一个代表每个房屋存放金额的非负整数数组,计算你 不触动警报装置的情况下 ,一夜之内能够偷窃到的最高金额。
-
当前房屋偷与不偷取决于 前一个房屋和前两个房屋是否被偷了。所以这里就更感觉到,当前状态和前面状态会有一种依赖关系,那么这种依赖关系都是动规的递推公式。当然以上是大概思路,打家劫舍是dp解决的经典问题,接下来我们来动规五部曲分析如下:
- 确定dp数组(dp table)以及下标的含义:如果偷第i房间,那么dp[i] = dp[i - 2] + nums[i] ,即:第i-1房一定是不考虑的,找出 下标i-2(包括i-2)以内的房屋,最多可以偷窃的金额为dp[i-2] 加上第i房间偷到的钱。如果不偷第i房间,那么dp[i] = dp[i - 1],即考 虑i-1房,(注意这里是考虑,并不是一定要偷i-1房,这是很多同学容易混淆的点)。然后dp[i]取最大值,即dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);
- dp数组如何初始化:从递推公式dp[i] = max(dp[i - 2] + nums[i], dp[i - 1]);可以看出,递推公式的基础就是dp[0] 和 dp[1];从dp[i]的定义上来讲,dp[0] 一定是 nums[0],dp[1]就是nums[0]和nums[1]的最大值即:dp[1] = max(nums[0], nums[1]);
-
class Solution { public:int rob(vector<int>& nums) {if(nums.size()==0){return 0;}if(nums.size()==1){return nums[0];}vector<int> dp(nums.size());dp[0]=nums[0];dp[1]=max(nums[0],nums[1]);for(int i=2;i<nums.size();i++){dp[i]=max(dp[i-2]+nums[i],dp[i-1]);}return dp[nums.size()-1];} }; -
时间复杂度: O(n);空间复杂度: O(n)
题目:打家劫舍 II
-
你是一个专业的小偷,计划偷窃沿街的房屋,每间房内都藏有一定的现金。这个地方所有的房屋都 围成一圈 ,这意味着第一个房屋和最后一个房屋是紧挨着的。同时,相邻的房屋装有相互连通的防盗系统,如果两间相邻的房屋在同一晚上被小偷闯入,系统会自动报警 。给定一个代表每个房屋存放金额的非负整数数组,计算你 在不触动警报装置的情况下 ,今晚能够偷窃到的最高金额。
-
class Solution { public:int robpart(vector<int> &numspart,int start,int end){if(end==start) return numspart[start];vector<int> dp(numspart.size());dp[start] = numspart[start];dp[start+1] = max(numspart[start],numspart[start+1]);for(int i=start+2;i<=end;i++){dp[i] = max(dp[i-2]+numspart[i],dp[i-1]);// cout<<dp[i]<<" ";}return dp[end];}int rob(vector<int>& nums) {if(nums.size()==0){return 0;}if(nums.size()==1){return nums[0];}int left = robpart(nums,0,nums.size()-2);// cout<<endl;int right = robpart(nums,1,nums.size()-1);// cout<<left<<" "<<right<<endl;// return left>right?left:right;return max(left,right);} };
题目:打家劫舍 III
-
小偷又发现了一个新的可行窃的地区。这个地区只有一个入口,我们称之为
root。除了root之外,每栋房子有且只有一个“父“房子与之相连。一番侦察之后,聪明的小偷意识到“这个地方的所有房屋的排列类似于一棵二叉树”。 如果 两个直接相连的房子在同一天晚上被打劫 ,房屋将自动报警。给定二叉树的root。返回 在不触动警报的情况下 ,小偷能够盗取的最高金额 。 -
这道题目算是树形dp的入门题目,因为是在树上进行状态转移,在讲解二叉树的时候说过递归三部曲,那么下面我以递归三部曲为框架,其中融合动规五部曲的内容来进行讲解。
- 确定递归函数的参数和返回值:要求一个节点 偷与不偷的两个状态所得到的金钱,那么返回值就是一个长度为2的数组。所以dp数组(dp table)以及下标的含义:下标为0记录不偷该节点所得到的的最大金钱,下标为1记录偷该节点所得到的的最大金钱。
- 确定终止条件:在遍历的过程中,如果遇到空节点的话,很明显,无论偷还是不偷都是0,所以就返回
- 确定遍历顺序:首先明确的是使用后序遍历。 因为要通过递归函数的返回值来做下一步计算。通过递归左节点,得到左节点偷与不偷的金钱。通过递归右节点,得到右节点偷与不偷的金钱。
- 确定单层递归的逻辑:如果是偷当前节点,那么左右孩子就不能偷,val1 = cur->val + left[0] + right[0]; 如果不偷当前节点,那么左右孩子就可以偷,至于到底偷不偷一定是选一个最大的,所以:val2 = max(left[0], left[1]) + max(right[0], right[1]);最后当前节点的状态就是{val2, val1}; 即:{不偷当前节点得到的最大金钱,偷当前节点得到的最大金钱}
-
/*** Definition for a binary tree node.* struct TreeNode {* int val;* TreeNode *left;* TreeNode *right;* TreeNode() : val(0), left(nullptr), right(nullptr) {}* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}* };*/ class Solution { public:vector<int> robtree(TreeNode *cur){if(cur==nullptr){return vector<int>{0,0};}vector<int> left=robtree(cur->left);vector<int> right=robtree(cur->right);int val1=cur->val+left[0]+right[0];int val2=max(left[0],left[1])+max(right[0],right[1]);return {val2,val1};}int rob(TreeNode* root) {vector<int> res=robtree(root);return max(res[0],res[1]);} }; -
时间复杂度:O(n),每个节点只遍历了一次;空间复杂度:O(log n),算上递推系统栈的空间
相关文章:

【C++代码】背包问题,完全背包,多重背包,打家劫舍,动态规划--代码随想录
爬楼梯(plus) 一步一个台阶,两个台阶,三个台阶,…,直到 m个台阶。问有多少种不同的方法可以爬到楼顶呢? 1阶,2阶,… m阶就是物品,楼顶就是背包。每一阶可以重复使用,例如…...

阿里云创始人王坚:云计算和GPT的关系,就是电和电机的关系
10月31日,在2023云栖大会,中国工程院院士、阿里云创始人王坚以《云计算的第三次浪潮》为主题发表演讲,他认为人工智能和云计算的结合,带来云计算的第三次浪潮,它不会在一年、两年完成,它可能会给我们十年、…...

python爬取豆瓣电影Top250数据
本次爬虫案例使用Python语言编写,使用了requests库进行网页请求,使用了BeautifulSoup库进行网页解析,使用了openpyxl库进行数据的保存。 案例中的爬虫目标是豆瓣电影Top250,通过循环访问不同页面进行数据的爬取。在每个页面上&am…...
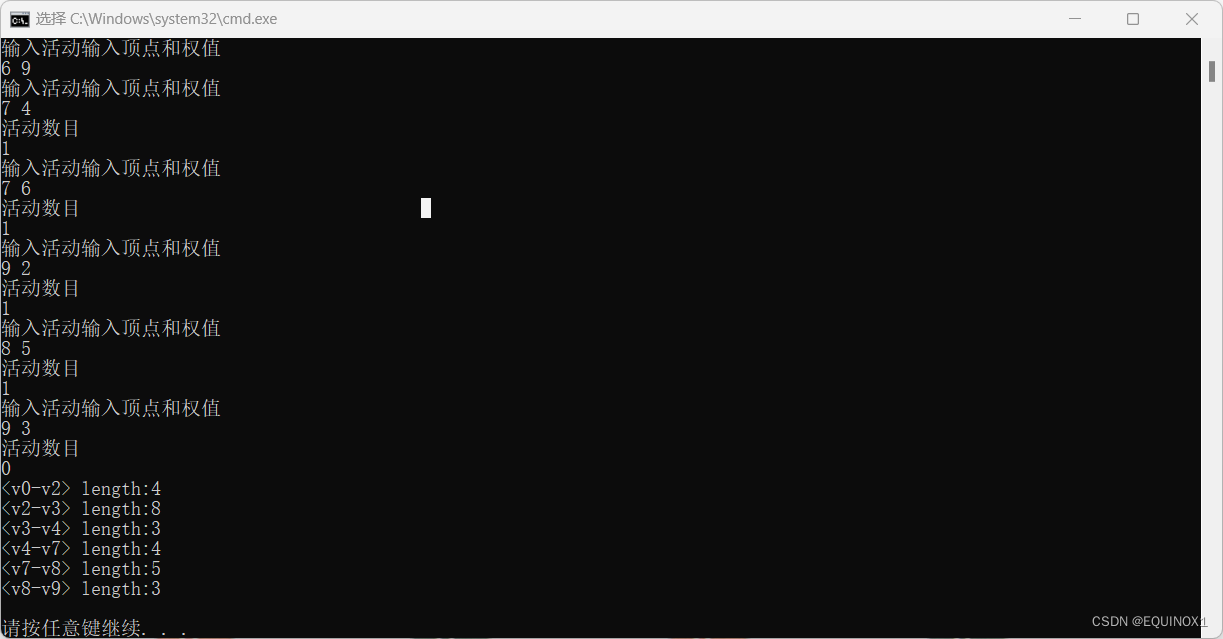
关键路径及关键路径算法[C/C++]
文章目录 关键路径引例AOE网关键路径与关键活动关键路径算法引例与原理关键路径算法的实现边的存储结构代码实现运行示例 关键路径 关于拓扑排序的内容见拓扑排序详解 引例 通过拓扑排序我们可以解决一个工程是否可以顺序进行的问题,拓扑排序把一个工程分成了若干…...

nginx http 跳转到https
改 Nginx 配置文件 在您安装了 SSL 证书之后,您需要修改 Nginx 的配置文件以启用 HTTPS 和 HTTP 自动跳转 HTTPS。 打开 Nginx 配置文件(通常位于 /etc/nginx/nginx.conf),找到您的网站配置块。在该配置块中添加以下内容&#x…...

可靠的互联网兼职平台,平常可以做副业充实生活
在互联网时代,越来越多的人开始通过网络来寻找兼职副业的机会,能够更灵活地安排自己的时间,实现自己的收入增值。那么找到一个正规可靠的线上兼职平台就是一个比较重要的事情,这里分享几个正规靠谱的线上兼职副业平台,…...
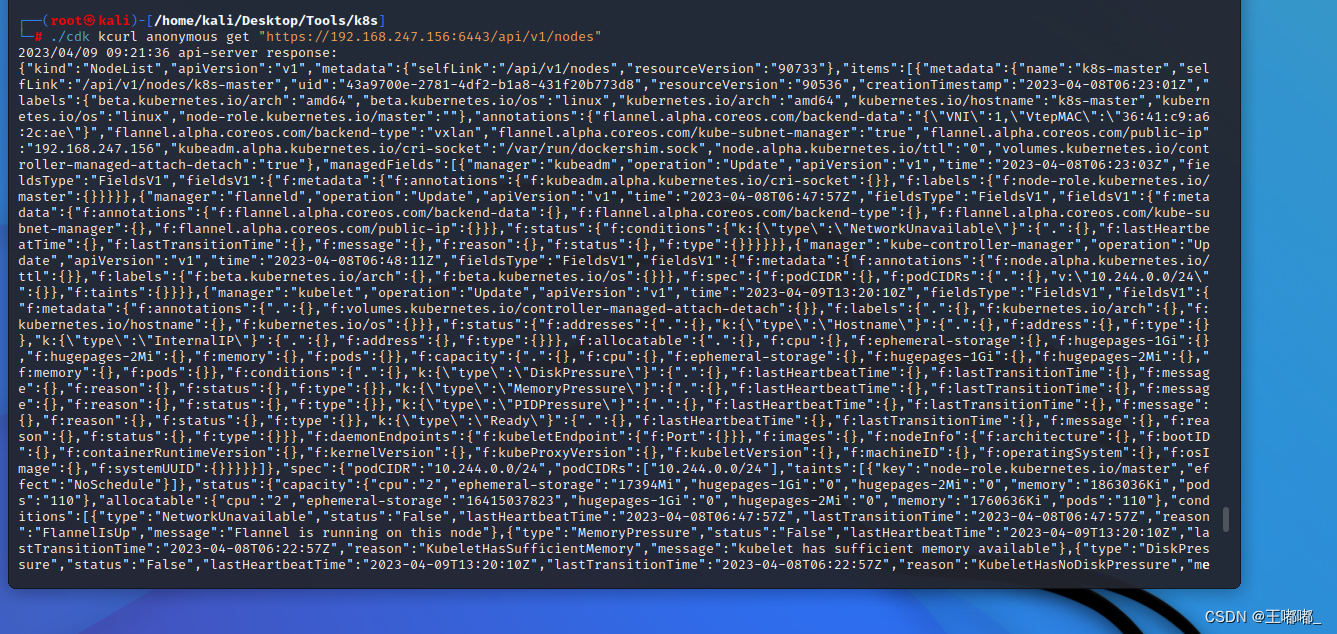
云安全—K8s APi Server 6443 攻击面
0x00 前言 在未授权的一文中,详细描述了k8s api中的8080端口未授权的问题,那么本篇主要来说6443端口的利用。 0x01 API连接攻击面 1.匿名用户访问 匿名开放方式:kubectl create clusterrolebinding cluster-system-anonymous --clusterro…...

【案例实战】NodeJS+Vue3+MySQL实现列表查询功能
这篇文章,给大家带来一个列表查询的功能,从前端到后端的一个综合案例实战。 采用vue3作为前端开发,nodejs作为后端开发。 首先我们先来看一下完成的页面效果。点击分页,可以切换到上一页、下一页。搜索框可以进行模糊查询。 后端…...
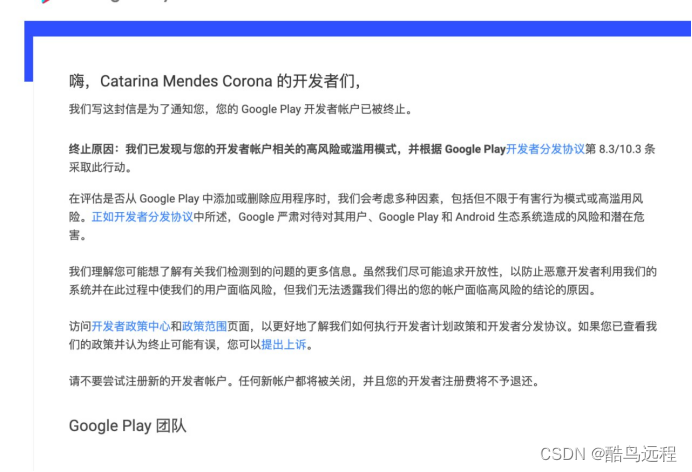
Google play开发者账号被封的几种常见原因及相关解决思路
在Google paly上,每天都有大量的应用被成功发布,同时也有很多开发者账号被封禁。特别是在今年的十月份之前,谷歌的"封号潮"给很多开发者带来了沉重的打击。不过,令人欣慰的是,自十月份之后,情况逐…...

深入理解计算机系统CS213学习笔记
Lecture 01 1. 计算机表示数字 int 整数运算可能会出现错误,超过32位时会出现溢出。 float 浮点数不适用结合律,因为浮点数表示的精度有限。 根其原因,是用有限的位数表示无限的数字空间。 2.利用分层的存储系统,使程序运行更…...
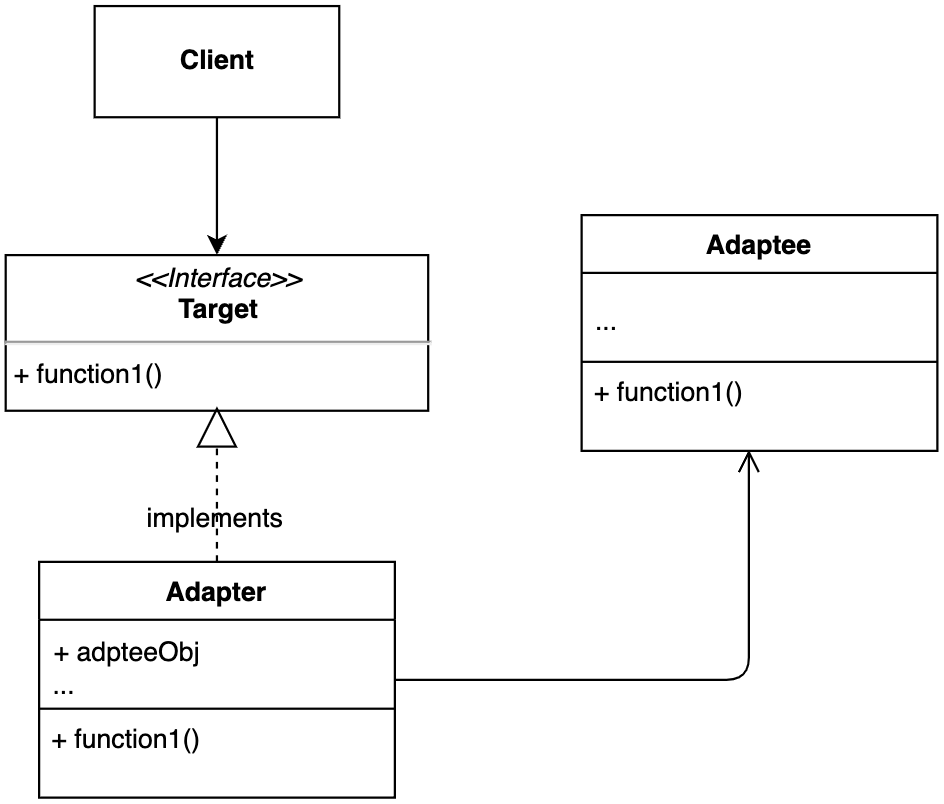
【设计模式】第8节:结构型模式之“适配器模式”
一、简介 适配器模式是用来做适配的,它将不兼容的接口转换为可兼容的接口,让原本由于接口不兼容而不能一起工作的类可以一起工作。 适配器模式角色: 请求者client:调用服务的角色目标Target:定义了Client要使用的功…...
Stable Diffusion WebUI扩展openpose-editor如何使用
先上地址: GitHub - fkunn1326/openpose-editor: Openpose Editor for AUTOMATIC1111s stable-diffusion-webuiOpenpose Editor for AUTOMATIC1111s stable-diffusion-webui - GitHub - fkunn1326/openpose-editor: Openpose Editor for AUTOMATIC1111s stable-diffusion-webu…...

企业网络带宽使用情况检查技巧
想要提高网络性能的企业通常会考虑限制对占用带宽的应用程序(如社交媒体和视频流应用程序)的访问,但对于那些真正需要获得高效网络的人来说,这还不够,您需要定期跟踪带宽使用情况。 虽然有许多工具可以帮助您检查网络…...
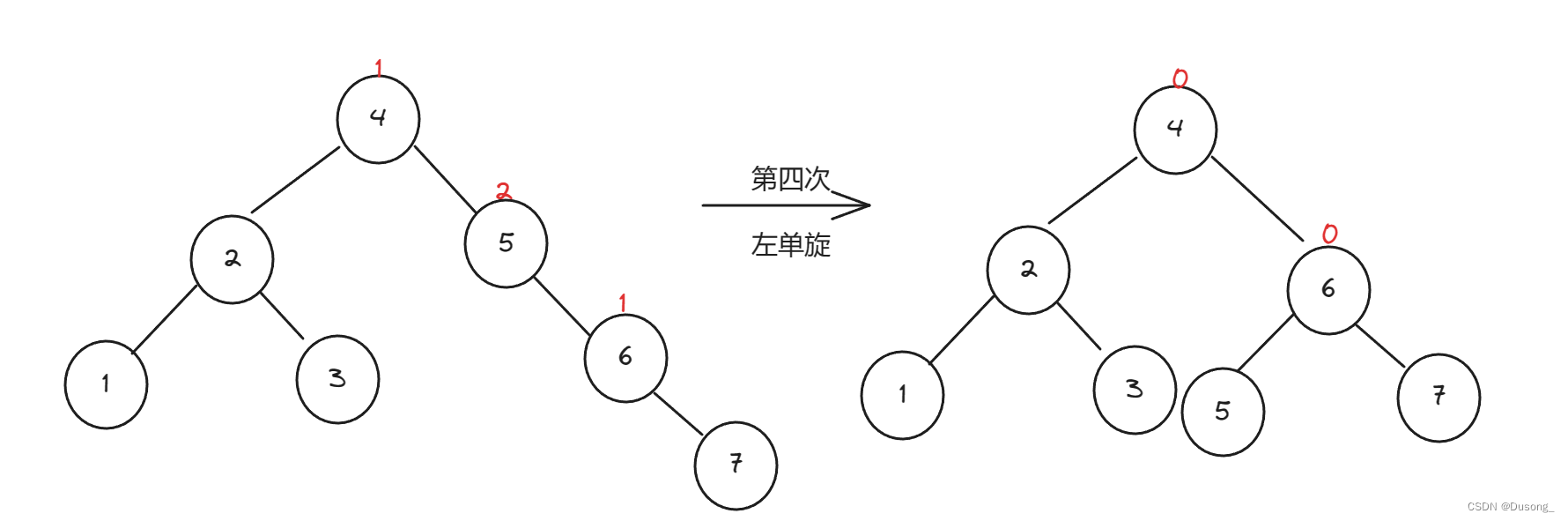
C/C++笔试易错与高频题型图解知识点(三)——数据结构部分(持续更新中)
目录 1. 排序 1.1 冒泡排序的改进 2. 二叉树 2.1 二叉树的性质 3. 栈 & 队列 3.1 循环队列 3.2 链式队列 4. 平衡二叉搜索树——AVL树、红黑树 5 优先级队列(堆) 1. 排序 1.1 冒泡排序的改进 下面的排序方法中,关键字比较次数与记录的初…...
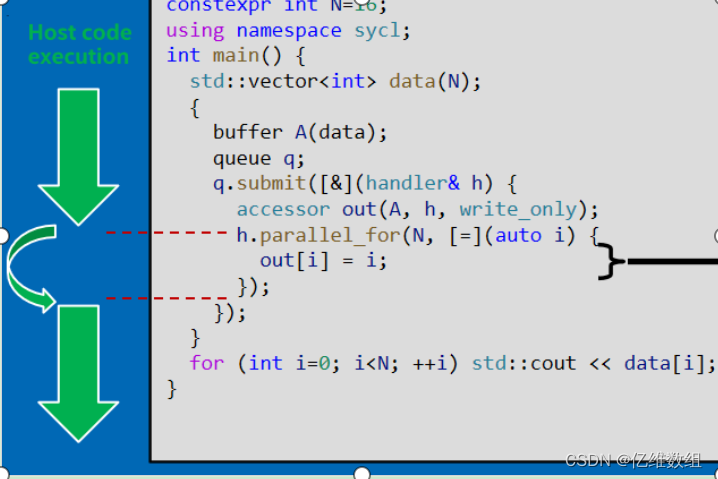
Intel oneAPI笔记--oneAPI简介、SYCL编程简介
oneAPI简介 Intel oneAPI是Intel提供的统一编程模型和软件开发框架。 它旨在简化可充分利用英特尔各种硬件架构(包括 CPU、GPU 和 FPGA)的应用程序的开发 oneAPI一个重要的特性是开放性,支持多种类型的架构和不同的硬件供应商,是…...
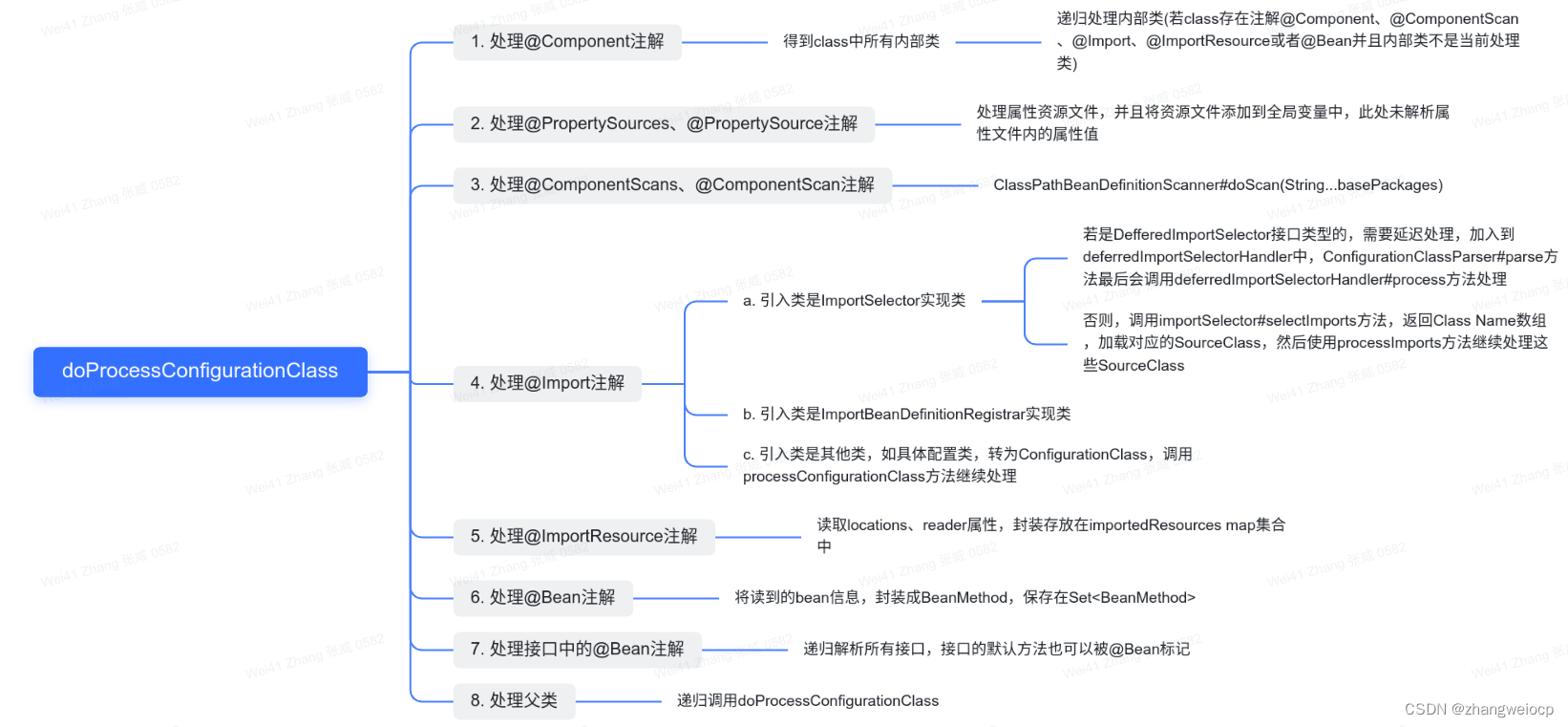
Spring IOC - ConfigurationClassPostProcessor源码解析
上文提到Spring在Bean扫描过程中,会手动将5个Processor类注册到beanDefinitionMap中,其中ConfigurationClassPostProcessor就是本文将要讲解的内容,该类会在refresh()方法中通过调用invokeBeanFactoryPosstProcessors(beanFactory)被调用。 5…...
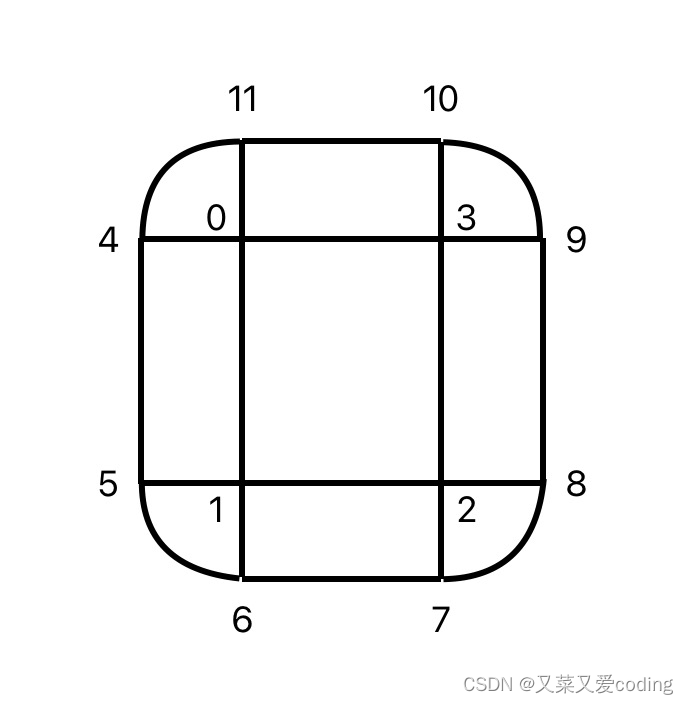
Android OpenGL ES 2.0入门实践
本文既然是入门实践,就先从简单的2D图形开始,首先,参考两篇官方文档搭建个框架,便于写OpenGL ES相关的代码:构建 OpenGL ES 环境、OpenGL ES 2.0 及更高版本中的投影和相机视图。 先上代码,代码效果如下图…...

sql语句性能进阶必须了解的知识点——索引失效分析
在前面的文章中讲解了sql语句的优化策略 sql语句性能进阶必须了解的知识点——sql语句的优化方案-CSDN博客 sql语句的优化重点还有一处,那就是—— 索引!好多sql语句慢的本质原因就是设置的索引失效或者根本没有建立索引!今天我们就来总结一…...
ctfhub技能树web题目全解
Rce 文件包含 靶场环境 重点是这个代码,strpos,格式是这样的strpoc(1,2,3) 1是要搜索的字符串,必须有;2是要查询的字符串,必须有;3是在何处开始查询&#…...

AMD、CMD、UMD是什么?
AMD(Asynchronous Module Definition)、CMD(Common Module Definition)和UMD(Universal Module Definition)是JavaScript模块化规范,用于管理和组织JavaScript代码的模块化加载和依赖管理。 1:AMD(异步模块定义): AMD是由RequireJS提出的模块化规范。它支持异步加载…...

【Java学习笔记】Arrays类
Arrays 类 1. 导入包:import java.util.Arrays 2. 常用方法一览表 方法描述Arrays.toString()返回数组的字符串形式Arrays.sort()排序(自然排序和定制排序)Arrays.binarySearch()通过二分搜索法进行查找(前提:数组是…...
)
是否存在路径(FIFOBB算法)
题目描述 一个具有 n 个顶点e条边的无向图,该图顶点的编号依次为0到n-1且不存在顶点与自身相连的边。请使用FIFOBB算法编写程序,确定是否存在从顶点 source到顶点 destination的路径。 输入 第一行两个整数,分别表示n 和 e 的值(1…...

dify打造数据可视化图表
一、概述 在日常工作和学习中,我们经常需要和数据打交道。无论是分析报告、项目展示,还是简单的数据洞察,一个清晰直观的图表,往往能胜过千言万语。 一款能让数据可视化变得超级简单的 MCP Server,由蚂蚁集团 AntV 团队…...

Springboot社区养老保险系统小程序
一、前言 随着我国经济迅速发展,人们对手机的需求越来越大,各种手机软件也都在被广泛应用,但是对于手机进行数据信息管理,对于手机的各种软件也是备受用户的喜爱,社区养老保险系统小程序被用户普遍使用,为方…...

rnn判断string中第一次出现a的下标
# coding:utf8 import torch import torch.nn as nn import numpy as np import random import json""" 基于pytorch的网络编写 实现一个RNN网络完成多分类任务 判断字符 a 第一次出现在字符串中的位置 """class TorchModel(nn.Module):def __in…...

Python 包管理器 uv 介绍
Python 包管理器 uv 全面介绍 uv 是由 Astral(热门工具 Ruff 的开发者)推出的下一代高性能 Python 包管理器和构建工具,用 Rust 编写。它旨在解决传统工具(如 pip、virtualenv、pip-tools)的性能瓶颈,同时…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

FFmpeg:Windows系统小白安装及其使用
一、安装 1.访问官网 Download FFmpeg 2.点击版本目录 3.选择版本点击安装 注意这里选择的是【release buids】,注意左上角标题 例如我安装在目录 F:\FFmpeg 4.解压 5.添加环境变量 把你解压后的bin目录(即exe所在文件夹)加入系统变量…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

tomcat入门
1 tomcat 是什么 apache开发的web服务器可以为java web程序提供运行环境tomcat是一款高效,稳定,易于使用的web服务器tomcathttp服务器Servlet服务器 2 tomcat 目录介绍 -bin #存放tomcat的脚本 -conf #存放tomcat的配置文件 ---catalina.policy #to…...
