DAY42 1049.最后一块石头的重量II + 494.目标和 + 474.一和零
1049.最后一块石头的重量II
题目要求:有一堆石头,每块石头的重量都是正整数。
每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x <= y。那么粉碎的可能结果如下:
如果 x == y,那么两块石头都会被完全粉碎;
如果 x != y,那么重量为 x 的石头将会完全粉碎,而重量为 y 的石头新重量为 y-x。
最后,最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下,就返回 0。
思路
目标是尽量让石头分成重量相同的两堆,相撞之后剩下的石头最小,这样就转化成01背包问题了。
dp[j]表示容量为j的背包,可以装载的最大重量为dp[j]
遍历顺序:如果使用一维dp数组,物品遍历的for循环放在外层,遍历背包的for循环房子啊内层,且内层for循环倒序遍历。
分成两堆石头,一堆石头的总重量是dp[target],另一堆就是sum-dp[target]
在计算target时候,target=sum/2是向下取整。所以sum-dp[target]一定大于等于dp[target]。那么相撞后剩下的最小石头重量就是(sum-dp[target])-dp[target]
class Solution {
public:int lastStoneWeightII(vector<int>& stones) {vector<int> dp(15001, 0);int sum = 0;for (int i = 0; i < stones.size(); ++i) {sum += stones[i];}int target = sum / 2;for (int i = 0; i < stones.size(); ++i) {for (int j = target; j >= stones[i]; --j) {dp[j] = max(dp[j], dp[j-stones[i]] + stones[i]);}}return sum - dp[target] - dp[target];}
};- 时间复杂度:O(m × n) , m是石头总重量(准确的说是总重量的一半),n为石头块数
- 空间复杂度:O(m)
494.目标和
题目要求:给定一个非负整数数组,a1, a2, ..., an, 和一个目标数,S。现在你有两个符号 + 和 -。对于数组中的任意一个整数,你都可以从 + 或 -中选择一个符号添加在前面。
返回可以使最终数组和为目标数 S 的所有添加符号的方法数。
思路
目前我们已经有了目标target=s,假设加法的总和为x,那么减法对应的总和就是sum-x。所以我们要求的是x-(sum-x)=target,x=(target+sum)/2。此时问题就转化为,装满容量为x的背包有几种方法。
x的计算是向下取整的,所以如果target+sum为奇数,那么本提无解。如果S的绝对值大于sum也是无解的。
装满背包有几种方法,其实就是一个组合问题了。
递推公式:只要有nums[i],凑成dp[j]就有dp[j - nums[i]] 种方法。
那么凑整dp[5]有多少方法呢,也就是把 所有的 dp[j - nums[i]] 累加起来。
dp数组的初始化:
从递推公式可以看出,在初始化的时候dp[0] 一定要初始化为1,因为dp[0]是在公式中一切递推结果的起源,如果dp[0]是0的话,递推结果将都是0。
这里有录友可能认为从dp数组定义来说 dp[0] 应该是0,也有录友认为dp[0]应该是1。
其实不要硬去解释它的含义,咱就把 dp[0]的情况带入本题看看应该等于多少。
如果数组[0] ,target = 0,那么 bagSize = (target + sum) / 2 = 0。 dp[0]也应该是1, 也就是说给数组里的元素 0 前面无论放加法还是减法,都是 1 种方法。
所以本题我们应该初始化 dp[0] 为 1。
可能有同学想了,那 如果是 数组[0,0,0,0,0] target = 0 呢。
其实 此时最终的dp[0] = 32,也就是这五个零 子集的所有组合情况,但此dp[0]非彼dp[0],dp[0]能算出32,其基础是因为dp[0] = 1 累加起来的。
dp[j]其他下标对应的数值也应该初始化为0,从递推公式也可以看出,dp[j]要保证是0的初始值,才能正确的由dp[j - nums[i]]推导出来。
确定遍历顺序:
我们讲过对于01背包问题一维dp的遍历,nums放在外循环,target在内循环,且内循环倒序。
class Solution {
public:int findTargetSumWays(vector<int>& nums, int target) {int sum = 0;for (int i = 0; i < nums.size(); ++i) sum += nums[i];if (abs(target) > sum) return 0;if ((target + sum) % 2 == 1) return 0;int bagSize = (target + sum) / 2;vector<int> dp(bagSize + 1, 0);dp[0] = 1;for (int i = 0; i < nums.size(); ++i) {for (int j = bagSize; j >= nums[i]; --j) {dp[j] += dp[j-nums[i]];}}return dp[bagSize];}
};474.一和零
题目要求:给你一个二进制字符串数组 strs 和两个整数 m 和 n 。
请你找出并返回 strs 的最大子集的大小,该子集中 最多 有 m 个 0 和 n 个 1 。
如果 x 的所有元素也是 y 的元素,集合 x 是集合 y 的 子集 。
示例 1:
-
输入:strs = ["10", "0001", "111001", "1", "0"], m = 5, n = 3
-
输出:4
-
解释:最多有 5 个 0 和 3 个 1 的最大子集是 {"10","0001","1","0"} ,因此答案是 4 。 其他满足题意但较小的子集包括 {"0001","1"} 和 {"10","1","0"} 。{"111001"} 不满足题意,因为它含 4 个 1 ,大于 n 的值 3 。
思路
本题中strs 数组里的元素就是物品,每个物品都是一个!
而m 和 n相当于是一个背包,两个维度的背包。
只不过这个背包有两个维度,一个是m 一个是n,而不同长度的字符串就是不同大小的待装物品。
- 确定dp数组(dp table)以及下标的含义
dp[i][j]:最多有i个0和j个1的strs的最大子集的大小为dp[i][j]。
- 确定递推公式
dp[i][j] 可以由前一个strs里的字符串推导出来,strs里的字符串有zeroNum个0,oneNum个1。
dp[i][j] 就可以是 dp[i - zeroNum][j - oneNum] + 1。
然后我们在遍历的过程中,取dp[i][j]的最大值。
所以递推公式:dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);
此时大家可以回想一下01背包的递推公式:dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
对比一下就会发现,字符串的zeroNum和oneNum相当于物品的重量(weight[i]),字符串本身的个数相当于物品的价值(value[i])。
这就是一个典型的01背包! 只不过物品的重量有了两个维度而已。
- dp数组如何初始化
因为物品价值不会是负数,初始为0,保证递推的时候dp[i][j]不会被初始值覆盖。
- 确定遍历顺序
01背包一定是外层for循环遍历物品,内层for循环遍历背包容量且从后向前遍历!
那么本题也是,物品就是strs里的字符串,背包容量就是题目描述中的m和n。
class Solution {
public:int findMaxForm(vector<string>& strs, int m, int n) {vector<vector<int>> dp(m+1, vector<int> (n+1, 0));for (string str : strs) {int oneNum = 0, zeroNum = 0;for (char c : str) {if (c == '0') zeroNum++;else oneNum++;}for (int i = m; i >= zeroNum; --i) {for (int j = n; j >= oneNum; --j) {dp[i][j] = max(dp[i][j], dp[i - zeroNum][j - oneNum] + 1);}}}return dp[m][n];}
};- 时间复杂度: O(kmn),k 为strs的长度
- 空间复杂度: O(mn)
相关文章:

DAY42 1049.最后一块石头的重量II + 494.目标和 + 474.一和零
1049.最后一块石头的重量II 题目要求:有一堆石头,每块石头的重量都是正整数。 每一回合,从中选出任意两块石头,然后将它们一起粉碎。假设石头的重量分别为 x 和 y,且 x < y。那么粉碎的可能结果如下: …...

uniapp原生插件之安卓华为统一扫码HMS Scan Kit
插件介绍 华为统一扫码服务(Scan Kit)提供便捷的条形码和二维码扫描、解析、生成能力 插件地址 安卓华为统一扫码HMS Scan Kit - DCloud 插件市场 超级福利 uniapp 插件购买超级福利 详细使用文档 详细使用文档 插件申请权限 android.permi…...
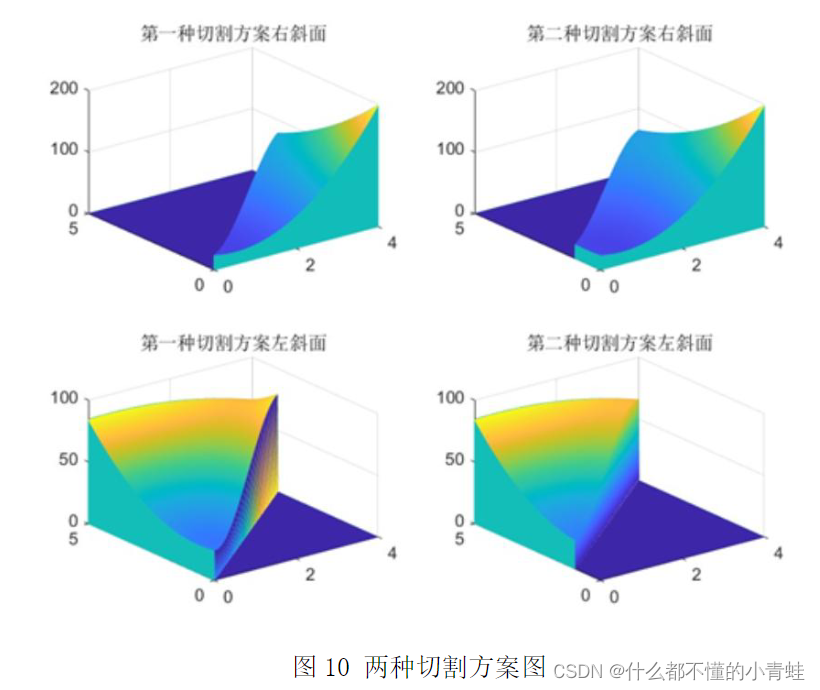
数模国赛——多波束测线问题模型建立研究分析
第一次参加数模国赛,太菜了~~~~意难平 问题一 画出与测线方向垂直的平面和海底坡面的交线构成一条与水平面夹角为𝐀的斜线的情况下的示意图进行分析,将覆盖宽度分为左覆盖宽度和右覆盖宽度,求出它们与海水深度和𝐀、…...
)
[AUTOSAR][诊断管理][ECU][$37] 请求退出传输。终止数据传输的(上传/下载)
文章目录 一、简介二、服务请求报文定义肯定响应支持的NRC三、示例流程Step 1:Step 2:报文示例:Step 1:请求RequestDownload(0x34)服务Step 2:请求TransferData (0x36)服务,传输数据Step 3:请求RequestTransferExit(0x37)服务总结:三、示例代码37_req_transfer_e…...

vue+canvas实现横跨整个页面的动态的波浪线(贝塞尔曲线)
本来写这个特效 我打算用css实现的,结果是一波三折,我太难了,最终没能用css实现,转战了canvas来实现。来吧先看效果图 当然这个图的波浪高度、频率、位置、速度都是可调的,请根据自己的需求调整,如果你讲波浪什么的调大一下 还有有摆动的效果哦。 以下是完整代码 <…...
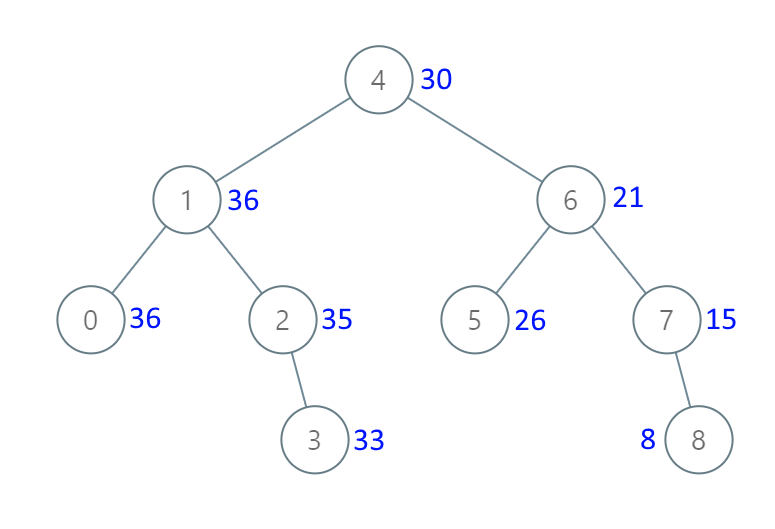
LeetCode算法题解| 669. 修剪二叉搜索树、108. 将有序数组转换为二叉搜索树、538. 把二叉搜索树转换为累加树
一、LeetCode 669. 修剪二叉搜索树 题目链接:669. 修剪二叉搜索树 题目描述: 给你二叉搜索树的根节点 root ,同时给定最小边界low 和最大边界 high。通过修剪二叉搜索树,使得所有节点的值在[low, high]中。修剪树 不应该 改变…...

直播界很火的无线领夹麦克风快充方案 Type-C接口 PD快充+无线麦克风可同时进行
当前市场上流行一款很火的直播神器,无线领夹麦克风(MIC),应用于网红直播,网课教学,采访录音,视频录制,视频会议等等场景。 麦克风对我们来说并不陌生,而且品类有很多。随…...
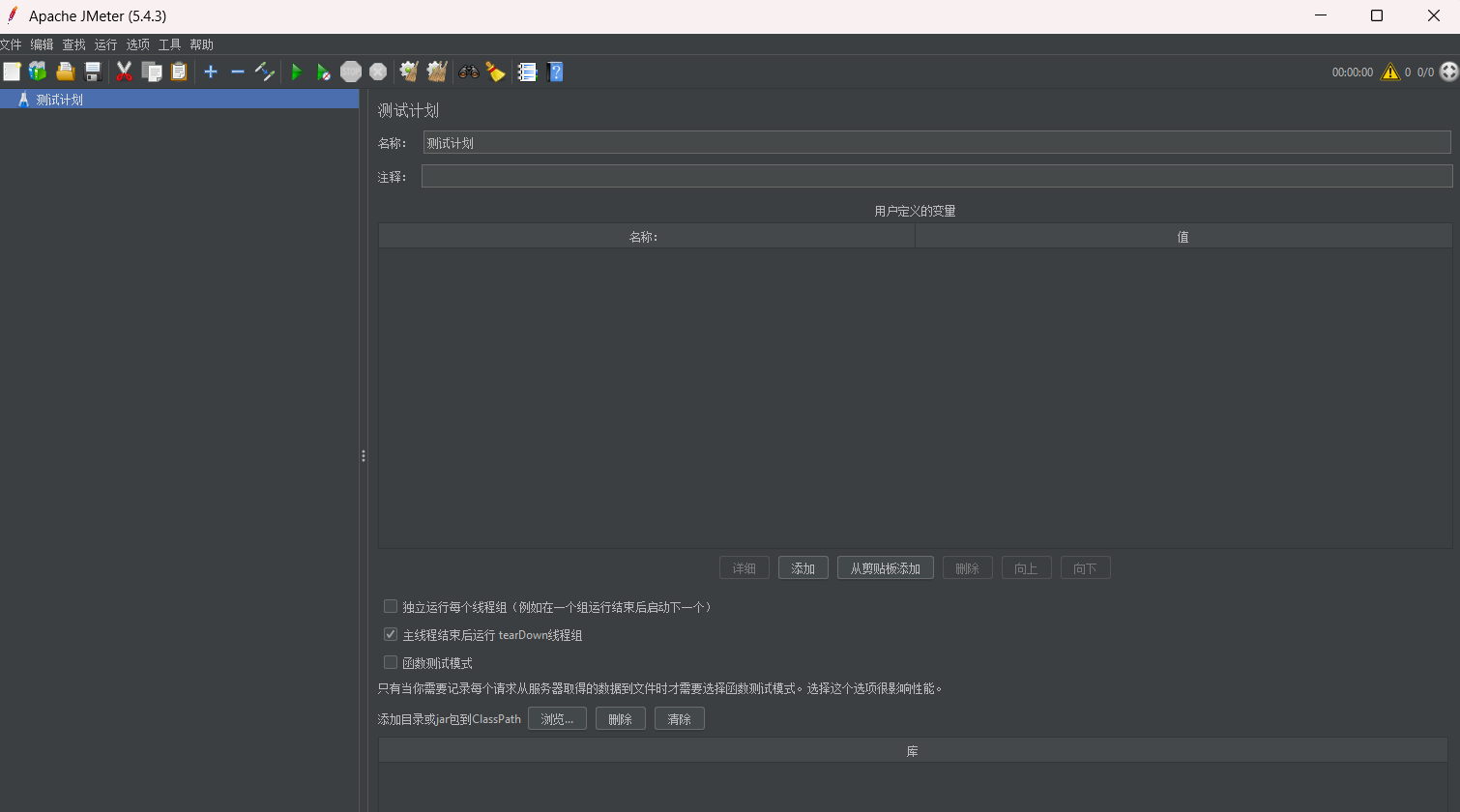
Jmeter 汉化中文语言
找到 bin -> jmeter.propertise 修改参数:languageen --> languagazh_CN OK!...
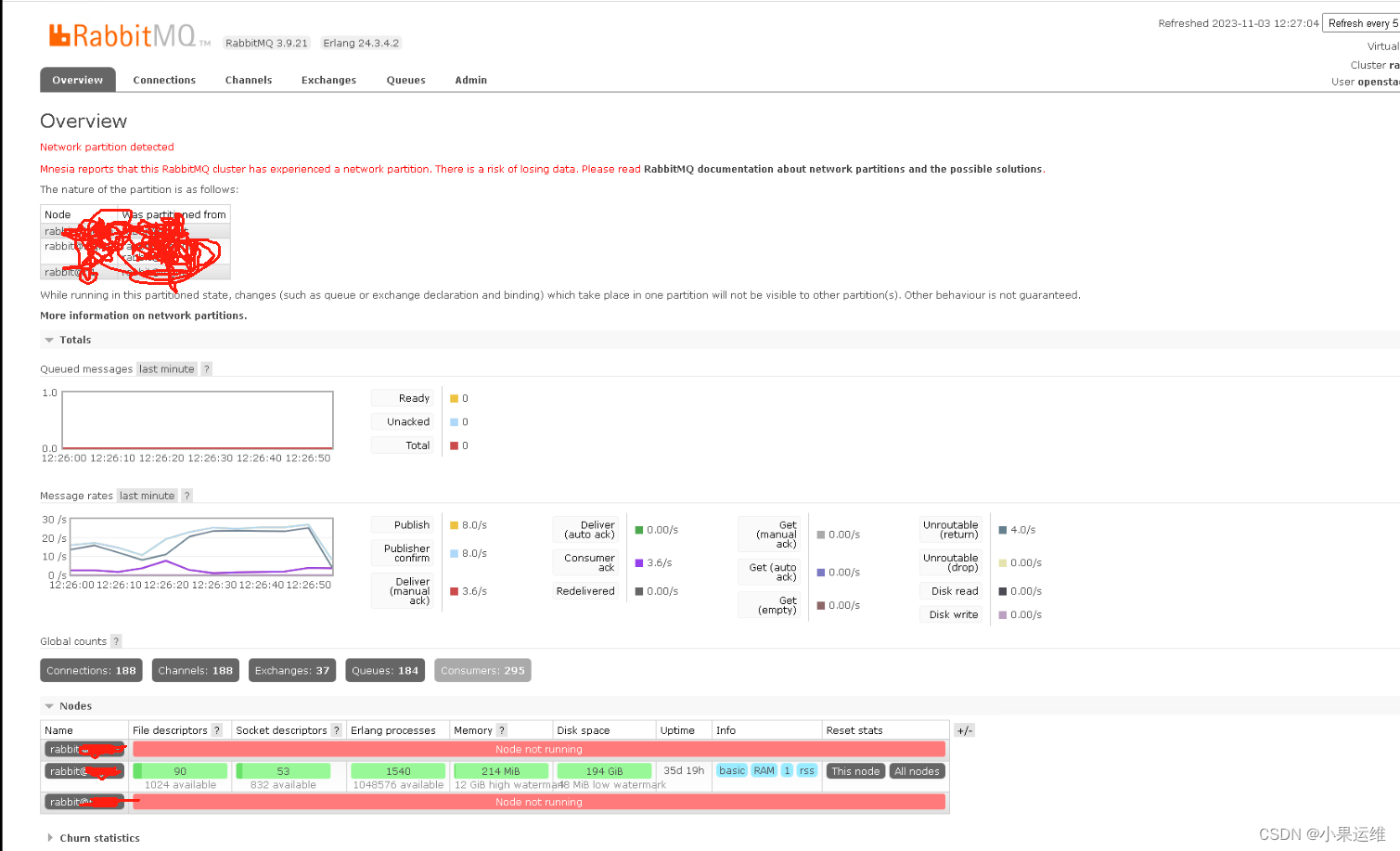
centos9 stream 下 rabbitmq高可用集群搭建及使用
RabbitMQ是一种常用的消息队列系统,可以快速搭建一个高可用的集群环境,以提高系统的弹性和可靠性。下面是搭建RabbitMQ集群的步骤: 基于centos9 stream系统 1. 安装Erlang和RabbitMQ 首先需要在所有节点上安装Erlang和RabbitMQ。建议使用官…...

代码随想录算法训练营第10天|232. 用栈实现队列 225. 用队列实现栈
JAVA代码编写 232. 用栈实现队列 请你仅使用两个栈实现先入先出队列。队列应当支持一般队列支持的所有操作(push、pop、peek、empty): 实现 MyQueue 类: void push(int x) 将元素 x 推到队列的末尾int pop() 从队列的开头移除…...

线上Kafka集群如何调整消息存储时间
这里是weihubeats,觉得文章不错可以关注公众号小奏技术,文章首发。拒绝营销号,拒绝标题党 Kafka版本 kafka_2.13-3.5.0 背景 Kafka 默认消息存储时间为7天,实际线上的业务使用Kafka更多的是一些数据统计之类的业务,大多是朝生夕…...
[迁移学习]DA-DETR基于信息融合的自适应检测模型
原文标题为:DA-DETR: Domain Adaptive Detection Transformer with Information Fusion;发表于CVPR2023 一、概述 本文所描述的模型基于DETR,DETR网络是一种基于Transformer的目标检测网络,详细原理可以参见往期文章:…...
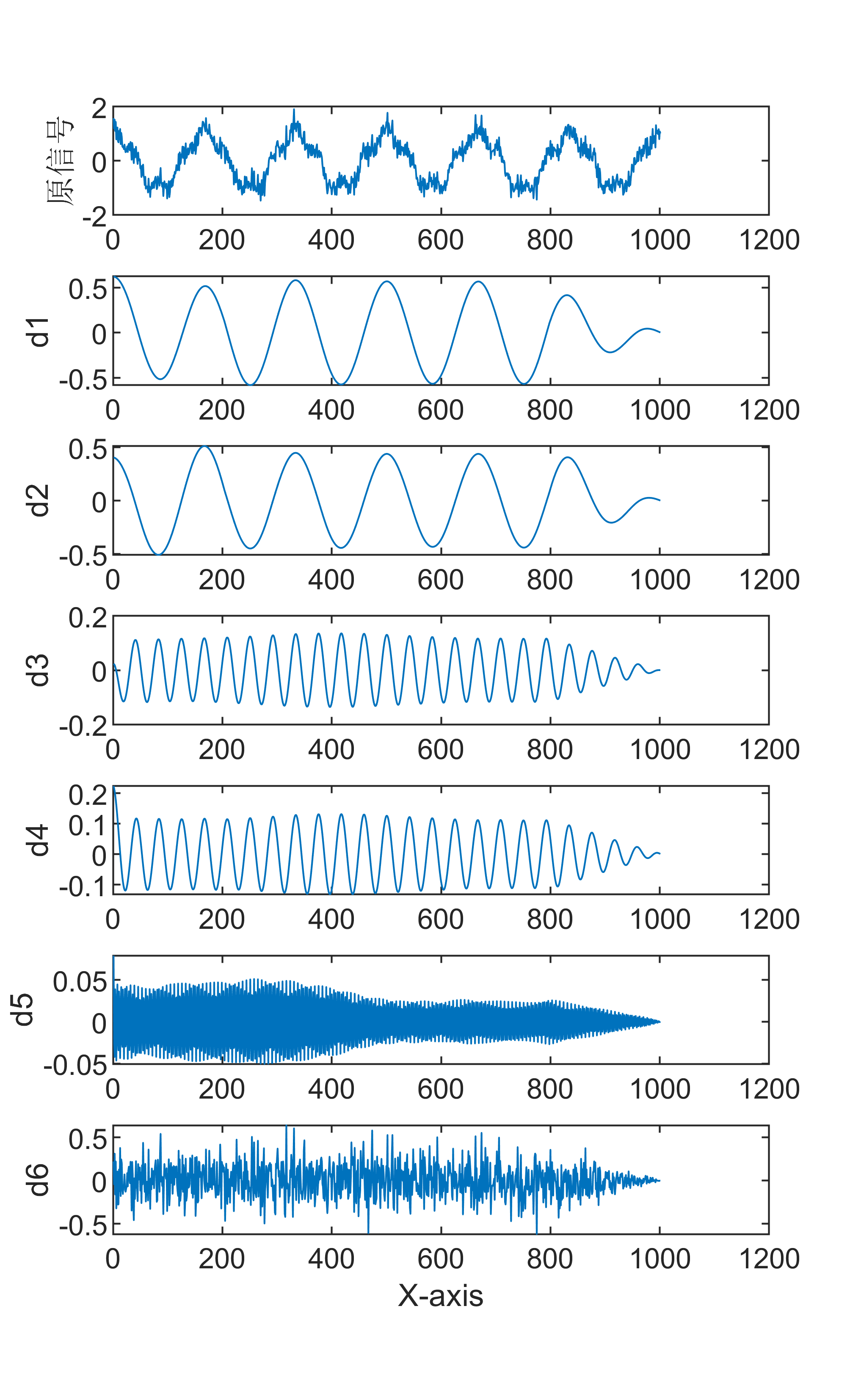
【MATLAB】全网唯一的13种信号分解+FFT傅里叶频谱变换联合算法全家桶
有意向获取代码,请转文末观看代码获取方式~ 大家吃一顿火锅的价格便可以拥有13种信号分解FFT傅里叶频谱变换联合算法,绝对不亏,知识付费是现今时代的趋势,而且都是我精心制作的教程,有问题可随时反馈~也可单独获取某一…...
Nginx安装与配置
1.下载安装包 官网下载地址:nginx: download 可以先将安装包下载到本地再传到服务器,或者直接用wget命令将安装包下载到服务器,这里我们直接将安装包下载到服务器上。未安装wget命令的需要先安装wget,yum install -y wget [root…...

linux笔记总结-基本命令
参考: 1.Linux 和Windows比 比较 (了解) 1. 记住一句经典的话:在 Linux 世界里,一切皆文件 2. Linux目录结构 /lib • 系统开机所需要最基本的动态连接共享库,其作用类似于Windows里的DLL文件。几 乎所有…...
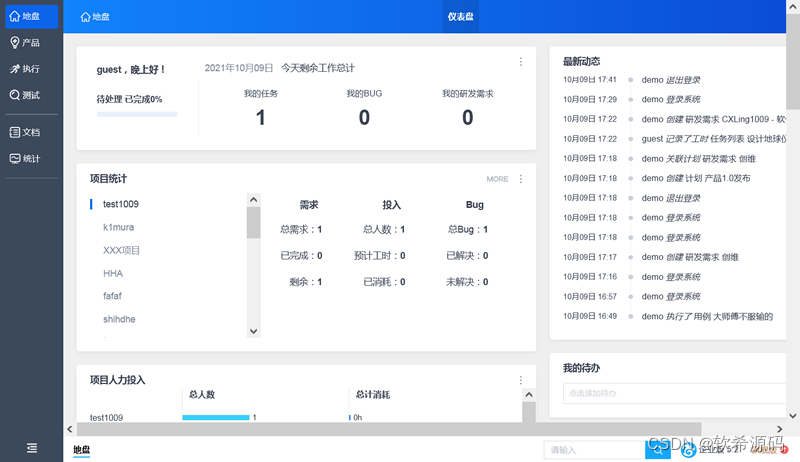
[PHP]禅道项目管理软件ZenTaoPMS源码包 v16.4
禅道项目管理软件ZenTaoPMS一键安装包是一款国产的开源项目管理软件。它集产品管理、项目管理、质量管理、文档管理、组织管理和事务管理于一体,是一款专业的研发项目管理软件,完整地覆盖了项目管理的核心流程。注重实效的管理思想,合理的软件…...

Required String parameter ‘name‘ is not present
[org.springframework.web.bind.MissingServletRequestParameterException: Required String parameter name is not present] 服务端有参数name,客户端没有传上来...
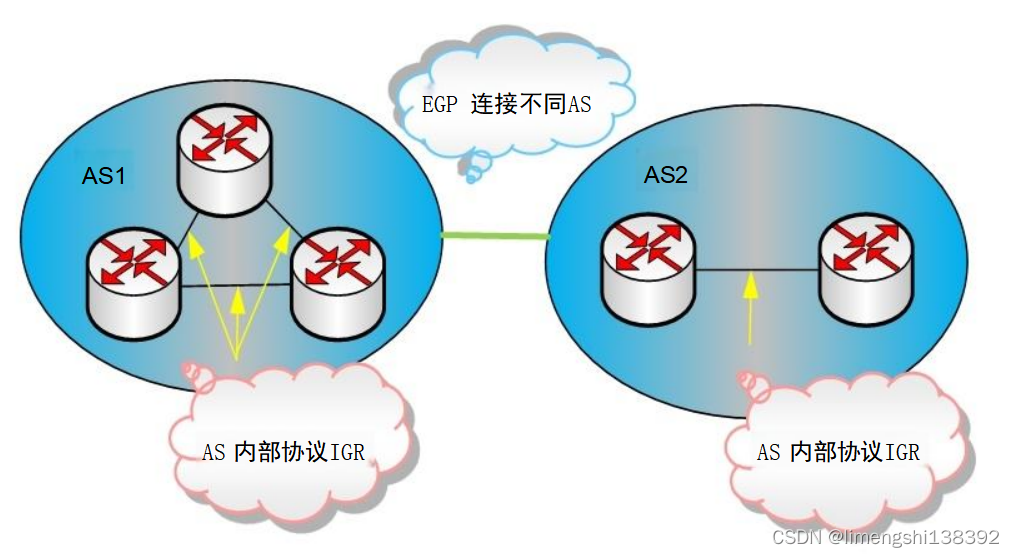
路由器基础(五): OSPF原理与配置
开放式最短路径优先 (Open Shortest Path First,OSPF) 是一个内部网关协议 (Interior Gateway Protocol,IGP),用于在单一自治系统(Autonomous System,AS) 内决策路由。OSPF 适合小型、中型、较大规模网络。OSPF 采用Dijkstra的最短路径优先算法 (Shortest Pat…...
Leetcode1128. 等价多米诺骨牌对的数量
Every day a Leetcode 题目来源:1128. 等价多米诺骨牌对的数量 解法1:暴力 代码: class Solution { public:int numEquivDominoPairs(vector<vector<int>> &dominoes){int n dominoes.size(), count 0;for (int i 0;…...
Dev-C调试的基本方法2-2
3.3 跳出函数 在图6所示的状态下,点击单步调试(F7)会继续调试下一行,而如果想结束在函数中的调试,则点击图4③所示的跳出函数,或CtrlF8按键跳出f()函数,程序将会停在图5所示的第11行处。 3.4 …...

基于Flask实现的医疗保险欺诈识别监测模型
基于Flask实现的医疗保险欺诈识别监测模型 项目截图 项目简介 社会医疗保险是国家通过立法形式强制实施,由雇主和个人按一定比例缴纳保险费,建立社会医疗保险基金,支付雇员医疗费用的一种医疗保险制度, 它是促进社会文明和进步的…...

Matlab | matlab常用命令总结
常用命令 一、 基础操作与环境二、 矩阵与数组操作(核心)三、 绘图与可视化四、 编程与控制流五、 符号计算 (Symbolic Math Toolbox)六、 文件与数据 I/O七、 常用函数类别重要提示这是一份 MATLAB 常用命令和功能的总结,涵盖了基础操作、矩阵运算、绘图、编程和文件处理等…...

【JavaSE】绘图与事件入门学习笔记
-Java绘图坐标体系 坐标体系-介绍 坐标原点位于左上角,以像素为单位。 在Java坐标系中,第一个是x坐标,表示当前位置为水平方向,距离坐标原点x个像素;第二个是y坐标,表示当前位置为垂直方向,距离坐标原点y个像素。 坐标体系-像素 …...

无人机侦测与反制技术的进展与应用
国家电网无人机侦测与反制技术的进展与应用 引言 随着无人机(无人驾驶飞行器,UAV)技术的快速发展,其在商业、娱乐和军事领域的广泛应用带来了新的安全挑战。特别是对于关键基础设施如电力系统,无人机的“黑飞”&…...

Python 实现 Web 静态服务器(HTTP 协议)
目录 一、在本地启动 HTTP 服务器1. Windows 下安装 node.js1)下载安装包2)配置环境变量3)安装镜像4)node.js 的常用命令 2. 安装 http-server 服务3. 使用 http-server 开启服务1)使用 http-server2)详解 …...

Proxmox Mail Gateway安装指南:从零开始配置高效邮件过滤系统
💝💝💝欢迎莅临我的博客,很高兴能够在这里和您见面!希望您在这里可以感受到一份轻松愉快的氛围,不仅可以获得有趣的内容和知识,也可以畅所欲言、分享您的想法和见解。 推荐:「storms…...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

LOOI机器人的技术实现解析:从手势识别到边缘检测
LOOI机器人作为一款创新的AI硬件产品,通过将智能手机转变为具有情感交互能力的桌面机器人,展示了前沿AI技术与传统硬件设计的完美结合。作为AI与玩具领域的专家,我将全面解析LOOI的技术实现架构,特别是其手势识别、物体识别和环境…...

DeepSeek源码深度解析 × 华为仓颉语言编程精粹——从MoE架构到全场景开发生态
前言 在人工智能技术飞速发展的今天,深度学习与大模型技术已成为推动行业变革的核心驱动力,而高效、灵活的开发工具与编程语言则为技术创新提供了重要支撑。本书以两大前沿技术领域为核心,系统性地呈现了两部深度技术著作的精华:…...

[特殊字符] 手撸 Redis 互斥锁那些坑
📖 手撸 Redis 互斥锁那些坑 最近搞业务遇到高并发下同一个 key 的互斥操作,想实现分布式环境下的互斥锁。于是私下顺手手撸了个基于 Redis 的简单互斥锁,也顺便跟 Redisson 的 RLock 机制对比了下,记录一波,别踩我踩过…...
