怎样选择文件外发控制系统,让数据实现高效安全交换?
制造型企业都非常重视其知识产权(IP)的安全性,尤其是其最有价值的产品设计数据的安全问题。基于复杂的供应链生态,每天可能要与几十家甚至上百家供应商及合作伙伴进行数据交换。不管是一级还是二级供应商,合作伙伴还是原始设备制造商(OEM),频繁的业务协作都会为数据交换过程带来风险,因此需要一个文件外发控制系统,来进行数据的安全交换。

确保产品数据传输过程的安全,是整个安全策略中最明显也最重要的步骤。企业如何处理和交换,所有项目中与合作伙伴的产品设计数据,将这一过程标准化,由系统预制的安全策略进行统一控制。同时,摒除非监管范围内的非合规交换手段,比如邮件、FTP、网络共享等方式,消除高风险的数据交换渠道。
以FTP举例,一直以来使用比较广泛。操作比较简单,可以传输多个文件,还可以同时传输多个目录。支持多任务处理,可以上传已完成的任何任务,同时下载计划开始工作的任务。但其凸显出来的缺点也是不容忽视的。
1.安全性低:FTP客户端ID和密码以明文传输,易于被截获和窃取
2.可靠性差:传输性能差,无法即时通知和处理传输异常,直到业务失败,问题才被发现,甚至从客户那里获知
3.缺乏可见性:无审核审批,数据流向不可控,出现问题难以追溯
4.难以运维:账号发放和回收,临时的权限调整。被迫管理越来越多的服务器节点
因此,企业需要有一个专业的外发平台,让企业和外部进行安全可控的文件交换,功能上至少需要做到以下几点:要有审批,需要通过各种安全策略保护数据,比如传输加密、存储加密等;对发出去的文件进行加密保护,限制打开次数、获取密码、截止日期、禁止的操作等,从而杜绝二次泄密;能即时通知和处理传输异常,比如断点续传、错误重传,传输完整性100%;需要经过审批后实现安全合规的发送;要有完整的日志记录,所有的操作行为以及文件内容都要能审计追溯。
《Ftrans文件安全收发系统》,可以帮助企业建立安全合规、高效可靠的文件收发统一通道,在一个平台内,自动化地完成文件发送、内容安全检查、审核审批、消息通知、文件提取、归档销毁、历史审计的完整业务过程,大幅提升操作易用性及业务时效性,实现了对文件外发全生命周期的可见性。我们来看看这套文件外发控制系统有哪些功能特点:
1、重要文件外发,必须经过领导审批
支持多级、多人审批,会签、或签,确保文件外发安全合规。基于文件属性、收发件人特征等条件,自定义自动发起文件审批流程。可与外部审批系统集成(OA、BPM),实现文件外发和审批一体化。支持邮件审批、移动审批、企业微信审批,让审批操作更便捷。
2、不限大小,不限速度,大附件收发超顺畅
不限文件大小、数量,高效稳定上传下载,不改变邮件使用习惯,操作使用简便。支持Outlook、OWA、Exchange,使用无门槛。
3、全平台日志审计全掌握
根据完整的日志记录,形成报表,便于灵活查询。不仅可以审计操作记录,还能审计原始文件。文件包创建、发送、审批、访问、下载,均有记录以备审计。
4、灵活的文件共享协作
符合项目制的协同工作模式,支持团队协作和共享。网盘模式的个人文件夹或共享文件夹上传,一对多的邮件群发。临时伙伴无需创建账号,通过分享链接方式交换数据。
5、大体量业务数据高速可靠交换
完美解决生产、研发、测试类等大体量业务数据的跨网交换难题。内置高性能传输协议,带宽利用率可达80%以上,极大提升业务时效性。断点续传、自动重传、完整性校验,100%保证文件正确性。
在未来的发展中,这款文件外发控制系统还将继续不断完善,为企业提供更加高效、安全的数据传输解决方案,成为企业保障数据传输安全的关键因素。
相关文章:

怎样选择文件外发控制系统,让数据实现高效安全交换?
制造型企业都非常重视其知识产权(IP)的安全性,尤其是其最有价值的产品设计数据的安全问题。基于复杂的供应链生态,每天可能要与几十家甚至上百家供应商及合作伙伴进行数据交换。不管是一级还是二级供应商,合作伙伴还是…...

专访 SPACE ID:通往 Web3 无许可域名服务协议之路
Web3 行业发展风起云涌,对于初创项目而言,如何寻找适合自己的赛道是首要问题。当前伴随用户交互和跨平台操作需求日渐兴起,如何更迅速地使用一站式域名实现便捷验证成为大众的心头期盼。 这一背景下,SPACE ID 于众星林立的 Web3 …...

合并分支--将自己的分支合并到master分支
在版本控制系统(例如Git)中,将自己的分支合并到master(或者主分支)通常需要以下步骤: ### 1. 切换到主分支 首先,确保你的本地仓库当前处于主分支。你可以使用以下命令切换到主分支࿱…...
)
力扣:153. 寻找旋转排序数组中的最小值(Python3)
题目: 已知一个长度为 n 的数组,预先按照升序排列,经由 1 到 n 次 旋转 后,得到输入数组。例如,原数组 nums [0,1,2,4,5,6,7] 在变化后可能得到: 若旋转 4 次,则可以得到 [4,5,6,7,0,1,2]若旋转…...
matlab中实现画函数图像添加坐标轴
大家好,我是带我去滑雪! 主函数matlab代码: function PlotAxisAtOrigin(x,y); if nargin 2 plot(x,y);hold on; elsedisplay( Not 2D Data set !) end; Xget(gca,Xtick); Yget(gca,Ytick); XLget(gca,XtickLabel); YLget(gca,YtickLabel)…...
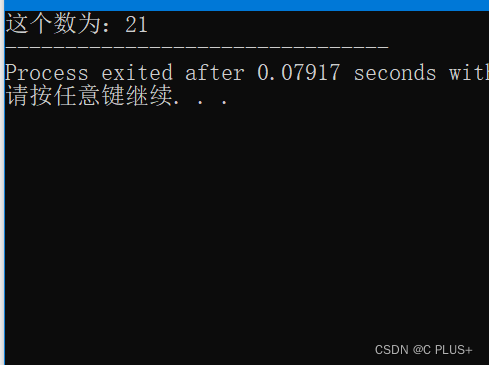
C语言求解一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问该数是多少?
完整代码: /* 一个整数,它加上100后是一个完全平方数,再加上168又是一个完全平方数,请问 该数是多少?*/ #include<stdio.h>int main(){//num为最终所求那个数int num;//i*i为第一个完全平方数for (int i 10; …...

AtCoder abc148
C题 求GCD D题 顺序遍历 E题 trailing zero只与5的个数有关,因此算一下5/25/125…的倍数 # -*- coding: utf-8 -*- # time : 2023/6/2 13:30 # file : atcoder.py # software : PyCharmimport bisect import copy import sys from itertools import perm…...

k8s、docker 卸载
k8s卸载 k8s 重置 kubeadm reset -f如果kubernets是1.24以上版本,请先单独卸载containerd sudo apt purge containerd.iok8s软件卸载 ubuntu #apt卸载 apt purge kubelet kubeadm kubectlcentos yum erase -y kubelet kubectl kubeadm 删除kubelet相关信息&am…...
【Linux】Shell命令行的简易实现(C语言实现)内键命令,普通命令
文章目录 0.准备工作1.大体框架 一、获取命令行二、解析命令行三、进程执行1.普通命令2.内建命令 四、完整代码: 0.准备工作 1.大体框架 #include <stdio.h> #include <stdlib.h> #include <string.h> #include <assert.h> #include <u…...
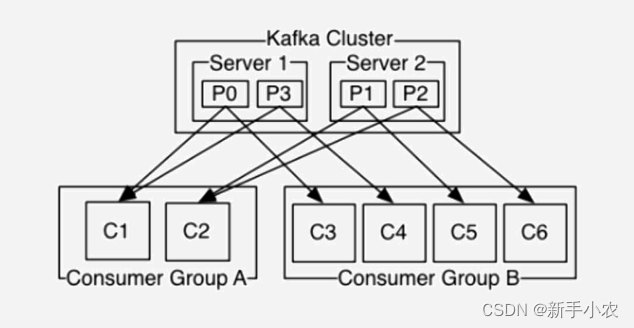
Kafka -- 架构、分区、副本
1、Kafka的架构: 1、producer:消息的生产者 2、consumer:消息的消费者 3、broker:kafka集群的服务者,一个broker就是一个节点,主要是负责处理消息的读、写的请求和存储消息。在kafka cluster中包含很多的br…...

CSS特效001:鼠标放div上,实现旋转、放大、移动等效果
GPT能够很好的应用到我们的代码开发中,能够提高开发速度。你可以利用其代码,做出一定的更改,然后实现效能。 css实战中,经常会看到这样的场景,鼠标放到一个图片或者一个div块状时候,会出现旋转、放大、移动…...

gin 快速入门手册
文章目录 安装URL和路由分组2. 带参数的url3. 获取路由分组的参数 获取参数1. 获取get参数2. 获取post参数3. get、post混合 JSON 、 ProtoBuf渲染1. 输出json和protobuf2. PureJSON 表单验证1. 表单的基本验证 中间件和next函数1. 无中间件启动2. 使用中间件3. 自定义组件 设置…...
Window下安装 Mongodb,并实现单点事务
在window操作系统下安装Mongodb,并让单点mongodb支持事务,mongodb5以上时才支持事务,所以必须时mongodb5及以上版本才支持。 1、下载mongodb安装文件 (1) 下载mongodb msi 安装文件 地址:mongocommunity &…...

【通信原理】第三章 随机过程——例题
一、随机过程 1. 数学特征 ① 随机信号(三角函数表达式) ② 随机信号(求和表达式) 2. 功率谱密度 ① 相位确定,求功率谱密度 ② 已知相位分布,求功率谱密度 ③ 信号为两信号之和,求功率谱密度…...
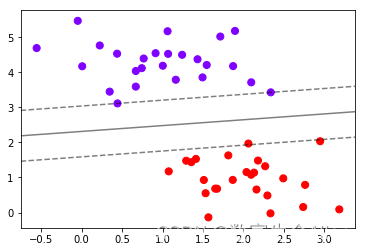
线性【SVM】数学原理和算法实现
一. 数学原理 SVM是一类有监督的分类算法,它的大致思想是:假设样本空间上有两类点,如下图所示,我们希望找到一个划分超平面,将这两类样本分开,我们希望这个间隔能够最大化来使得模型泛化能力最强。 如上图所…...

R语言中的函数26:polyroot多项式求根函数
目录 介绍函数介绍参数含义 示例 介绍 R语言中的base::polyroot()可以用于对多项式求根,求根的多项式可以是复数域上的。 函数介绍 polyroot(z)该函数利用Jenkins-Traub算法对多项式 p ( x ) p(x) p(x)进行求根,其中 p ( x ) z 1 z 2 x ⋯ z n x…...

2023年辽宁省数学建模竞赛A题铁路车站的安全标线
2023年辽宁省数学建模竞赛 A题 铁路车站的安全标线 原题再现: 在火车站或地铁站台上,离站台边缘 1 米左右的地方都画有一条黄线(或白线),这是为什么呢? 这条线称为安全线(业内称之为安全标线),人们在候车时必须站在安全线以…...

半导体工厂将应用哪些制造创新技术?
半导体工厂是高科技产业的结晶,汇聚了世界上最新的技术。 在半导体的原料硅晶片上绘制设计图纸,不产生误差,准确切割并包装,然后用芯片生产出我们使用的电脑、智能手机、手表等各种电子产品。绝大多数半导体厂都采用一贯的工艺&a…...
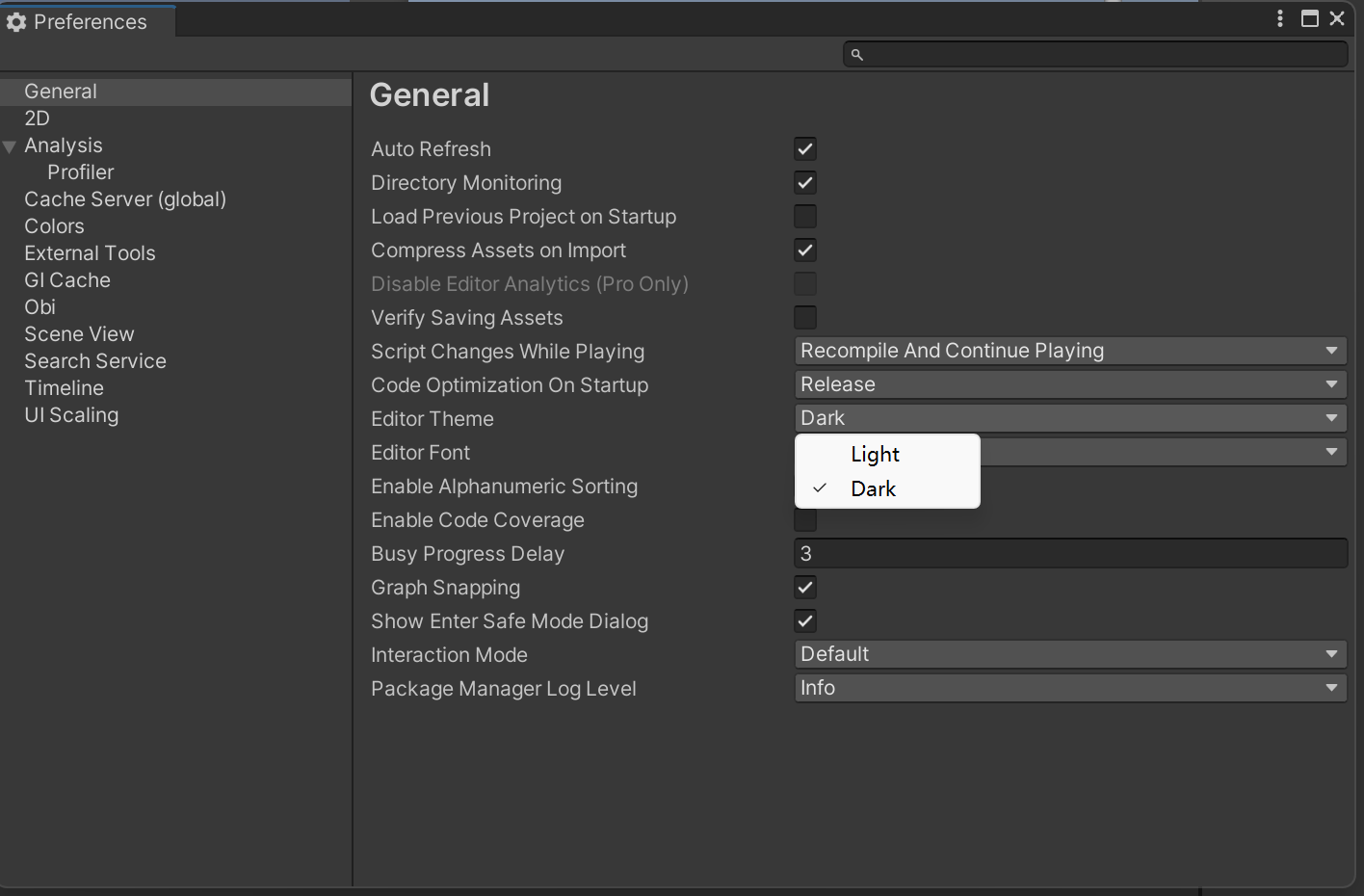
[unity]深色模式/浅色模式
这里用的是Windows版的unity,具体版本号如下: 选项的路径如下:Edit—Preferences—General—Editor Theme 然后就可以选是dark还是light了:...
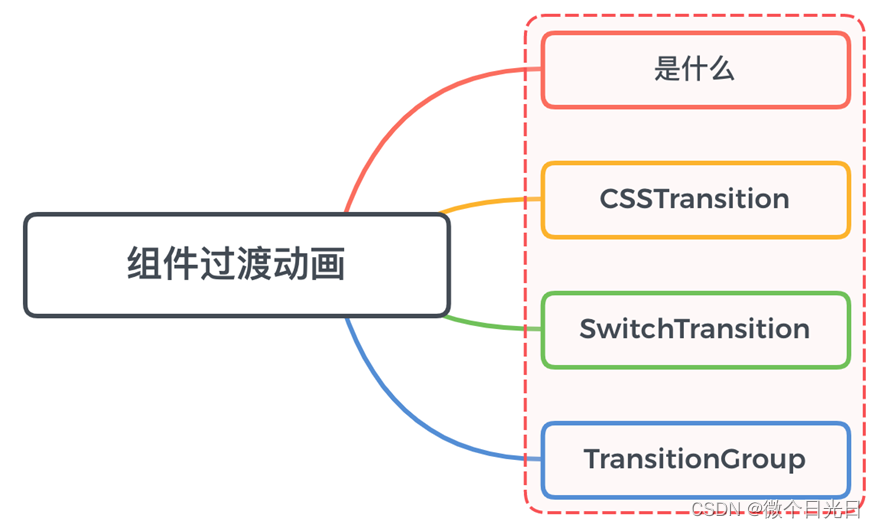
在react中组件间过渡动画如何实现?
一、是什么 在日常开发中,页面切换时的转场动画是比较基础的一个场景 当一个组件在显示与消失过程中存在过渡动画,可以很好的增加用户的体验 在react中实现过渡动画效果会有很多种选择,如react-transition-group,react-motion&…...

C++初阶-list的底层
目录 1.std::list实现的所有代码 2.list的简单介绍 2.1实现list的类 2.2_list_iterator的实现 2.2.1_list_iterator实现的原因和好处 2.2.2_list_iterator实现 2.3_list_node的实现 2.3.1. 避免递归的模板依赖 2.3.2. 内存布局一致性 2.3.3. 类型安全的替代方案 2.3.…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

3.3.1_1 检错编码(奇偶校验码)
从这节课开始,我们会探讨数据链路层的差错控制功能,差错控制功能的主要目标是要发现并且解决一个帧内部的位错误,我们需要使用特殊的编码技术去发现帧内部的位错误,当我们发现位错误之后,通常来说有两种解决方案。第一…...
` 方法)
深入浅出:JavaScript 中的 `window.crypto.getRandomValues()` 方法
深入浅出:JavaScript 中的 window.crypto.getRandomValues() 方法 在现代 Web 开发中,随机数的生成看似简单,却隐藏着许多玄机。无论是生成密码、加密密钥,还是创建安全令牌,随机数的质量直接关系到系统的安全性。Jav…...

DIY|Mac 搭建 ESP-IDF 开发环境及编译小智 AI
前一阵子在百度 AI 开发者大会上,看到基于小智 AI DIY 玩具的演示,感觉有点意思,想着自己也来试试。 如果只是想烧录现成的固件,乐鑫官方除了提供了 Windows 版本的 Flash 下载工具 之外,还提供了基于网页版的 ESP LA…...
)
【服务器压力测试】本地PC电脑作为服务器运行时出现卡顿和资源紧张(Windows/Linux)
要让本地PC电脑作为服务器运行时出现卡顿和资源紧张的情况,可以通过以下几种方式模拟或触发: 1. 增加CPU负载 运行大量计算密集型任务,例如: 使用多线程循环执行复杂计算(如数学运算、加密解密等)。运行图…...

3403. 从盒子中找出字典序最大的字符串 I
3403. 从盒子中找出字典序最大的字符串 I 题目链接:3403. 从盒子中找出字典序最大的字符串 I 代码如下: class Solution { public:string answerString(string word, int numFriends) {if (numFriends 1) {return word;}string res;for (int i 0;i &…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

人工智能(大型语言模型 LLMs)对不同学科的影响以及由此产生的新学习方式
今天是关于AI如何在教学中增强学生的学习体验,我把重要信息标红了。人文学科的价值被低估了 ⬇️ 转型与必要性 人工智能正在深刻地改变教育,这并非炒作,而是已经发生的巨大变革。教育机构和教育者不能忽视它,试图简单地禁止学生使…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...
