2023NOIP A层联测27 总结
T1 一棵树,操作是把一个点染黑,查询点 x x x 到黑点路径上的最小编号, n ≤ 1 0 6 n\le10^6 n≤106。当时的思路是把树分成几部分,中间和周围的散块,发现不会,就没思路了,就去打了25pts暴力。赛后发现55pts暴力很简单,真遗憾没去打。题解方法很巧妙,设了装置为根,又维护点到根的最小编号,tql。
T2 一棵树,有若干棋子,每次操作把两个棋子相互靠近一步,问是否能把所有棋子移到同一点上, n ≤ 1 0 6 n\le10^6 n≤106。分析了性质发现,对于一个点,只有有棋子的点到它的距离之和为偶数,才可能有解。然后就不知道接下来怎么判断,就打了个假的贪心,取可能有解的最小距离除以2为答案,喜提71pts。题解是换根dp,写法很复杂。
T3 随机生成 n n n 个长度为 a i a_i ai 的小写字母串, f ( s ) f(s) f(s) 表示 s s s 的最小表示的开头字符在 s s s 的下标,取最小的,求 ∑ i = 1 n [ f ( s i ) = f ( s i m o d n + 1 ) ] \sum\limits_{i=1}^n[f(s_i)=f(s_{i\bmod n+1})] i=1∑n[f(si)=f(simodn+1)]。看错题了,以为求最小的字符的下标,就用了1h+思考写代码,搞了半天过不了样例。赛后看懂题后发现,哎,真遗憾。
T4 树上有一条蛇,移动时身体不能重合,问是否能够头尾互换。题目很抽象,没看懂。发现题解又是换根,还要讨论一大堆,不过思路挺清晰,洛谷上是黑题,感觉最多紫。
期望得分:25+?+0+0=25+?
实际得分:25+71+0+0=96
总结:这场比赛在我看来比较难,导致我的心态不好,不想做,部分分都没有精力去骗,考试策略没有严格执行。对于解决树上问题不能熟练润用。要仔细看题目,正确理解题意。无根树转有根树,再维护到根的信息,可能有大用,树型dp继续优化多半是换根。考前要休息好。
相关文章:

2023NOIP A层联测27 总结
T1 一棵树,操作是把一个点染黑,查询点 x x x 到黑点路径上的最小编号, n ≤ 1 0 6 n\le10^6 n≤106。当时的思路是把树分成几部分,中间和周围的散块,发现不会,就没思路了,就去打了25pts暴力。赛…...
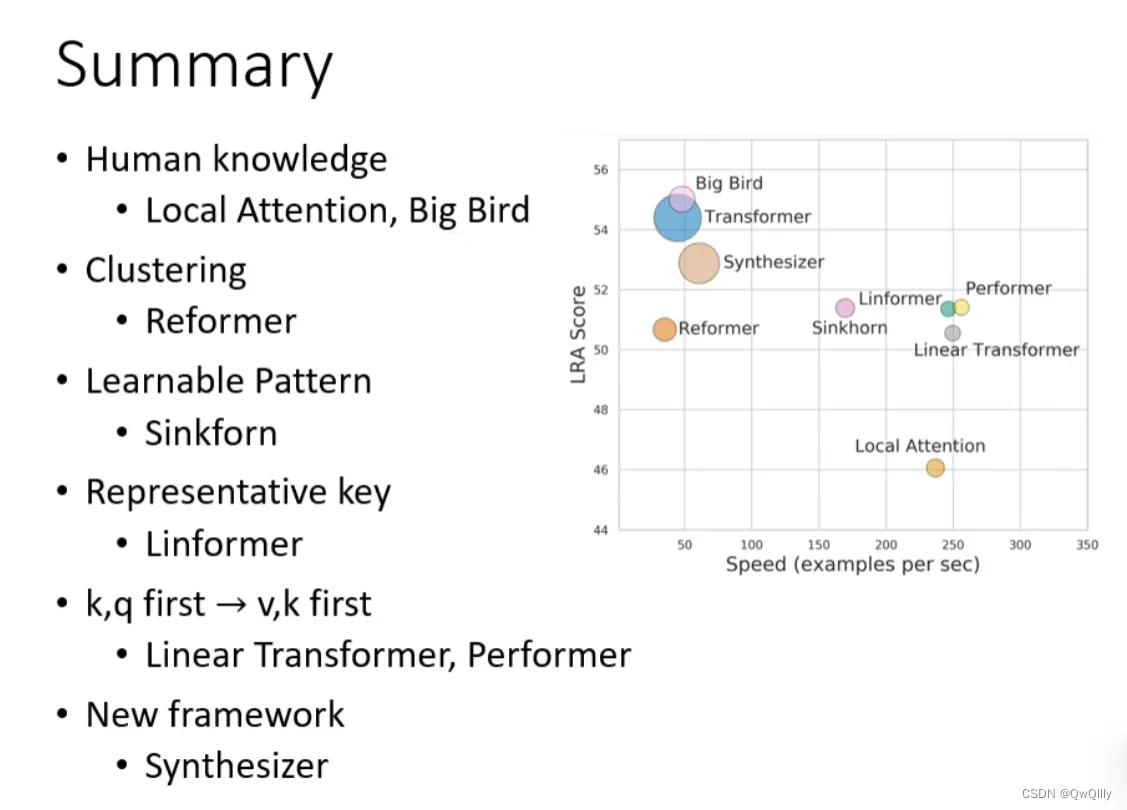
2022最新版-李宏毅机器学习深度学习课程-P34 自注意力机制类别总结
在课程的transformer视频中,李老师详细介绍了部分self-attention内容,但是self-attention其实还有各种各样的变化形式: 一、Self-attention运算存在的问题 在self-attention中,假设输入序列(query)长度是N…...
css sprite 的优缺点,使用方法和示例
CSS Sprite是一种网页图片应用处理方式。 CSS Sprite的原理是将一个网页或者一个模块所用到的零碎的icon整合拼接到一张大图里,再把这张大图作为背景图放入到网页中,当访问该页面时,加载的图片就不会像以前那样一幅一幅地慢慢显示出来了。 …...
通过Cookie和Session来实现网站中登录账号的功能
文章目录 一、Cookie和Session二、基于Cookie和Session实现登录账号的功能2.1步骤一2.2步骤二2.3步骤三2.4总结通过Cookie和Session来实现登录功能2.5运行截图 一、Cookie和Session cookie是http请求header中的一个属性,是浏览器持久化存储数据的一种机制ÿ…...

QWidget 实现九宫格图案解锁
前言 最近需要实现一个九宫格图案解锁功能,查看网上的方案,基于QWidget的方案全网搜来搜去就一篇 Qt编写自定义控件:图案密码锁, 都是炒来炒去的同一篇,代码还比较复杂,运行后在PC端还是可以的,但是运行在arm机器上,就卡顿,或者容易断开手势连接线,各种不友好,于是自…...
)
设计模式-适配器模式(Adapter)
设计模式-适配器模式(Adapter) 一、适配器模式概述1.1 什么是适配器模式1.2 简单实现适配器模式1.3 使用适配器模式注意事项 二、适配器模式的用途三、实现适配器模式的方式3.1 继承适配器模式(Inheritance Adapter)3.2 组合适配器…...

react:创建项目
一: 使用create-react-app // 默认创建reactjs的webpack打包项目 npm i create-react-app -g create-react-app 项目名// 创建ts项目打包项目 sudo npx create-react-app my-app --template typescript 二: 使用vite npm create vitelatest // 创建react…...
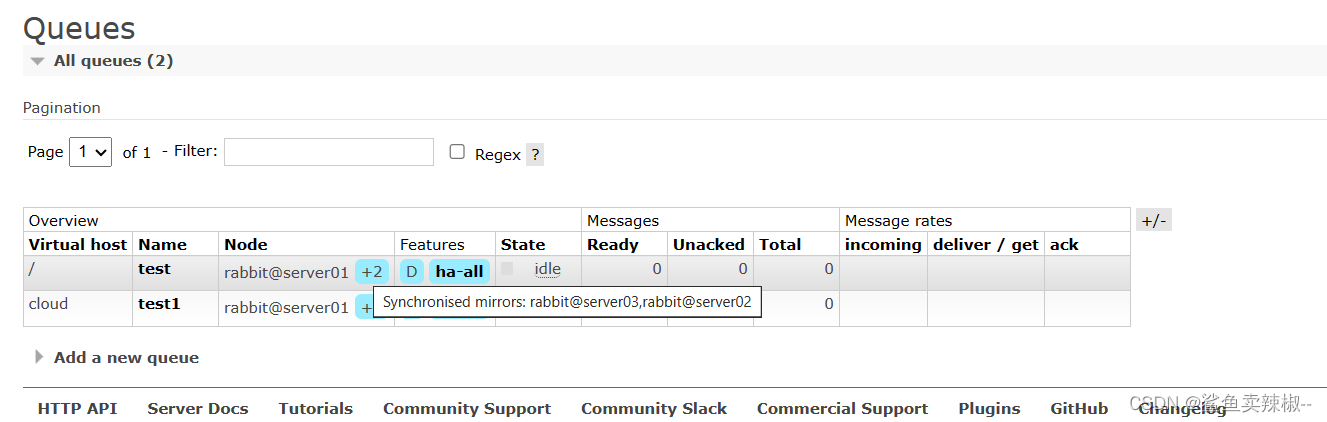
RabbitMQ集群
RabbitMQ概述 1.RabbiMQ简介 RabbiMQ是⽤Erang开发的,集群⾮常⽅便,因为Erlang天⽣就是⼀⻔分布式语⾔,但其本身并不⽀持负载均衡。支持高并发,支持可扩展。支持AJAX,持久化,用于在分布式系统中存储转发消…...

Qt QtCreator调试Qt源码配置
目录 前言1、编译debug版Qt2、QtCreator配置3、调试测试4、总结 前言 本篇主要介绍了在麒麟V10系统下,如何编译debug版qt,并通过配置QtCreator实现调试Qt源码的目的。通过调试源码,我们可以对Qt框架的运行机制进一步深入了解,同时…...

JavaScript如何实现钟表效果,时分秒针指向当前时间,并显示当前年月日,及2024春节倒计时,源码奉上
本篇有运用jQuery,记得引入jQuery库,否则不会执行的喔~ <!DOCTYPE html> <html> <head> <meta charset"utf-8"> <title></title> <meta name"chenc" content"Runoob"> <met…...
重生奇迹MU套装大全中的极品属性
在重生奇迹MU之中,你不能如其他游戏一般只看攻击与防御,你更要看属性,这才是重生奇迹中的王道!属性好,才是极品,属性不佳,即便攻击、防御再出色,也只能沦落成为一件替用品࿰…...

用Python解决猴子分桃问题
1 问题 海滩上有一堆桃子,五只猴子来分。第一只猴子把这堆桃子平均分为五份,多了一个,这只猴子把多的一个扔入海中,拿走了一份。第二只猴子把剩下的桃子又平均分成五份,又多了一个,它同样把多的一个扔入海中…...

YOLOv8-Seg改进:分割注意力系列篇 | 新型的多尺度卷积注意力(MSCA)模块
🚀🚀🚀本文改进: 新型的多尺度卷积注意力(MSCA)模块,实现创新,MSCA包含三个部分:深度卷积聚合局部信息,多分支深度条卷积捕获多尺度上下文,以及11卷积建模不同通道之间的关系。 🚀🚀🚀MSCA多尺度特性在小目标分割检测领域表现优异 🚀🚀🚀YOLOv8-seg…...

基于springboot实现致远汽车租赁平台管理系统项目【项目源码+论文说明】计算机毕业设计
基于springboot实现致远汽车租赁平台管理系统演示 摘要 首先,论文一开始便是清楚的论述了系统的研究内容。其次,剖析系统需求分析,弄明白“做什么”,分析包括业务分析和业务流程的分析以及用例分析,更进一步明确系统的需求。然后在明白了系统的需求基础上需要进一步地设计系统…...
真的设计师做图只需要一个炫云客户端就够了
真的设计师做图只需要一个炫云客户端就够了,为什么这么说呢?因为炫云的这个客户端功能真的太全了,设计师想要的功能在炫云客户端上都有,而且还很多功能是免费的,非常的实用,具体有哪些功能我们一起来看看吧…...

简述 HTTP 请求的过程是什么?
HTTP(Hypertext Transfer Protocol)请求的过程可以简单地描述为客户端与服务器之间的通信交互。下面是一般的 HTTP 请求过程: 解析 URL:客户端解析目标 URL,提取出服务器的主机名(域名)和端口号…...

免root修改手机imei的技术原理是什么?如何实现的?hook吗
在过去,修改手机IMEI(International Mobile Equipment Identity)通常需要Root权限,这给用户带来了一些不便,也存在一定的安全风险。然而,近年来,一些技术爱好者提出了一种免Root修改手机IMEI的方…...

【Redis】整合使用,进行注解式开发及应用场景和击穿、穿透、雪崩的讲解
目录 一、整合 1. 为什么 2. 整合应用 ( 1 ) pom配置 ( 2 ) 所需配置 3. 注解式开发及应用场景 1. Cacheable 2. CachePut 3. CacheEvict 4. 击穿、穿透、雪崩 一、整合 1. 为什么 Redis可以与SSM项目整合,主要是为了提高项目的性能和效率。以下是整合Re…...
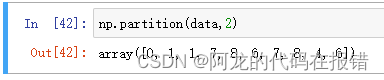
数据分析-numpy
numpy numpy numpy简介优点下载ndarray的属性输出数据类型routines 函数ndarray对象的读写操作ndarray的级联和切分级联切分 ndarray的基本运算广播机制(Broadcast)ndarry的聚合操作数组元素的操作numpy 数学函数numpy 查找和排序 写在最后面 简介 nump…...
【Java】云HIS云端数字医院信息平台源码
一、云HIS系统特色 • 使用简易化 即开即用,快速复制,按需开通功能模块,多机构共享机房、软件、服务器、存储设备等资源,资源利用最大化。 • 连锁集团化 可支持连锁集团化管理,1N模式,支撑运营&#x…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

数据链路层的主要功能是什么
数据链路层(OSI模型第2层)的核心功能是在相邻网络节点(如交换机、主机)间提供可靠的数据帧传输服务,主要职责包括: 🔑 核心功能详解: 帧封装与解封装 封装: 将网络层下发…...

中医有效性探讨
文章目录 西医是如何发展到以生物化学为药理基础的现代医学?传统医学奠基期(远古 - 17 世纪)近代医学转型期(17 世纪 - 19 世纪末)现代医学成熟期(20世纪至今) 中医的源远流长和一脉相承远古至…...

iview框架主题色的应用
1.下载 less要使用3.0.0以下的版本 npm install less2.7.3 npm install less-loader4.0.52./src/config/theme.js文件 module.exports {yellow: {theme-color: #FDCE04},blue: {theme-color: #547CE7} }在sass中使用theme配置的颜色主题,无需引入,直接可…...
)
uniapp 集成腾讯云 IM 富媒体消息(地理位置/文件)
UniApp 集成腾讯云 IM 富媒体消息全攻略(地理位置/文件) 一、功能实现原理 腾讯云 IM 通过 消息扩展机制 支持富媒体类型,核心实现方式: 标准消息类型:直接使用 SDK 内置类型(文件、图片等)自…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

GraphRAG优化新思路-开源的ROGRAG框架
目前的如微软开源的GraphRAG的工作流程都较为复杂,难以孤立地评估各个组件的贡献,传统的检索方法在处理复杂推理任务时可能不够有效,特别是在需要理解实体间关系或多跳知识的情况下。先说结论,看完后感觉这个框架性能上不会比Grap…...
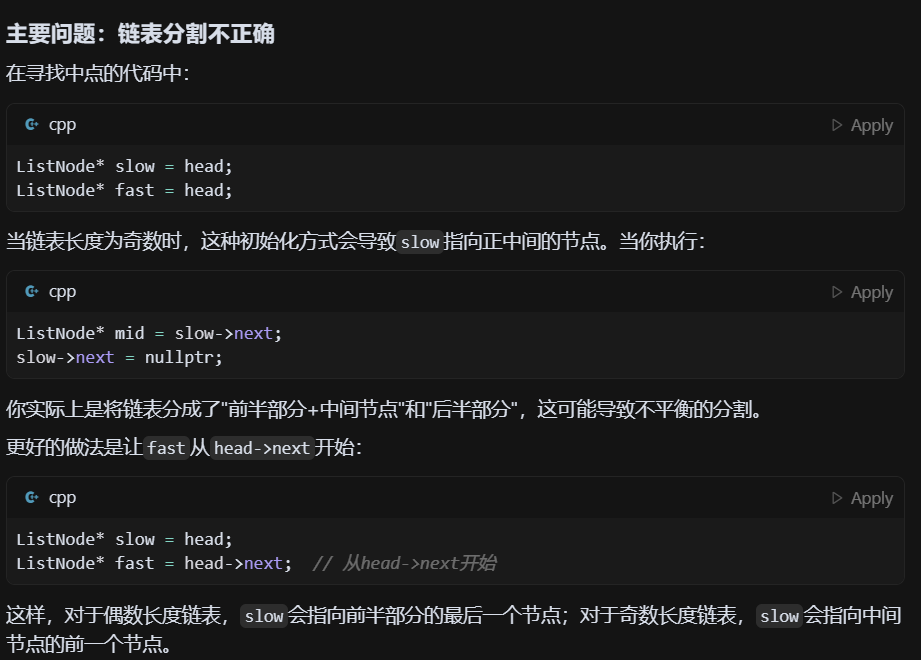
LeetCode - 148. 排序链表
目录 题目 思路 基本情况检查 复杂度分析 执行示例 读者可能出的错误 正确的写法 题目 148. 排序链表 - 力扣(LeetCode) 思路 链表归并排序采用"分治"的策略,主要分为三个步骤: 分割:将链表从中间…...

Unity-ECS详解
今天我们来了解Unity最先进的技术——ECS架构(EntityComponentSystem)。 Unity官方下有源码,我们下载源码后来学习。 ECS 与OOP(Object-Oriented Programming)对应,ECS是一种完全不同的编程范式与数据架构…...
)
Spring Boot 与 Kafka 的深度集成实践(二)
3. 生产者实现 3.1 生产者配置 在 Spring Boot 项目中,配置 Kafka 生产者主要是配置生产者工厂(ProducerFactory)和 KafkaTemplate 。生产者工厂负责创建 Kafka 生产者实例,而 KafkaTemplate 则是用于发送消息的核心组件&#x…...
