线性代数(五) | 矩阵对角化 特征值 特征向量
文章目录
- 1 矩阵的特征值和特征向量究竟是什么?
- 2 求特征值和特征向量
- 3 特征值和特征向量的应用
- 4 矩阵的对角化
1 矩阵的特征值和特征向量究竟是什么?
矩阵实际上是一种变换,是一种旋转伸缩变换(方阵) 不是方阵的话还有可能是一种升维和降维的变换
直观理解可以看系列超赞视频线性代数-哔哩哔哩_Bilibili
比如A= ( 1 2 2 1 ) \begin{pmatrix}1&2\\2&1\end{pmatrix} (1221) x= ( 1 2 ) \begin{pmatrix}1\\2\end{pmatrix} (12)
我们给x左乘A实际上是对x进行了一次旋转伸缩变换 Ax= ( 5 4 ) \begin{pmatrix}5\\4\end{pmatrix} (54)
而我们如果仅仅是单纯的伸缩变换,而如果A对x仅仅只能伸缩变换,而不能旋转变换,则称为x为矩阵A的特征向量,伸缩变换的倍数即为特征值
2 求特征值和特征向量
(1)写出特征多项式 ∣ E − A ∣ = 0 |E-A|=0 ∣E−A∣=0 求得特征值
(2)代入特征值求解方程组,解即为我们的特征向量
矩阵的迹
矩阵乘积为行列式
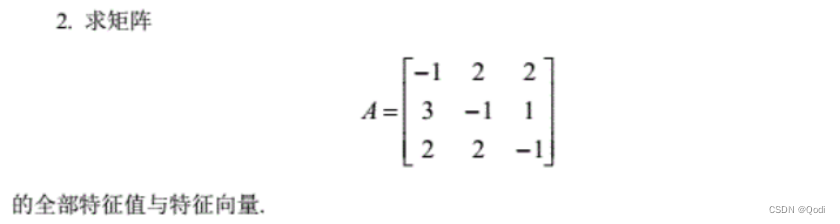

3 特征值和特征向量的应用
已知A的特征值
则 A − 1 A^{-1} A−1的特征值可求
A的一个多项式特征值可求
所以把我们要求的值转换为A的多项式,进而求出特征值,求出行列式的值
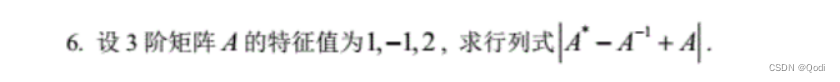
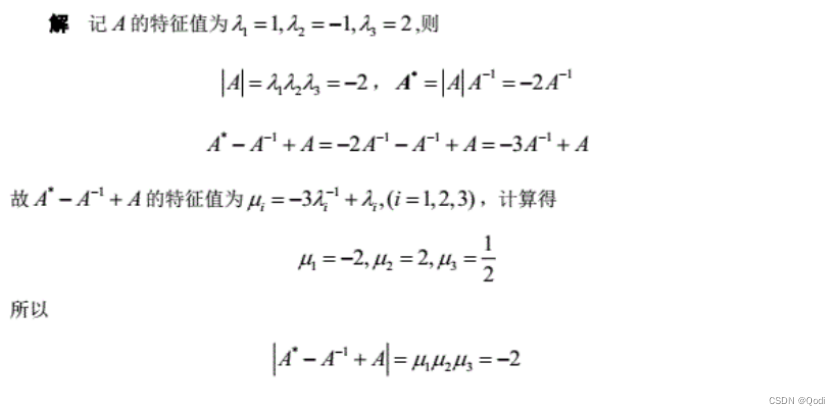
4 矩阵的对角化
非对称矩阵对角化
(1)求解特征值和特征向量
(2)特征向量组成我们的相乘矩阵P 特征值作为主对角线上的元素的对角矩阵就是我们对角化的矩阵
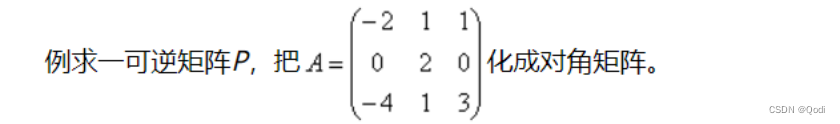

对称矩阵对角化求正交矩阵
(1)求解特征值值和特征向量
(2)施密特正交化重根对应的特征向量,再单位化所有特征向量
(3)取向量依次组成我们的正交矩阵Q
相关文章:

线性代数(五) | 矩阵对角化 特征值 特征向量
文章目录 1 矩阵的特征值和特征向量究竟是什么?2 求特征值和特征向量3 特征值和特征向量的应用4 矩阵的对角化 1 矩阵的特征值和特征向量究竟是什么? 矩阵实际上是一种变换,是一种旋转伸缩变换(方阵) 不是方阵的话还有可能是一种…...

读书笔记:彼得·德鲁克《认识管理》第12章 服务机构的绩效管理
一、章节内容概述 要提高服务机构和服务部门的绩效水平,需要的不是天才,相反,首先需要的是清晰的目标和任务,其次是把资源集中用于优先事项,再次需要明确的成果衡量标准,最后需要系统性地抛弃过时的目标和…...

基于FPGA的模板匹配红外目标跟踪算法设计
为什么要写这篇文章 我写这篇文章的原因是一天在B站看到了一个大神发的视频是关于跟踪一个无人机的,看到作者跟网友的回复说是用的图像匹配算法,我就在网上搜索相关资料,最终找到一篇文献。文献中对该算法的评价很高,满足制导系统…...
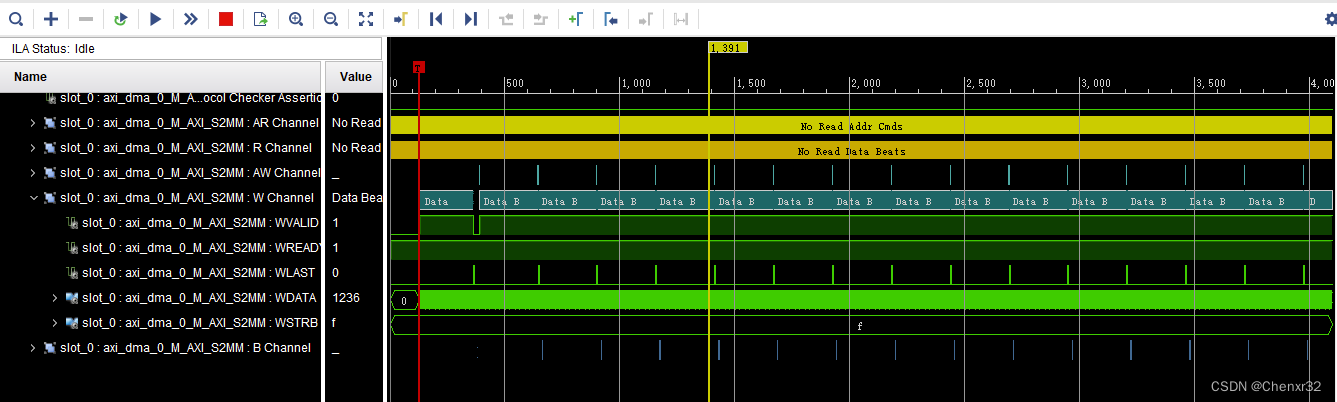
ZYNQ通过AXI DMA实现PL发送连续大量数据到PS DDR
硬件:ZYNQ7100 软件:Vivado 2017.4、Xilinx SDK 2017.4 ZYNQ PL 和 PS 的通信方式有 AXI GPIO、BRAM、DDR等。对于数据量较少、地址不连续、长度规则的情况,BROM 比较适用。而对于传输速度要求高、数据量大、地址连续的情况,比…...

用于强化学习的置换不变神经网络
一、介绍 如果强化学习代理提供的输入在训练中未明确定义,则通常表现不佳。一种新方法使 RL 代理能够正常运行,即使受到损坏、不完整或混乱的输入的影响也是如此。 “大脑能够使用来自皮肤的信息,就好像它来自眼睛一样。我们不是用眼睛看&…...

【华为OD题库-008】座位调整-Java
题目 疫情期间课堂的座位进行了特殊的调整,不能出现两个同学紧挨着,必须隔至少一个空位。给你一个整数数组desk表示当前座位的占座情况,由若干0和1组成,其中0表示没有占位,1表示占位。在不改变原有座位秩序情况下&…...

4 Paimon数据湖之Hive Catalog的使用
更多Paimon数据湖内容请关注:https://edu.51cto.com/course/35051.html Paimon提供了两种类型的Catalog:Filesystem Catalog和Hive Catalog。 Filesystem Catalog:会把元数据信息存储到文件系统里面。Hive Catalog:则会把元数据…...

Verilog刷题[hdlbits] :Bcdadd100
题目:Bcdadd100 You are provided with a BCD one-digit adder named bcd_fadd that adds two BCD digits and carry-in, and produces a sum and carry-out. 为您提供了一个名为bcd_fadd的BCD一位数加法器,它将两个BCD数字相加并带入,并生…...
Flink—— Data Source 介绍
Data Source 简介 Flink 做为一款流式计算框架,它可用来做批处理,即处理静态的数据集、历史的数据集;也可以用来做流处理,即实时的处理些实时数据流,实时的产生数据流结果,只要数据源源不断的过来ÿ…...
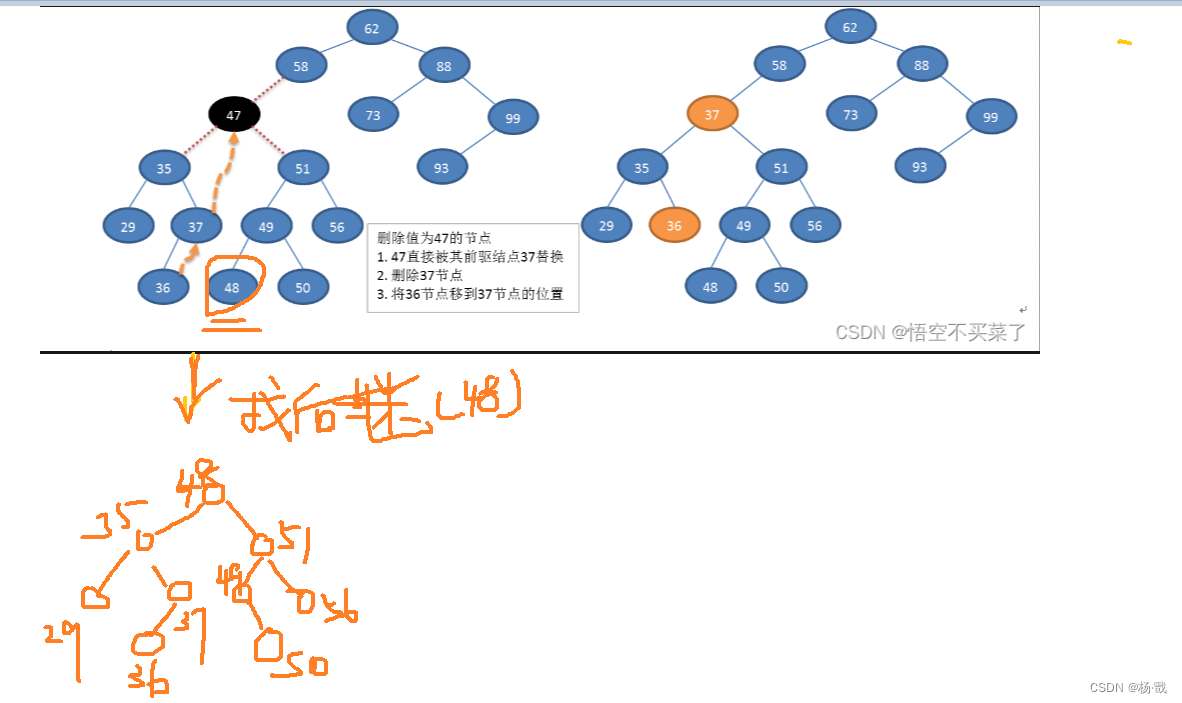
树之二叉排序树(二叉搜索树)
什么是排序树 说一下普通二叉树可不是左小右大的 插入的新节点是以叶子形式进行插入的 二叉排序树的中序遍历结果是一个升序的序列 下面是两个典型的二叉排序树 二叉排序树的操作 构造树的过程即是对无序序列进行排序的过程。 存储结构 通常采用二叉链表作为存储结构 不能 …...
管易云与电商平台的无代码集成:实现API连接与用户运营
管易云简介及其与电商平台的合作 金蝶管易云是金蝶集团旗下以电商为核心业务的子公司,是国内最早的电商ERP服务商之一,总部在上海,与淘宝、天猫、 京东、拼多多、抖音等300多家主流电商平台建立合作关系,同时管易云是互联网平台首…...
)
ElementUI的el-upload上传组件与表单一起提交遇到的各种问题以及解决办法(超详细,每个步骤都有详细解读)
背景: 使用ruoyi-vue进行2次开发,需要实现表单与文件上传一起提交,并且文件上传有4个,且文件校验很复杂,因此ruoyi-vue集成的上传组件FileUpload调试几天后发现真不太适用,最终选择element UI原生组件el-upload(FileUpload也是基于el-upload实现的),要实现表单与文件同…...

python flask_restful “message“: “Failed to decode JSON object: None“
1、问题表现 "message": "Failed to decode JSON object: None"2、出现的原因 Werkzeug 版本过高 3、解决方案 pip install Werkzeug2.0解决效果 可以正常显示json数据了 {"message": {"rate": "参数错误"} }...
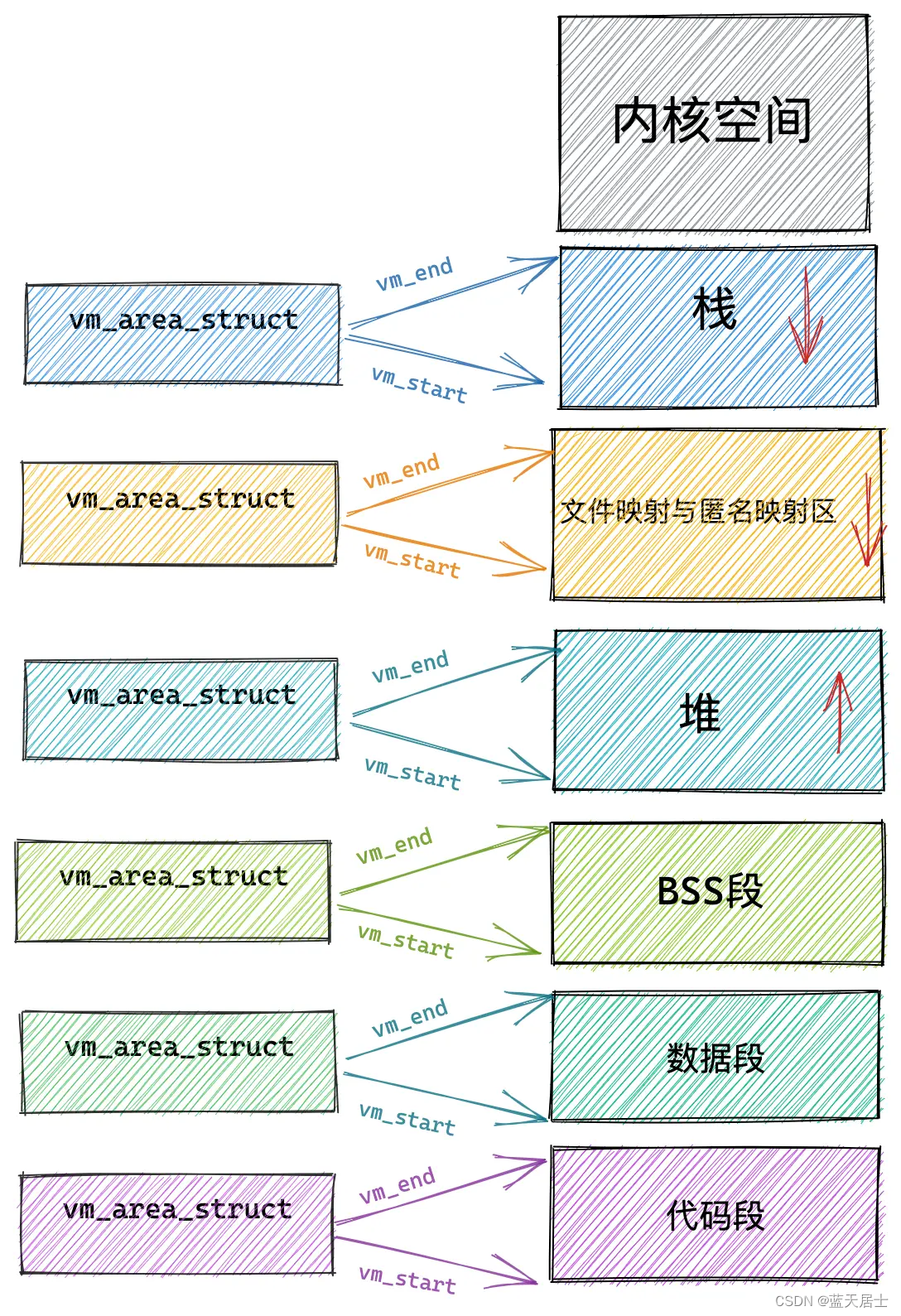
Linux内核有什么之内存管理子系统有什么第六回 —— 小内存分配(4)
接前一篇文章:Linux内核有什么之内存管理子系统有什么第五回 —— 小内存分配(3) 本文内容参考: linux进程虚拟地址空间 《趣谈Linux操作系统 核心原理篇:第四部分 内存管理—— 刘超》 特此致谢! 二、小…...
)
【OpenHarmony内核】Harmony内核之线程操作函数(二)
文章目录 前言一、获取线程优先级二、转交控制运行权三、挂起线程3.1 线程的挂起是什么意思?3.2 函数介绍四、恢复线程五、分离指定的线程5.1 分离线程是什么意思5.2 函数介绍六、等待线程终止运行七、终止当前线程的运行八、终止指定线程的运行九、获取活跃线程数总结前言 O…...

二十五、W5100S/W5500+RP2040树莓派Pico<Modebus TCP Server示例>
文章目录 1 前言2 简介2 .1 什么是Modbus TCP?2.2 Modbus TCP指令介绍2.3 请求数据过程2.4 Modbus TCP协议优点2.5 Modbus TCP应用场景 3 WIZnet以太网芯片4 Modbus TCP示例概述以及使用4.1 流程图4.2 准备工作核心4.3 连接方式4.4 主要代码概述4.5 结果演示 5 注意…...

Android画个圆点状态灯
1、创建一个 XML 文件在 res/drawable 目录下(默认为黑色) <?xml version"1.0" encoding"utf-8"?> <shape xmlns:android"http://schemas.android.com/apk/res/android"android:shape"oval"><…...

高性能网络编程 - 解读3种线程模型
文章目录 Pre线程模型1:传统阻塞 I/O 服务模型线程模型2:Reactor 模式Reactor 模式的基本设计思想Reactor 模式中的关键组成3种典型实现单 Reactor 单线程单 Reactor 多线程主从 Reactor 多线程 小结 线程模型3:Proactor 模型 Pre 高性能网络…...
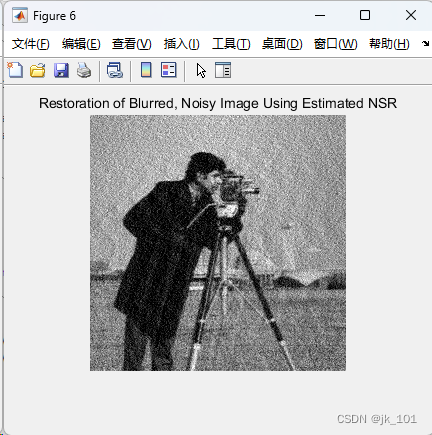
MATLAB中deconvwnr函数用法
目录 语法 说明 示例 使用 Wiener 滤波对图像进行去模糊处理 deconvwnr函数的功能是使用 Wiener 滤波对图像进行去模糊处理。 语法 J deconvwnr(I,psf,nsr) J deconvwnr(I,psf,ncorr,icorr) J deconvwnr(I,psf) 说明 J deconvwnr(I,psf,nsr) 使用 Wiener 滤波算法对…...

赛宁网安入选国家工业信息安全漏洞库(CICSVD)2023年度技术组成员单
近日,由国家工业信息安全发展研究中心、工业信息安全产业发展联盟主办的“2023工业信息安全大会”在北京成功举行。 会上,国家工业信息安全发展研究中心对为国家工业信息安全漏洞库(CICSVD)提供技术支持的单位授牌表彰。北京赛宁…...

RestClient
什么是RestClient RestClient 是 Elasticsearch 官方提供的 Java 低级 REST 客户端,它允许HTTP与Elasticsearch 集群通信,而无需处理 JSON 序列化/反序列化等底层细节。它是 Elasticsearch Java API 客户端的基础。 RestClient 主要特点 轻量级ÿ…...

(LeetCode 每日一题) 3442. 奇偶频次间的最大差值 I (哈希、字符串)
题目:3442. 奇偶频次间的最大差值 I 思路 :哈希,时间复杂度0(n)。 用哈希表来记录每个字符串中字符的分布情况,哈希表这里用数组即可实现。 C版本: class Solution { public:int maxDifference(string s) {int a[26]…...

地震勘探——干扰波识别、井中地震时距曲线特点
目录 干扰波识别反射波地震勘探的干扰波 井中地震时距曲线特点 干扰波识别 有效波:可以用来解决所提出的地质任务的波;干扰波:所有妨碍辨认、追踪有效波的其他波。 地震勘探中,有效波和干扰波是相对的。例如,在反射波…...

React hook之useRef
React useRef 详解 useRef 是 React 提供的一个 Hook,用于在函数组件中创建可变的引用对象。它在 React 开发中有多种重要用途,下面我将全面详细地介绍它的特性和用法。 基本概念 1. 创建 ref const refContainer useRef(initialValue);initialValu…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...
)
IGP(Interior Gateway Protocol,内部网关协议)
IGP(Interior Gateway Protocol,内部网关协议) 是一种用于在一个自治系统(AS)内部传递路由信息的路由协议,主要用于在一个组织或机构的内部网络中决定数据包的最佳路径。与用于自治系统之间通信的 EGP&…...

visual studio 2022更改主题为深色
visual studio 2022更改主题为深色 点击visual studio 上方的 工具-> 选项 在选项窗口中,选择 环境 -> 常规 ,将其中的颜色主题改成深色 点击确定,更改完成...

【第二十一章 SDIO接口(SDIO)】
第二十一章 SDIO接口 目录 第二十一章 SDIO接口(SDIO) 1 SDIO 主要功能 2 SDIO 总线拓扑 3 SDIO 功能描述 3.1 SDIO 适配器 3.2 SDIOAHB 接口 4 卡功能描述 4.1 卡识别模式 4.2 卡复位 4.3 操作电压范围确认 4.4 卡识别过程 4.5 写数据块 4.6 读数据块 4.7 数据流…...

鸿蒙中用HarmonyOS SDK应用服务 HarmonyOS5开发一个医院查看报告小程序
一、开发环境准备 工具安装: 下载安装DevEco Studio 4.0(支持HarmonyOS 5)配置HarmonyOS SDK 5.0确保Node.js版本≥14 项目初始化: ohpm init harmony/hospital-report-app 二、核心功能模块实现 1. 报告列表…...
