高通SDX12:ASoC 音频框架浅析
一、简介
ASoC–ALSA System on Chip ,是建立在标准ALSA驱动层上,为了更好地支持嵌入式处理器和移动设备中的音频Codec的一套软件体系。
本文基于高通SDX12平台,对ASoC框架做一个分析。
二、整体框架
1. 硬件层面
嵌入式Linux设备的Audio subsystem可以划分为Machine(板载硬件)、Codec、Platform(SoC)三个部分,三者的的关系大致如下图所示:
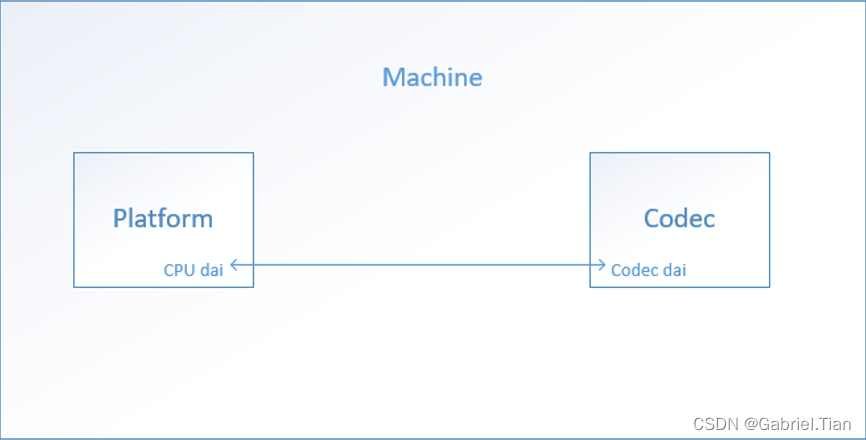
2. 软件层面
对应于ASoC的硬件框架,其软件也分为三个部分,具体内容如下:
2.1 Codec驱动
遵循ASoC设计原则,Codec需要和Platform无关(解耦),它本身包含了一些音频控件(controls)、音频接口、DAPM(动态音频电源管理)以及Codec本身的IO功能
2.2 Platform驱动
在ASoC中,platform部分的驱动代码一般位于sound/soc/soc-core.c文件中,这个文件是ASoC框架的核心实现,包括platform驱动的注册、初始化和管理等功能。
2.3
相关文章:

高通SDX12:ASoC 音频框架浅析
一、简介 ASoC–ALSA System on Chip ,是建立在标准ALSA驱动层上,为了更好地支持嵌入式处理器和移动设备中的音频Codec的一套软件体系。 本文基于高通SDX12平台,对ASoC框架做一个分析。 二、整体框架 1. 硬件层面 嵌入式Linux设备的Audio subsystem可以划分为Machine(板…...

国际化:i18n
什么是国际化? 国际化也称作i18n,其来源是英文单词 internationalization的首末字符和n,18为中间的字符数。由于软件发行可能面向多个国家,对于不同国家的用户,软件显示不同语言的过程就是国际化。通常来讲࿰…...
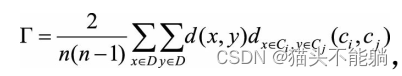
【机器学习5】无监督学习聚类
相比于监督学习, 非监督学习的输入数据没有标签信息, 需要通过算法模型来挖掘数据内在的结构和模式。 非监督学习主要包含两大类学习方法: 数据聚类和特征变量关联。 1 K均值聚类及优化及改进模型 1.1 K-means 聚类是在事先并不知道任何样…...

风景照片不够清晰锐利,四招帮你轻松解决
我们大家在拍摄风景照的时候都希望能够拍摄出清晰锐利的照片。可能会有人问:“什么是锐利?”我们可以从锐度来给大家简单解说下。锐度是反映图片平面清晰度和图像边缘对比度的一个参数。锐度较高的画面,微小的细节部分也会表现得很清晰&#…...

List中的迭代器实现【C++】
List中的迭代器实现【C】 一. list的结构二. 迭代器的区别三. 迭代器的实现i. 类的设计ii. 重载iii. !重载iiii. begin()iiiii. end()iiiii. operator* 四.测试五. const迭代器的实现i. 实现ii 优化实现 六. 整体代码 一. list的结构 其实按照习惯来说,应该要专门出…...
VB.NET三层之用户查询窗体
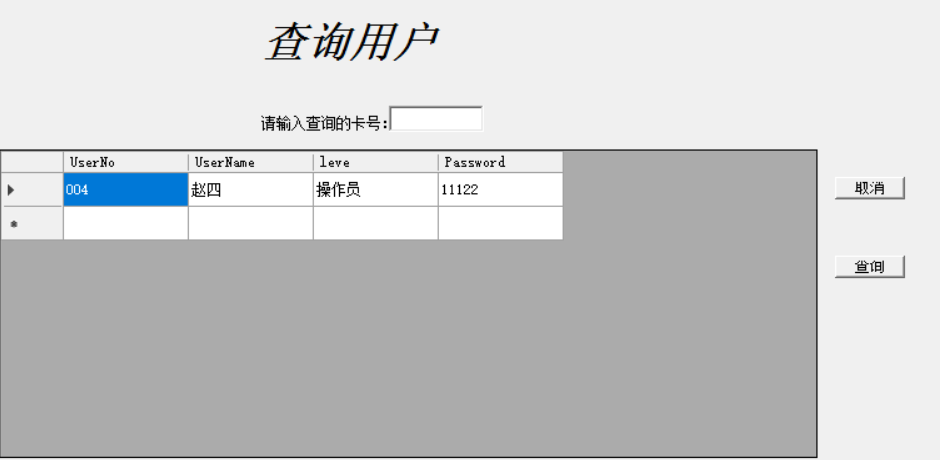
目录 前言: 过程: UI层代码展示: BLL层代码展示: DAL层代码展示: 查询用户效果图: 总结: 前言: 想要对用户进行查询,需要用到控件DataGrideView,通过代码的形式将数据库表中的数据显示在DataGrideview控件中,不用对DatGridView控件…...
Django之路由层
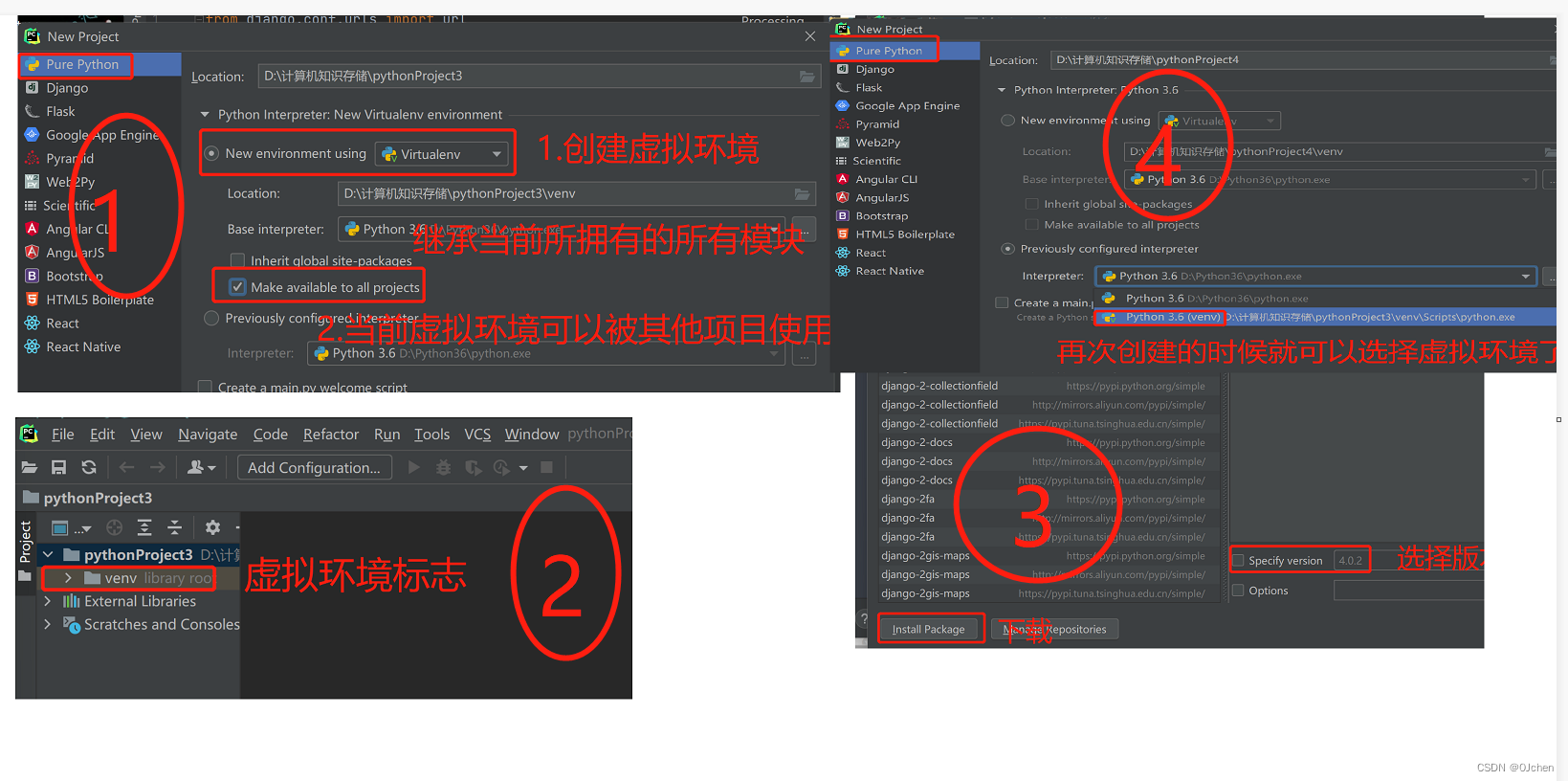
文章目录 路由匹配语法路由配置注意事项转换器注册自定义转化器 无名分组和有名分组无名分组有名分组 反向解析简介普通反向解析无名分组、有名分组之反向解析 路由分发简介为什么要用路由分发?路由分发实现 伪静态的概念名称空间虚拟环境什么是虚拟环境?…...
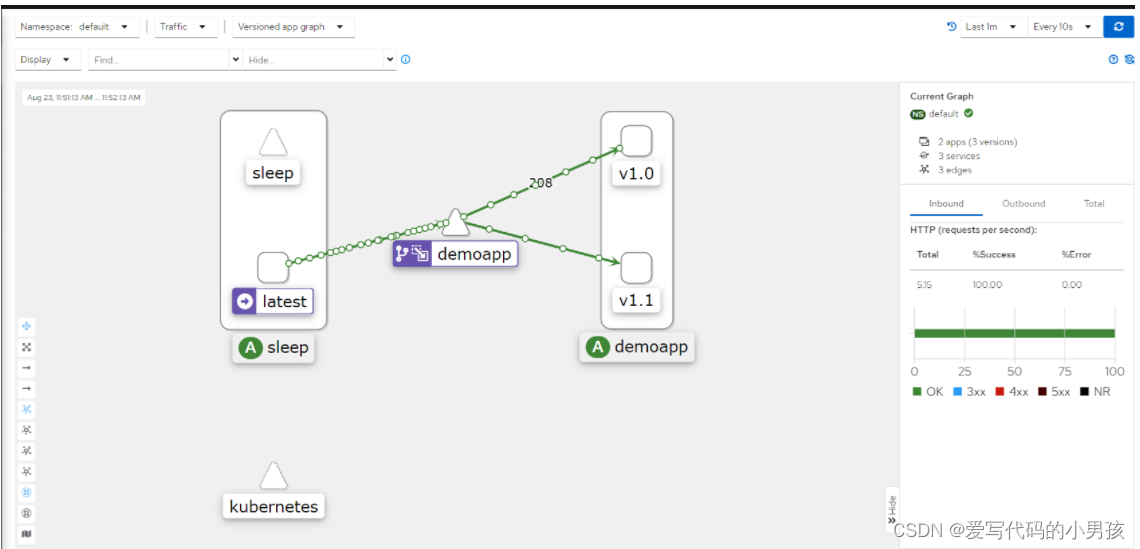
【06】VirtualService高级流量功能
5.3 weight 部署demoapp v10和v11版本 --- apiVersion: apps/v1 kind: Deployment metadata:labels:app: demoappv10version: v1.0name: demoappv10 spec:progressDeadlineSeconds: 600replicas: 3selector:matchLabels:app: demoappversion: v1.0template:metadata:labels:app…...

322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。 示…...
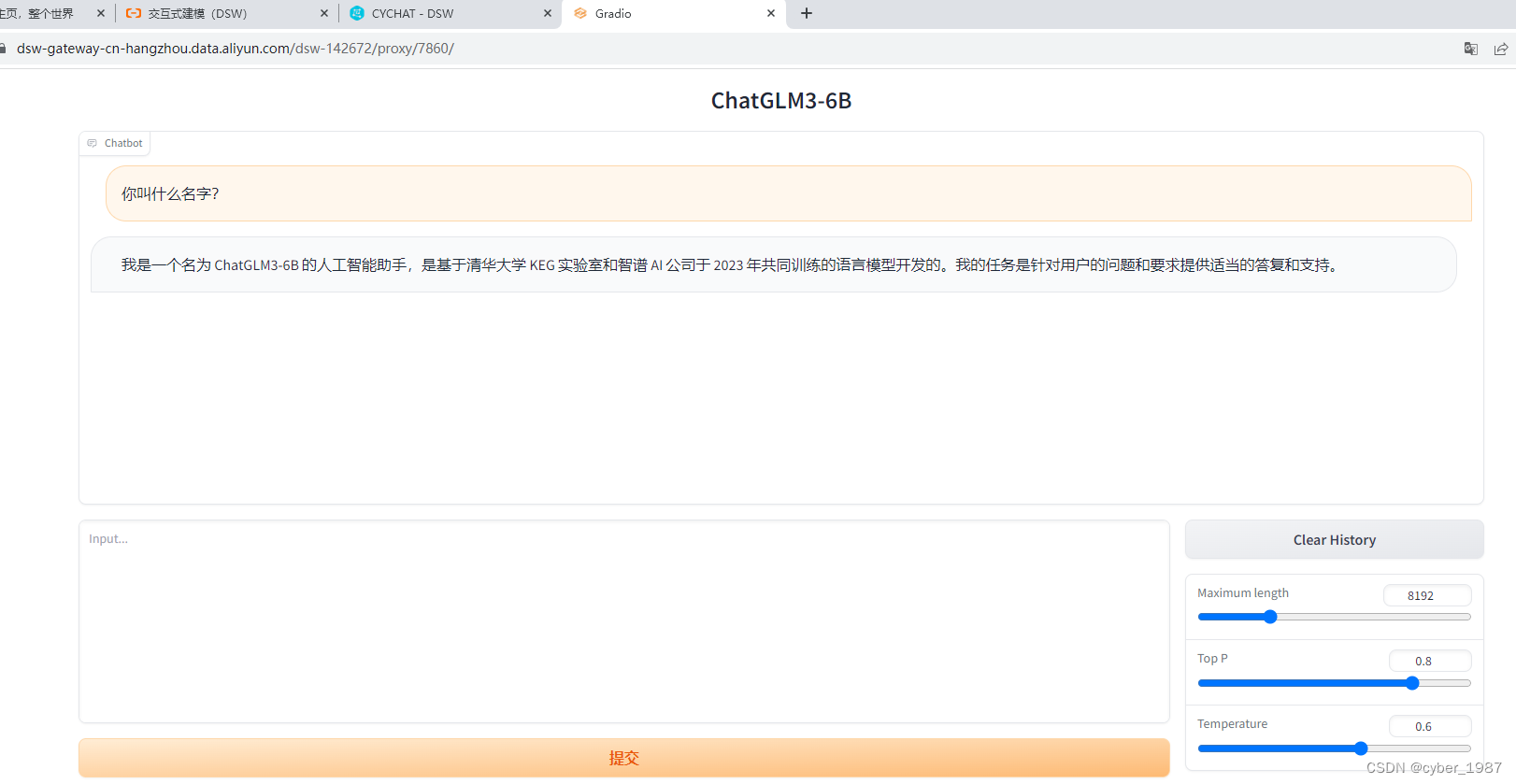
【大模型-第一篇】在阿里云上部署ChatGLM3
前言 好久没写博客了,最近大模型盛行,尤其是ChatGLM3上线,所以想部署试验一下。 本篇只是第一篇,仅仅只是部署而已,没有FINETUNE、没有Langchain更没有外挂知识库,所以从申请资源——>开通虚机——>…...

2023-11-14 mysql-主从复制-相关文档
摘要: 2023-11-14 mysql-主从复制-相关文档 官方文档: MySQL :: MySQL 8.0 Reference Manual :: 17 Replication MySQL :: MySQL 8.0 Reference Manual :: 18 Group Replication 相关参数: mysql> show variables like %repl%; +-----------------------------------------…...
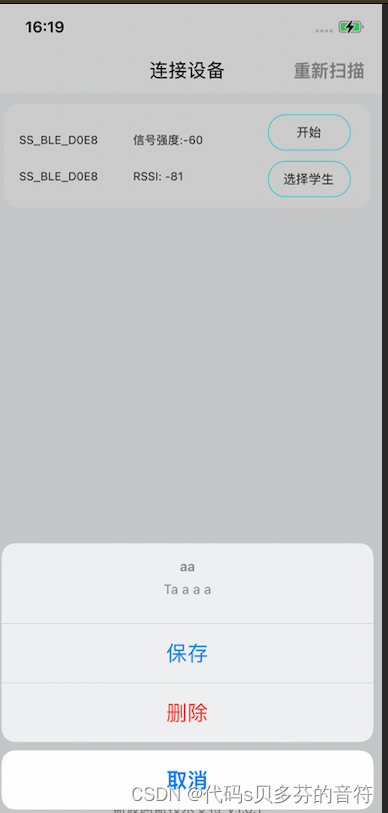
ios 对话框 弹框,输入对话框 普通对话框
1 普通对话框 UIAlertController* alert [UIAlertController alertControllerWithTitle:"a" message:"alert12222fdsfs" pr…...
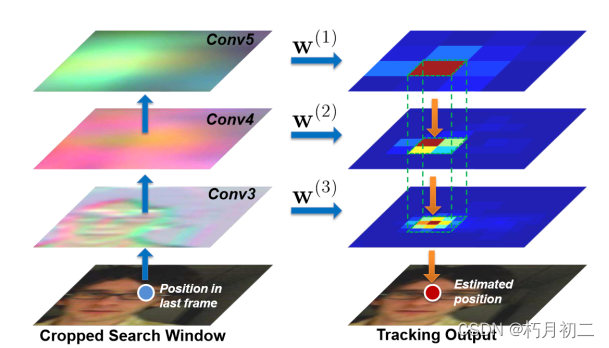
(论文阅读23/100)Hierarchical Convolutional Features for Visual Tracking
文献阅读笔记(分层卷积特征) 简介 题目 Hierarchical Convolutional Features for Visual Tracking 作者 Chao Ma, Jia-Bin Huang, Xiaokang Yang and Ming-Hsuan Yang 原文链接 arxiv.org/pdf/1707.03816.pdf 关键词 Hierarchical convolution…...

基于IGT-DSER智能网关实现GE的PAC/PLC与罗克韦尔(AB)的PLC之间通讯
工业自动化领域的IGT-DSER智能网关模块支持GE、西门子、三菱、欧姆龙、AB等各种品牌的PLC之间通讯(相关资料下载),同时也支持PLC与Modbus协议的工业机器人、智能仪表等设备通讯。网关有多个网口、串口,也可选择WIFI无线通讯。无需编程开发,只…...

创建符合 Web 可访问性标准的 HTML 布局
人们常说网络可访问性是当今万维网的“必须”。“Web 可访问性”一词定义了开发人员需要遵循的一组准则,以使残障人士和 Web 应用程序的交互更加方便。任何网站的内容、UI/UX 设计和布局都应该易于访问。在本文中,Logicify团队为 HTML/CSS 开发人员提供了…...
SQL学习(CTFhub)整数型注入,字符型注入,报错注入 -----手工注入+ sqlmap注入
目录 整数型注入 手工注入 为什么要将1设置为-1呢? sqlmap注入 sqlmap注入步骤: 字符型注入 手工注入 sqlmap注入 报错注入 手工注入 sqlmap注入 整数型注入 手工注入 先输入1 接着尝试2,3,2有回显,而3没有回显…...

数字人部署之VITS+Wav2lip数据流转处理以提高实时性
一、模型 VITS模型训练教程VITS-从零开始微调(finetune)训练并部署指南-支持本地云端 Wav2lip是2D数字人,可参考训练嘴型同步模型Wav2Lip PS:以上模型都是开源可用。 二. VITS数据处理问题 VITS模型的输出为一维的numpy类型数据ÿ…...

GPT 学习法:复杂文献轻松的完美理解、在庞大的不确性中找到确定性
GPT 学习法:复杂文献轻松的完美理解、在庞大的不确性中找到确定性 复杂文献 - 基础理解GPT 理解法 - 举例子、归纳、逻辑链推导本质、图示、概念放大器GPT 分析法 - 二分、矩阵、公式、要素、过程 做复杂题:在庞大的不确性中找到确定性思维追踪ÿ…...

前端简单的爱心形状
首先需要创建一个 HTML 文件,然后在其中添加 CSS 样式和 JavaScript 代码。以下是一个简单的示例: 创建一个名为 loveheart.html 的文件 <!DOCTYPE html> <html lang"zh"> <head><meta charset"UTF-8"><…...
)
acwing算法基础之数学知识--求数a的欧拉函数值phi(a)
目录 1 基础知识2 模板3 工程化 1 基础知识 数a的欧拉函数 ϕ ( a ) \phi(a) ϕ(a):表示1~n中与n互质的数的个数。其中两个数互质,是指这两个数的最大公约数为1。 根据定义,我们可以写出如下方法, int gcd(int a, int b) {retu…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

树莓派超全系列教程文档--(61)树莓派摄像头高级使用方法
树莓派摄像头高级使用方法 配置通过调谐文件来调整相机行为 使用多个摄像头安装 libcam 和 rpicam-apps依赖关系开发包 文章来源: http://raspberry.dns8844.cn/documentation 原文网址 配置 大多数用例自动工作,无需更改相机配置。但是,一…...

Opencv中的addweighted函数
一.addweighted函数作用 addweighted()是OpenCV库中用于图像处理的函数,主要功能是将两个输入图像(尺寸和类型相同)按照指定的权重进行加权叠加(图像融合),并添加一个标量值&#x…...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
免费数学几何作图web平台
光锐软件免费数学工具,maths,数学制图,数学作图,几何作图,几何,AR开发,AR教育,增强现实,软件公司,XR,MR,VR,虚拟仿真,虚拟现实,混合现实,教育科技产品,职业模拟培训,高保真VR场景,结构互动课件,元宇宙http://xaglare.c…...

Git 3天2K星标:Datawhale 的 Happy-LLM 项目介绍(附教程)
引言 在人工智能飞速发展的今天,大语言模型(Large Language Models, LLMs)已成为技术领域的焦点。从智能写作到代码生成,LLM 的应用场景不断扩展,深刻改变了我们的工作和生活方式。然而,理解这些模型的内部…...

从 GreenPlum 到镜舟数据库:杭银消费金融湖仓一体转型实践
作者:吴岐诗,杭银消费金融大数据应用开发工程师 本文整理自杭银消费金融大数据应用开发工程师在StarRocks Summit Asia 2024的分享 引言:融合数据湖与数仓的创新之路 在数字金融时代,数据已成为金融机构的核心竞争力。杭银消费金…...

Web后端基础(基础知识)
BS架构:Browser/Server,浏览器/服务器架构模式。客户端只需要浏览器,应用程序的逻辑和数据都存储在服务端。 优点:维护方便缺点:体验一般 CS架构:Client/Server,客户端/服务器架构模式。需要单独…...

前端中slice和splic的区别
1. slice slice 用于从数组中提取一部分元素,返回一个新的数组。 特点: 不修改原数组:slice 不会改变原数组,而是返回一个新的数组。提取数组的部分:slice 会根据指定的开始索引和结束索引提取数组的一部分。不包含…...
