堆的应用-----Top k 问题
目录
前言
Topk问题
1.问题描述
2.解决方法
3.代码实现(C/C++)
前言
在人工智能算法岗位的面试中,TopK是问得最多的几个问题之一:
到底有几种方法?
这些方案里蕴含的优化思路究竟是怎么样的?
为啥TopK这么受欢迎呢?究其原因,还是因为它不仅在AI领域广泛应用,比如max pooling,mAP计算等;还涵盖了算法专业的很多必备知识,比如快速排序,二分查找,分治减治,大小顶堆等;一些适当的变换,还可以考察应聘者的思维灵活度。
下面的文章转自架构师之路,是笔者见过此类文章中总结的最透彻的一篇,为了行文流畅,文章有增删。
前段时间我们学习过了数据结构堆以及堆排序算法,堆是一种完全二叉树,那今天我们学习堆的应用,解决topk问题,下面就一起来看看吧。
(相关链接:数据结构-----堆(完全二叉树)-CSDN博客)
Topk问题
1.问题描述
从arr[1, n]这n个数中,找出最大的k个数,这就是经典的TopK问题。
看上去是不是非常直白明了呢?那确实是,但是怎么去解决这个问题?当然我们会想到排序去处理,把这个数组进行排序,然后直接就可以找到了。但是排序的话会把一些不必要的数进行排序处理,也就是说时间复杂度会比较大,但是如果我们单单对前k个大的数字进行单独处理,那效果是不是更好呢?下面我们就看一看堆是怎么实现的。
2.解决方法
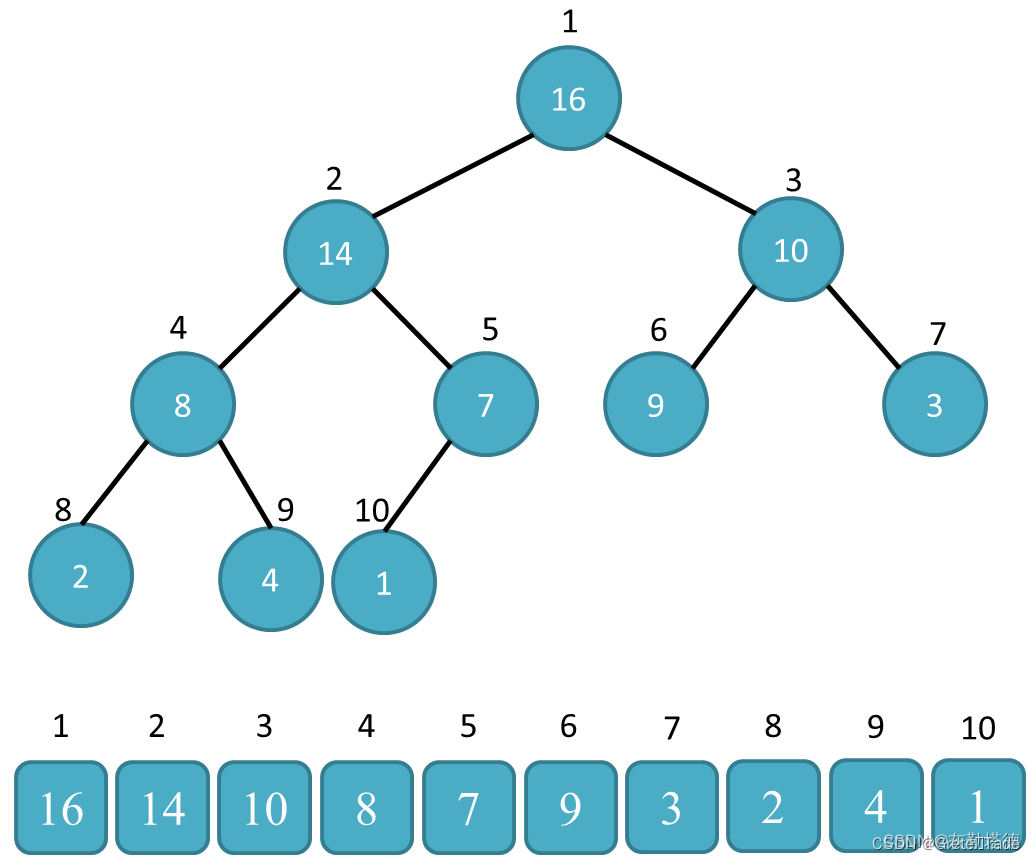
我们获取到当前的数组的时候,然后就创建一个大堆,如图所示,其特点就是上面的元素比下面的元素要大。创建好大堆之后,我们就可以进行后继处理。当前大堆最大的元素就是在第一个位置,我们把第一个位置(最大元素),与最后一个位置的元素进行位置交换,然后把最后一个位置的元素踢出当前的堆,在前面n-1个元素里面再找最大值即可,依次重复以上的操作,执行k次就完成了问题的解决。
3.代码实现(C/C++)
#include<stdio.h>
#include<stdlib.h>//交换数字
void swap(int* a, int* b) {int t = *a;*a = *b;*b = t;
}//向下调整
void adjust_down(int* arr, int par, int n) {int child = par * 2 + 1;while (child < n) {if (arr[child] < arr[child + 1] && child + 1 < n)child++;if (arr[par] < arr[child]) {swap(&arr[par], &arr[child]);par = child;child = par * 2 + 1;}elsebreak;}
}//函数接口
void Top_k(int* arr, int n,int k) {//先创建这个堆for (int i = (n - 1) / 2; i >= 0; i--) {adjust_down(arr, i, n);}//然后就是获取当前堆中的最大值int end = n - 1;int count = 0;while (count < k) {//当前最大值下标为0,把最大值的数与最后一个数进行交换swap(&arr[end], &arr[0]);//end--,把最大值踢出当前堆,然后从剩下的n-1个数字的堆继续找最大值adjust_down(arr, 0, end);end--;count++;}printf("前%d大的数是:\n", k);for (int i = n - 1; i > n - 1 - count; i--) {printf("%d ", arr[i]);}
}int main() {int arr[] = { 5,1,4,7,8,9,3,4,5,6,7,10,55 };int k = 3;Top_k(arr, sizeof(arr) / sizeof(int), k);
}以上就是本期的全部内容了,我们下次见!
分享一张壁纸:
相关文章:

堆的应用-----Top k 问题
目录 前言 Topk问题 1.问题描述 2.解决方法 3.代码实现(C/C) 前言 在人工智能算法岗位的面试中,TopK是问得最多的几个问题之一: 到底有几种方法? 这些方案里蕴含的优化思路究竟是怎么样的? 为啥T…...

11月14日星期二今日早报简报微语报早读
11月14日星期二,农历十月初二,早报微语早读。 1、江西南城县:限时发放购房补贴政策,三孩家庭每平方米最高补贴500元; 2、2023年中国内地电影市场累计票房突破500亿元; 3、市场监管总局:在全国…...
Spark读取excel文件
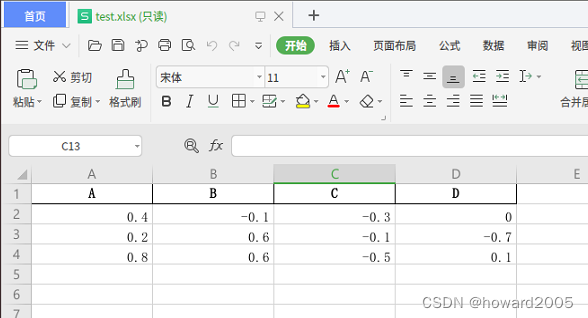
文章目录 一、excel数据源转成csv二、Spark读取csv文件(一)启动spark-shell(二)读取csv生成df(三)查看df内容一、excel数据源转成csv 集群bigdata - ubuntu: 192.168.191.19master(bigdata1) - centos: 192.168.23.78 slave1(bigdata2) - centos: 192.168.23.79 slave2(b…...
LLM大语言模型(典型ChatGPT)入门指南
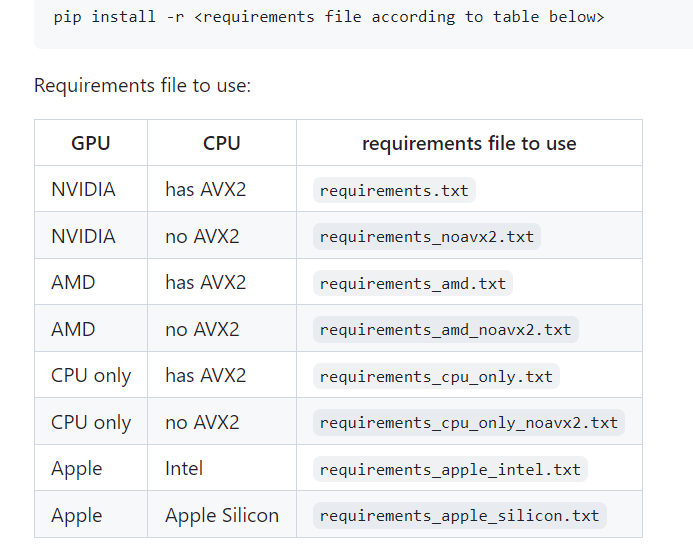
文章目录 一、基础概念学习篇1.1 langchain视频学习笔记1.2 Finetune LLM视频学习笔记 二、实践篇2.1 预先下载模型:2.2 LangChain2.3 Colab demo2.3 text-generation-webui 三、国内项目实践langchain-chatchat 一、基础概念学习篇 1.1 langchain视频学习笔记 lan…...
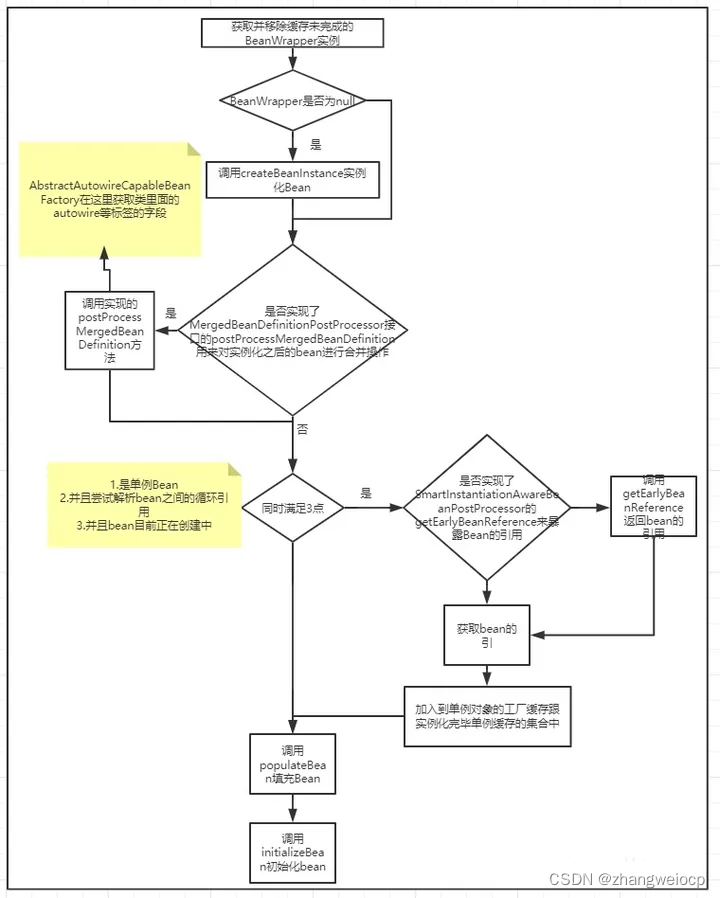
Spring IOC - Bean的生命周期之实例化
在Spring启动流程文章中讲到,容器的初始化是从refresh方法开始的,其在初始化的过程中会调用finishBeanFactoryInitialization方法。 而在该方法中则会调用DefaultListableBeanFactory#preInstantiateSingletons方法,该方法的核心作用是初始化…...

前端 BUG 总结
文章目录 CSS 样式1、Chrome 89 版本期不再支持 /deep/,请勿使用嵌套 /deep/2、圆角按钮 button 点击后出现矩形框线3、怪异模式4、border 1 像素在手机上显示问题5、文本溢出问题 JavaScript 脚本1、移动端点击穿透2、使用parseInt时必须补全第二个参数 radix3、有…...
【蓝桥杯软件赛 零基础备赛20周】第3周——填空题
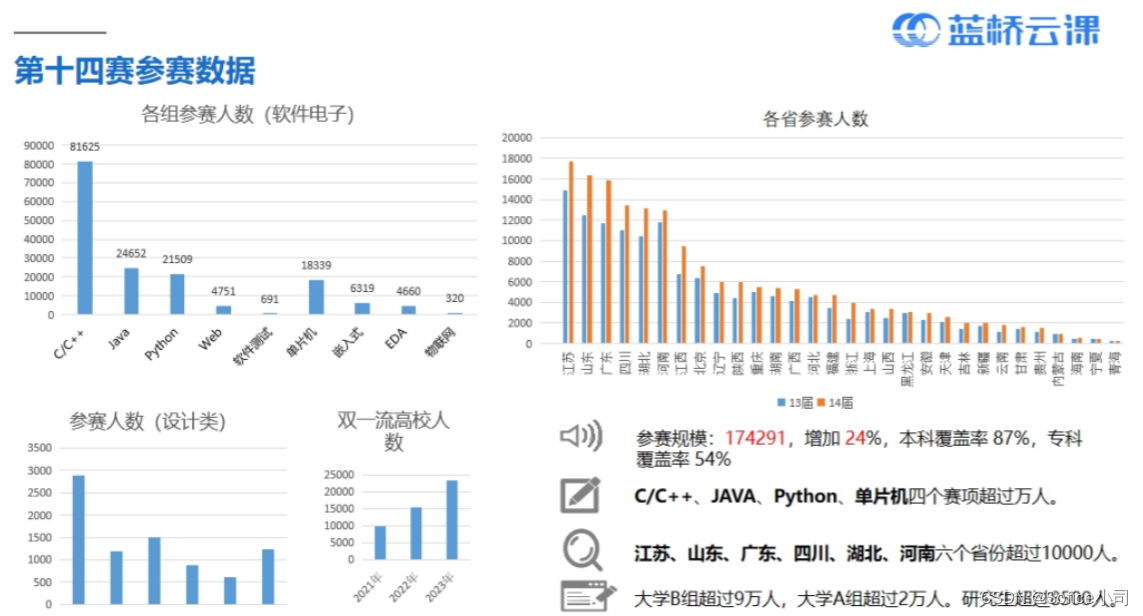
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集 20周的完整安排请点击:20周计划 文章目录 00. 2023年第14届参赛数据0. 上一周答疑1. 填空…...
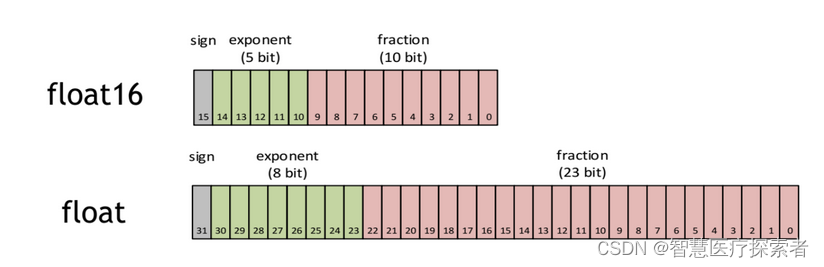
Pytorch自动混合精度的计算:torch.cuda.amp.autocast
1 autocast介绍 1.1 什么是AMP? 默认情况下,大多数深度学习框架都采用32位浮点算法进行训练。2017年,NVIDIA研究了一种用于混合精度训练的方法,该方法在训练网络时将单精度(FP32)与半精度(FP16)结合在一起ÿ…...
一文看懂香港优才计划和高才通计划的区别和优势?如何选?
一文看懂香港优才计划和高才通计划的区别和优势?如何选? 为什么很多人都渴望有个香港身份? 英文这里和内地文化相近,语言相通,同时税率较低、没有外汇管制,有稳定金融体制和良好的营商环境,诸多…...

DTC Network旗下代币DSTC大蒜头即将上线,市场热度飙升
全球数字资产领导者DTC Network宣布其代币DSTC(大蒜头)即将于近期上线,引发市场广泛关注。DTC Network以其创新性的区块链技术和多维度的网络构建,致力于打造一个融合Web3.0、元宇宙和DAPP应用的去中心化聚合公共平台,…...
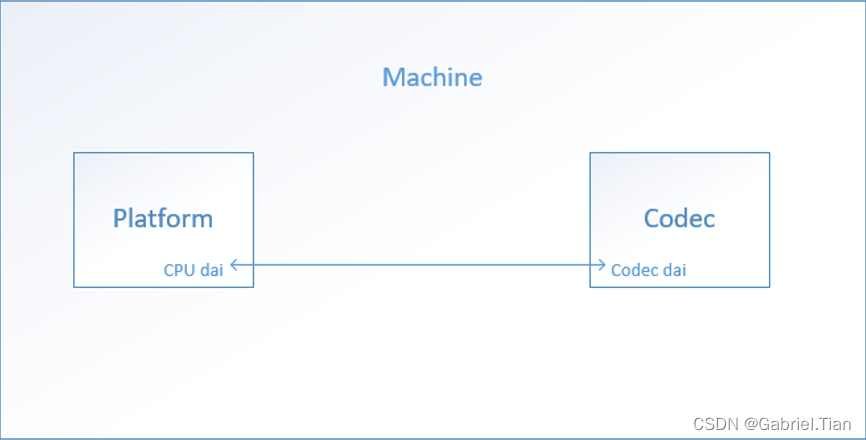
高通SDX12:ASoC 音频框架浅析
一、简介 ASoC–ALSA System on Chip ,是建立在标准ALSA驱动层上,为了更好地支持嵌入式处理器和移动设备中的音频Codec的一套软件体系。 本文基于高通SDX12平台,对ASoC框架做一个分析。 二、整体框架 1. 硬件层面 嵌入式Linux设备的Audio subsystem可以划分为Machine(板…...

国际化:i18n
什么是国际化? 国际化也称作i18n,其来源是英文单词 internationalization的首末字符和n,18为中间的字符数。由于软件发行可能面向多个国家,对于不同国家的用户,软件显示不同语言的过程就是国际化。通常来讲࿰…...
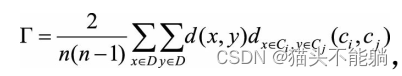
【机器学习5】无监督学习聚类
相比于监督学习, 非监督学习的输入数据没有标签信息, 需要通过算法模型来挖掘数据内在的结构和模式。 非监督学习主要包含两大类学习方法: 数据聚类和特征变量关联。 1 K均值聚类及优化及改进模型 1.1 K-means 聚类是在事先并不知道任何样…...

风景照片不够清晰锐利,四招帮你轻松解决
我们大家在拍摄风景照的时候都希望能够拍摄出清晰锐利的照片。可能会有人问:“什么是锐利?”我们可以从锐度来给大家简单解说下。锐度是反映图片平面清晰度和图像边缘对比度的一个参数。锐度较高的画面,微小的细节部分也会表现得很清晰&#…...

List中的迭代器实现【C++】
List中的迭代器实现【C】 一. list的结构二. 迭代器的区别三. 迭代器的实现i. 类的设计ii. 重载iii. !重载iiii. begin()iiiii. end()iiiii. operator* 四.测试五. const迭代器的实现i. 实现ii 优化实现 六. 整体代码 一. list的结构 其实按照习惯来说,应该要专门出…...
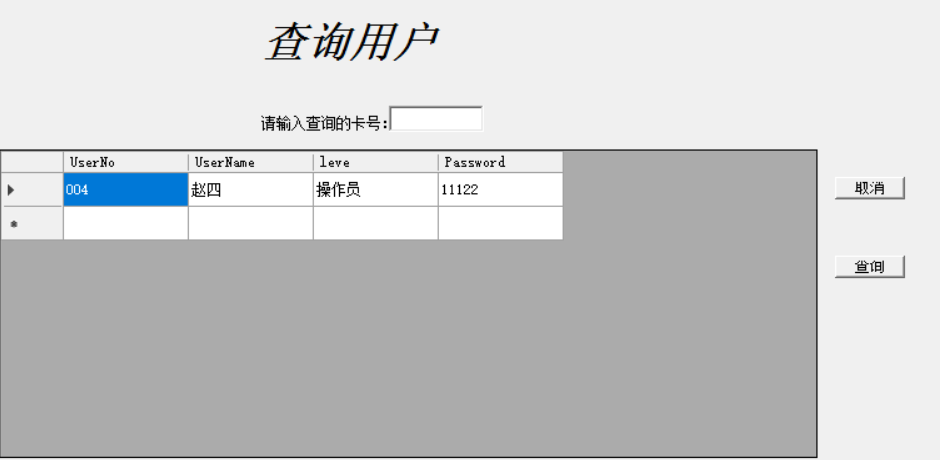
VB.NET三层之用户查询窗体
目录 前言: 过程: UI层代码展示: BLL层代码展示: DAL层代码展示: 查询用户效果图: 总结: 前言: 想要对用户进行查询,需要用到控件DataGrideView,通过代码的形式将数据库表中的数据显示在DataGrideview控件中,不用对DatGridView控件…...
Django之路由层
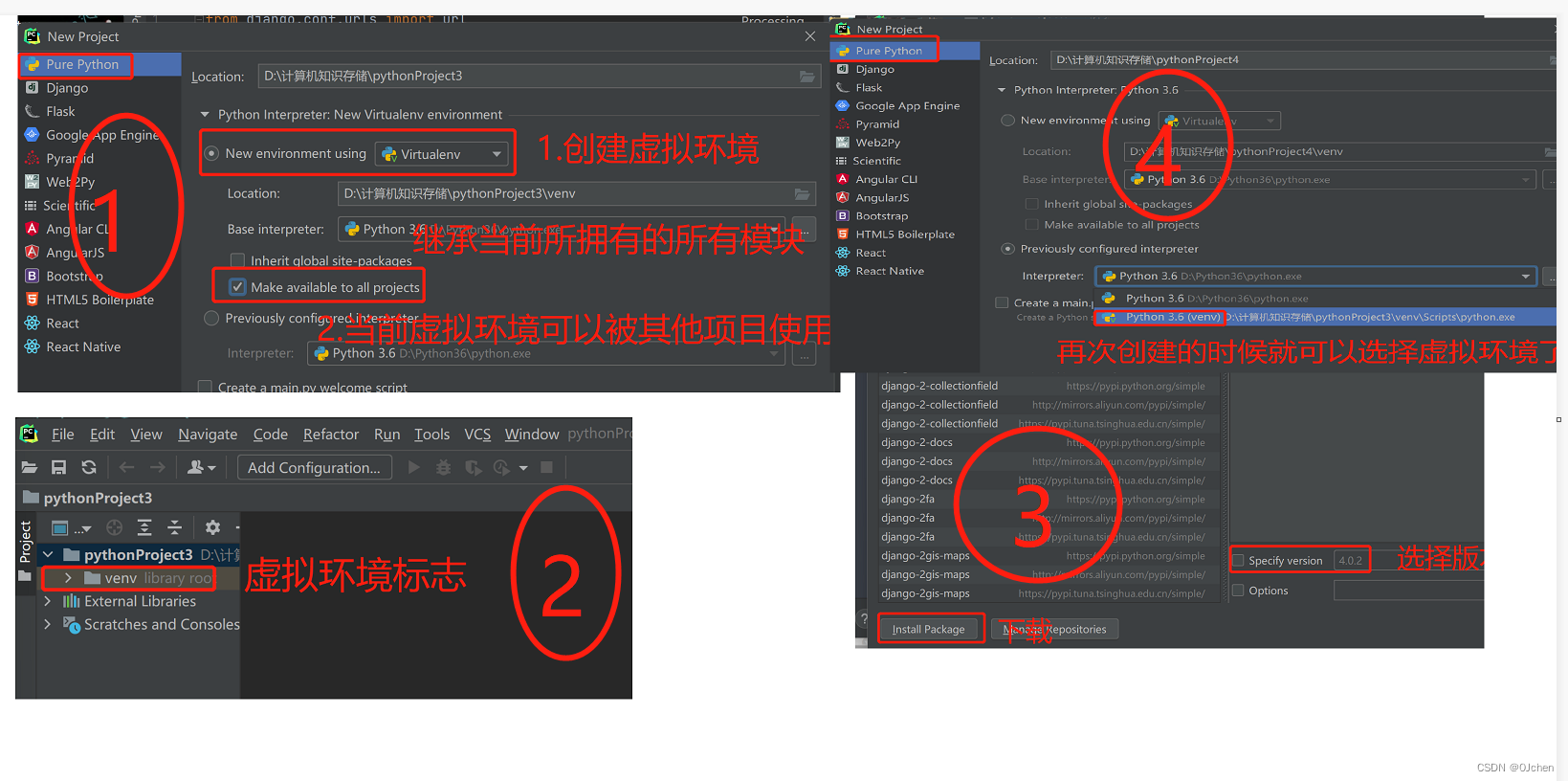
文章目录 路由匹配语法路由配置注意事项转换器注册自定义转化器 无名分组和有名分组无名分组有名分组 反向解析简介普通反向解析无名分组、有名分组之反向解析 路由分发简介为什么要用路由分发?路由分发实现 伪静态的概念名称空间虚拟环境什么是虚拟环境?…...
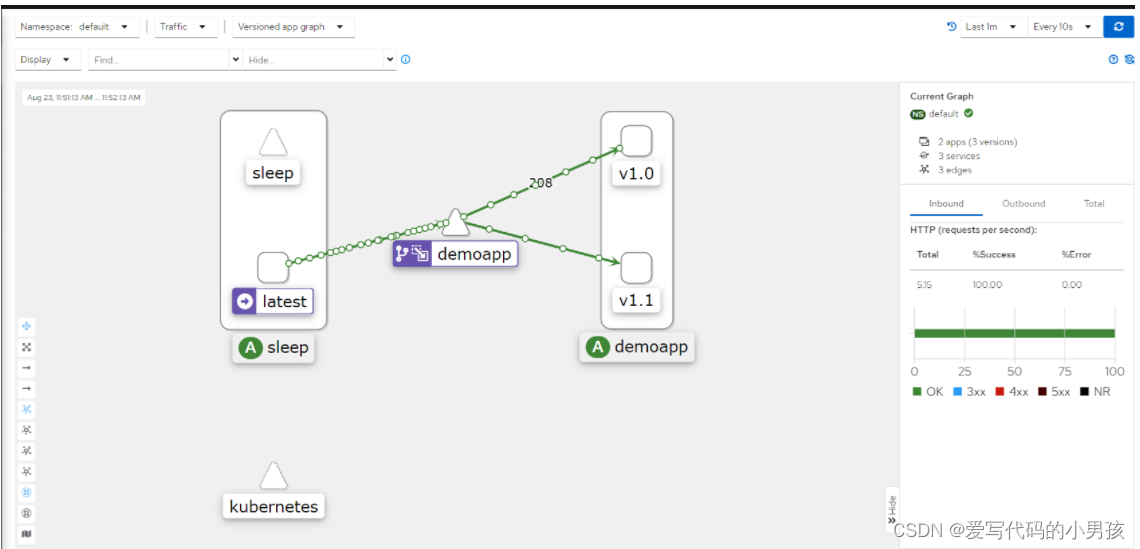
【06】VirtualService高级流量功能
5.3 weight 部署demoapp v10和v11版本 --- apiVersion: apps/v1 kind: Deployment metadata:labels:app: demoappv10version: v1.0name: demoappv10 spec:progressDeadlineSeconds: 600replicas: 3selector:matchLabels:app: demoappversion: v1.0template:metadata:labels:app…...

322. 零钱兑换
给你一个整数数组 coins ,表示不同面额的硬币;以及一个整数 amount ,表示总金额。 计算并返回可以凑成总金额所需的 最少的硬币个数 。如果没有任何一种硬币组合能组成总金额,返回 -1 。 你可以认为每种硬币的数量是无限的。 示…...
【大模型-第一篇】在阿里云上部署ChatGLM3
前言 好久没写博客了,最近大模型盛行,尤其是ChatGLM3上线,所以想部署试验一下。 本篇只是第一篇,仅仅只是部署而已,没有FINETUNE、没有Langchain更没有外挂知识库,所以从申请资源——>开通虚机——>…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...
)
论文解读:交大港大上海AI Lab开源论文 | 宇树机器人多姿态起立控制强化学习框架(二)
HoST框架核心实现方法详解 - 论文深度解读(第二部分) 《Learning Humanoid Standing-up Control across Diverse Postures》 系列文章: 论文深度解读 + 算法与代码分析(二) 作者机构: 上海AI Lab, 上海交通大学, 香港大学, 浙江大学, 香港中文大学 论文主题: 人形机器人…...

CTF show Web 红包题第六弹
提示 1.不是SQL注入 2.需要找关键源码 思路 进入页面发现是一个登录框,很难让人不联想到SQL注入,但提示都说了不是SQL注入,所以就不往这方面想了 先查看一下网页源码,发现一段JavaScript代码,有一个关键类ctfs…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

AI Agent与Agentic AI:原理、应用、挑战与未来展望
文章目录 一、引言二、AI Agent与Agentic AI的兴起2.1 技术契机与生态成熟2.2 Agent的定义与特征2.3 Agent的发展历程 三、AI Agent的核心技术栈解密3.1 感知模块代码示例:使用Python和OpenCV进行图像识别 3.2 认知与决策模块代码示例:使用OpenAI GPT-3进…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...
安装docker)
Linux离线(zip方式)安装docker
目录 基础信息操作系统信息docker信息 安装实例安装步骤示例 遇到的问题问题1:修改默认工作路径启动失败问题2 找不到对应组 基础信息 操作系统信息 OS版本:CentOS 7 64位 内核版本:3.10.0 相关命令: uname -rcat /etc/os-rele…...

【Linux】自动化构建-Make/Makefile
前言 上文我们讲到了Linux中的编译器gcc/g 【Linux】编译器gcc/g及其库的详细介绍-CSDN博客 本来我们将一个对于编译来说很重要的工具:make/makfile 1.背景 在一个工程中源文件不计其数,其按类型、功能、模块分别放在若干个目录中,mak…...
:工厂方法模式、单例模式和生成器模式)
上位机开发过程中的设计模式体会(1):工厂方法模式、单例模式和生成器模式
简介 在我的 QT/C 开发工作中,合理运用设计模式极大地提高了代码的可维护性和可扩展性。本文将分享我在实际项目中应用的三种创造型模式:工厂方法模式、单例模式和生成器模式。 1. 工厂模式 (Factory Pattern) 应用场景 在我的 QT 项目中曾经有一个需…...
