【JUC】三、集合的线程安全
文章目录
- 1、ArrayList集合线程安全问题分析
- 2、解决方式一:Vector或synchronizedList( )
- 3、解决方式二:CopyOnWriteArrayList 写时复制
- 4、HashSet集合线程不安全的分析与解决
- 5、HashMap集合线程不安全的分析与解决
1、ArrayList集合线程安全问题分析
对List集合非线程安全的Demo代码:
public class ArrayListDemo {public static void main(String[] args) {List<String> list = new ArrayList<>();//多个线程同时写入List集合for (int i = 0; i < 10; i++) {new Thread(() -> {//加元素list.add(UUID.randomUUID().toString().substring(0,8));//遍历输出集合System.out.println(list);},String.valueOf(i)).start();}}
}
运行:

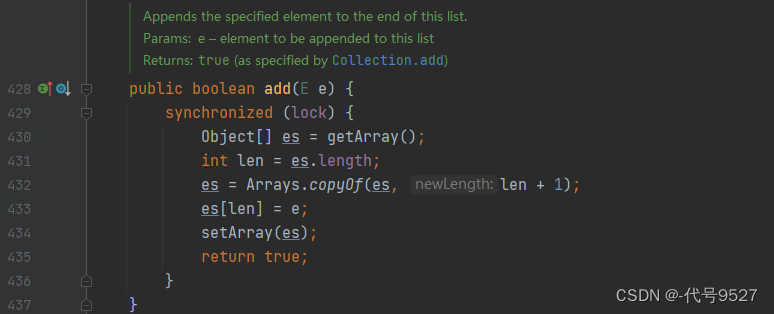
ConcurrentModificationException异常,是在多线程环境下,当一个线程正在遍历集合,而另一个线程对集合进行了修改操作时,就会抛出这个异常。以ArrayList为例,其add方法源码,未加synchronized关键字:
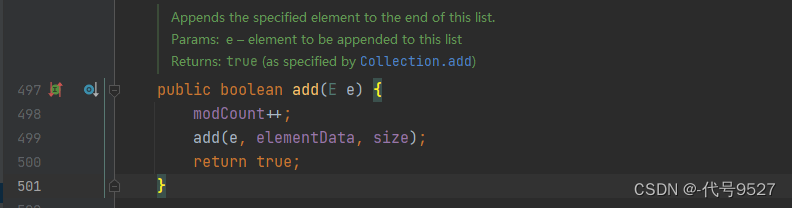
再点击报错详情,进入抛出异常的方法:
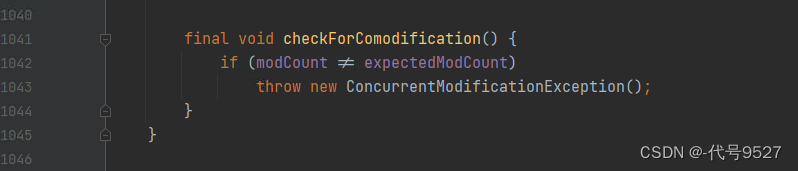
modCount即集合新增的次数,是实际修改次数,而expectedModCount是预期修改次数,它是ArrayList的一个内部类Itr的成员变量,调用iterator()获取迭代器时,内部创建Itr对象,此时,modCount会赋值给expectedModCount:
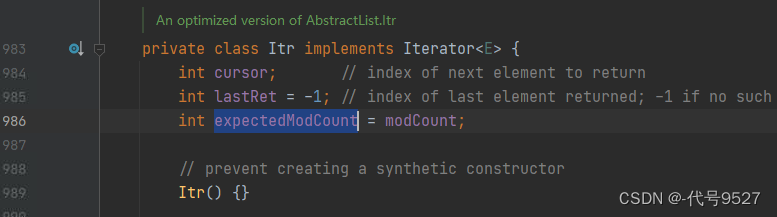
拿到迭代器对象,要遍历集合时,modCount已经赋值给expectedModCount,而此时其他线程继续add,modCount+1,modCount和expectedModCount就不相等了。
2、解决方式一:Vector或synchronizedList( )
List接口的另一个实现类Vector,其add方法加了关键字,使用它可解决线程安全问题,但很古老了,since1.2,很少用了。
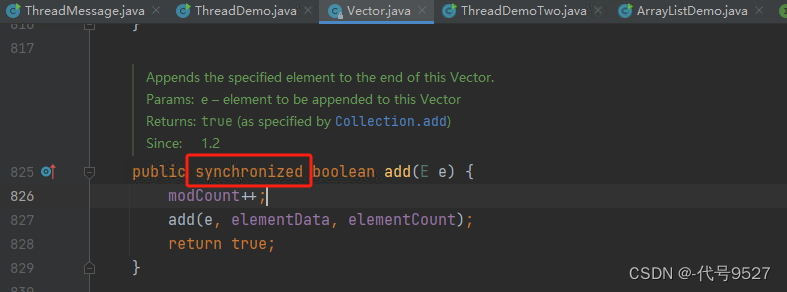
List<String> list = new Vector<>();
//重复代码略
同样一种古老的解决方案,可以用Collections的synchronizedList方法,传入一个有线程安全问题的List,如ArrayList:
List<String> list = Collections.synchronizedList(new ArrayList<>());
3、解决方式二:CopyOnWriteArrayList 写时复制
List<String> list = new CopyOnWriteArrayList<>();
完整demo:
public class ArrayListDemo {public static void main(String[] args) {List<String> list = new CopyOnWriteArrayList<>();//多个线程同时写入List集合for (int i = 0; i < 10; i++) {new Thread(() -> {//加元素list.add(UUID.randomUUID().toString().substring(0,8));//遍历输出集合System.out.println(list);},String.valueOf(i)).start();}}
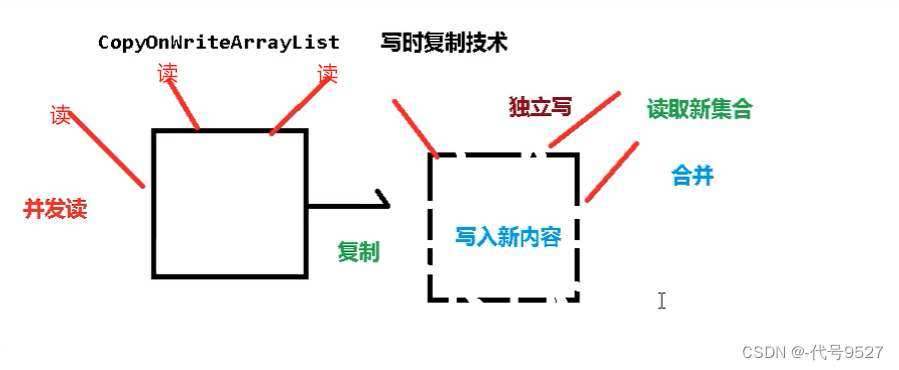
}原理是写时复制技术,即:
- 对这个List实现类的集合,可以多线程并发读
- 往集合中写的时候,则只能独立写,先复制一份原来的集合,这个时候读还是读原来的,然后往新集合里面写入新的内容
- 写完后新旧合并,再读时,就读这个合并后的集合
看下源码,再对照着理解写时复制:
4、HashSet集合线程不安全的分析与解决
public class HashSetDemo {public static void main(String[] args) {Set<String> set = new HashSet<>();for (int i = 0; i < 30; i++) {new Thread(() -> {//写入set.add(UUID.randomUUID().toString().substring(0,8));//读System.out.println(set);},String.valueOf(i)).start();}}
}
运行:
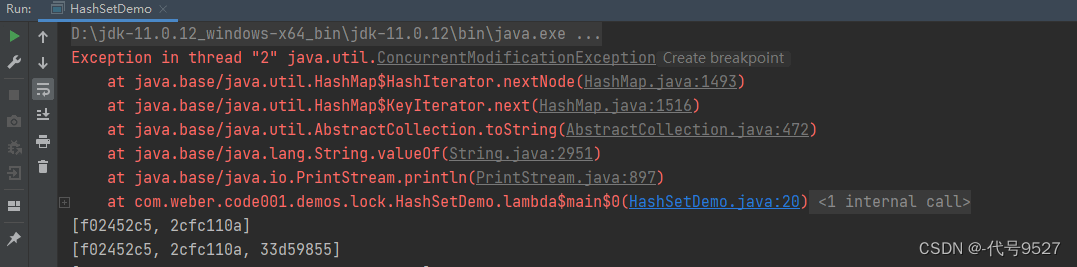
解决办法类比上面的List,使用CopyOnWriteArraySet:
Set<String> set = new CopyOnWriteArraySet<>();
5、HashMap集合线程不安全的分析与解决
public class HashSetDemo {public static void main(String[] args) {Map<String,string> map = new HashMap<>();for (int i = 0; i < 30; i++) {String key = String.valueOf(i);new Thread(() -> {//写入map.put(key,UUID.randomUUID().toString().substring(0,8));//读System.out.println(map);},String.valueOf(i)).start();}}
}
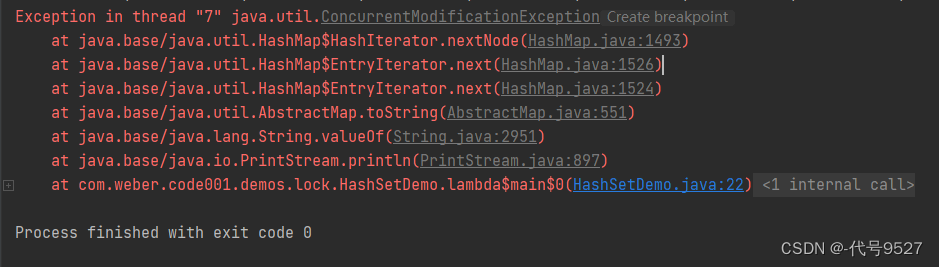
解决办法类比List,用ConcurrentHashMap:
Map<String,String> map = new ConcurrentHashMap<>();
相关文章:

【JUC】三、集合的线程安全
文章目录 1、ArrayList集合线程安全问题分析2、解决方式一:Vector或synchronizedList( )3、解决方式二:CopyOnWriteArrayList 写时复制4、HashSet集合线程不安全的分析与解决5、HashMap集合线程不安全的分析与解决 1、ArrayList集合线程安全问题分析 对…...
使用 Redis 实现生成分布式全局唯一ID(使用SpringBoot环境实现)
目录 一、前言二、如何通过Redis设计一个分布式全局唯一ID生成工具2.1、使用 Redis 计数器实现2.2、使用 Redis Hash结构实现 三、通过代码实现分布式全局唯一ID工具3.1、编写获取工具3.2、测试获取工具 四、总结 一、前言 在很多项目中生成类似订单编号、用户编号等有唯一性数…...
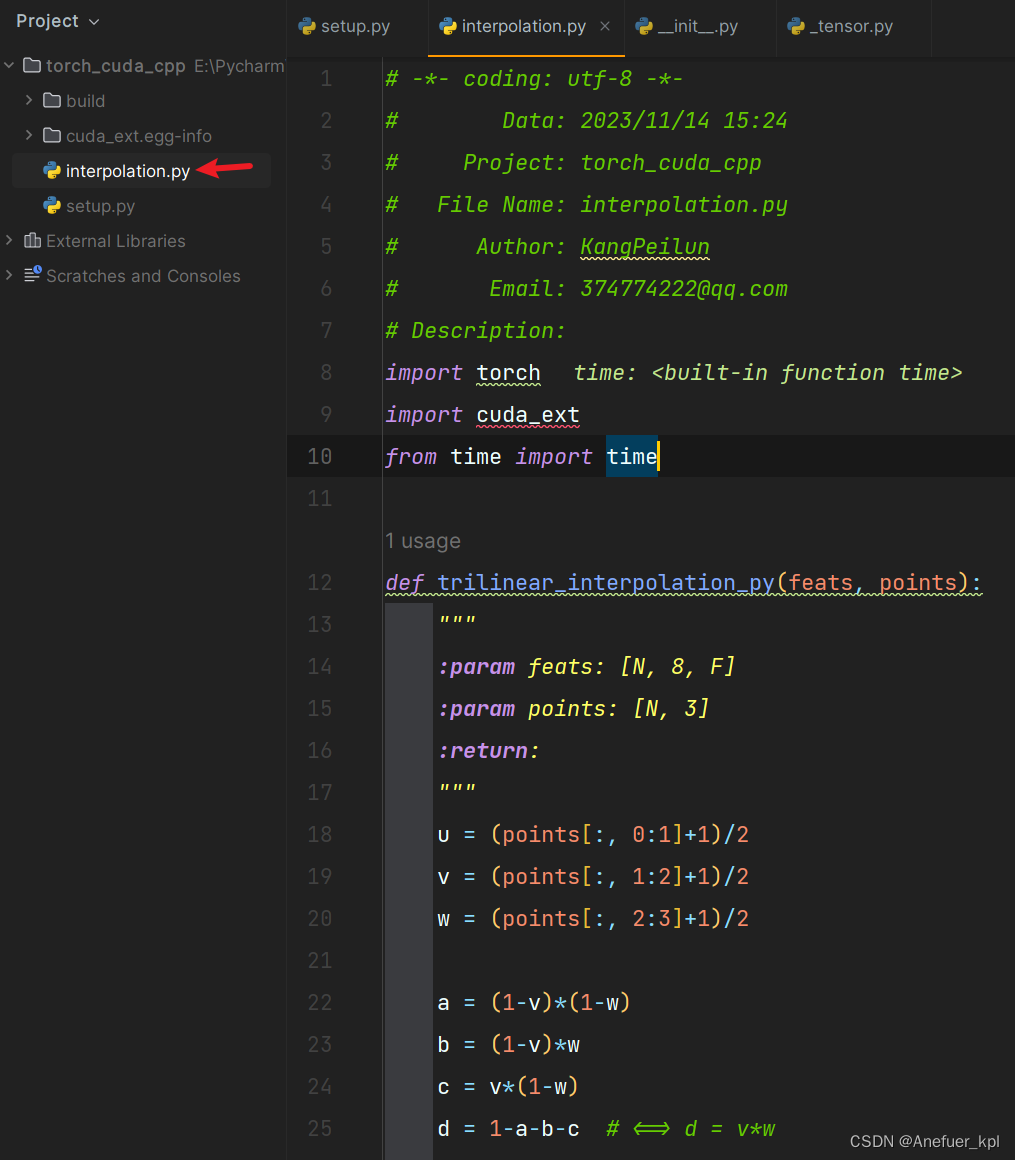
Pytorch CUDA CPP简易教程,在Windows上操作
文章目录 前言一、使用的工具二、学习资源分享三、libtorch环境配置1.配置CUDA、nvcc、cudnn2.下载libtorch3.CLion配置libtorch4.CMake Application指定Environment variables5.测试libtorch 四、PyTorch CUDA CPP项目流程1.使用CLion结合torch extension编写可以调用cuda的C代…...

服务器怎么连接
服务器怎么连接 服务器可以通过多种方式连接,主要取决于服务器的操作系统、网络配置和连接方式等因素。 1. SSH连接:如果服务器使用的是Linux操作系统,可以通过SSH协议连接。需要使用SSH客户端工具,例如PuTTY,在登录页…...
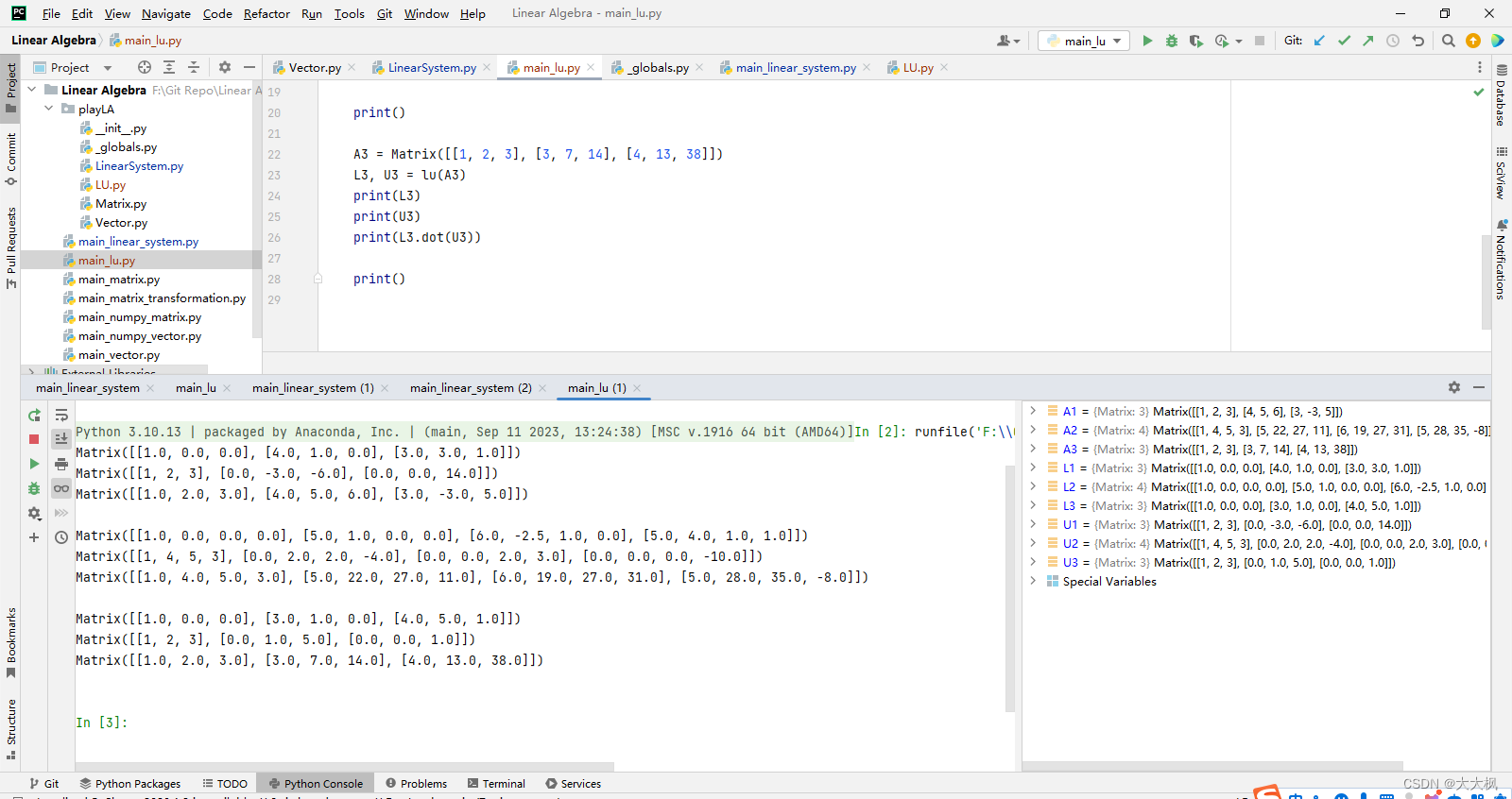
线性代数-Python-05:矩阵的逆+LU分解
文章目录 1 矩阵的逆1.1 求解矩阵的逆 2 初等矩阵2.1 初等矩阵和可逆性 3 矩阵的LU分解3.1 LU分解的实现 1 矩阵的逆 1.1 求解矩阵的逆 def inv(A):if A.row_num() ! A.col_num():return Nonen A.row_num()"""矩阵A单位矩阵"""ls LinearSyste…...

shell实用脚本命令
1. declare declare 命令是一个非常常用的命令之一,它可以用来声明变量的类型和属性,比如变量的作用域、是否只读等等。 一、declare命令的基本用法 declare 命令可以用来声明变量,其最基本的用法如下:declare 变量名 在上面的命…...
STM32——端口复用与重映射概述与配置(HAL库)
文章目录 前言一、什么是端口复用?什么是重映射?有什么区别?二、端口复用配置 前言 本篇文章介绍了在单片机开发过程中使用的端口复用与重映射。做自我学习的简单总结,不做权威使用,参考资料为正点原子STM32F1系列精英…...
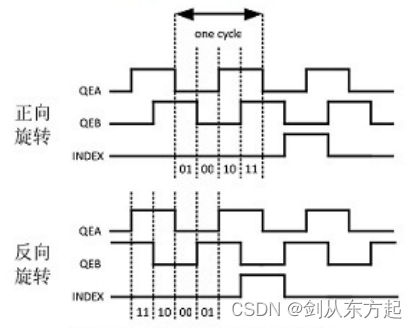
ABZ正交编码 - 异步电机常用的位置信息确定方式
什么是正交编码? ab正交编码器(又名双通道增量式编码器),用于将线性移位转换为脉冲信号。通过监控脉冲的数目和两个信号的相对相位,用户可以跟踪旋转位置、旋转方向和速度。另外,第三个通道称为索引信号&am…...
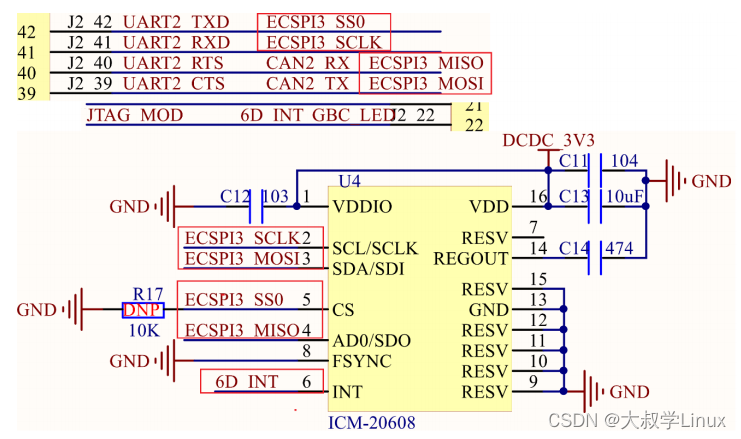
Linux学习第41天:Linux SPI 驱动实验(二):乾坤大挪移
Linux版本号4.1.15 芯片I.MX6ULL 大叔学Linux 品人间百味 思文短情长 本章的思维导图如下: 二、I.MX6U SPI主机驱动分析 主机驱动一般都是由SOC厂商写好的。不作为重点需要掌握的内容。 三、SPI设备驱动编写流程 1、SP…...
黑客泄露 3500 万条 LinkedIn 用户记录
被抓取的 LinkedIn 数据库分为两部分泄露:一部分包含 500 万条用户记录,第二部分包含 3500 万条记录。 LinkedIn 数据库保存了超过 3500 万用户的个人信息,被化名 USDoD 的黑客泄露。 该数据库在臭名昭著的网络犯罪和黑客平台 Breach Forum…...
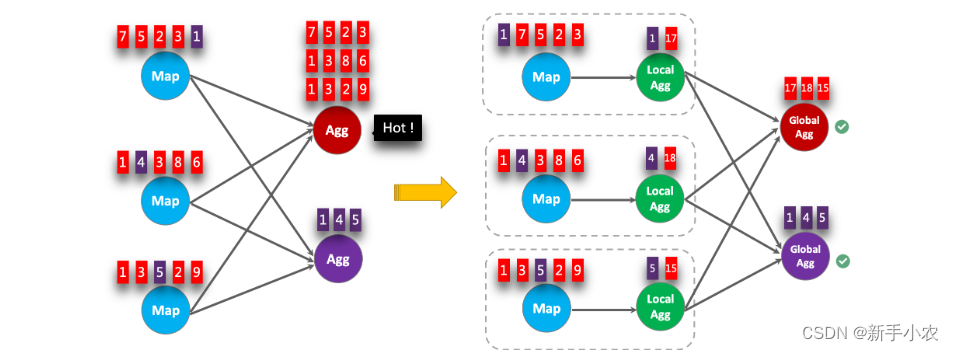
Flink SQL -- 反压
1、测试反压: 1、反压: 指的是下游消费数据的速度比上游产生数据的速度要小时会出现反压,下游导致上游的Task反压。 2、测试反压:使用的是DataGen CREATE TABLE words (word STRING ) WITH (connector datagen,rows-per-second…...
快速入门安装及使用git与svn的区别常用命令
一、导言 1、什么是svn? SVN是Subversion的简称,是一个集中式版本控制系统。与Git不同,SVN没有分布式的特性。在SVN中,项目的代码仓库位于服务器上,团队成员通过向服务器提交和获取代码来实现版本控制。SVN记录了每个…...

超详细介绍如何使用 OpenCV 和 BGS 库进行背景扣除
深入研究这些 CV 系统背后的想法,我们可以观察到,在大多数情况下,初始步骤包含背景减除 (BS),这有助于获得视频流中对象的相对粗略和快速的识别,以便对其进行进一步的精细处理。在当前的文章中,我们将介绍几种在准确性和处理时间 BS 方法方面值得注意的算法:SuBSENSE和基…...

STM32F4、GD32F4 内部硬件CRC使用方法和踩坑实录
背景 某项目用到了IC卡刷卡启动功能,程序中对读取IC卡的相关数据后要进行CRC校验,本文介绍如何在STM32F4 GD32F4 平台上使用标准库函数进行CRC硬件校验。 摘要 本文介绍如何在STM32F4、GD32F4 平台上使用标准库函数进行CRC硬件校验。包括容易出现的问题和解决方法。涉及STM3…...
【SpringBoot】序列化和反序列化介绍
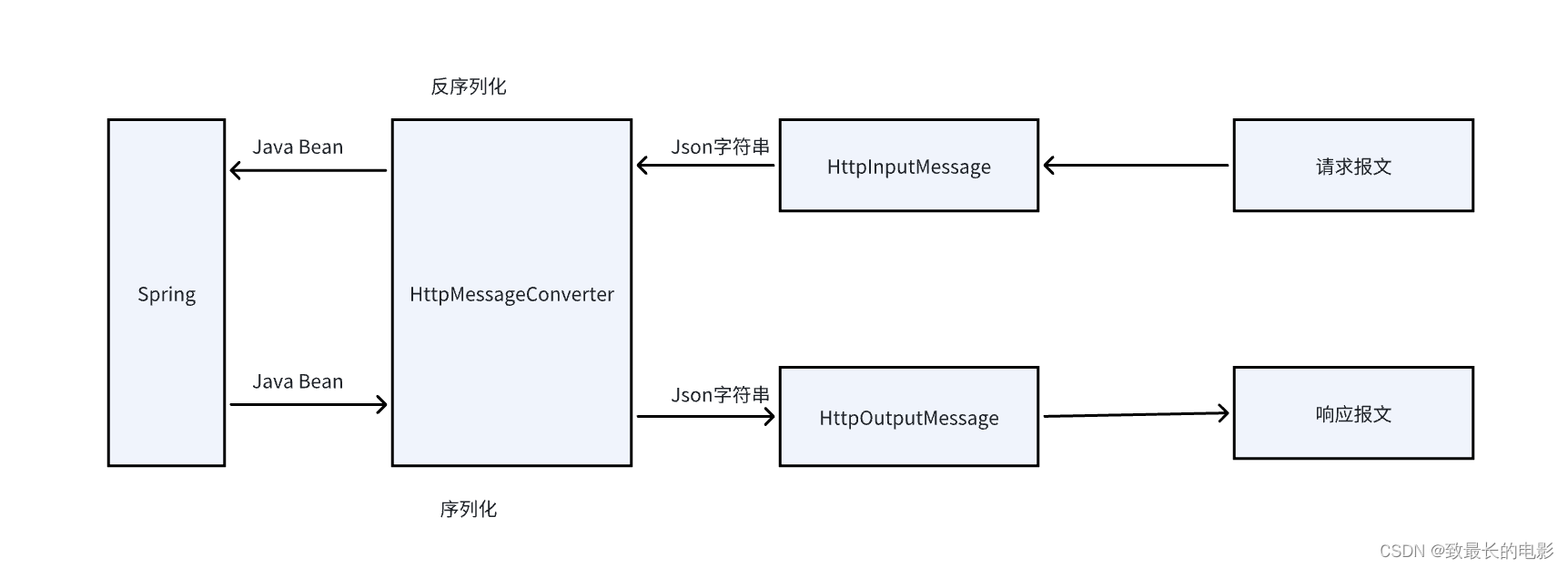
一、认识序列化和反序列化 Serialization(序列化)是一种将对象以一连串的字节描述的过程;deserialization(反序列化)是一种将这些字节重建成一个对象的过程。将程序中的对象,放入文件中保存就是序列化&…...

Android 升级软件后清空工厂模式测试进度
Android 升级软件后清空工厂模式测试进度 最近收到项目需求反馈:升级软件后,进入工厂模式测试项,界面显示测试项保留了升级前的测试状态(有成功及失败),需修改升级软件后默认清空测试项测试状态,具体修改参照如下: /…...

Promise原理、以及Promise.race、Promise.all、Promise.resolve、Promise.reject实现;
为了向那道光亮奔过去,他敢往深渊里跳; 于是今天朝着Promise的实现前进吧,写了四个小时,终于完结撒花; 我知道大家没有耐心,当然我也坐的腰疼,直接上代码,跟着我的注释一行行看过去…...
)
mysql---MHA(高可用)
MHA概述 magterhight availabulity :基于主库的高可用环境下,主故障切换基础要求:主从架构 (一主两从)解决mysql的单点故障问题,一旦数据库崩溃,MHA会在0-30s内这东东完成故障切换。复制方式:半…...
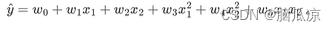
人工智能基础_机器学习032_多项式回归升维_原理理解---人工智能工作笔记0072
现在开始我们来看多项式回归,首先理解多维 原来我们学习的使用线性回归,其实就是一条直线对吧,那个是一维的,我们之前学的全部都是一维的对吧,是一维的,然后是多远的,因为有多个x1,x2,x3,x4... 但是比如我们有一个数据集,是上面这种,的如果用一条直线很难拟合,那么 这个时候,…...

C#截取范围
string[] strs new string[]{"1e2qe","23123e21","3ewqewq","4fewfew","5fsdfds"};var list strs[1..2];Range p 0..3;var list strs[Range];...

《从零掌握MIPI CSI-2: 协议精解与FPGA摄像头开发实战》-- CSI-2 协议详细解析 (一)
CSI-2 协议详细解析 (一) 1. CSI-2层定义(CSI-2 Layer Definitions) 分层结构 :CSI-2协议分为6层: 物理层(PHY Layer) : 定义电气特性、时钟机制和传输介质(导线&#…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

【无标题】路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论
路径问题的革命性重构:基于二维拓扑收缩色动力学模型的零点隧穿理论 一、传统路径模型的根本缺陷 在经典正方形路径问题中(图1): mermaid graph LR A((A)) --- B((B)) B --- C((C)) C --- D((D)) D --- A A -.- C[无直接路径] B -…...

MFC 抛体运动模拟:常见问题解决与界面美化
在 MFC 中开发抛体运动模拟程序时,我们常遇到 轨迹残留、无效刷新、视觉单调、物理逻辑瑕疵 等问题。本文将针对这些痛点,详细解析原因并提供解决方案,同时兼顾界面美化,让模拟效果更专业、更高效。 问题一:历史轨迹与小球残影残留 现象 小球运动后,历史位置的 “残影”…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

【UE5 C++】通过文件对话框获取选择文件的路径
目录 效果 步骤 源码 效果 步骤 1. 在“xxx.Build.cs”中添加需要使用的模块 ,这里主要使用“DesktopPlatform”模块 2. 添加后闭UE编辑器,右键点击 .uproject 文件,选择 "Generate Visual Studio project files",重…...

快速排序算法改进:随机快排-荷兰国旗划分详解
随机快速排序-荷兰国旗划分算法详解 一、基础知识回顾1.1 快速排序简介1.2 荷兰国旗问题 二、随机快排 - 荷兰国旗划分原理2.1 随机化枢轴选择2.2 荷兰国旗划分过程2.3 结合随机快排与荷兰国旗划分 三、代码实现3.1 Python实现3.2 Java实现3.3 C实现 四、性能分析4.1 时间复杂度…...

鸿蒙HarmonyOS 5军旗小游戏实现指南
1. 项目概述 本军旗小游戏基于鸿蒙HarmonyOS 5开发,采用DevEco Studio实现,包含完整的游戏逻辑和UI界面。 2. 项目结构 /src/main/java/com/example/militarychess/├── MainAbilitySlice.java // 主界面├── GameView.java // 游戏核…...

2.2.2 ASPICE的需求分析
ASPICE的需求分析是汽车软件开发过程中至关重要的一环,它涉及到对需求进行详细分析、验证和确认,以确保软件产品能够满足客户和用户的需求。在ASPICE中,需求分析的关键步骤包括: 需求细化:将从需求收集阶段获得的高层需…...

Pandas 可视化集成:数据科学家的高效绘图指南
为什么选择 Pandas 进行数据可视化? 在数据科学和分析领域,可视化是理解数据、发现模式和传达见解的关键步骤。Python 生态系统提供了多种可视化工具,如 Matplotlib、Seaborn、Plotly 等,但 Pandas 内置的可视化功能因其与数据结…...
