C++实现ransac
目录
一、ransac算法原理
1.1、算法概念
1.2、图解
二、c++实现ransac
2.1、设置随机样本和离群点
2.2、随机抽取样本
2.3、内点计算
2.4、更新参数
2.2、完整代码
一、ransac算法原理
1.1、算法概念
随机抽样一致性 (RANSAC) 是一种迭代方法,用于根据一组包含异常值的观测数据来估计数学模型的参数,此时异常值不会对估计值产生影响。 因此,它也可以解释为一种异常值检测方法,说白了就是能剔除异常的、离群的样本。 它是一种非确定性算法,因为它仅以一定的概率产生合理的结果,并且随着允许更多迭代,该概率会增加,说白了就是由于每次随机抽取样本,最终都会得到更好的结果,但是每次执行整个ransac算法,最终结果会有略微差异。 该算法最初由 Fischler 和 Bolles 在 SRI International 于 1981 年发布。他们使用 RANSAC 来解决位置确定问题 (LDP),其目标是确定空间中投影到图像上的点,形成一组地标 已知地点。
一个基本假设是数据由“内点”和“离群值”组成,“内点”是指其分布可以通过某些模型参数集来解释的数据,尽管可能会受到噪声的影响;“离群值”是不适合模型的数据。 例如,异常值可能来自噪声的极值、错误的测量或有关数据解释的错误假设。 RANSAC 还假设,给定一组(通常很小的)内点,存在一个可以估计模型参数的过程,该模型可以最佳地解释或拟合该数据。
伪代码:
Given:data – a set of observationsmodel – a model to explain observed data pointsn – minimum number of data points required to estimate model parametersk – maximum number of iterations allowed in the algorithmt – threshold value to determine data points that are fit well by modeld – number of close data points required to assert that a model fits well to dataReturn:bestFit – model parameters which best fit the data (or nul if no good model is found)iterations = 0
bestFit = nul
bestErr = something really large
while iterations < k {maybeInliers = n randomly selected values from datamaybeModel = model parameters fitted to maybeInliersalsoInliers = empty setfor every point in data not in maybeInliers {if point fits maybeModel with an error smaller than tadd point to alsoInliers}if the number of elements in alsoInliers is > d {% this implies that we may have found a good model% now test how good it isbetterModel = model parameters fitted to all points in maybeInliers and alsoInliersthisErr = a measure of how well betterModel fits these pointsif thisErr < bestErr {bestFit = betterModelbestErr = thisErr}}increment iterations
}
return bestFit1.2、图解
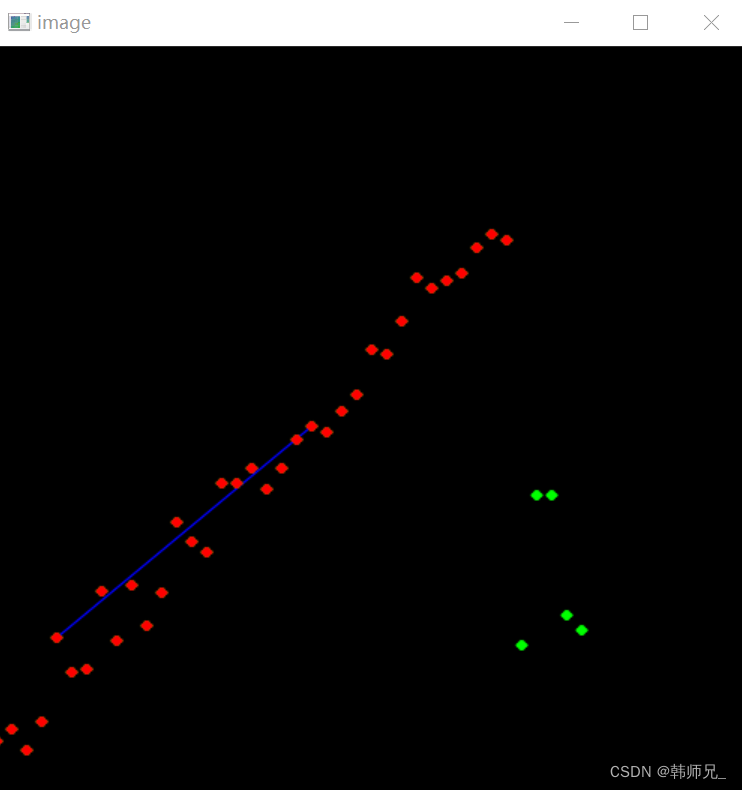
如下图,以直线拟合为例子,假如给定N个点,求解直线方程y=kx+b。这里使用ransac算法求解直线方程参数k、b,主要思想如下:
- step1:随机选取两个样本点,如图红点
- step2:计算直线方程参数ki、bi,得到直线记为Li,此时有k=ki,b=bi
- step3:计算其余所有点到直线Li的距离,距离Li足够近的点为内点(inliers),比较远的点为外点(outliers)
- step4:执行step1、step2得到直线Lj(对应方程参数kj、bj);执行step3得到的inliers如果大于直线Li,那么更新参数为:k=kj,b=bj。
依次类推,最多循环迭代100次,只要下一次计算得到直线比上一次更优,那就更新参数k、b;直到内点比例足够高或者循环到100次了为止。

二、c++实现ransac
依赖opencv的一点点数据结构,你也可以自己去掉。
2.1、设置随机样本和离群点
如下图,红色点就是样本点,绿色的就是离群点
// time seed
srand((unsigned int)time(nullptr));
// <1>产生随机数
vector<Point2d> points;
// 精确解
const int k = 1;
const int b = 10;// x [0, 390]; y [10, 400] total_numbers = 40
for (int x = 0; x < 400; x += 10)
{points.push_back(Point2d(x, k * x + b + Ransac::getRand(0, 60)));
}
//添加离群点
points[35].y = 100;
points[36].y = 200;
points[37].y = 200;
points[38].y = 120;
points[39].y = 110;2.2、随机抽取样本
随机选取两个样本点的索引。
// <1>、随机抽取两个样本
int index_first = Ransac::getRand(0, points.size() - 2);
int index_second = Ransac::getRand(0, points.size() - 2);
sample_first = points[index_first];
sample_second = points[index_second];2.3、内点计算
y_error实在计算点到直线距离,如果小于y_threshold,也就是内点inliers。
// <2>、根据距离,来找出所有样本点中的内点,并统计数量
for (int i = 0; i < points.size(); i++)
{// delta = k * x + b - ydouble y_error = abs(k_estimate * points[i].x + b_estimate - points[i].y) / sqrt((pow(k_estimate, 2) + 1));//cout << "y_error = " << y_error << endl;if (y_error < y_threshold){count++;}
}2.4、更新参数
如果当前迭代比上一轮内点要多,那直接当当前迭代对应参数更新为最优解
// <3>、找出内点数量最多的那一组
if (count > total)
{total = count;best_sample_first = sample_first;best_sample_second = sample_second;best_parameters.x = k_estimate;best_parameters.y = b_estimate;
}2.2、完整代码
需要说明:
- ransac每次结果不一样,但是总是能计算得到好的解;
- 以下代码在画直线的时候没有画得很长,并不影响算法,只是懒得画而已。

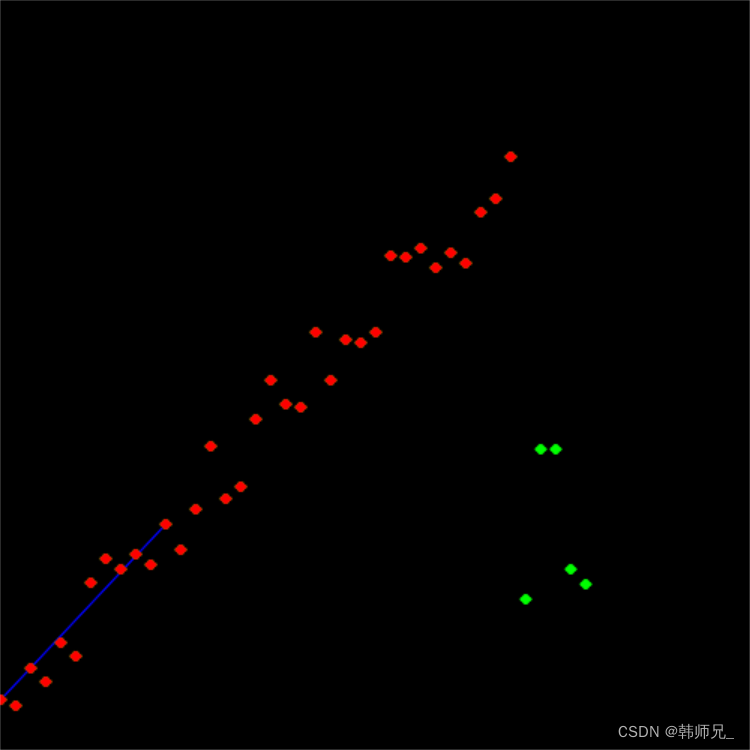
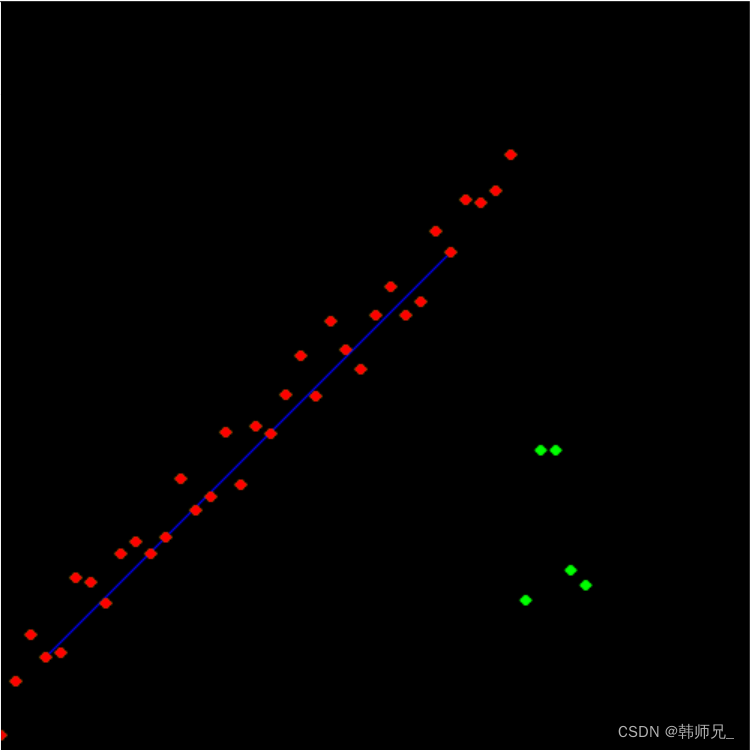
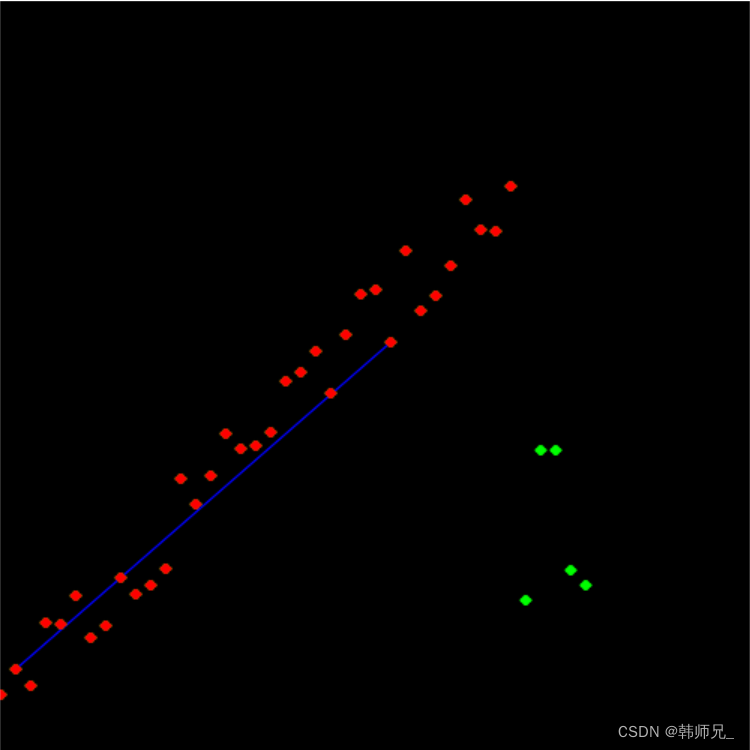
完整代码:
#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<vector>
#include<algorithm>
#include<ctime>
using namespace std;
#include<opencv2/opencv.hpp>
using namespace cv;
// 功能:画点
void drawPoints(vector<Point2d> points, Mat& image, bool is_green)
{if (is_green){for (int i = 0; i < points.size(); i++){circle(image, Point2i(int(points[i].x), int(points[i].y)), 2, cv::Scalar(0, 255, 0), 2, LINE_AA);}}else{for (int i = 0; i < points.size(); i++){circle(image, Point2i(int(points[i].x), int(points[i].y)), 2, cv::Scalar(0, 0, 255), 2, LINE_AA);}}}
// 功能:画线
void drawLine(Point2d begin, Point2d end, Mat& image)
{line(image, Point2i(int(begin.x), int(begin.y)),Point2i(int(end.x), int(end.y)), Scalar(255, 0, 0), 1, LINE_AA);
}
// 功能:将一张图经行纵向镜像
void upDownMirror(Mat& image)
{Mat image_cpy = image.clone();for (int j = 0; j < image.rows; j++){for (int i = 0; i < image.cols; i++){image.ptr<cv::Vec3b>(j)[i] = image_cpy.ptr<cv::Vec3b>(image.rows - 1 - j)[i];}}
}
// 功能:最简单的直线拟合 Ransac 框架
class Ransac
{
public:Ransac(vector<double> x, vector<double> y);~Ransac();static int getRand(int min, int max);//[min, min + max - 1]
public:vector<double> x_, y_;
};Ransac::Ransac(vector<double> x, vector<double> y) :x_(x), y_(y)
{}Ransac::~Ransac()
{}int Ransac::getRand(int min, int max)//[min, min + max - 1]
{return rand() % max + min;
}int main()
{// time seedsrand((unsigned int)time(nullptr));// <1>产生随机数vector<Point2d> points;// 精确解const int k = 1;const int b = 10;// x [0, 390]; y [10, 400] total_numbers = 40for (int x = 0; x < 400; x += 10){points.push_back(Point2d(x, k * x + b + Ransac::getRand(0, 60)));}//添加离群点points[35].y = 100;points[36].y = 200;points[37].y = 200;points[38].y = 120;points[39].y = 110;const int itr_nums = 300;double k_estimate = 0;double b_estimate = 0;Point2d best_parameters; // [k, b]// 统计纵向距离 yint count = 0; // 内点计数器int y_threshold = 50; // 判定内点的阈值int total = 0; // 内点总数//样本点Point2d sample_first;Point2d sample_second;// 最佳样本点Point2d best_sample_first;Point2d best_sample_second;for (int i = 0; i < itr_nums; i++){// <1>、随机抽取两个样本int index_first = Ransac::getRand(0, points.size() - 2);int index_second = Ransac::getRand(0, points.size() - 2);sample_first = points[index_first];sample_second = points[index_second];if (sample_first == sample_second){continue;}// 计算斜率 k = (y2 - y1)/(x2 - x1)k_estimate = (sample_second.y - sample_first.y) / (sample_second.x - sample_first.x);// 计算截距 b = y1 - k * x1b_estimate = sample_first.y - k_estimate * sample_first.x;// <2>、根据距离,来找出所有样本点中的内点,并统计数量for (int i = 0; i < points.size(); i++){// delta = k * x + b - ydouble y_error = abs(k_estimate * points[i].x + b_estimate - points[i].y) / sqrt((pow(k_estimate, 2) + 1));//cout << "y_error = " << y_error << endl;if (y_error < y_threshold){count++;}}// <3>、找出内点数量最多的那一组if (count > total){total = count;best_sample_first = sample_first;best_sample_second = sample_second;best_parameters.x = k_estimate;best_parameters.y = b_estimate;}count = 0;}cout << "内点数 = " << total << endl;cout << "斜率 k = " << best_parameters.x << "截距 b = " << best_parameters.y << endl;// 统计内点vector<Point2d> inliners_points;for (int i = 0; i < points.size(); i++){// delta = k * x + b - ydouble y_error = abs(best_parameters.x * points[i].x + best_parameters.y - points[i].y) / sqrt((pow(k_estimate, 2) + 1));//cout << "y_error = " << y_error << endl;if (y_error < y_threshold){inliners_points.push_back(points[i]);}}Mat image = Mat::zeros(500, 500, CV_8UC3);drawLine(best_sample_first, best_sample_second, image);drawPoints(points, image, true);drawPoints(inliners_points, image, false); //画内点upDownMirror(image);imshow("image", image);waitKey(0);return 1;
}相关文章:

C++实现ransac
目录 一、ransac算法原理 1.1、算法概念 1.2、图解 二、c实现ransac 2.1、设置随机样本和离群点 2.2、随机抽取样本 2.3、内点计算 2.4、更新参数 2.2、完整代码 一、ransac算法原理 1.1、算法概念 随机抽样一致性 (RANSAC) 是一种迭代方法,用于根据一组包…...
DNS域名解析服务
1.概述 1.1.产生原因 IP 地址:是互联网上计算机唯一的逻辑地址,通过IP 地址实现不同计算机之间的相互通信,每台联网计算机都需要通过I 地址来互相联系和分别,但由于P 地址是由一串容易混淆的数字串构成,人们很难记忆所有计算机的…...
【milkv】2、mpu6050驱动添加及测试
前言 本章介绍mpu6050的驱动添加以及测试。 其中驱动没有采用sdk提供的驱动,一方面需要配置irq,另一方面可以学习下如何通过ko方式添加驱动。 一、参考文章 驱动及测试文件编译流程: https://community.milkv.io/t/risc-v-milk-v-lsm6ds…...
SpringCloud Alibaba(中):服务熔断降级-Sentinel
Sentinel Sentinel是阿里巴巴开源的分布式系统流量防卫防护组件,主要对分布式系统中的流量进行控制、熔断降级等保护操作。Sentinel的目标是成为互联网级别分布式系统的流量防卫防护组件,它与系统的各个部分集成,保护着系统的入口和出口。 …...

模型的训练专题
训练目标在数学上指定了模型应该如何从训练数据中学习和获取能力。训练基础模型的当前现状涉及特定于模型的目标。我们设想,未来基础模型的训练目标将反映两个变化:从系统证据和评估中得出的原则性选择,以及跨数据源和模式提供丰富、可扩展和…...

深入解析 Azure 机器学习平台:架构与组成部分
Azure机器学习平台是Microsoft Azure提供的一种云上机器学习服务,为开发者和数据科学家提供了一个全面且易于使用的环境来创建、训练、部署和管理机器学习模型。本文将对Azure机器学习平台的基本架构和组成部分进行深入解析,帮助读者全面了解该平台的工作…...

使用百度语音识别技术实现文字转语音的Java应用
探讨如何使用百度语音识别技术将文字转换为语音的Java应用。百度语音识别技术是一种强大的语音识别服务,可以将输入的文字转换为自然流畅的语音输出。我们将使用Java编程语言来实现这个应用,并提供相应的源代码。 首先,我们需要准备一些前提…...

【C#学习】文件操作
文章目录 常见操作拷贝文件检测文件夹是否存在并创建判断文件是否存在删除文件夹下的所有文件保留文件夹获取指定目录下的所有文件名删除 常见操作 拷贝文件 System.IO.File.Copy(sourcePath, targetPath); 检测文件夹是否存在并创建 //if directory not exit,then establis…...
Chrome版本对应Selenium版本
1.获得浏览器版本号和驱动 浏览器版本: 119.0.6045.124 浏览器驱动版本: 119.0.6043.1 / 120.0.6051.0 访问 https://vikyd.github.io/download-chromium-history-version/ 2. 安装selenium pip install selenium4.1.1 -i http://pypi.mirrors.ustc.edu.cn/simple/ --trusted…...
Day29力扣打卡
打卡记录 美丽塔 II(前后缀分解 单调栈) 链接 大佬的题解 class Solution:def maximumSumOfHeights(self, a: List[int]) -> int:n len(a)suf [0] * (n 1)st [n] # 哨兵s 0for i in range(n - 1, -1, -1):x a[i]while len(st) > 1 and …...

java源码用到的设计模式
Java 中有许多常用的设计模式,它们是为了解决特定问题而被反复使用和验证的经验总结。以下是一些常见的 Java 设计模式: 创建型模式 工厂模式 (Factory Pattern): 提供一个创建对象的接口,但是由子类决定实例化哪个类。例如:java…...

high perfermance computer usage
简单记一下hpc的使用: hpc就是一些科研机构或者大学建立的服务器中心。我这大学的每一位学生,可以轻松使用hpc批量跑数据,也可以新建自己的server跑一些local data,后者每个学生账号最大是32核512G的运行内存,体验非常…...
51单片机+DS1302设计一个电子钟(LCD1602显示时间)
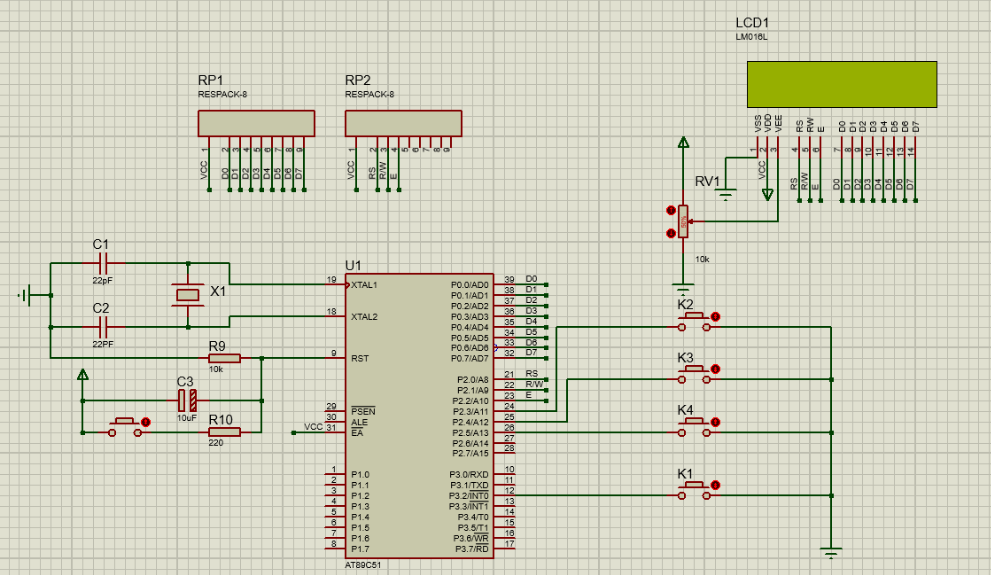
一、前言 电子钟是一种能够准确显示时间的设备,广泛应用于家庭、办公场所和公共场所,为人们提供了方便和准确的时间信息。本项目设计一个基于51单片机的电子钟,使用DS1302作为RTC时钟芯片,LCD1602作为显示屏,并通过串…...

vue项目中在scss代码中使用data中的变量
尽管在日常开发中,这类情况实际上很少出现。 VUE2: 在HTML中使用时,请确保将cssVars绑定在需要使用CSS变量的元素或该元素的上层元素上。 <template><div :style"cssVars"><div class"test"/></div><…...
uni-app报错“本应用使用HBuilderX x.x.x 或对应的cli版本编译,而手机端SDK版本是x.x.x不匹配的版本可能造成应用异常”
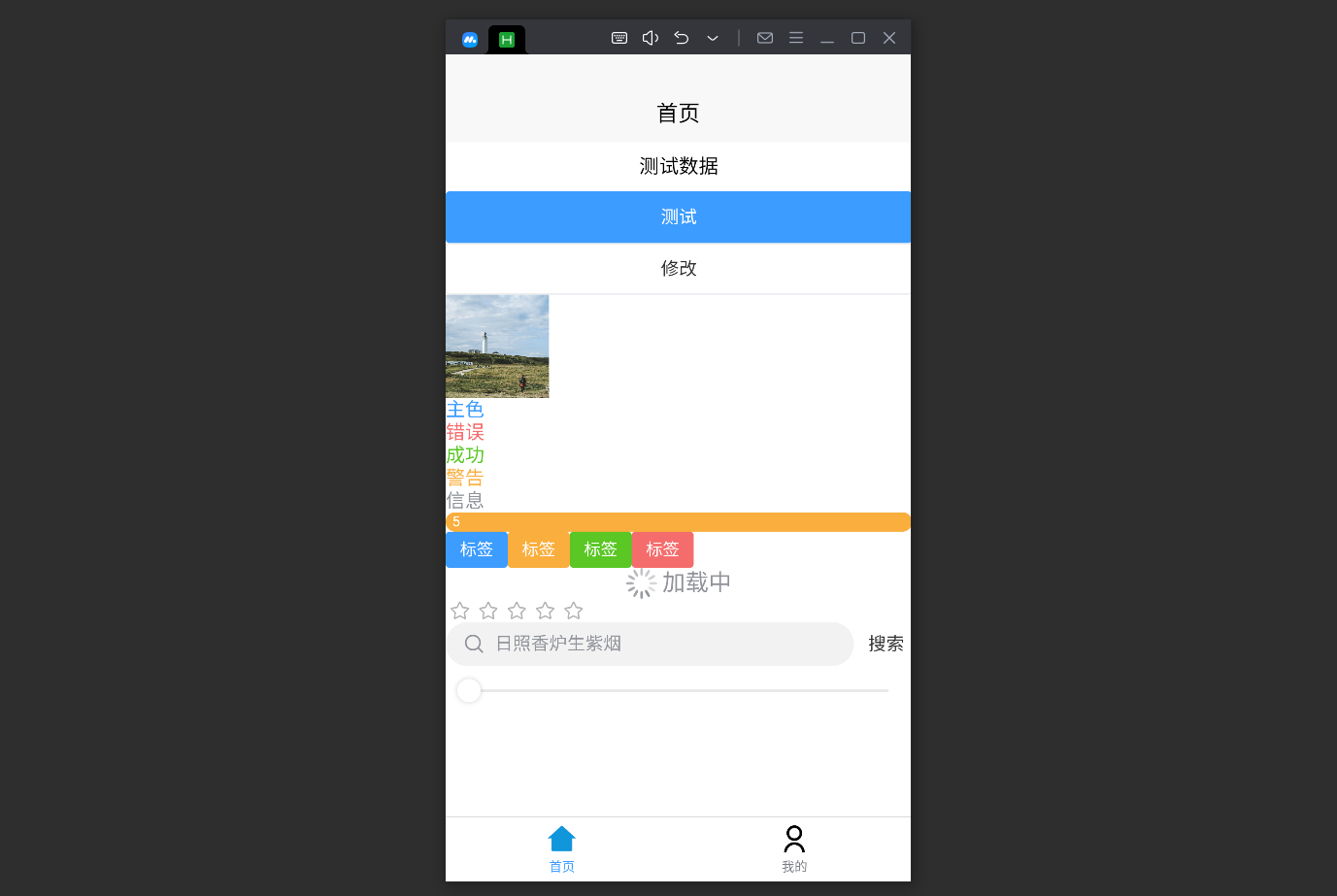
uniapp开发的一个跨平台软件,在安卓模拟器上启动的时候报警告: 官方给的解释:uni-app运行环境版本和编译器版本不一致的问题 - DCloud问答 解决办法有两个 方法一:添加忽略警告的配置 项目根目录下找到 manifest.json…...

[sd_scripts]之train
https://github.com/kohya-ss/sd-scripts/blob/main/docs/train_README-zh.mdhttps://github.com/kohya-ss/sd-scripts/blob/main/docs/train_README-zh.md 支持模型fine-tune,dreambooth,lora,textual inversion。 1.数据准备 在任意多个…...

samba 共享目录write permission deny问题修复 可读取内容但不可修改 删除 新增文件
关于 update/delete/write permission deny问题修复 0.首先在服务器端执行testparm -s ,测试 Samba 配置并显示结果。需确保服务器端参数 read only No ,共享目录有写入权限 一、若配置了允许匿名访问,使用匿名访问来操作smb需要做如下处理…...

UDP主要丢包原因及具体问题分析
一、主要丢包原因 1、接收端处理时间过长导致丢包:调用recv方法接收端收到数据后,处理数据花了一些时间,处理完后再次调用recv方法,在这二次调用间隔里,发过来的包可能丢失。对于这种情况可以修改接收端,将包接收后存入…...
647. 回文子串 516.最长回文子序列
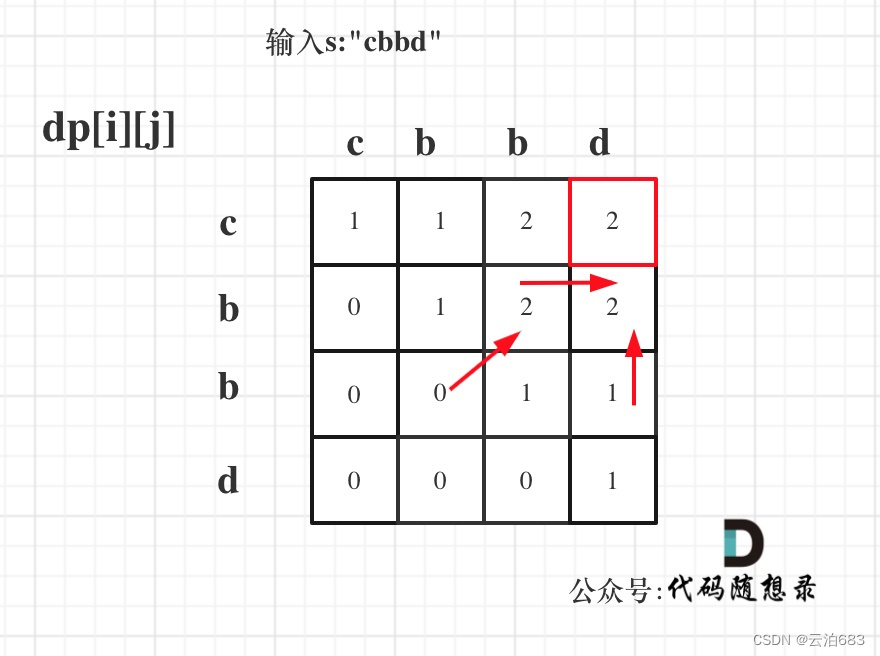
647. 回文子串 题目: 给你一个字符串 s ,请你统计并返回这个字符串中 回文子串 的数目。 回文字符串 是正着读和倒过来读一样的字符串。 子字符串 是字符串中的由连续字符组成的一个序列。 具有不同开始位置或结束位置的子串,即使是由相…...

点云从入门到精通技术详解100篇-双传感器模式的非结构化环境检测与识别
目录 前言 国内外研究现状 可通行区域检测的研究 障碍物检测的研究...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

调用支付宝接口响应40004 SYSTEM_ERROR问题排查
在对接支付宝API的时候,遇到了一些问题,记录一下排查过程。 Body:{"datadigital_fincloud_generalsaas_face_certify_initialize_response":{"msg":"Business Failed","code":"40004","sub_msg…...

Debian系统简介
目录 Debian系统介绍 Debian版本介绍 Debian软件源介绍 软件包管理工具dpkg dpkg核心指令详解 安装软件包 卸载软件包 查询软件包状态 验证软件包完整性 手动处理依赖关系 dpkg vs apt Debian系统介绍 Debian 和 Ubuntu 都是基于 Debian内核 的 Linux 发行版ÿ…...

2025 后端自学UNIAPP【项目实战:旅游项目】6、我的收藏页面
代码框架视图 1、先添加一个获取收藏景点的列表请求 【在文件my_api.js文件中添加】 // 引入公共的请求封装 import http from ./my_http.js// 登录接口(适配服务端返回 Token) export const login async (code, avatar) > {const res await http…...

自然语言处理——循环神经网络
自然语言处理——循环神经网络 循环神经网络应用到基于机器学习的自然语言处理任务序列到类别同步的序列到序列模式异步的序列到序列模式 参数学习和长程依赖问题基于门控的循环神经网络门控循环单元(GRU)长短期记忆神经网络(LSTM)…...
 自用)
css3笔记 (1) 自用
outline: none 用于移除元素获得焦点时默认的轮廓线 broder:0 用于移除边框 font-size:0 用于设置字体不显示 list-style: none 消除<li> 标签默认样式 margin: xx auto 版心居中 width:100% 通栏 vertical-align 作用于行内元素 / 表格单元格ÿ…...

如何在最短时间内提升打ctf(web)的水平?
刚刚刷完2遍 bugku 的 web 题,前来答题。 每个人对刷题理解是不同,有的人是看了writeup就等于刷了,有的人是收藏了writeup就等于刷了,有的人是跟着writeup做了一遍就等于刷了,还有的人是独立思考做了一遍就等于刷了。…...

OPenCV CUDA模块图像处理-----对图像执行 均值漂移滤波(Mean Shift Filtering)函数meanShiftFiltering()
操作系统:ubuntu22.04 OpenCV版本:OpenCV4.9 IDE:Visual Studio Code 编程语言:C11 算法描述 在 GPU 上对图像执行 均值漂移滤波(Mean Shift Filtering),用于图像分割或平滑处理。 该函数将输入图像中的…...

HarmonyOS运动开发:如何用mpchart绘制运动配速图表
##鸿蒙核心技术##运动开发##Sensor Service Kit(传感器服务)# 前言 在运动类应用中,运动数据的可视化是提升用户体验的重要环节。通过直观的图表展示运动过程中的关键数据,如配速、距离、卡路里消耗等,用户可以更清晰…...

Java数值运算常见陷阱与规避方法
整数除法中的舍入问题 问题现象 当开发者预期进行浮点除法却误用整数除法时,会出现小数部分被截断的情况。典型错误模式如下: void process(int value) {double half = value / 2; // 整数除法导致截断// 使用half变量 }此时...
