Unity中Shader矩阵的逆矩阵
文章目录
- 前言
- 一、逆矩阵的表示
- 二、逆矩阵的作用
- 四、逆矩阵的计算
- 五、顺序的重要性
- 六、矩阵的逆总结
- 1、求矩阵的逆前,这个矩阵必须得是个方阵
- 2、只有 A x A ^-1^ = A^-1^ x A = 1时,A的逆才是A^-1^
- 3、求2x2矩阵的逆:交换 a 和 b 的位置,把负数放在 b 和 c 的前面,然后用行列式(ad - bc)除以矩阵每个值
前言
Unity中Shader中用到的矩阵的逆矩阵
一、逆矩阵的表示
矩阵 A 的逆矩阵为 A-1
二、逆矩阵的作用
因为矩阵中没有除法。所以使用乘以矩阵的逆矩阵来代替矩阵除法
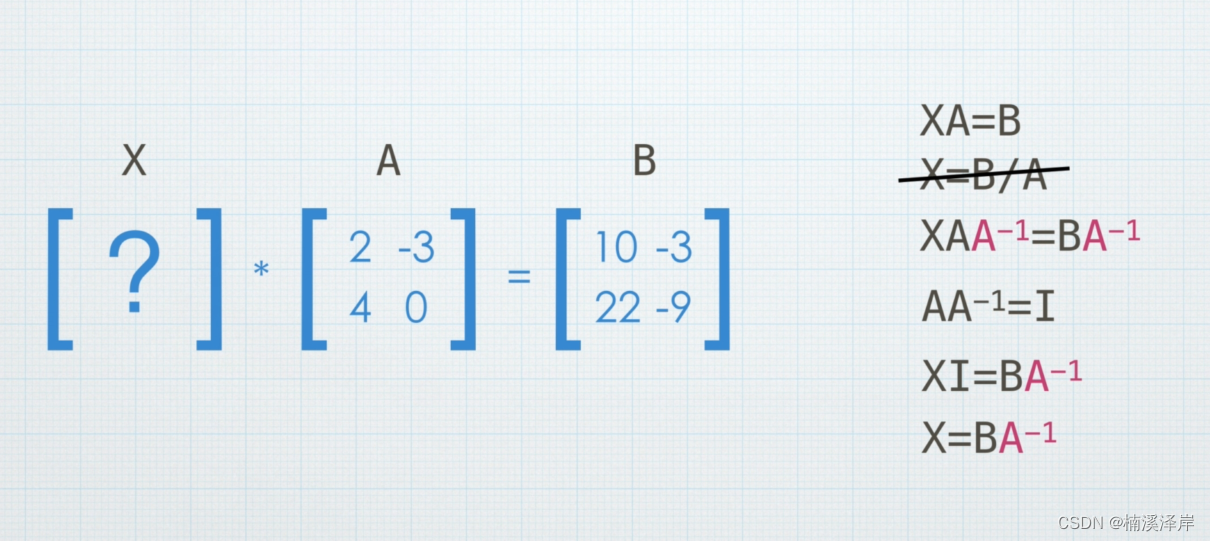
在上图中,我们要求出 X 矩阵,首先想到的是等式两边同时除以 A 矩阵
但是,矩阵中没有除法
所以,创造了逆矩阵用来乘
需要注意的是,矩阵乘法不符合乘法交换率。所以,乘的时候需要乘在需要消除的那一边
四、逆矩阵的计算
矩阵的逆矩阵需要计算到矩阵的行列式,所以逆矩阵的计算前提是矩阵是方阵
即 方阵 才有 逆矩阵
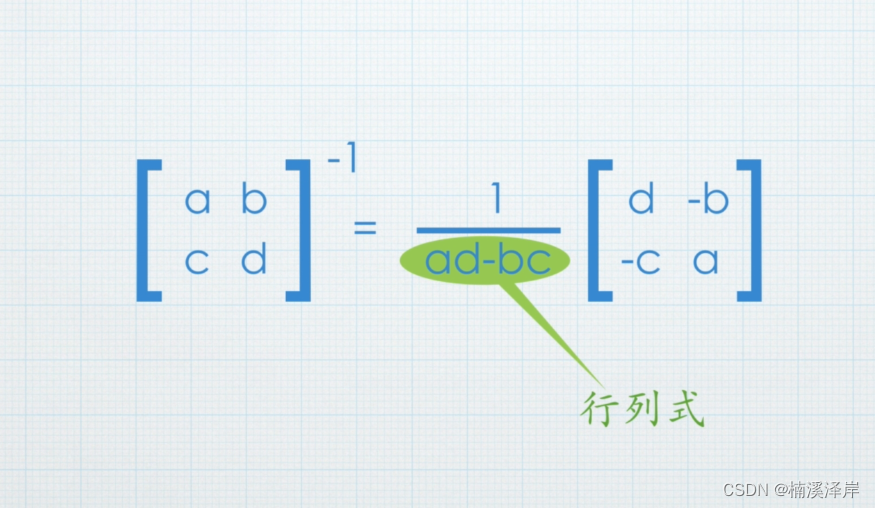
对于 2x2 方阵,行列式分之一右边的部分,左对角交换位置,右对角乘以-1
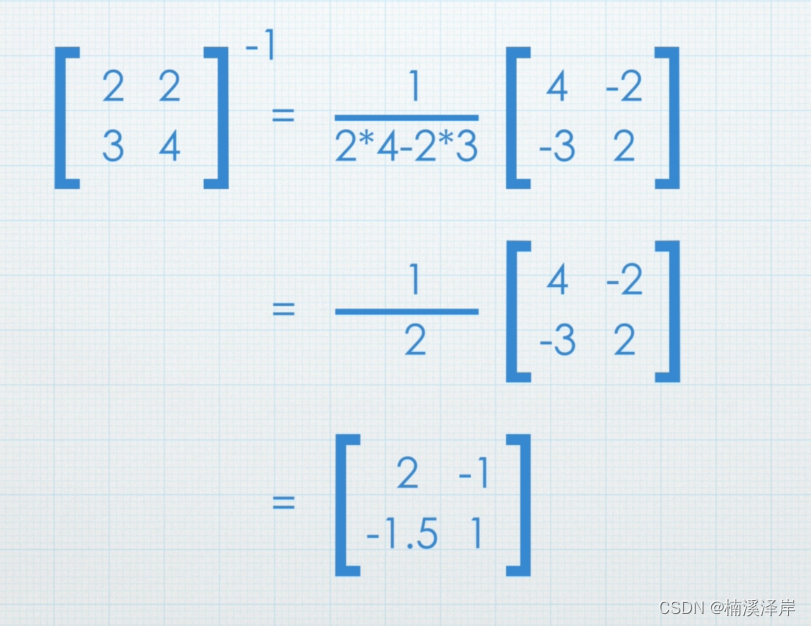
五、顺序的重要性
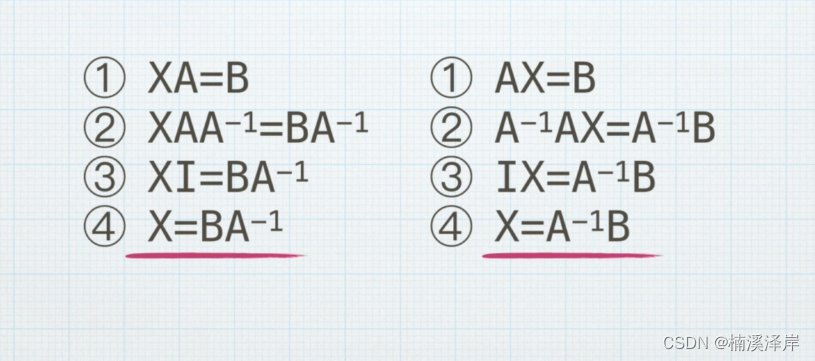
乘在左边 和 乘在右边 是完全不同的
六、矩阵的逆总结
1、求矩阵的逆前,这个矩阵必须得是个方阵
2、只有 A x A -1 = A-1 x A = 1时,A的逆才是A-1
3、求2x2矩阵的逆:交换 a 和 b 的位置,把负数放在 b 和 c 的前面,然后用行列式(ad - bc)除以矩阵每个值
相关文章:
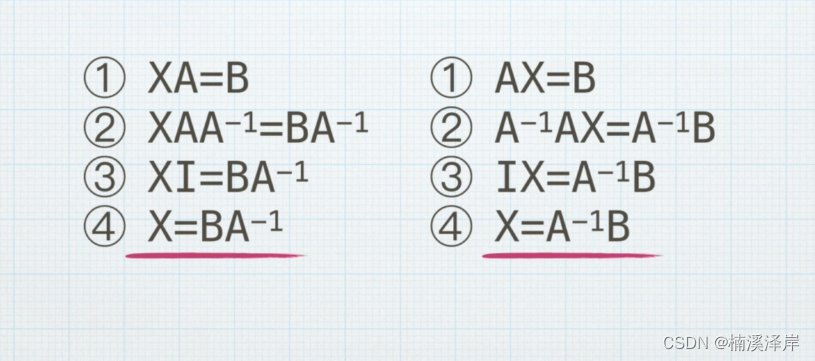
Unity中Shader矩阵的逆矩阵
文章目录 前言一、逆矩阵的表示二、逆矩阵的作用四、逆矩阵的计算五、顺序的重要性六、矩阵的逆总结1、求矩阵的逆前,这个矩阵必须得是个方阵2、只有 A x A ^-1^ A^-1^ x A 1时,A的逆才是A^-1^3、求2x2矩阵的逆:交换 a 和 b 的位置…...

我给网站做公安备案年度安全评估
我是卢松松,点点上面的头像,欢迎关注我哦! 差不多从2020年开始,我们的网站每年11月左右就要去公安备案做一次年度的安全评估,而现在又新增了APP和小程序备案。如下图所示: 评估的内容也很简单,…...
-通信中间件解析)
iceoryx(冰羚)-通信中间件解析
iceoryx(冰羚)-简介 iceoryx(冰羚)-Architecture iceoryx(冰羚)-Service Discovery iceoryx(冰羚)-examples-callbacks iceoryx(冰羚)-Listener设计 [iceoryx(冰羚)-ipc消息通信] [iceoryx(冰羚)-共享内存实现]...

Windows系统CMake+VS编译protobuf
目录 一些名词CMake构建VS工程下载protobuf源码下载CMake编译QT中使用 方案二失败:CMakeQT自带的Mingw编译参考链接 一些名词 lib dll lib库实际上分为两种,一种是静态链接lib库或者叫做静态lib库,另一种叫做动态链接库dll库的lib导入库或称…...
HarmonyOS开发(三):ArkTS基础
1、ArkTS演进 Mozilla创建了JS ---> Microsoft创建了TS ----> Huawei进一步推出ArkTS 从最初的基础逻辑交互(JS),到具备类型系统的高效工程开发(TS),再到融合声明式UI、多维状态管理等丰富的应用开发能力&…...

Java排序算法之堆排序
图解 堆排序是一种常见的排序算法,它借助了堆这种数据结构。堆是一种完全二叉树,它可以分为两种类型:最大堆和最小堆。在最大堆中,每个结点的值都大于等于它的子结点的值,而在最小堆中,每个结点的值都小于等…...
『GitHub项目圈选02』一款可实现视频自动翻译配音为其他语言的开源项目
🔥🔥🔥本周GitHub项目圈选****: 主要包含视频翻译、正则填字游戏、敏感词检测、聊天机器人框架、AI 换脸、分布式数据集成平台等热点项目。 1、pyvideotrans pyvideotrans 是一个视频翻译工具,可将一种语言的视频翻译为另一种语…...
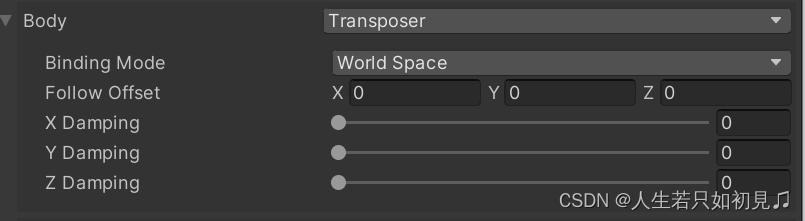
Unity - Cinemachine
动态获取Cinemachine的内部组件 vCam.GetCinemachineComponent<T>() 动态修改Cinemachine的Transposer属性 var vCamComp transfrom.GetComponent<CinemachineVirtualCamera>(); var transposerComp vCamComp.GetCinemachineComponent<CinemachineTransposer&…...

准备搞OpenStack了,先装一台最新的Ubuntu 23.10
正文共:1113 字 25 图,预估阅读时间:2 分钟 依稀记得前面发了一篇Ubuntu的安装文档(66%的经验丰富开发者和69%的学生更喜欢的Ubuntu的安装初体验),当时安装的是20.04.3的版本,现在看来已经是非常…...

Android 12 客制化修改初探-Launcher/Settings/Bootanimation
Android 12 使用 Material You 打造的全新系统界面,富有表现力、活力和个性。使用重新设计的微件、AppSearch、游戏模式和新的编解码器扩展您的应用。支持隐私信息中心和大致位置等新的保护功能。使用富媒体内容插入功能、更简便的模糊处理功能、经过改进的原生调试…...
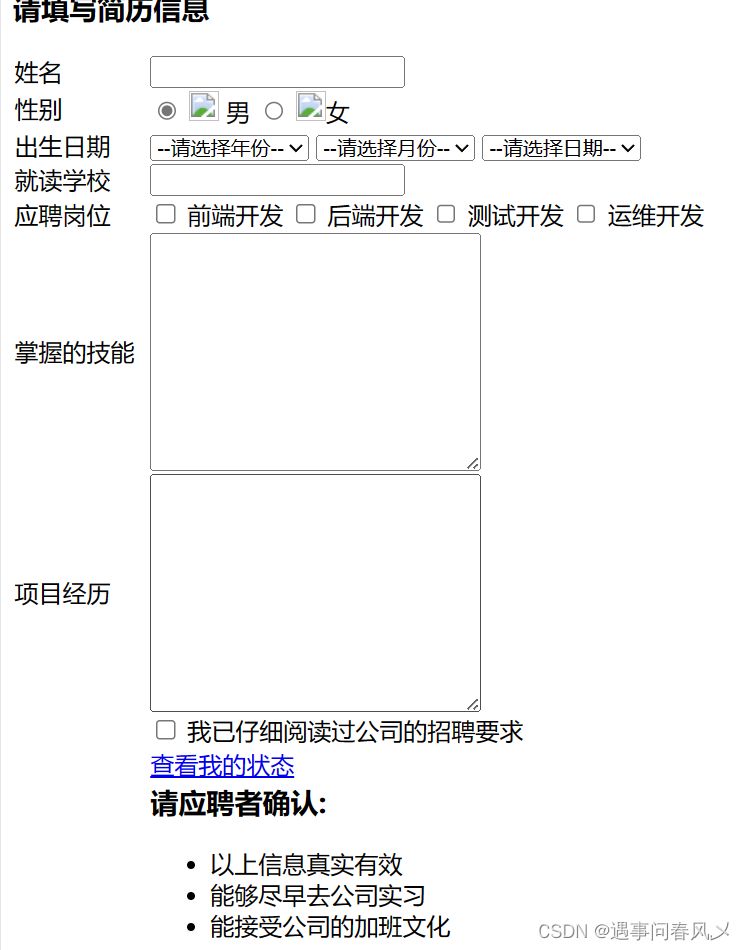
【JavaEE初阶】 HTML基础详解
文章目录 🎋什么是HTML?🍀HTML 结构🚩认识标签🚩HTML 文件基本结构🚩快速生成代码框架 🎄HTML 常见标签🚩注释标签🚩标题标签: h1-h6🚩段落标签: pǶ…...
C# Socket通信从入门到精通(10)——如何检测两台电脑之间的网络是否通畅
前言: 我们在完成了socket通信程序开发以后,并且IP地址也设置好以后,可以先通过一些手段来测试两台电脑之间的网络是否通畅,如果确认了网络通畅以后,我们再测试我们编写的Socket程序。 1、同时按下键盘的windows键+"R"键,如下图: 下面两张图是两种键盘的情…...
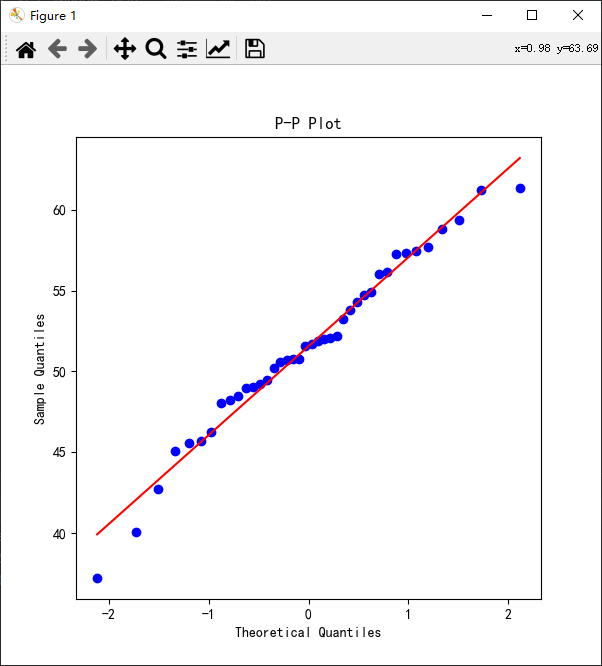
python科研绘图:P-P图与Q-Q图
目录 什么是P-P图与Q-Q图 分位数 百分位数 Q-Q图步骤与原理 Shapiro-Wilk检验 绘制Q-Q图 绘制P-P图 什么是P-P图与Q-Q图 P-P图和Q-Q图都是用于检验样本的概率分布是否服从某种理论分布。 P-P图的原理是检验实际累积概率分布与理论累积概率分布是否吻合。若吻合…...

浅尝:iOS的CoreGraphics和Flutter的Canvas
iOS的CoreGraphic 基本就是创建一个自定义的UIView,然后重写drawRect方法,在此方法里使用UIGraphicsGetCurrentContext()来绘制目标图形和样式 #import <UIKit/UIKit.h>interface MyGraphicView : UIView endimplementation MyGraphicView// Onl…...
网络安全黑客技术自学
前言 一、什么是网络安全 网络安全可以基于攻击和防御视角来分类,我们经常听到的 “红队”、“渗透测试” 等就是研究攻击技术,而“蓝队”、“安全运营”、“安全运维”则研究防御技术。 无论网络、Web、移动、桌面、云等哪个领域,都有攻与防…...
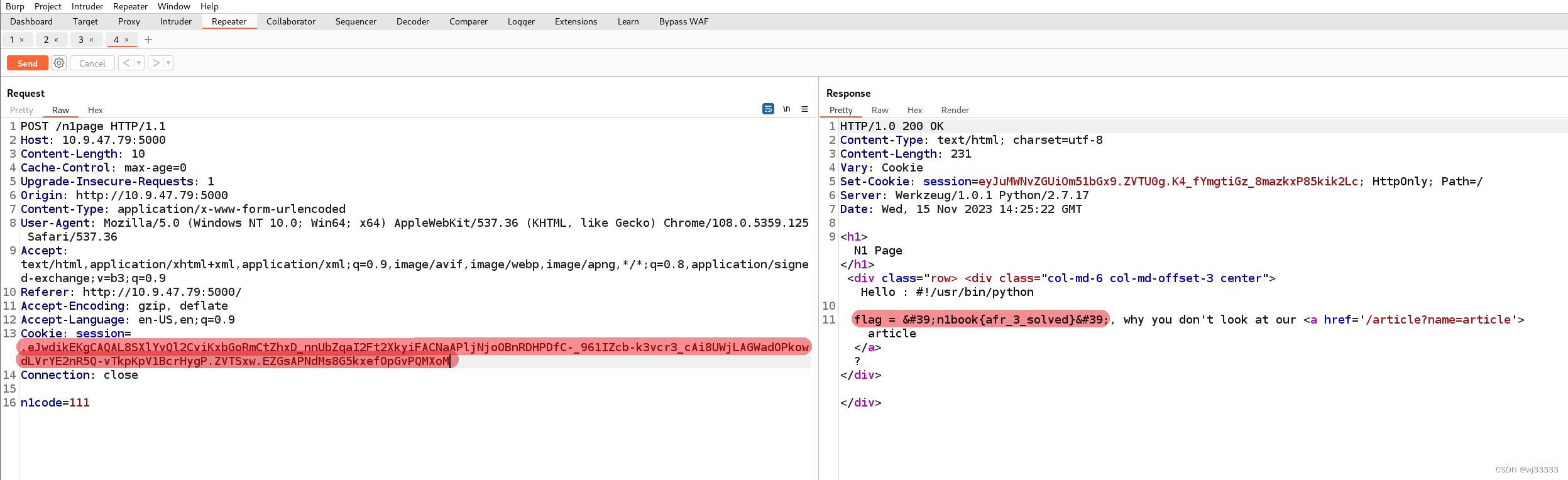
【文件读取/包含】任意文件读取漏洞 afr_3
1.1漏洞描述 漏洞名称任意文件读取漏洞 afr_3漏洞类型文件读取/包含漏洞等级⭐⭐⭐⭐⭐漏洞环境docker攻击方式 1.2漏洞等级 高危 1.3影响版本 暂无 1.4漏洞复现 1.4.1.基础环境 靶场docker工具BurpSuite 1.4.2.环境搭建 1.创建docker-compose.yml文件 version: 3.2 servi…...

第四章:单例模式与final
系列文章目录 文章目录 系列文章目录前言一、单例模式二、final 关键字总结 前言 单例模式与final关键字。 一、单例模式 设计模式是在大量的实践中总结和理论化之后优选的代码结构、编程风格、以及解决问题的思考方式。就像是经典的棋谱,不同的棋局,我…...
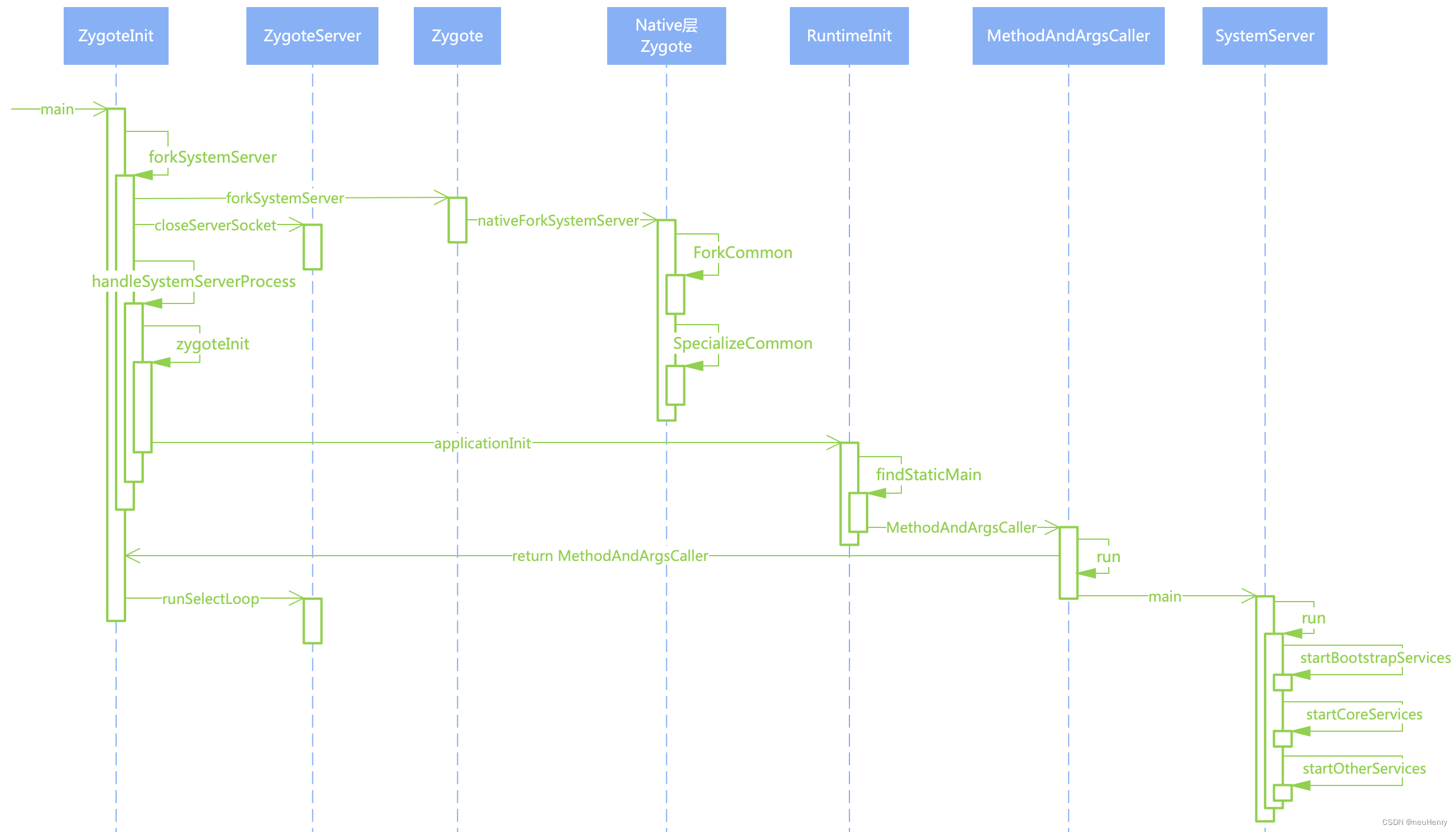
深入Android S(12.0) 探索 Android Framework 之 SystemServer 进程启动详解
深入学习 Android Framework 第三:深入Android S(12.0) 探索 Android Framework 之 SystemServer 进程启动详解 文章目录 深入学习 Android Framework前言一、Android 系统的启动流程1. 流程图2. 启动流程概述 二、源码详解1. 时序图2. 源代码1、ZygoteInit # main…...

搜维尔科技:【软件篇】TechViz是一款专为工程设计的专业级3D可视化软件
在沉浸式房间内深入研究您自己的 3D 数据 沉浸式房间是一个交互式虚拟现实空间,其中每个表面(墙壁、地板和天花板)都充当投影屏幕,创造高度沉浸式的体验。这就像您的 3D 模型有一个窗口,您可以在其中从不同角度走动、…...

android Handler
一、Handler的作用 1、Handler的作用是在andorid中实现线程间的通信。我们常说的说的,子线程处理逻辑,主线程更新UI是上述情况的一个子集。 二、源码分析 1、Handler源码 源码地址:http://androidxref.com/7.1.1_r6/xref/frameworks/base/co…...

srs linux
下载编译运行 git clone https:///ossrs/srs.git ./configure --h265on make 编译完成后即可启动SRS # 启动 ./objs/srs -c conf/srs.conf # 查看日志 tail -n 30 -f ./objs/srs.log 开放端口 默认RTMP接收推流端口是1935,SRS管理页面端口是8080,可…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

MySQL 8.0 OCP 英文题库解析(十三)
Oracle 为庆祝 MySQL 30 周年,截止到 2025.07.31 之前。所有人均可以免费考取原价245美元的MySQL OCP 认证。 从今天开始,将英文题库免费公布出来,并进行解析,帮助大家在一个月之内轻松通过OCP认证。 本期公布试题111~120 试题1…...

06 Deep learning神经网络编程基础 激活函数 --吴恩达
深度学习激活函数详解 一、核心作用 引入非线性:使神经网络可学习复杂模式控制输出范围:如Sigmoid将输出限制在(0,1)梯度传递:影响反向传播的稳定性二、常见类型及数学表达 Sigmoid σ ( x ) = 1 1 +...

深入理解Optional:处理空指针异常
1. 使用Optional处理可能为空的集合 在Java开发中,集合判空是一个常见但容易出错的场景。传统方式虽然可行,但存在一些潜在问题: // 传统判空方式 if (!CollectionUtils.isEmpty(userInfoList)) {for (UserInfo userInfo : userInfoList) {…...

windows系统MySQL安装文档
概览:本文讨论了MySQL的安装、使用过程中涉及的解压、配置、初始化、注册服务、启动、修改密码、登录、退出以及卸载等相关内容,为学习者提供全面的操作指导。关键要点包括: 解压 :下载完成后解压压缩包,得到MySQL 8.…...

Python网页自动化Selenium中文文档
1. 安装 1.1. 安装 Selenium Python bindings 提供了一个简单的API,让你使用Selenium WebDriver来编写功能/校验测试。 通过Selenium Python的API,你可以非常直观的使用Selenium WebDriver的所有功能。 Selenium Python bindings 使用非常简洁方便的A…...

算法—栈系列
一:删除字符串中的所有相邻重复项 class Solution { public:string removeDuplicates(string s) {stack<char> st;for(int i 0; i < s.size(); i){char target s[i];if(!st.empty() && target st.top())st.pop();elsest.push(s[i]);}string ret…...

【PX4飞控】mavros gps相关话题分析,经纬度海拔获取方法,卫星数锁定状态获取方法
使用 ROS1-Noetic 和 mavros v1.20.1, 携带经纬度海拔的话题主要有三个: /mavros/global_position/raw/fix/mavros/gpsstatus/gps1/raw/mavros/global_position/global 查看 mavros 源码,来分析他们的发布过程。发现前两个话题都对应了同一…...

使用 uv 工具快速部署并管理 vLLM 推理环境
uv:现代 Python 项目管理的高效助手 uv:Rust 驱动的 Python 包管理新时代 在部署大语言模型(LLM)推理服务时,vLLM 是一个备受关注的方案,具备高吞吐、低延迟和对 OpenAI API 的良好兼容性。为了提高部署效…...
