平衡树 - splay
相比于之前的普通平衡树进行左旋右旋来比,splay的适用性更高,使用更广泛。
核心函数rotate、splay函数,其它的根据需要进行修改。

int n, m;
struct Node {int s[2], p, v, cnt; // 左右儿子、父节点、值、出现数量int size, flag; // 子树大小、懒标记void init(int _v, int _p) { // 初始化函数v = _v, p = _p;cnt = size = 1;}
} tr[N];
int root, idx;// 根节点、分配节点序号void pushup(int u) { // 向上更新传递,与线段树一样 tr[u].size = tr[tr[u].s[0]].size + tr[tr[u].s[1]].size + tr[u].cnt;
}void pushdown(int x) { // 向下传递更新 ,与线段树一样if(tr[x].flag) {swap(tr[x].s[0], tr[x].s[1]);tr[tr[x].s[0]].flag ^= 1;tr[tr[x].s[1]].flag ^= 1;tr[x].flag = 0;}
}void rotate(int x) { // 核心函数 int y = tr[x].p, z = tr[y].p;int k = tr[y].s[1] == x;tr[z].s[tr[z].s[1] == y] = x, tr[x].p = z;tr[y].s[k] = tr[x].s[k ^ 1], tr[tr[x].s[k ^ 1]].p = y;tr[x].s[k ^ 1] = y, tr[y].p = x;pushup(y), pushup(x);
}void splay(int x, int k) { // 将x节点旋转到k节点下 while(tr[x].p != k) { // int y = tr[x].p; // x节点的父节点 int z = tr[y].p; // x节点的父节点的父节点 if(z != k) // 向上旋转 if((tr[y].s[1] == x) != (tr[z].s[1] == y)) rotate(x); // 转一次x else rotate(y); // 转一次y rotate(x); // 转一次x }if(!k) root = x; // 更新root节点
}void upper(int v) { // 将v值节点转到根节点 int u = root; // 根节点 while(tr[u].s[v > tr[u].v] && tr[u].v != v) // 存在则找到v值节点,不存在则找到v值节点的前驱或者后继节点 u = tr[u].s[v > tr[u].v]; // 向下寻找 splay(u, 0); // 将u节点旋转到跟节点
}int get_prev(int v) { // 获取v值的前驱节点 upper(v); // 将v值节点转到根节点 if(tr[root].v < v) return root; // 若是该值在树中不存在,根节点就是v的前驱或者后继节点 int u = tr[root].s[0]; // 前驱节点在左子树的最右边 while(tr[u].s[1]) u = tr[u].s[1]; // 找到最右边的一个节点 return u;
}int get_next(int v) { // 获取某值的后继节点 upper(v); // 将v值节点转到根节点if(tr[root].v > v) return root; // 若是该值在树中不存在,根节点就是v的前驱或者后继节点 int u = tr[root].s[1]; // 后继节点在右子树的最左边 while(tr[u].s[0]) u = tr[u].s[0]; // 找到最左的节点,就是最小的节点 return u; // 返回节点
}int get_rank_by_key(int v) { // key值在当前树中的排名 upper(v); // if(tr[root].v >= v)return tr[tr[root].s[0]].size + 1;return tr[tr[root].s[0]].size + tr[root].cnt + 1;
}int get_key_by_rank(int k) { // 获取树中排名为k的值 int u = root; // 根节点 while(tr[u].size >= k) { // 保证当前子树中有解 if(tr[tr[u].s[0]].size >= k) u = tr[u].s[0]; // 在左子树中 else if(tr[tr[u].s[0]].size + tr[u].cnt >= k) return splay(u, 0), tr[u].v; // 在当前节点 else k -= tr[tr[u].s[0]].size + tr[u].cnt, u = tr[u].s[1]; // 在右子树,需要更新k值,减去左子树以及当前节点值的数量 }return -1;
}void insert(int v) { // 在二叉树中插入一个值 int u = root, p = 0; // p维护为当前节点的父节点 while(u && tr[u].v != v) // 没找到则一直向下寻找 p = u, u = tr[u].s[v > tr[u].v]; // 更新父节点,更新当前节点 if(u) tr[u].cnt ++; // v值的节点已经存在则直接加一即可 else { // 不存在则创建节点 u = ++ idx; // 分配节点序号 if(p) tr[p].s[v > tr[p].v] = u; // 将父节点也就是前驱节点指向当前节点 tr[u].init(v, p); // 初始化当前节点的值、父节点信息 }splay(u, 0); // 将u节点旋转到根节点下
}void remove(int v) { // 删除一个值为v的节点 int prev = get_prev(v), nex = get_next(v); // 获取该节点的前驱以及后继节点。 splay(prev, 0), splay(nex, prev); // 将前继节点旋转到根节点,将后继节点旋转到前驱节点下面也就是根节点下面 int w = tr[nex].s[0]; // 后继节点的左子树就是v的节点 if(tr[w].cnt > 1) tr[w].cnt --, splay(w, 0); // 该节点的v不止存在一个,减一,w节点旋转到根节点 else tr[nex].s[0] = 0, splay(nex, 0); // 唯一,那么直接把后继节点的左子树指向空也就是0即可
}void output(int u) { // 中序遍历输出二叉树
// pushdown(u); int l = tr[u].s[0], r = tr[u].s[1]; // 左右儿子 if(l) output(l); // 递归左儿子 if(tr[u].v >= 1 && tr[u].v <= n) cout << tr[u].v << " "; // 输出当前子树的根 if(r) output(r); // 递归右儿子
}inline void sovle() {cin >> n;insert(-INF), insert(INF); // 插入两个哨兵,无穷小以及无穷大 使得在查询某数不存在的是时候不会产生越界while(n --) {int a, b;cin >> a >> b;if(a == 1) insert(b); // 插入一个值 if(a == 2) remove(b); // 插入一个值 if(a == 3) cout << get_rank_by_key(b) - 1 << endl; // 真实排名减一 因为前面多了一个哨兵 if(a == 4) cout << get_key_by_rank(b + 1) << endl; // 真实排名加一 因为哨兵 if(a == 5) cout << tr[get_prev(b)].v << endl; if(a == 6) cout << tr[get_next(b)].v << endl;}
}相关文章:

平衡树 - splay
相比于之前的普通平衡树进行左旋右旋来比,splay的适用性更高,使用更广泛。 核心函数rotate、splay函数,其它的根据需要进行修改。 int n, m; struct Node {int s[2], p, v, cnt; // 左右儿子、父节点、值、出现数量int size, flag; // 子树大…...

Spring Validation实践及其实现原理
Bean Validation 2.0 注解 校验空值 Null:验证对象是否为 null NotNull:验证对象是否不为 null NotEmpty:验证对象不为 null,且长度(数组、集合、字符串等)大于 0 NotBlank:验证字符串不为 nul…...
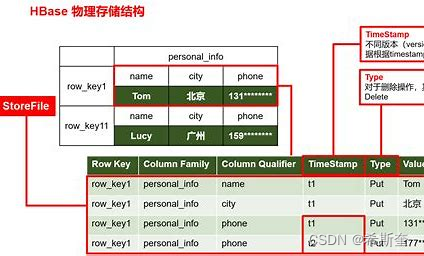
Java核心知识点整理大全18-笔记
Java核心知识点整理大全-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全2-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全3-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全4-笔记-CSDN博客 Java核心知识点整理大全5-笔记-CSDN博客 Java核心知识点整理大全6…...

vue 富文本编辑器多图上传
首先我使用的富文本编辑器是vue-quill-editor 使用npm进行下载 npm install vue-quill-editor --save当然也可以按照官方的方法下载,到官方 因为我是在原有老项目上开发的使用的组件库是ant-design-vue 1x版,当然使用其他组件库也可以 然后还有重要的一…...
)
简易地铁自动机售票系统实现(C++)
该程序具有以下功能 (1) 一个地铁路线类 Router,包含路线编号,途中的各个站点。可以新增、删除、查询路线,可以根据线路名称,显示线路图片。 (2) 一个地图类 Map,可以显示所有可以乘坐的地铁站名,以及线路…...
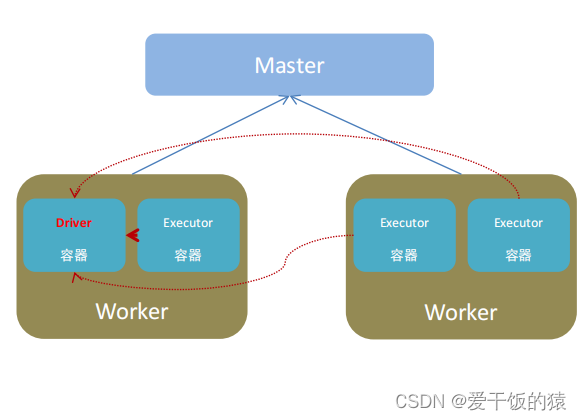
【Spark入门】基础入门
【大家好,我是爱干饭的猿,本文重点介绍Spark的定义、发展、扩展阅读:Spark VS Hadoop、四大特点、框架模块、运行模式、架构角色。 后续会继续分享其他重要知识点总结,如果喜欢这篇文章,点个赞👍ÿ…...

【自制开源】实时调参,手写字生成神器!大学生福音,告别繁琐的手写报告。
HandwritingGenerator HandwritingGenerator 是一个使用 PyQt6 制作的手写文本图片生成器。 该工具允许用户自定义多种效果,通过在左边配置效果参数,右边实时预览,并在调整好后输出图片。 效果预览 软件界面预览:一封情书&#x…...

Python 进阶(十一):高精度计算(decimal 模块)
《Python入门核心技术》专栏总目录・点这里 文章目录 1. 导入decimal模块2. 设置精度3. 创建Decimal对象4. 基本运算5. 比较运算6. 其他常用函数7. 注意事项8. 总结 大家好,我是水滴~~ 在进行数值计算时,浮点数的精度问题可能会导致结果的不准确性。为了…...

MCU常用文件格式
1. asm文件 asm是汇编语言源程序的扩展名,.asm文件是以asm作为扩展名的文件,是汇编语言的源程序文件。汇编语言(Assembly Language)是面向机器的程序设计语言,是利用计算机所有硬件特性并能直接控制硬件的语言。在汇编语言中,用助…...
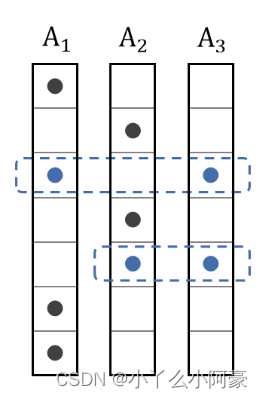
【机器学习】On the Identifiability of Nonlinear ICA: Sparsity and Beyond
前言 本文是对On the Identifiability of Nonlinear ICA: Sparsity and Beyond (NIPS 2022)中两个结构稀疏假设的总结。原文链接在Reference中。 什么是ICA(Independent component analysis)? 独立成分分析简单来说,就是给定很多的样本X,通…...
)
RBAC(Role-Based Access Control,基于角色的访问控制)
1. RBAC核心概念 RBAC(Role-Based Access Control,基于角色的访问控制)是一种广泛应用于软件和系统中的权限管理模型。它通过将用户与角色关联,再将角色与访问权限关联,来管理用户对系统资源的访问。RBAC模型的主要特…...

C++const指针的两种用法
const int *p &a; 指向const变量的指针 指向const变量的指针const修饰的变量,只能由指向const变量的指针去指向 p &a1;const的位置,必须在*的左边指向const变量的指针,可以被改变,可以指向别的变量可以指向普通变量&am…...

【Proteus仿真】【51单片机】智能垃圾桶设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真51单片机控制器,使用报警模块、LCD1602液晶模块、按键模块、人体红外传感器、HCSR04超声波、有害气体传感器、SG90舵机等。 主要功能: 系统运行后…...

【Windows】执行tasklist/taskkill提示“错误:找不到”或者“ERROR: not found”的解决方案
原因 由于WinMgmt异常导致起不来,而WinMgmt是SVCHOST进程中的WMI服务,解决这个问题需要停止之后再重新启动。 WinMgmt是Windows 2000客户端管理的核心组件,当客户端应用程序连接或当管理程序需要它本身的服务时,这个进程就会初始…...

MS2630——Sub-1 GHz、低噪声放大器芯片
产品简述 MS2630 是一款 Sub-1 GHz 低功耗、低噪声放大器 (LNA) 芯 片。芯片采用先进制造工艺,采用 SOT23-6 的封装形式。 主要特点 ◼ 典型噪声系数: 1.57dB ◼ 典型功率增益: 16.3dB ◼ 典型输出 P1dB : -9.2dBm…...

车载以太网-数据链路层-MAC
文章目录 车载以太网MAC(Media Access Control)车载以太网MAC帧格式以太网MAC帧报文示例车载以太网MAC层测试内容车载以太网MAC(Media Access Control) 车载以太网MAC(Media Access Control)是一种用于车载通信系统的以太网硬件地址,用于在物理层上识别和管理数据包的传…...

Tomcat源码分析
Tomcat源码分析与实例 Tomcat是一个开源的Java Web服务器,它提供了一种简单的方式来部署和运行Java Web应用程序。本文将详细介绍Tomcat的源码分析和实例。 1. Tomcat源码分析 1.1 目录结构 Tomcat的源码目录结构如下: tomcat-x.y.z/ ├── bin/ ├…...
计算机视觉面试题-02
图像处理和计算机视觉基础 什么是图像滤波?有哪些常见的图像滤波器? 图像滤波是一种通过在图像上应用滤波器(卷积核)来改变图像外观或提取图像特征的图像处理技术。滤波器通常是一个小的矩阵,通过在图像上进行卷积…...
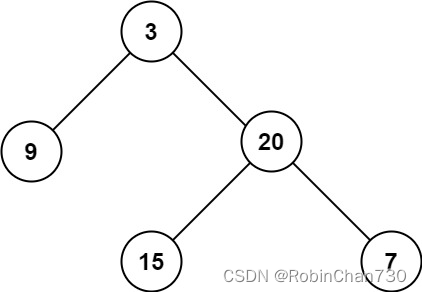
力扣日记11.27-【二叉树篇】二叉树的最大深度
力扣日记:【二叉树篇】二叉树的最大深度 日期:2023.11.27 参考:代码随想录、力扣 104. 二叉树的最大深度 题目描述 难度: 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最…...
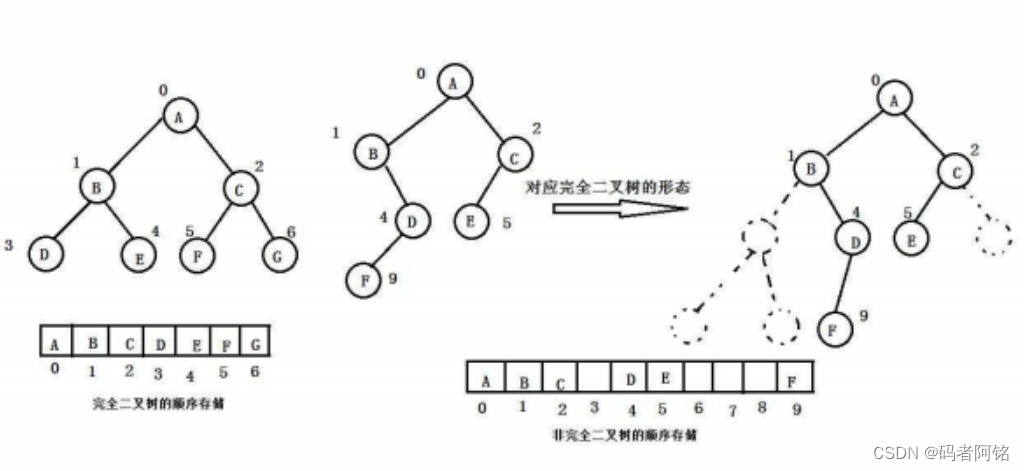
【数据结构】树的概念以及二叉树
目录 1 树概念及结构 1.1 树的概念 1.3 树的存储 2 二叉树的概念及结构 2.1 概念 2.2 特殊的二叉树 2.3 二叉树的性质 2.4 二叉树的存储结构 1 树概念及结构 1.1 树的概念 树是一种非线性的数据结构,它是由n(n>0)个有限结点组…...

PPT|230页| 制造集团企业供应链端到端的数字化解决方案:从需求到结算的全链路业务闭环构建
制造业采购供应链管理是企业运营的核心环节,供应链协同管理在供应链上下游企业之间建立紧密的合作关系,通过信息共享、资源整合、业务协同等方式,实现供应链的全面管理和优化,提高供应链的效率和透明度,降低供应链的成…...

Neo4j 集群管理:原理、技术与最佳实践深度解析
Neo4j 的集群技术是其企业级高可用性、可扩展性和容错能力的核心。通过深入分析官方文档,本文将系统阐述其集群管理的核心原理、关键技术、实用技巧和行业最佳实践。 Neo4j 的 Causal Clustering 架构提供了一个强大而灵活的基石,用于构建高可用、可扩展且一致的图数据库服务…...

【python异步多线程】异步多线程爬虫代码示例
claude生成的python多线程、异步代码示例,模拟20个网页的爬取,每个网页假设要0.5-2秒完成。 代码 Python多线程爬虫教程 核心概念 多线程:允许程序同时执行多个任务,提高IO密集型任务(如网络请求)的效率…...

Java多线程实现之Thread类深度解析
Java多线程实现之Thread类深度解析 一、多线程基础概念1.1 什么是线程1.2 多线程的优势1.3 Java多线程模型 二、Thread类的基本结构与构造函数2.1 Thread类的继承关系2.2 构造函数 三、创建和启动线程3.1 继承Thread类创建线程3.2 实现Runnable接口创建线程 四、Thread类的核心…...

Device Mapper 机制
Device Mapper 机制详解 Device Mapper(简称 DM)是 Linux 内核中的一套通用块设备映射框架,为 LVM、加密磁盘、RAID 等提供底层支持。本文将详细介绍 Device Mapper 的原理、实现、内核配置、常用工具、操作测试流程,并配以详细的…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

云原生安全实战:API网关Kong的鉴权与限流详解
🔥「炎码工坊」技术弹药已装填! 点击关注 → 解锁工业级干货【工具实测|项目避坑|源码燃烧指南】 一、基础概念 1. API网关(API Gateway) API网关是微服务架构中的核心组件,负责统一管理所有API的流量入口。它像一座…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

【学习笔记】erase 删除顺序迭代器后迭代器失效的解决方案
目录 使用 erase 返回值继续迭代使用索引进行遍历 我们知道类似 vector 的顺序迭代器被删除后,迭代器会失效,因为顺序迭代器在内存中是连续存储的,元素删除后,后续元素会前移。 但一些场景中,我们又需要在执行删除操作…...

Visual Studio Code 扩展
Visual Studio Code 扩展 change-case 大小写转换EmmyLua for VSCode 调试插件Bookmarks 书签 change-case 大小写转换 https://marketplace.visualstudio.com/items?itemNamewmaurer.change-case 选中单词后,命令 changeCase.commands 可预览转换效果 EmmyLua…...
