二叉树题目:结点与其祖先之间的最大差值
文章目录
- 题目
- 标题和出处
- 难度
- 题目描述
- 要求
- 示例
- 数据范围
- 解法一
- 思路和算法
- 代码
- 复杂度分析
- 解法二
- 思路和算法
- 代码
- 复杂度分析
题目
标题和出处
标题:结点与其祖先之间的最大差值
出处:1026. 结点与其祖先之间的最大差值
难度
5 级
题目描述
要求
给定二叉树的根结点 root \texttt{root} root,找出存在于不同结点 a \texttt{a} a 和 b \texttt{b} b 之间的最大值 v \texttt{v} v,其中 v = |a.val - b.val| \texttt{v = |a.val - b.val|} v = |a.val - b.val|,且 a \texttt{a} a 是 b \texttt{b} b 的祖先。
如果 a \texttt{a} a 的任何子结点是 b \texttt{b} b,或者 a \texttt{a} a 的任何子结点是 b \texttt{b} b 的祖先,那么 a \texttt{a} a 是 b \texttt{b} b 的祖先。
示例
示例 1:
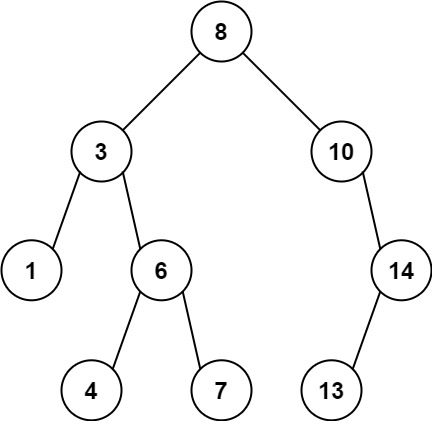
输入: root = [8,3,10,1,6,null,14,null,null,4,7,13] \texttt{root = [8,3,10,1,6,null,14,null,null,4,7,13]} root = [8,3,10,1,6,null,14,null,null,4,7,13]
输出: 7 \texttt{7} 7
解释:
我们有若干结点与其祖先的差值,其中一些如下:
|8 - 3| = 5 \texttt{|8 - 3| = 5} |8 - 3| = 5
|3 - 7| = 4 \texttt{|3 - 7| = 4} |3 - 7| = 4
|8 - 1| = 7 \texttt{|8 - 1| = 7} |8 - 1| = 7
|10 - 13| = 3 \texttt{|10 - 13| = 3} |10 - 13| = 3
在所有可能的差值中,最大值 7 \texttt{7} 7 由 |8 - 1| = 7 \texttt{|8 - 1| = 7} |8 - 1| = 7 得出。
示例 2:

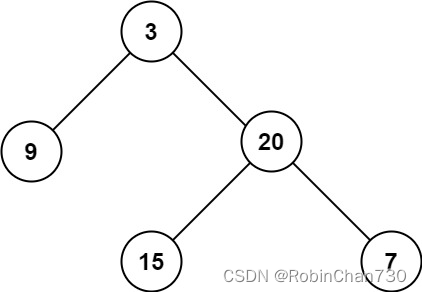
输入: root = [1,null,2,null,0,3] \texttt{root = [1,null,2,null,0,3]} root = [1,null,2,null,0,3]
输出: 3 \texttt{3} 3
数据范围
- 树中结点数目在范围 [2, 5000] \texttt{[2, 5000]} [2, 5000] 内
- 0 ≤ Node.val ≤ 10 5 \texttt{0} \le \texttt{Node.val} \le \texttt{10}^\texttt{5} 0≤Node.val≤105
解法一
思路和算法
二叉树中的每个结点对应一条从根结点到该结点的路径,路径存在最大结点值和最小结点值。对于每个结点,该结点与其祖先之间的最大差值可能是以下两种情况之一:
-
路径上的最大结点值与当前结点值之差;
-
当前结点值与路径上的最小结点值之差。
可以使用深度优先搜索计算二叉树中的每个结点与其祖先之间的最大差值。从根结点开始遍历全部结点,由于同一条路径上的结点的遍历顺序是从上到下,在访问到一个结点时,该结点的所有祖先结点都已经被访问过,因此可以得到从根结点到该结点的路径上的最大结点值和最小结点值,计算当前结点与其祖先之间的最大差值。
在访问一个结点之后,对于其非空子结点,更新从根结点到子结点的路径上的最大结点值和最小结点值,对子结点继续遍历。
遍历结束之后,即可得到二叉树中结点与祖先之间的最大差值。
题目要求计算差值的两个结点应满足两个结点不同且一个结点是另一个结点的祖先。上述做法虽然没有考虑计算差值的两个结点是否相同,但是也能得到正确的结果,理由如下。
由于给定的二叉树的结点数目至少为 2 2 2,因此一定存在两个不同的结点且这两个结点之间存在祖先和后代的关系。任何一个结点与其自身的差值一定是 0 0 0。对于两个不同的结点,如果结点值相同则差值等于 0 0 0,如果结点值不同则差值大于 0 0 0,即差值一定不会小于 0 0 0,因此一定存在两个不同的结点,这两个结点之间存在祖先和后代的关系且这两个结点值之差的绝对值等于最大差值。
代码
class Solution {int maxDiff = 0;public int maxAncestorDiff(TreeNode root) {dfs(root, root.val, root.val);return maxDiff;}public void dfs(TreeNode node, int maxValue, int minValue) {int currDiff = Math.max(maxValue - node.val, node.val - minValue);maxDiff = Math.max(maxDiff, currDiff);TreeNode left = node.left, right = node.right;if (left != null) {int leftMaxValue = Math.max(left.val, maxValue);int leftMinValue = Math.min(left.val, minValue);dfs(left, leftMaxValue, leftMinValue);}if (right != null) {int rightMaxValue = Math.max(right.val, maxValue);int rightMinValue = Math.min(right.val, minValue);dfs(right, rightMaxValue, rightMinValue);}}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是栈空间,取决于二叉树的高度,最坏情况下二叉树的高度是 O ( n ) O(n) O(n)。
解法二
思路和算法
也可以使用广度优先搜索计算二叉树中结点与祖先之间的最大差值。从根结点开始遍历全部结点,访问结点的顺序为层数递增的顺序,遍历过程中,对于每个结点,得到该结点对应的从根结点到该结点的路径上的最大结点值和最小结点值,计算该结点与其祖先之间的最大差值。
为了记录每个结点对应的从根结点到该结点的路径上的最大结点值和最小结点值,需要使用三个队列,分别存储结点、路径上的最大结点值和路径上的最小结点值,这三个队列分别为结点队列、最大值队列和最小值队列,初始时将根结点入结点队列,将根结点值入最大值队列和最小值队列。每次将一个结点、一个最大值和一个最小值分别从结点队列、最大值队列和最小值队列出队列,计算当前结点与其祖先之间的最大差值。对于当前结点的非空子结点,计算从根结点到子结点的路径上的最大结点值和最小结点值,然后将子结点以及子结点对应的最大结点值和最小结点值分别入结点队列、最大值队列和最小值队列。
遍历结束之后,即可得到二叉树中结点与祖先之间的最大差值。
代码
class Solution {public int maxAncestorDiff(TreeNode root) {int maxDiff = 0;Queue<TreeNode> nodeQueue = new ArrayDeque<TreeNode>();Queue<Integer> maxNode = new ArrayDeque<Integer>();Queue<Integer> minNode = new ArrayDeque<Integer>();nodeQueue.offer(root);maxNode.offer(root.val);minNode.offer(root.val);while (!nodeQueue.isEmpty()) {TreeNode node = nodeQueue.poll();int maxValue = maxNode.poll();int minValue = minNode.poll();int currDiff = Math.max(maxValue - node.val, node.val - minValue);maxDiff = Math.max(maxDiff, currDiff);TreeNode left = node.left, right = node.right;if (left != null) {nodeQueue.offer(left);maxNode.offer(Math.max(left.val, maxValue));minNode.offer(Math.min(left.val, minValue));}if (right != null) {nodeQueue.offer(right);maxNode.offer(Math.max(right.val, maxValue));minNode.offer(Math.min(right.val, minValue));}}return maxDiff;}
}
复杂度分析
-
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。每个结点都被访问一次。
-
空间复杂度: O ( n ) O(n) O(n),其中 n n n 是二叉树的结点数。空间复杂度主要是队列空间,队列内元素个数不超过 n n n。
相关文章:

二叉树题目:结点与其祖先之间的最大差值
文章目录 题目标题和出处难度题目描述要求示例数据范围 解法一思路和算法代码复杂度分析 解法二思路和算法代码复杂度分析 题目 标题和出处 标题:结点与其祖先之间的最大差值 出处:1026. 结点与其祖先之间的最大差值 难度 5 级 题目描述 要求 给…...

平衡树 - splay
相比于之前的普通平衡树进行左旋右旋来比,splay的适用性更高,使用更广泛。 核心函数rotate、splay函数,其它的根据需要进行修改。 int n, m; struct Node {int s[2], p, v, cnt; // 左右儿子、父节点、值、出现数量int size, flag; // 子树大…...

Spring Validation实践及其实现原理
Bean Validation 2.0 注解 校验空值 Null:验证对象是否为 null NotNull:验证对象是否不为 null NotEmpty:验证对象不为 null,且长度(数组、集合、字符串等)大于 0 NotBlank:验证字符串不为 nul…...
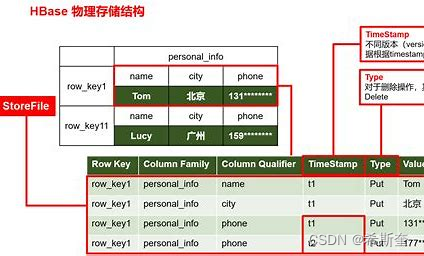
Java核心知识点整理大全18-笔记
Java核心知识点整理大全-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全2-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全3-笔记_希斯奎的博客-CSDN博客 Java核心知识点整理大全4-笔记-CSDN博客 Java核心知识点整理大全5-笔记-CSDN博客 Java核心知识点整理大全6…...

vue 富文本编辑器多图上传
首先我使用的富文本编辑器是vue-quill-editor 使用npm进行下载 npm install vue-quill-editor --save当然也可以按照官方的方法下载,到官方 因为我是在原有老项目上开发的使用的组件库是ant-design-vue 1x版,当然使用其他组件库也可以 然后还有重要的一…...
)
简易地铁自动机售票系统实现(C++)
该程序具有以下功能 (1) 一个地铁路线类 Router,包含路线编号,途中的各个站点。可以新增、删除、查询路线,可以根据线路名称,显示线路图片。 (2) 一个地图类 Map,可以显示所有可以乘坐的地铁站名,以及线路…...
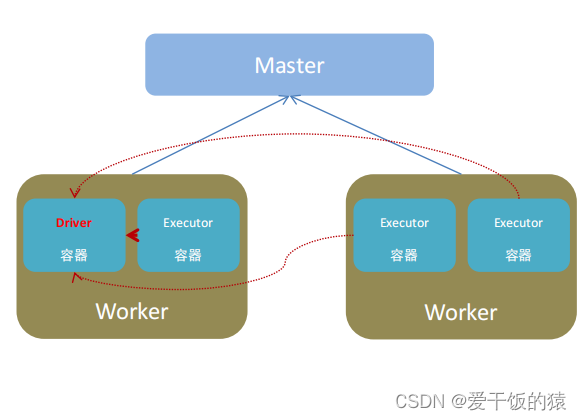
【Spark入门】基础入门
【大家好,我是爱干饭的猿,本文重点介绍Spark的定义、发展、扩展阅读:Spark VS Hadoop、四大特点、框架模块、运行模式、架构角色。 后续会继续分享其他重要知识点总结,如果喜欢这篇文章,点个赞👍ÿ…...

【自制开源】实时调参,手写字生成神器!大学生福音,告别繁琐的手写报告。
HandwritingGenerator HandwritingGenerator 是一个使用 PyQt6 制作的手写文本图片生成器。 该工具允许用户自定义多种效果,通过在左边配置效果参数,右边实时预览,并在调整好后输出图片。 效果预览 软件界面预览:一封情书&#x…...

Python 进阶(十一):高精度计算(decimal 模块)
《Python入门核心技术》专栏总目录・点这里 文章目录 1. 导入decimal模块2. 设置精度3. 创建Decimal对象4. 基本运算5. 比较运算6. 其他常用函数7. 注意事项8. 总结 大家好,我是水滴~~ 在进行数值计算时,浮点数的精度问题可能会导致结果的不准确性。为了…...

MCU常用文件格式
1. asm文件 asm是汇编语言源程序的扩展名,.asm文件是以asm作为扩展名的文件,是汇编语言的源程序文件。汇编语言(Assembly Language)是面向机器的程序设计语言,是利用计算机所有硬件特性并能直接控制硬件的语言。在汇编语言中,用助…...
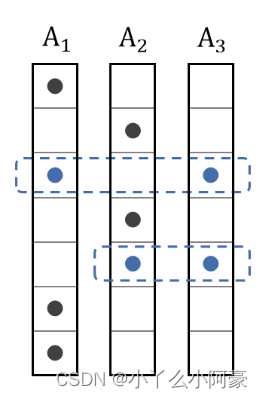
【机器学习】On the Identifiability of Nonlinear ICA: Sparsity and Beyond
前言 本文是对On the Identifiability of Nonlinear ICA: Sparsity and Beyond (NIPS 2022)中两个结构稀疏假设的总结。原文链接在Reference中。 什么是ICA(Independent component analysis)? 独立成分分析简单来说,就是给定很多的样本X,通…...
)
RBAC(Role-Based Access Control,基于角色的访问控制)
1. RBAC核心概念 RBAC(Role-Based Access Control,基于角色的访问控制)是一种广泛应用于软件和系统中的权限管理模型。它通过将用户与角色关联,再将角色与访问权限关联,来管理用户对系统资源的访问。RBAC模型的主要特…...

C++const指针的两种用法
const int *p &a; 指向const变量的指针 指向const变量的指针const修饰的变量,只能由指向const变量的指针去指向 p &a1;const的位置,必须在*的左边指向const变量的指针,可以被改变,可以指向别的变量可以指向普通变量&am…...

【Proteus仿真】【51单片机】智能垃圾桶设计
文章目录 一、功能简介二、软件设计三、实验现象联系作者 一、功能简介 本项目使用Proteus8仿真51单片机控制器,使用报警模块、LCD1602液晶模块、按键模块、人体红外传感器、HCSR04超声波、有害气体传感器、SG90舵机等。 主要功能: 系统运行后…...

【Windows】执行tasklist/taskkill提示“错误:找不到”或者“ERROR: not found”的解决方案
原因 由于WinMgmt异常导致起不来,而WinMgmt是SVCHOST进程中的WMI服务,解决这个问题需要停止之后再重新启动。 WinMgmt是Windows 2000客户端管理的核心组件,当客户端应用程序连接或当管理程序需要它本身的服务时,这个进程就会初始…...

MS2630——Sub-1 GHz、低噪声放大器芯片
产品简述 MS2630 是一款 Sub-1 GHz 低功耗、低噪声放大器 (LNA) 芯 片。芯片采用先进制造工艺,采用 SOT23-6 的封装形式。 主要特点 ◼ 典型噪声系数: 1.57dB ◼ 典型功率增益: 16.3dB ◼ 典型输出 P1dB : -9.2dBm…...

车载以太网-数据链路层-MAC
文章目录 车载以太网MAC(Media Access Control)车载以太网MAC帧格式以太网MAC帧报文示例车载以太网MAC层测试内容车载以太网MAC(Media Access Control) 车载以太网MAC(Media Access Control)是一种用于车载通信系统的以太网硬件地址,用于在物理层上识别和管理数据包的传…...

Tomcat源码分析
Tomcat源码分析与实例 Tomcat是一个开源的Java Web服务器,它提供了一种简单的方式来部署和运行Java Web应用程序。本文将详细介绍Tomcat的源码分析和实例。 1. Tomcat源码分析 1.1 目录结构 Tomcat的源码目录结构如下: tomcat-x.y.z/ ├── bin/ ├…...
计算机视觉面试题-02
图像处理和计算机视觉基础 什么是图像滤波?有哪些常见的图像滤波器? 图像滤波是一种通过在图像上应用滤波器(卷积核)来改变图像外观或提取图像特征的图像处理技术。滤波器通常是一个小的矩阵,通过在图像上进行卷积…...
力扣日记11.27-【二叉树篇】二叉树的最大深度
力扣日记:【二叉树篇】二叉树的最大深度 日期:2023.11.27 参考:代码随想录、力扣 104. 二叉树的最大深度 题目描述 难度: 给定一个二叉树 root ,返回其最大深度。 二叉树的 最大深度 是指从根节点到最远叶子节点的最…...

新能源汽车智慧充电桩管理方案:新能源充电桩散热问题及消防安全监管方案
随着新能源汽车的快速普及,充电桩作为核心配套设施,其安全性与可靠性备受关注。然而,在高温、高负荷运行环境下,充电桩的散热问题与消防安全隐患日益凸显,成为制约行业发展的关键瓶颈。 如何通过智慧化管理手段优化散…...

STM32HAL库USART源代码解析及应用
STM32HAL库USART源代码解析 前言STM32CubeIDE配置串口USART和UART的选择使用模式参数设置GPIO配置DMA配置中断配置硬件流控制使能生成代码解析和使用方法串口初始化__UART_HandleTypeDef结构体浅析HAL库代码实际使用方法使用轮询方式发送使用轮询方式接收使用中断方式发送使用中…...

jmeter聚合报告中参数详解
sample、average、min、max、90%line、95%line,99%line、Error错误率、吞吐量Thoughput、KB/sec每秒传输的数据量 sample(样本数) 表示测试中发送的请求数量,即测试执行了多少次请求。 单位,以个或者次数表示。 示例:…...

Ubuntu系统复制(U盘-电脑硬盘)
所需环境 电脑自带硬盘:1块 (1T) U盘1:Ubuntu系统引导盘(用于“U盘2”复制到“电脑自带硬盘”) U盘2:Ubuntu系统盘(1T,用于被复制) !!!建议“电脑…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

MySQL的pymysql操作
本章是MySQL的最后一章,MySQL到此完结,下一站Hadoop!!! 这章很简单,完整代码在最后,详细讲解之前python课程里面也有,感兴趣的可以往前找一下 一、查询操作 我们需要打开pycharm …...

【深度学习新浪潮】什么是credit assignment problem?
Credit Assignment Problem(信用分配问题) 是机器学习,尤其是强化学习(RL)中的核心挑战之一,指的是如何将最终的奖励或惩罚准确地分配给导致该结果的各个中间动作或决策。在序列决策任务中,智能体执行一系列动作后获得一个最终奖励,但每个动作对最终结果的贡献程度往往…...

leetcode73-矩阵置零
leetcode 73 思路 记录 0 元素的位置:遍历整个矩阵,找出所有值为 0 的元素,并将它们的坐标记录在数组zeroPosition中置零操作:遍历记录的所有 0 元素位置,将每个位置对应的行和列的所有元素置为 0 具体步骤 初始化…...

【大模型】RankRAG:基于大模型的上下文排序与检索增强生成的统一框架
文章目录 A 论文出处B 背景B.1 背景介绍B.2 问题提出B.3 创新点 C 模型结构C.1 指令微调阶段C.2 排名与生成的总和指令微调阶段C.3 RankRAG推理:检索-重排-生成 D 实验设计E 个人总结 A 论文出处 论文题目:RankRAG:Unifying Context Ranking…...

C++ 类基础:封装、继承、多态与多线程模板实现
前言 C 是一门强大的面向对象编程语言,而类(Class)作为其核心特性之一,是理解和使用 C 的关键。本文将深入探讨 C 类的基本特性,包括封装、继承和多态,同时讨论类中的权限控制,并展示如何使用类…...
