leetcode 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
采用dp[i] 表示含有i个节点的二叉搜索树,其中二叉搜索树由左子树和右子树以及根结点组成。其中dp[i]由含有i-j节点的左子树和j-1节点的右子树和一个根结点组成。所以dp[i]的构造形式由左右子树决定。
最优子结构 dp[i]
状态转移方程:dp[i] += (dp[i - j] * dp[j - 1])
int numTrees(int n) {int dp[20] = {0};dp[0] = 1;dp[1] = 1;for (int i = 2; i <= n; ++i) {for (int j = 1; j <= i; ++j) {dp[i] += (dp[i - j] * dp[j - 1]);}}return dp[n];
}
相关文章:

leetcode 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 示例 1: 输入:n 3 输出:5 示例 2: 输入:n 1 输出:…...
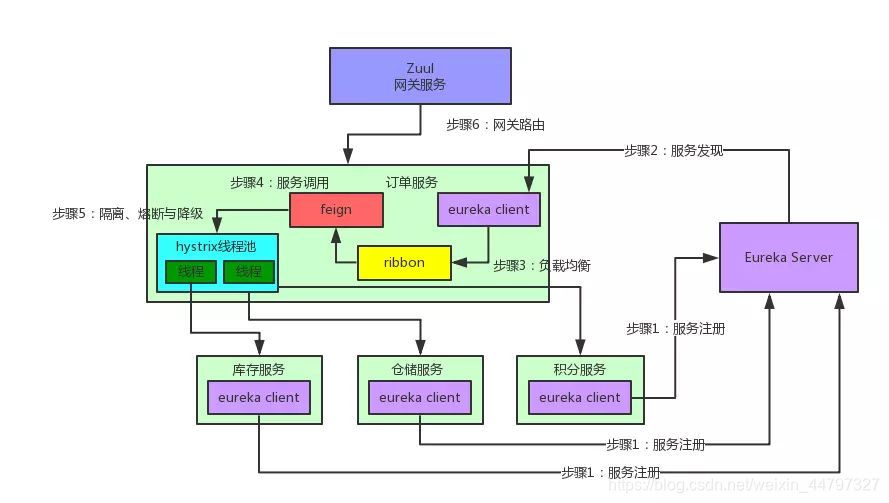
通俗易懂的spring Cloud;业务场景介绍 二、Spring Cloud核心组件:Eureka 、Feign、Ribbon、Hystrix、zuul
文章目录 通俗易懂的spring Cloud一、业务场景介绍二、Spring Cloud核心组件:Eureka三、Spring Cloud核心组件:Feign四、Spring Cloud核心组件:Ribbon五、Spring Cloud核心组件:Hystrix六、Spring Cloud核心组件:Zuul七…...

大数据预处理技术
文章目录 前言 大数据技术成为前沿专业 也是现在甚至未来的朝阳产业,大数据有分别是 数据预处理 数据存储 大数据处理和分析 数据可视化 部分组成 ,大数据行业有数据则称王,大数据的核心是数据本身 怎么获取有价值的数据呢?本章讲…...

跳表的学习记录
跳表(Skip List)是一种数据结构,它通过在多个层次上添加额外的前向指针来提高有序数据的搜索效率。跳表与其他常见的有序数据结构(如二叉搜索树、平衡树如AVL树和红黑树、B树等)相比,具有其独特的优缺点&am…...

电子学会C/C++编程等级考试2022年09月(二级)真题解析
C/C++等级考试(1~8级)全部真题・点这里 第1题:统计误差范围内的数 统计一个整数序列中与指定数字m误差范围小于等于X的数的个数。 时间限制:5000 内存限制:65536输入 输入包含三行: 第一行为N,表示整数序列的长度(N <= 100); 第二行为N个整数,整数之间以一个空格分…...
如何使用nginx部署静态资源
Nginx可以作为静态web服务器来部署静态资源,这个静态资源是指在服务端真实存在,并且能够直接展示的一些文件数据,比如常见的静态资源有html页面、css文件、js文件、图片、视频、音频等资源相对于Tomcat服务器来说,Nginx处理静态资…...
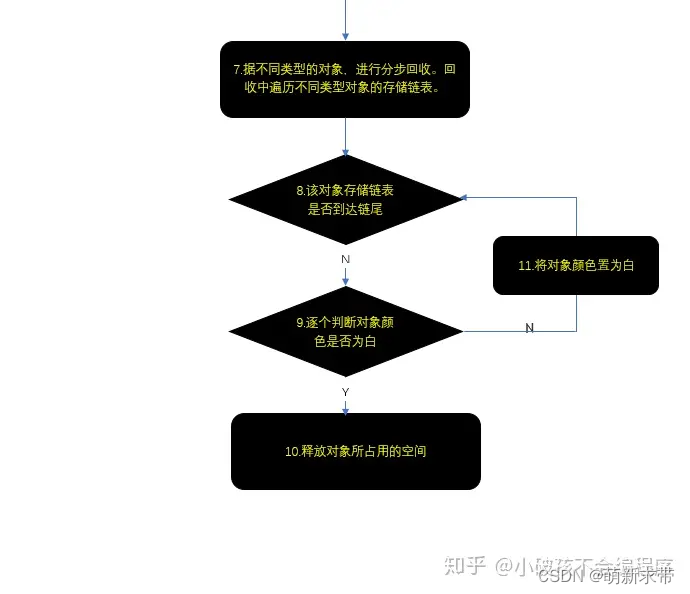
lua的gc原理
lua垃圾回收(Garbage Collect)是lua中一个比较重要的部分。由于lua源码版本变迁,目前大多数有关这个方面的文章都还是基于lua5.1版本,有一定的滞后性。因此本文通过参考当前的5.3.4版本的Lua源码,希望对Lua的GC算法有一个较为详尽的探讨。 L…...

redis作为缓存详解
目录 前言: 为什么说关系型数据库性能不高 如何提高MySQL并发量 缓存更新策略 定期更新 实时更新 内存淘汰策略 Redis内置的淘汰策略 缓存常见问题 缓存预热 缓存穿透 缓存雪崩 缓存击穿 前言: 对于缓存的理解,缓存目的就是为了…...
231127 刷题日报
这周值班。。多少写道题吧,保持每天的手感。老婆给买了lubuladong纸质书,加油卷。 1. 131. 分割回文串 写个这个吧,钉在耻辱柱上的题。 为啥没写出来: 1. 递归树没画对 把树枝只看做是1个字母,而且不清楚树枝和节点…...
【Linux】vim-多模式的文本编辑器
本篇文章内容和干货较多,希望对大家有所帮助👍 目录 一、vim的介绍 1.1 vi 与 vim的概念1.2 Vim 和 Vi 的一些对比 二、vim 模式之间的切换 2.1 进入vim2.2 [正常模式]切换到[插入模式]2.3 [插入模式]切换至[正常模式]2.4 [正常模式]切换至[底行模式…...

Ubuntu 启用 root 用户
在启用 root 用户之前,我们先来了解一下, ubuntu 命令的组成。 打开 ubuntu 的终端,现在的命令行是由 topeetubuntu:~$ 这几个字母组成,那么这几个字母都代表 什么意思呢? topeet …...
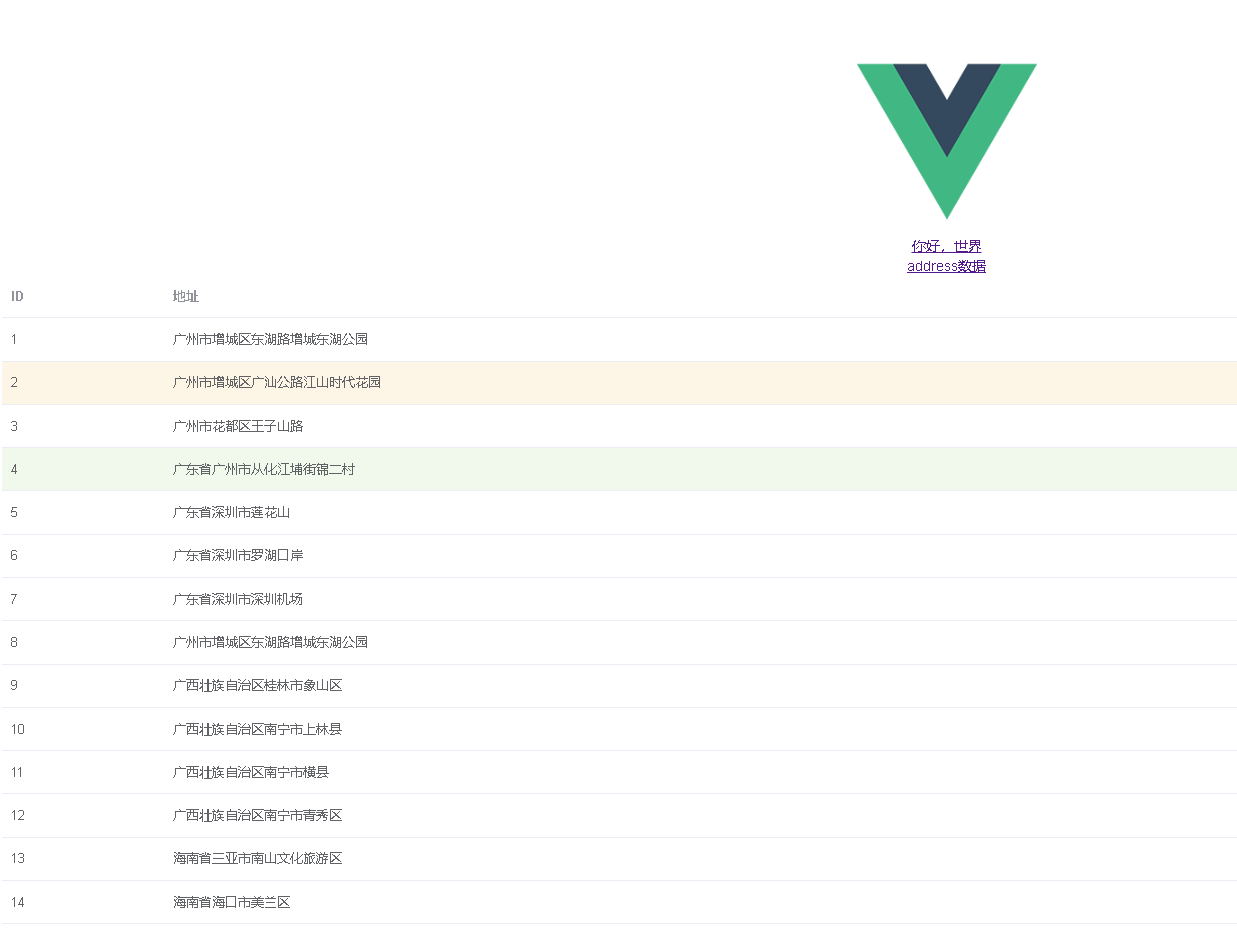
手摸手Element-ui路由VueRoute
后端WebAPI准备 https://router.vuejs.org/zh/guide/ https://v3.router.vuejs.org/zh/installation.html <template><el-table:data"tableData"style"width: 100%":row-class-name"tableRowClassName"><!-- <el-table-colum…...

探究Kafka原理-5.Kafka设计原理和生产者原理解析
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码、Kafka原理🔥如果感觉博主的文章还不错的话,请ὄ…...

浅谈C#在unity应用中的工厂模式
文章目录 前言简单工厂模式工厂方法模式抽象工厂模式Unity实战 前言 工厂模式是一种创建型设计模式,它提供了一种将对象的实例化过程封装起来的方法,使得客户端代码不必直接依赖于具体类。这有助于降低代码的耦合度,提高代码的可维护性和可扩…...

卷积神经网络(Inception-ResNet-v2)交通标志识别
文章目录 一、前言二、前期工作1. 设置GPU(如果使用的是CPU可以忽略这步)2. 导入数据3. 查看数据 二、构建一个tf.data.Dataset1.加载数据2. 配置数据集 三、构建Inception-ResNet-v2网络1.自己搭建2.官方模型 五、设置动态学习率六、训练模型七、模型评…...

网易云音频数据如何爬取?
在当今数字化时代,音频数据的获取和处理变得越来越重要。本文将详细介绍如何使用Objective-C语言构建音频爬虫程序,以爬取网易云音乐为案例。我们将从Objective-C的基础知识开始,逐步深入到爬取思路分析、构建爬虫框架、完整爬取代码等方面&a…...

97、Text2NeRF: Text-Driven 3D Scene Generation with Neural Radiance Fields
简介 论文地址 使用扩散模型来推断文本相关图像作为内容先验,并使用单目深度估计方法来提供几何先验,并引入了一种渐进的场景绘制和更新策略,保证不同视图之间纹理和几何的一致性 实现流程 简单而言: 文本-图片扩散模型生成一…...
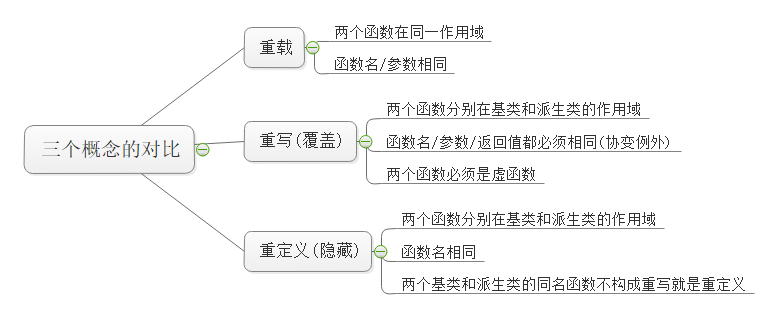
【C++】多态(上) 多态 | 虚函数 | 重写 | final、override | 接口继承与实现继承 | 抽象类
一、多态 概念 多态,就是多种状态,即不同的对象去完成同一个行为时会产生出不同的状态。比如:买票时,成人要原价买,学生和老人就可以享受优惠价便宜一点儿。同样是买票这个行为,不同的对象来做就有不同的…...

国内怎么投资黄金,炒黄金有哪些好方法?
随着我国综合实力的不断强大,投资市场的发展也日臻完善,现已成为了国际黄金市场的重要组成部分,人们想要精准判断金市走向,就离不开对我国经济等信息的仔细分析。而想要有效提升盈利概率,人们还需要掌握国内黄金投资的…...
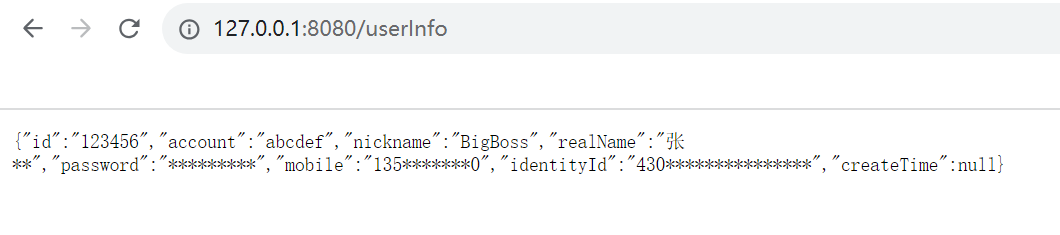
springboot实现数据脱敏
springboot实现数据脱敏 怎么说呢,写着写着发觉 ”这写的什么玩意“ 。 总的来说就是,这篇文章并不能解决数据脱敏问题,但以下链接可以。 SpringBoot中利用自定义注解优雅地实现隐私数据脱敏 然后回到本文,本来是想基于AOP代理&am…...
详解)
后进先出(LIFO)详解
LIFO 是 Last In, First Out 的缩写,中文译为后进先出。这是一种数据结构的工作原则,类似于一摞盘子或一叠书本: 最后放进去的元素最先出来 -想象往筒状容器里放盘子: (1)你放进的最后一个盘子(…...

React 第五十五节 Router 中 useAsyncError的使用详解
前言 useAsyncError 是 React Router v6.4 引入的一个钩子,用于处理异步操作(如数据加载)中的错误。下面我将详细解释其用途并提供代码示例。 一、useAsyncError 用途 处理异步错误:捕获在 loader 或 action 中发生的异步错误替…...

【Linux】shell脚本忽略错误继续执行
在 shell 脚本中,可以使用 set -e 命令来设置脚本在遇到错误时退出执行。如果你希望脚本忽略错误并继续执行,可以在脚本开头添加 set e 命令来取消该设置。 举例1 #!/bin/bash# 取消 set -e 的设置 set e# 执行命令,并忽略错误 rm somefile…...

在鸿蒙HarmonyOS 5中实现抖音风格的点赞功能
下面我将详细介绍如何使用HarmonyOS SDK在HarmonyOS 5中实现类似抖音的点赞功能,包括动画效果、数据同步和交互优化。 1. 基础点赞功能实现 1.1 创建数据模型 // VideoModel.ets export class VideoModel {id: string "";title: string ""…...

连锁超市冷库节能解决方案:如何实现超市降本增效
在连锁超市冷库运营中,高能耗、设备损耗快、人工管理低效等问题长期困扰企业。御控冷库节能解决方案通过智能控制化霜、按需化霜、实时监控、故障诊断、自动预警、远程控制开关六大核心技术,实现年省电费15%-60%,且不改动原有装备、安装快捷、…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Spring Boot面试题精选汇总
🤟致敬读者 🟩感谢阅读🟦笑口常开🟪生日快乐⬛早点睡觉 📘博主相关 🟧博主信息🟨博客首页🟫专栏推荐🟥活动信息 文章目录 Spring Boot面试题精选汇总⚙️ **一、核心概…...

JUC笔记(上)-复习 涉及死锁 volatile synchronized CAS 原子操作
一、上下文切换 即使单核CPU也可以进行多线程执行代码,CPU会给每个线程分配CPU时间片来实现这个机制。时间片非常短,所以CPU会不断地切换线程执行,从而让我们感觉多个线程是同时执行的。时间片一般是十几毫秒(ms)。通过时间片分配算法执行。…...

零基础在实践中学习网络安全-皮卡丘靶场(第九期-Unsafe Fileupload模块)(yakit方式)
本期内容并不是很难,相信大家会学的很愉快,当然对于有后端基础的朋友来说,本期内容更加容易了解,当然没有基础的也别担心,本期内容会详细解释有关内容 本期用到的软件:yakit(因为经过之前好多期…...

Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习)
Aspose.PDF 限制绕过方案:Java 字节码技术实战分享(仅供学习) 一、Aspose.PDF 简介二、说明(⚠️仅供学习与研究使用)三、技术流程总览四、准备工作1. 下载 Jar 包2. Maven 项目依赖配置 五、字节码修改实现代码&#…...
