智能优化算法应用:基于蜻蜓算法无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于蜻蜓算法无线传感器网络(WSN)覆盖优化 - 附代码
文章目录
- 智能优化算法应用:基于蜻蜓算法无线传感器网络(WSN)覆盖优化 - 附代码
- 1.无线传感网络节点模型
- 2.覆盖数学模型及分析
- 3.蜻蜓算法
- 4.实验参数设定
- 5.算法结果
- 6.参考文献
- 7.MATLAB代码
摘要:本文主要介绍如何用蜻蜓算法进行无线传感器网(WSN)覆盖优化。
1.无线传感网络节点模型
本文主要基于0/1模型,进行寻优。在二维平面上传感器节点的感知范围是一个以节点为圆心,半径为 R n R_n Rn的圆形区域,该圆形区域通常被称为该节点的“感知圆盘”, R n R_n Rn称为传感器节点的感知半径,感知半径与节点内置传感器件的物理特性有关,假设节点 n n n的位置坐标为 ( x n , y n ) (x_n,y_n) (xn,yn)在0-1感知模型中,对于平面上任意一点 p ( x p , y p ) p(x_p,y_p) p(xp,yp),则节点 n n n监测到区域内点 p p p的事件发生概率为:
P r ( n , p ) = { 1 , d ( n , p ) ≤ R n 0 , e s l e (1) P_r(n,p)=\begin{cases}1, \,d(n,p)\leq R_n\\ 0,\, esle \end{cases}\tag{1} Pr(n,p)={1,d(n,p)≤Rn0,esle(1)
其中 d ( n , p ) = ( x n − x p ) 2 + ( y n − y p ) 2 d(n,p)=\sqrt{(x_n-x_p)^2+(y_n-y_p)^2} d(n,p)=(xn−xp)2+(yn−yp)2为点和之间的欧式距离。
2.覆盖数学模型及分析
现假定目标监测区域为二维平面,在区域 A r e a Area Area上投放同型结构传感器节点的数目为N,每个节点的位置坐标值假设已被初始化赋值,且节点的感知半径r。传感器节点集则表示为:
N o d e { x 1 , . . . , x N } (2) Node\{x_1,...,x_N\} \tag{2} Node{x1,...,xN}(2)
其中 n o d e i = { x i , y i , r } node_i=\{x_i,y_i,r\} nodei={xi,yi,r},表示以节点 ( x i , y i ) (x_i,y_i) (xi,yi)为圆心,r为监测半径的圆,假定监测区域 A r e a Area Area被数字化离散为 m ∗ n m*n m∗n个像素点,像素点的坐标为 ( x , y ) (x,y) (x,y),目标像素点与传感器节点间的距离为:
d ( n o d e i , p ) = ( x i − x ) 2 + ( y i − y ) 2 (3) d(node_i,p)=\sqrt{(x_i-x)^2+(y_i-y)^2}\tag{3} d(nodei,p)=(xi−x)2+(yi−y)2(3)
目标区域内像素点被传感器节点所覆盖的事件定义为 c i c_i ci。则该事件发生的概率 P c i P{c_i} Pci即为像素点 ( x , y ) (x,y) (x,y)被传感器节点 n o d e i node_i nodei所覆盖的概率:
P c o v ( x , y , n o d e i ) = { 1 , i f d ( n o d e i , p ) ≤ r 0 , e s l e (4) P_{cov}(x,y,node_i)=\begin{cases}1, if\,d(node_i,p)\leq r\\ 0,\, esle \end{cases}\tag{4} Pcov(x,y,nodei)={1,ifd(nodei,p)≤r0,esle(4)
我们将所有的传感器节点在目标监测环境中的区域覆盖率 C o v e r R a t i o CoverRatio CoverRatio定义为传感器节点集的覆盖面积与监测区域的面积之比,如公式所示:
C o v e r R a t i o = ∑ P c o v m ∗ n (5) CoverRatio = \frac{\sum P_{cov}}{m*n}\tag{5} CoverRatio=m∗n∑Pcov(5)
那我们的最终目标就是找到一组节点使得覆盖率最大。
3.蜻蜓算法
蜻蜓算法原理请参考:https://blog.csdn.net/u011835903/article/details/107783363
该算法是寻找最小值。于是适应度函数定义为未覆盖率最小,即覆盖率最大。如下:
f u n = a r g m i n ( 1 − C o v e r R a t i o ) = a r g m i n ( 1 − ∑ P c o v m ∗ n ) (6) fun = argmin(1 - CoverRatio) = argmin(1-\frac{\sum P_{cov}}{m*n}) \tag{6} fun=argmin(1−CoverRatio)=argmin(1−m∗n∑Pcov)(6)
4.实验参数设定
无线传感器覆盖参数设定如下:
%% 设定WNS覆盖参数,
%% 默认输入参数都是整数,如果想定义小数,请自行乘以系数变为整数再做转换。
%% 比如范围1*1,R=0.03可以转换为100*100,R=3;
%区域范围为AreaX*AreaY
AreaX = 100;
AreaY = 100;
N = 20 ;%覆盖节点数
R = 15;%通信半径蜻蜓算法参数如下:
%% 设定优化参数
pop=30; % 种群数量
Max_iteration=80; %设定最大迭代次数
lb = ones(1,2*N);
ub = [AreaX.*ones(1,N),AreaY.*ones(1,N)];
dim = 2*N;%维度为2N,N个坐标点
5.算法结果


从结果来看,覆盖率在优化过程中不断上升,表明蜻蜓算法对覆盖优化起到了优化的作用。
6.参考文献
[1] 史朝亚. 基于PSO算法无线传感器网络覆盖优化的研究[D]. 南京理工大学.
7.MATLAB代码
相关文章:

智能优化算法应用:基于蜻蜓算法无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于蜻蜓算法无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于蜻蜓算法无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.蜻蜓算法4.实验参数设定5.算法结果6.参考文献7.MATLAB…...

【古诗生成AI实战】之二——项目架构设计
[1] 项目架构 在我们深入古诗生成AI项目的具体实践之前,让我们首先理解整个项目的架构。本项目的代码流程主要分为三个关键阶段: 1、数据处理阶段; 2、模型训练阶段; 3、文本生成阶段。 第一步:在数据处理阶段…...
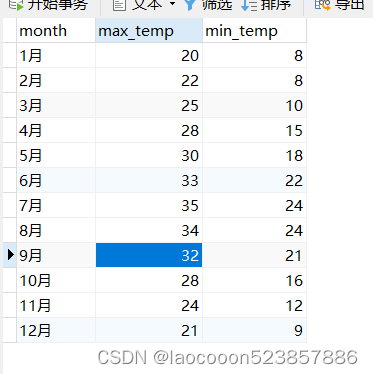
动态网页从数据库取信息,然后展示。
把数据库的驱动放在bin目录下。 通过servlet 读取数据库的内容,生成session,然后跨页面传给展示页。 package src;import java.io.IOException; import java.io.PrintWriter; import java.sql.Connection; import java.sql.DriverManager; import java.sql.ResultSe…...

单片机学习3——数码管
数码管,根据内部结构,可分为共阴极数码管和共阳极数码管。七段发光管加上一个小数点,共计8段。因此,我们对它编程的时候,刚好是用一个字节。 数码管的显示方式: 1)静态显示; 2&…...
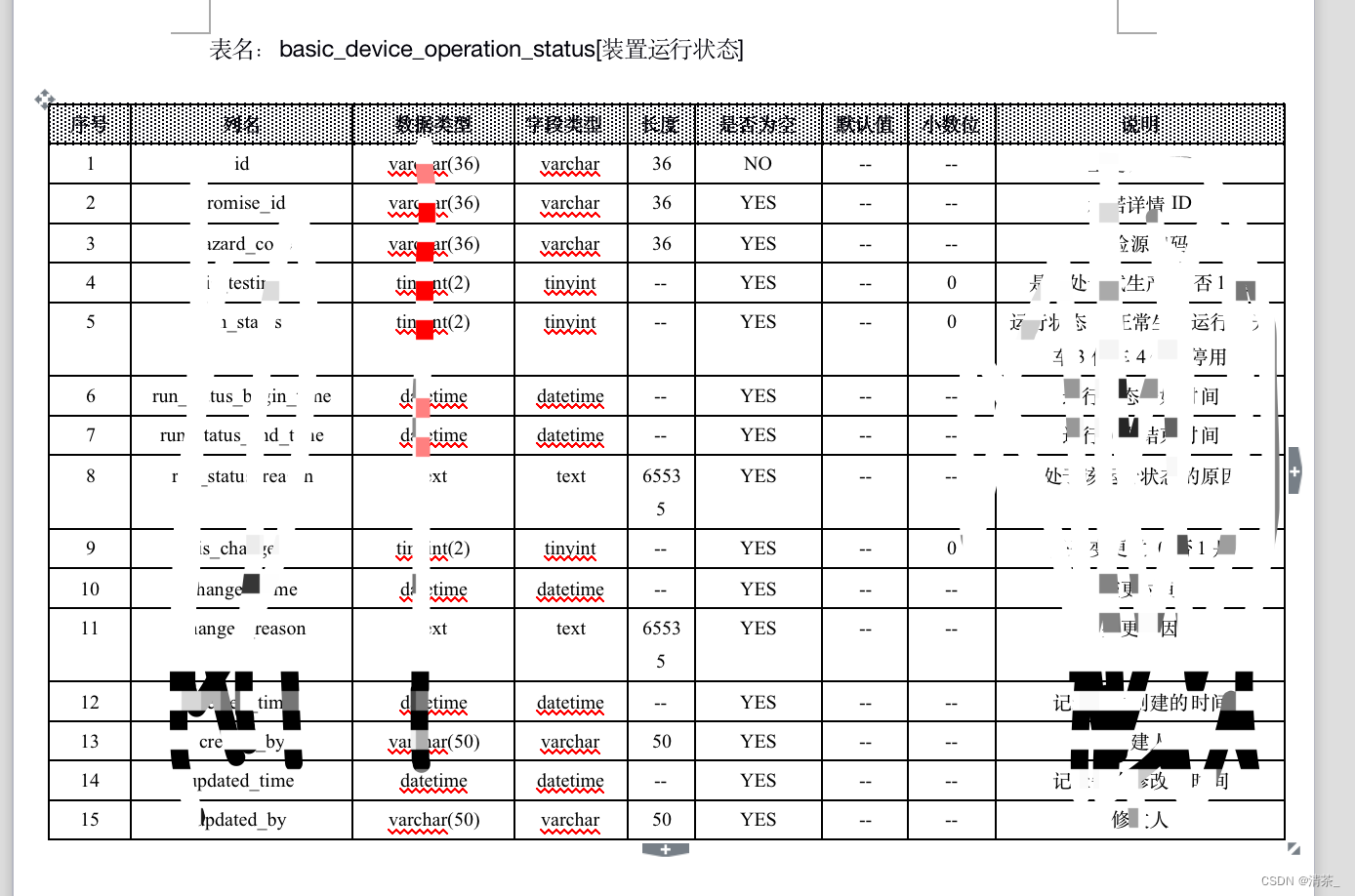
数据库表结构导出成Excel或Word格式
前言 该工具主要用于导出excel、word,方便快速编写《数据库设计文档》,同时可以快速查看表的结构和相关信息。 本博客仅作记录,最新源码已经支持多种数据库多种格式导出,有兴趣的可移步源码作者地址:https://gitee.co…...
School training competition ( Second )
A. Medium Number 链接 : Problem - 1760A - Codeforces 就是求三个数的中位数 : #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0); #define endl \nusing namespace std; typedef long long LL; const int N 2e510;inline void …...
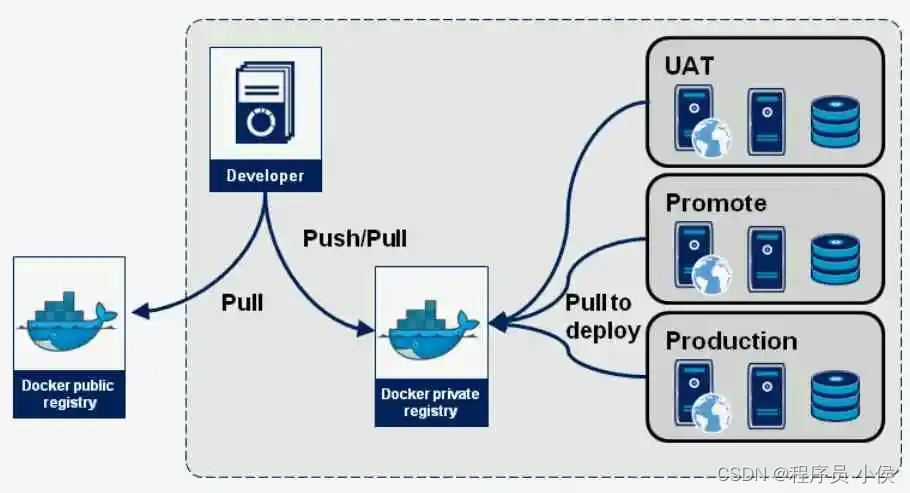
深度解析 Docker Registry:构建安全高效的私有镜像仓库
文章目录 什么是Docker Registry?Docker Hub vs. 私有RegistryDocker Hub:私有Registry: 如何构建私有Docker Registry?步骤一:安装Docker Registry步骤二:配置TLS(可选)步骤三&…...

leetcode 不同的二叉搜索树
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。 示例 1: 输入:n 3 输出:5 示例 2: 输入:n 1 输出:…...
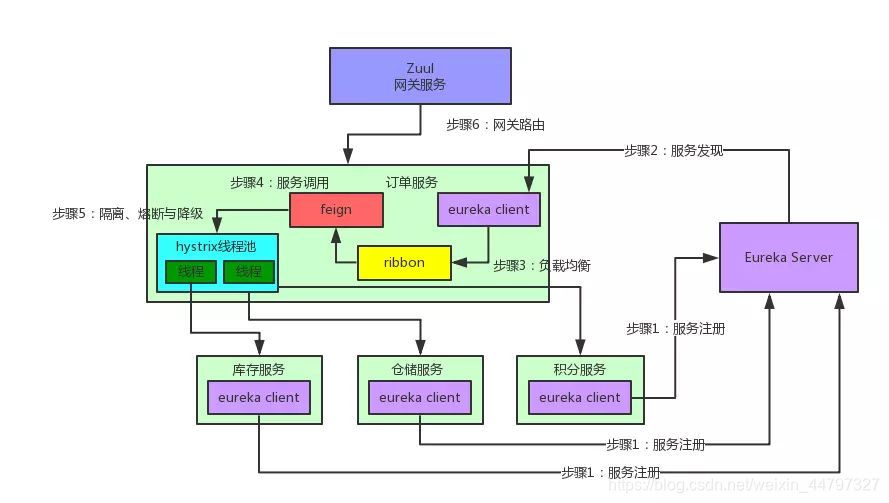
通俗易懂的spring Cloud;业务场景介绍 二、Spring Cloud核心组件:Eureka 、Feign、Ribbon、Hystrix、zuul
文章目录 通俗易懂的spring Cloud一、业务场景介绍二、Spring Cloud核心组件:Eureka三、Spring Cloud核心组件:Feign四、Spring Cloud核心组件:Ribbon五、Spring Cloud核心组件:Hystrix六、Spring Cloud核心组件:Zuul七…...

大数据预处理技术
文章目录 前言 大数据技术成为前沿专业 也是现在甚至未来的朝阳产业,大数据有分别是 数据预处理 数据存储 大数据处理和分析 数据可视化 部分组成 ,大数据行业有数据则称王,大数据的核心是数据本身 怎么获取有价值的数据呢?本章讲…...

跳表的学习记录
跳表(Skip List)是一种数据结构,它通过在多个层次上添加额外的前向指针来提高有序数据的搜索效率。跳表与其他常见的有序数据结构(如二叉搜索树、平衡树如AVL树和红黑树、B树等)相比,具有其独特的优缺点&am…...

电子学会C/C++编程等级考试2022年09月(二级)真题解析
C/C++等级考试(1~8级)全部真题・点这里 第1题:统计误差范围内的数 统计一个整数序列中与指定数字m误差范围小于等于X的数的个数。 时间限制:5000 内存限制:65536输入 输入包含三行: 第一行为N,表示整数序列的长度(N <= 100); 第二行为N个整数,整数之间以一个空格分…...
如何使用nginx部署静态资源
Nginx可以作为静态web服务器来部署静态资源,这个静态资源是指在服务端真实存在,并且能够直接展示的一些文件数据,比如常见的静态资源有html页面、css文件、js文件、图片、视频、音频等资源相对于Tomcat服务器来说,Nginx处理静态资…...
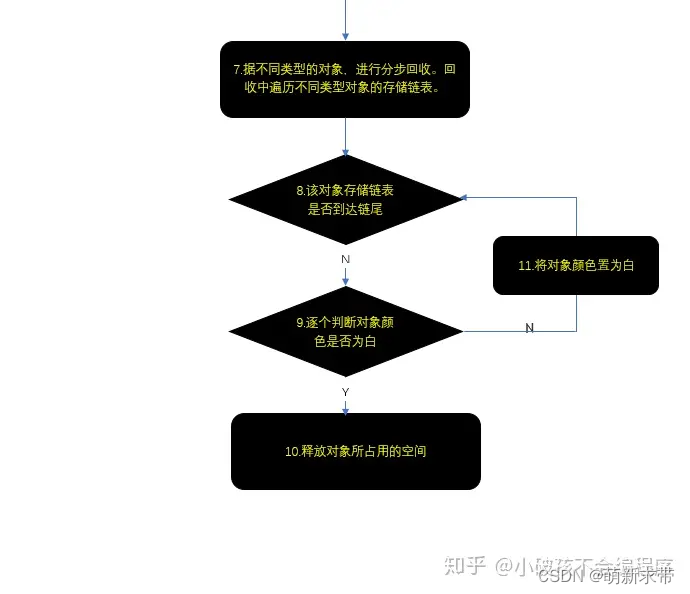
lua的gc原理
lua垃圾回收(Garbage Collect)是lua中一个比较重要的部分。由于lua源码版本变迁,目前大多数有关这个方面的文章都还是基于lua5.1版本,有一定的滞后性。因此本文通过参考当前的5.3.4版本的Lua源码,希望对Lua的GC算法有一个较为详尽的探讨。 L…...

redis作为缓存详解
目录 前言: 为什么说关系型数据库性能不高 如何提高MySQL并发量 缓存更新策略 定期更新 实时更新 内存淘汰策略 Redis内置的淘汰策略 缓存常见问题 缓存预热 缓存穿透 缓存雪崩 缓存击穿 前言: 对于缓存的理解,缓存目的就是为了…...
231127 刷题日报
这周值班。。多少写道题吧,保持每天的手感。老婆给买了lubuladong纸质书,加油卷。 1. 131. 分割回文串 写个这个吧,钉在耻辱柱上的题。 为啥没写出来: 1. 递归树没画对 把树枝只看做是1个字母,而且不清楚树枝和节点…...
【Linux】vim-多模式的文本编辑器
本篇文章内容和干货较多,希望对大家有所帮助👍 目录 一、vim的介绍 1.1 vi 与 vim的概念1.2 Vim 和 Vi 的一些对比 二、vim 模式之间的切换 2.1 进入vim2.2 [正常模式]切换到[插入模式]2.3 [插入模式]切换至[正常模式]2.4 [正常模式]切换至[底行模式…...

Ubuntu 启用 root 用户
在启用 root 用户之前,我们先来了解一下, ubuntu 命令的组成。 打开 ubuntu 的终端,现在的命令行是由 topeetubuntu:~$ 这几个字母组成,那么这几个字母都代表 什么意思呢? topeet …...
手摸手Element-ui路由VueRoute
后端WebAPI准备 https://router.vuejs.org/zh/guide/ https://v3.router.vuejs.org/zh/installation.html <template><el-table:data"tableData"style"width: 100%":row-class-name"tableRowClassName"><!-- <el-table-colum…...

探究Kafka原理-5.Kafka设计原理和生产者原理解析
👏作者简介:大家好,我是爱吃芝士的土豆倪,24届校招生Java选手,很高兴认识大家📕系列专栏:Spring源码、JUC源码、Kafka原理🔥如果感觉博主的文章还不错的话,请ὄ…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以?
Golang 面试经典题:map 的 key 可以是什么类型?哪些不可以? 在 Golang 的面试中,map 类型的使用是一个常见的考点,其中对 key 类型的合法性 是一道常被提及的基础却很容易被忽视的问题。本文将带你深入理解 Golang 中…...

MFC内存泄露
1、泄露代码示例 void X::SetApplicationBtn() {CMFCRibbonApplicationButton* pBtn GetApplicationButton();// 获取 Ribbon Bar 指针// 创建自定义按钮CCustomRibbonAppButton* pCustomButton new CCustomRibbonAppButton();pCustomButton->SetImage(IDB_BITMAP_Jdp26)…...

Cesium1.95中高性能加载1500个点
一、基本方式: 图标使用.png比.svg性能要好 <template><div id"cesiumContainer"></div><div class"toolbar"><button id"resetButton">重新生成点</button><span id"countDisplay&qu…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

CentOS下的分布式内存计算Spark环境部署
一、Spark 核心架构与应用场景 1.1 分布式计算引擎的核心优势 Spark 是基于内存的分布式计算框架,相比 MapReduce 具有以下核心优势: 内存计算:数据可常驻内存,迭代计算性能提升 10-100 倍(文档段落:3-79…...

高等数学(下)题型笔记(八)空间解析几何与向量代数
目录 0 前言 1 向量的点乘 1.1 基本公式 1.2 例题 2 向量的叉乘 2.1 基础知识 2.2 例题 3 空间平面方程 3.1 基础知识 3.2 例题 4 空间直线方程 4.1 基础知识 4.2 例题 5 旋转曲面及其方程 5.1 基础知识 5.2 例题 6 空间曲面的法线与切平面 6.1 基础知识 6.2…...

【Go】3、Go语言进阶与依赖管理
前言 本系列文章参考自稀土掘金上的 【字节内部课】公开课,做自我学习总结整理。 Go语言并发编程 Go语言原生支持并发编程,它的核心机制是 Goroutine 协程、Channel 通道,并基于CSP(Communicating Sequential Processes࿰…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

c#开发AI模型对话
AI模型 前面已经介绍了一般AI模型本地部署,直接调用现成的模型数据。这里主要讲述讲接口集成到我们自己的程序中使用方式。 微软提供了ML.NET来开发和使用AI模型,但是目前国内可能使用不多,至少实践例子很少看见。开发训练模型就不介绍了&am…...
