【案例教程】拉格朗日粒子扩散模式FLEXPART
拉格朗日粒子扩散模式FLEXPART通过计算点、线、面或体积源释放的大量粒子的轨迹，来描述示踪物在大气中长距离、中尺度的传输、扩散、干湿沉降和辐射衰减等过程。该模式既可以通过时间的前向运算来模拟示踪物由源区向周围的扩散，也可以通过后向运算来确定对于固定站点有影响的潜在源区分布。
本次内容采用“理论讲解+案例实战+动手实操+讨论互动”相结合的方式，抽丝剥茧、深入浅出地讲解FLEXPART扩散模式在研究大气污染物源-汇关系中需要掌握的经验和技巧。
【原文链接】： 【案例教程】拉格朗日粒子扩散模式FLEXPART实践技术应用
【方式】： 全套视频+永久回放+长期答疑群辅助+课件资料
【特色】：
原理深入浅出的讲解；
技巧方法讲解，提供所有案例数据及代码；
与项目案例相结合讲解实现方法，对接实际工作应用 ；
跟学上机操作、独立完成案例操作练习、全程问题跟踪解析；
专属助学群辅助巩固学习及实际工作应用交流，不定期召开线上答疑；
【证书及学时】：
学习本次内容可以获得《FLEXPART模式技术应用》专业技能培训证书及学时证明，网上可查。此证书可作为个人学习和知识更新、单位在职人员专业技能素质培养及单位人才聘用重要参考依据。
【内容介绍】：
《专题一、FLEXPART模式简介及Linux系统安装 》：
拉格朗日粒子扩散模式简介
FLEXPART模式简介及下载安装
Linux系统安装
FLEXPART 模式运行需要的其他工具
《专题二、FLEXPART模式数据输入、模式运行及结果输出 》：
气象场数据的获取
模式参数的设定
Pathnames内容设置
Command 参数设置
Release 参数设置
Outgrid 参数设置
FLEXPART模式运行
FLEXPART模式运行结果分析
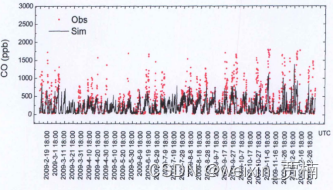
案例：对FLEXPART模式运行结果进行分析
《专题三、FLEXPART模式大气污染研究中的应用 》：
区域对受体点的源贡献
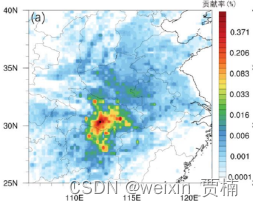
案例：不同区域对某一站点的贡献
其他应用
相关文章：
【案例教程】拉格朗日粒子扩散模式FLEXPART
拉格朗日粒子扩散模式FLEXPART通过计算点、线、面或体积源释放的大量粒子的轨迹，来描述示踪物在大气中长距离、中尺度的传输、扩散、干湿沉降和辐射衰减等过程。该模式既可以通过时间的前向运算来模拟示踪物由源区向周围的扩散，也可以通过后向运算来确定…...
试题 算法训练 自行车停放
问题描述 有n辆自行车依次来到停车棚，除了第一辆自行车外，每辆自行车都会恰好停放在已经在停车棚里的某辆自行车的左边或右边。(e.g.停车棚里已经有3辆自行车，从左到右编号为：3,5,1。现在编号为2的第4辆自行车要停在5号自行车的左…...
泛型与Map接口
Java学习之道 泛型 泛型这种参数类型可以用在类、方法和接口中，分别被称为泛型类，泛型方法，泛型接口 参数化类型：将类型由原来的具体的类型参数化，在使用/调用时传入具体的类型JDK5引入特性提供了安全检测机制…...
Unity Bug记录本
//个人记录，持续更新 1、将此代码挂载到空脚本上： bool flag (object)GetComponent<Camera>() null; bool flag1 (object)GetComponent<Text>() null; Debug.Log(flag"::"flag1); //输出结果：False::True bool…...
厉害)
B. The Number of Products)厉害
You are given a sequence a1,a2,…,ana1,a2,…,an consisting of nn non-zero integers (i.e. ai≠0ai≠0). You have to calculate two following values: the number of pairs of indices (l,r)(l,r) (l≤r)(l≤r) such that al⋅al1…ar−1⋅aral⋅al1…ar−1⋅ar is neg…...
)
一起Talk Android吧（第五百一十二回：自定义Dialog)
文章目录整体思路实现方法第一步第二步第三步第四步各位看官们大家好，上一回中咱们说的例子是"自定义Dialog主题",这一回中咱们说的例子是" 自定义Dialog"。闲话休提，言归正转， 让我们一起Talk Android吧！整体…...
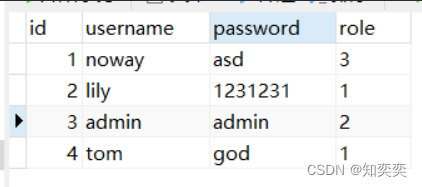
GinVueAdmin源码分析3-整合MySQL
目录文件结构数据库准备配置文件处理config.godb_list.gogorm_mysql.gosystem.go初始化数据库gorm.gogorm_mysql.go开始初始化测试数据库定义实体类 Userserviceapi开始测试！文件结构 本文章将使用到上一节创建的 CommonService 接口，用于测试连接数据库…...
大数据框架之Hadoop：MapReduce（三）MapReduce框架原理——MapReduce开发总结
在编写MapReduce程序时，需要考虑如下几个方面： 1、输入数据接口：InputFormat 默认使用的实现类是：TextInputFormatTextInputFormat的功能逻辑是：一次读一行文本，然后将该行的起始偏移量作为key࿰…...
requests---（4）发送post请求完成登录
前段时间写过一个通过cookies完成登录，今天我们写一篇通过post发送请求完成登录豆瓣网 模拟登录 1、首先找到豆瓣网的登录接口 打开豆瓣网站的登录接口，请求错误的账号密码，通过F12或者抓包工具找到登录接口 通过F12抓包获取到请求登录接口…...
Python抓取数据具体流程
之前看了一段有关爬虫的网课深有启发，于是自己也尝试着如如何过去爬虫百科“python”词条等相关页面的整个过程记录下来，方便后期其他人一起来学习。 抓取策略 确定目标：重要的是先确定需要抓取的网站具体的那些部分，下面实例是…...
【Python学习笔记】第二十四节 Python 正则表达式
一、正则表达式简介正则表达式（regular expression）是一个特殊的字符序列，它能帮助你方便的检查一个字符串是否与某种模式匹配。正则表达式是对字符串（包括普通字符（例如，a 到 z 之间的字母）和特…...
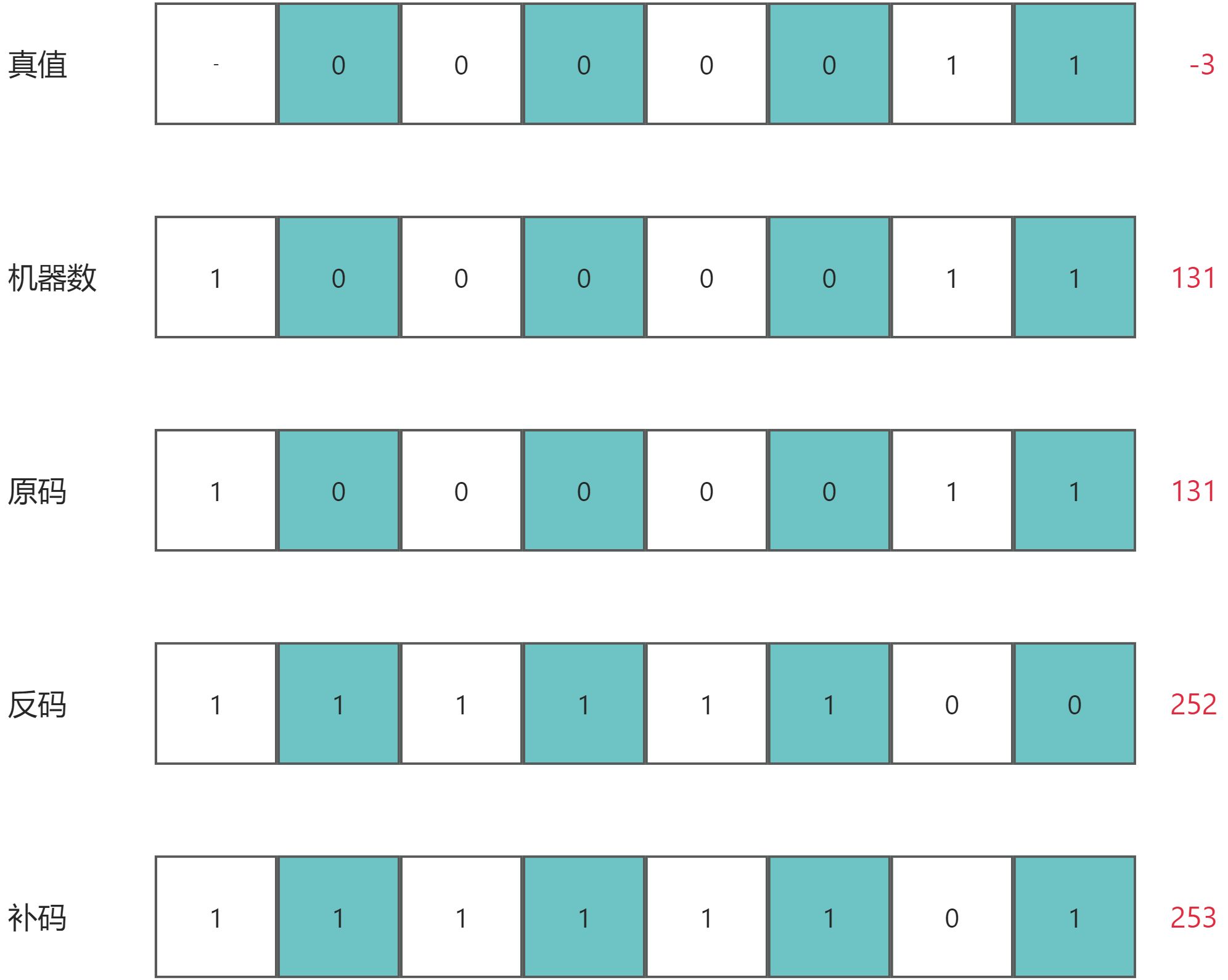
数字逻辑基础：原码、反码、补码
时间紧、不理解可以只看这里的结论 正数的原码、反码、补码相同。等于真值对应的机器码。 负数的原码等于机器码，反码为原码的符号位不变，其余各位按位取反。补码为反码1。 三种码的出现是为了解决计算问题并简化电路结构。 在原码和反码中，存…...
有限差分法-差商公式及其Matlab实现
2.1 有限差分法 有限差分法 (finite difference method)是一种数值求解偏微分方程的方法，它将偏微分方程中的连续变量离散化为有限个点上的函数值，然后利用差分逼近导数，从而得到一个差分方程组。通过求解差分方程组，可以得到原偏微分方程的数值解。 有限差分法是一种历史…...
高校就业信息管理系统
1引言 1.1编写目的 1.2背景 1.3定义 1.4参考资料 2程序系统的结构 3登录模块设计说明一 3.1程序描述 3.2功能 3.3性能 3.4输人项 3.5输出项 3.6算法 3.7流程逻辑 3.8接口 3.10注释设计 3.11限制条件 3.12测试计划 3.13尚未解决的问题 4注册模块设计说明 4.…...
【Java|golang】2373. 矩阵中的局部最大值
给你一个大小为 n x n 的整数矩阵 grid 。 生成一个大小为 (n - 2) x (n - 2) 的整数矩阵 maxLocal ，并满足： maxLocal[i][j] 等于 grid 中以 i 1 行和 j 1 列为中心的 3 x 3 矩阵中的 最大值 。 换句话说，我们希望找出 grid 中每个 3 x …...
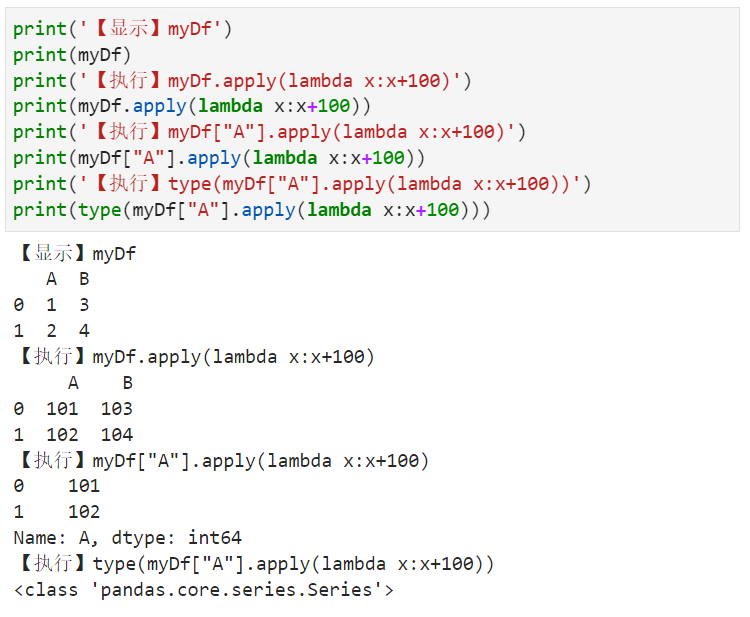
根据指定函数对DataFrame中各元素进行计算
【小白从小学Python、C、Java】【计算机等级考试500强双证书】【Python-数据分析】根据指定函数对DataFrame中各元素进行计算以下错误的一项是?import numpy as npimport pandas as pdmyDict{A:[1,2],B:[3,4]}myDfpd.DataFrame(myDict)print(【显示】myDf)print(myDf)print(【…...
【蓝桥杯集训·每日一题】AcWing 3502. 不同路径数
文章目录一、题目1、原题链接2、题目描述二、解题报告1、思路分析2、时间复杂度3、代码详解三、知识风暴一、题目 1、原题链接 3502. 不同路径数 2、题目描述 给定一个 nm 的二维矩阵，其中的每个元素都是一个 [1,9] 之间的正整数。 从矩阵中的任意位置出发…...
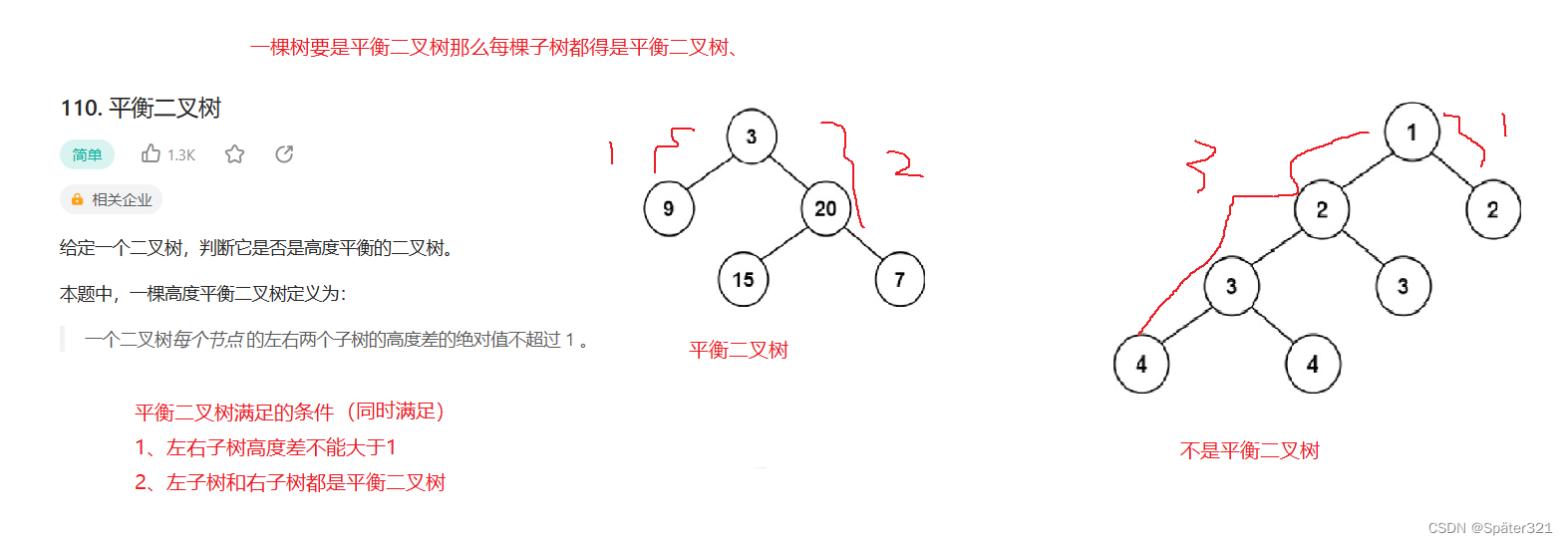
Java - 数据结构，二叉树
一、什么是树 概念 树是一种非线性的数据结构，它是由n（n>0）个有限结点组成一个具有层次关系的集合。把它叫做树是因为它看起来像一棵倒挂的树，也就是说它是根朝上，而叶朝下的。它具有以下的特点： 1、有…...
模拟QQ登录-课后程序(JAVA基础案例教程-黑马程序员编著-第十一章-课后作业)
【案例11-3】 模拟QQ登录 【案例介绍】 1.案例描述 QQ是现实生活中常用的聊天工具，QQ登录界面看似小巧、简单，但其中涉及的内容却很多，对于初学者练习Java Swing工具的使用非常合适。本案例要求使用所学的Java Swing知识，模拟实…...
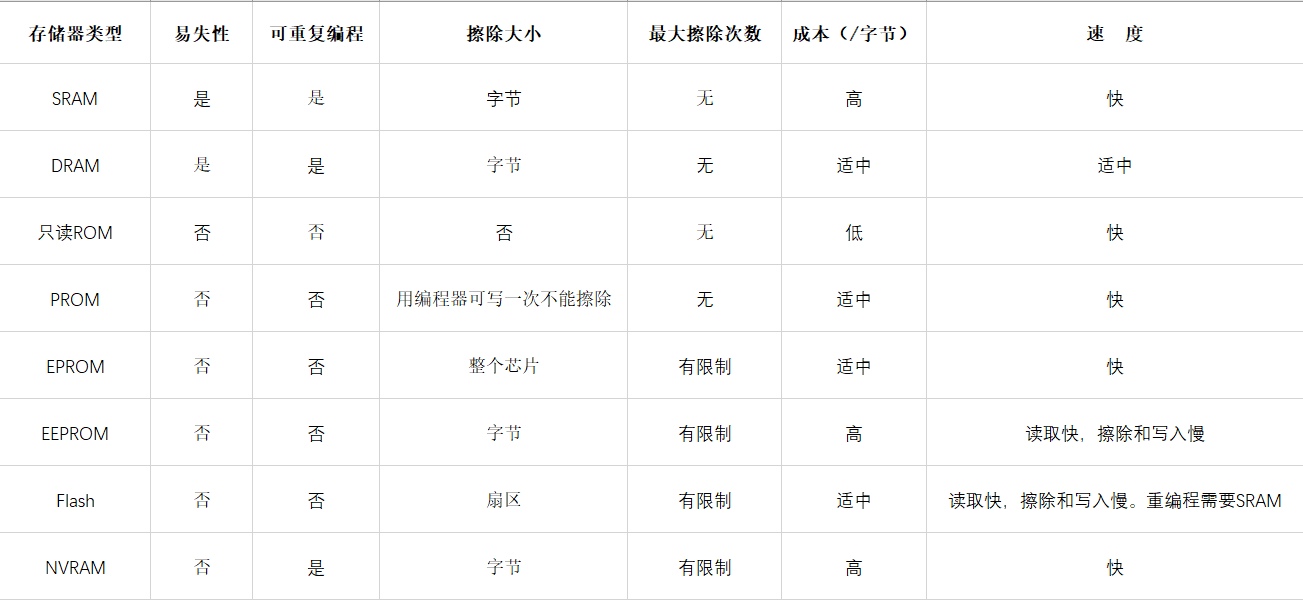
【壹】嵌入式系统硬件基础
随手拍拍💁♂️📷 日期: 2023.2.28 地点: 杭州 介绍: 日子像旋转毒马🐎，在脑海里转不停🤯 🌲🌲🌲🌲🌲 往期回顾 🌲🌲🌲…...
Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning（提示调优） 核心思想：固定预训练模型参数，仅学习额外的连续提示向量（通常是嵌入层的一部分）。实现方式：在输入文本前添加可训练的连续向量（软提示），模型只更新这些提示参数。优势：参数量少（仅提…...
前端倒计时误差!
提示：记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来？二、五大解决方案1. 动态校准法（基础版）2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...
线程同步：确保多线程程序的安全与高效！
全文目录： 开篇语前序前言第一部分：线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分：synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...
SCAU期末笔记 - 数据分析与数据挖掘题库解析
这门怎么题库答案不全啊日 来简单学一下子来 一、选择题（可多选） 将原始数据进行集成、变换、维度规约、数值规约是在以下哪个步骤的任务?(C) A. 频繁模式挖掘 B.分类和预测 C.数据预处理 D.数据流挖掘 A. 频繁模式挖掘：专注于发现数据中…...
【SQL学习笔记1】增删改查+多表连接全解析（内附SQL免费在线练习工具）
可以使用Sqliteviz这个网站免费编写sql语句，它能够让用户直接在浏览器内练习SQL的语法，不需要安装任何软件。 链接如下： sqliteviz 注意： 在转写SQL语法时，关键字之间有一个特定的顺序，这个顺序会影响到…...
SpringTask-03.入门案例
一.入门案例 启动类： package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...
什么？连接服务器也能可视化显示界面？：基于X11 Forwarding + CentOS + MobaXterm实战指南
文章目录 什么是X11？环境准备实战步骤1️⃣ 服务器端配置（CentOS）2️⃣ 客户端配置（MobaXterm）3️⃣ 验证X11 Forwarding4️⃣ 运行自定义GUI程序(Python示例)5️⃣ 成功效果
Netty从入门到进阶（二）
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架，用于…...
SQL慢可能是触发了ring buffer
简介 最近在进行 postgresql 性能排查的时候，发现 PG 在某一个时间并行执行的 SQL 变得特别慢。最后通过监控监观察到并行发起得时间 buffers_alloc 就急速上升，且低水位伴随在整个慢 SQL，一直是 buferIO 的等待事件，此时也没有其他会话的争抢。SQL 虽然不是高效 SQL ，但…...
C++课设：简易日历程序（支持传统节假日 + 二十四节气 + 个人纪念日管理）
名人说：路漫漫其修远兮，吾将上下而求索。—— 屈原《离骚》 创作者：Code_流苏(CSDN)（一个喜欢古诗词和编程的Coder😊） 专栏介绍：《编程项目实战》 目录 一、为什么要开发一个日历程序？1. 深入理解时间算法2. 练习面向对象设计3. 学习数据结构应用二、核心算法深度解析…...