智能优化算法应用:基于浣熊算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于浣熊算法3D无线传感器网络(WSN)覆盖优化 - 附代码
文章目录
- 智能优化算法应用:基于浣熊算法3D无线传感器网络(WSN)覆盖优化 - 附代码
- 1.无线传感网络节点模型
- 2.覆盖数学模型及分析
- 3.浣熊算法
- 4.实验参数设定
- 5.算法结果
- 6.参考文献
- 7.MATLAB代码
摘要:本文主要介绍如何用浣熊算法进行3D无线传感器网(WSN)覆盖优化。
1.无线传感网络节点模型
本文主要基于0/1模型,进行寻优。在二维平面上传感器节点的感知范围是一个以节点为圆心,半径为 R n R_n Rn的圆形区域,该圆形区域通常被称为该节点的“感知圆盘”, R n R_n Rn称为传感器节点的感知半径,感知半径与节点内置传感器件的物理特性有关,假设节点 n n n的位置坐标为 ( x n , y n , z n ) (x_n,y_n,z_n) (xn,yn,zn)在0-1感知模型中,对于平面上任意一点 p ( x p , y p , z p ) p(x_p,y_p,z_p) p(xp,yp,zp),则节点 n n n监测到区域内点 p p p的事件发生概率为:
P r ( n , p ) = { 1 , d ( n , p ) ≤ R n 0 , e s l e (1) P_r(n,p)=\begin{cases}1, \,d(n,p)\leq R_n\\ 0,\, esle \end{cases}\tag{1} Pr(n,p)={1,d(n,p)≤Rn0,esle(1)
其中 d ( n , p ) = ( x n − x p ) 2 + ( y n − y p ) 2 + ( z n − z p ) 2 d(n,p)=\sqrt{(x_n-x_p)^2+(y_n-y_p)^2 + (z_n-z_p)^2} d(n,p)=(xn−xp)2+(yn−yp)2+(zn−zp)2为点和之间的欧式距离。
2.覆盖数学模型及分析
现假定目标监测区域为二维平面,在区域 A r e a Area Area上投放同型结构传感器节点的数目为N,每个节点的位置坐标值假设已被初始化赋值,且节点的感知半径r。传感器节点集则表示为:
N o d e { x 1 , . . . , x N } (2) Node\{x_1,...,x_N\} \tag{2} Node{x1,...,xN}(2)
其中 n o d e i = { x i , y i , z i , r } node_i=\{x_i,y_i,z_i,r\} nodei={xi,yi,zi,r},表示以节点 ( x i , y i , z i ) (x_i,y_i,z_i) (xi,yi,zi)为圆心,r为监测半径的球,假定监测区域 A r e a Area Area被数字化离散为 m ∗ n ∗ l m*n*l m∗n∗l个空间点,空间点的坐标为 ( x , y , z ) (x,y,z) (x,y,z),目标点与传感器节点间的距离为:
d ( n o d e i , p ) = ( x i − x ) 2 + ( y i − y ) 2 + ( z i − z ) 2 (3) d(node_i,p)=\sqrt{(x_i-x)^2+(y_i-y)^2 + (z_i-z)^2}\tag{3} d(nodei,p)=(xi−x)2+(yi−y)2+(zi−z)2(3)
目标区域内点被传感器节点所覆盖的事件定义为 c i c_i ci。则该事件发生的概率 P c i P{c_i} Pci即为点 ( x , y , z ) (x,y,z) (x,y,z)被传感器节点 n o d e i node_i nodei所覆盖的概率:
P c o v ( x , y , z , n o d e i ) = { 1 , i f d ( n o d e i , p ) ≤ r 0 , e s l e (4) P_{cov}(x,y,z,node_i)=\begin{cases}1, if\,d(node_i,p)\leq r\\ 0,\, esle \end{cases}\tag{4} Pcov(x,y,z,nodei)={1,ifd(nodei,p)≤r0,esle(4)
我们将所有的传感器节点在目标监测环境中的区域覆盖率 C o v e r R a t i o CoverRatio CoverRatio定义为传感器节点集的覆盖面积与监测区域的面积之比,如公式所示:
C o v e r R a t i o = ∑ P c o v m ∗ n ∗ l (5) CoverRatio = \frac{\sum P_{cov}}{m*n*l}\tag{5} CoverRatio=m∗n∗l∑Pcov(5)
那我们的最终目标就是找到一组节点使得覆盖率最大。
3.浣熊算法
浣熊算法原理请参考:https://blog.csdn.net/u011835903/article/details/130538719
浣熊算法是寻找最小值。于是适应度函数定义为未覆盖率最小,即覆盖率最大。如下:
f u n = a r g m i n ( 1 − C o v e r R a t i o ) = a r g m i n ( 1 − ∑ P c o v m ∗ n ∗ l ) (6) fun = argmin(1 - CoverRatio) = argmin(1-\frac{\sum P_{cov}}{m*n*l}) \tag{6} fun=argmin(1−CoverRatio)=argmin(1−m∗n∗l∑Pcov)(6)
4.实验参数设定
无线传感器覆盖参数设定如下:
%% 设定WNS覆盖参数,
%% 默认输入参数都是整数,如果想定义小数,请自行乘以系数变为整数再做转换。
%% 比如范围1*1,R=0.03可以转换为100*100,R=3;
%区域范围为AreaX*AreaY*AreaZ
AreaX = 100;
AreaY = 100;
AreaZ = 100;
N = 20 ;%覆盖节点数
R = 15;%通信半径浣熊算法参数如下:
%% 设定浣熊优化参数
pop=30; % 种群数量
Max_iteration=30; %设定最大迭代次数
lb = ones(1,3*N);
ub = [AreaX.*ones(1,N),AreaY.*ones(1,N),AreaZ.*ones(1,N)];
dim = 3*N;%维度为3N,N个坐标点
5.算法结果

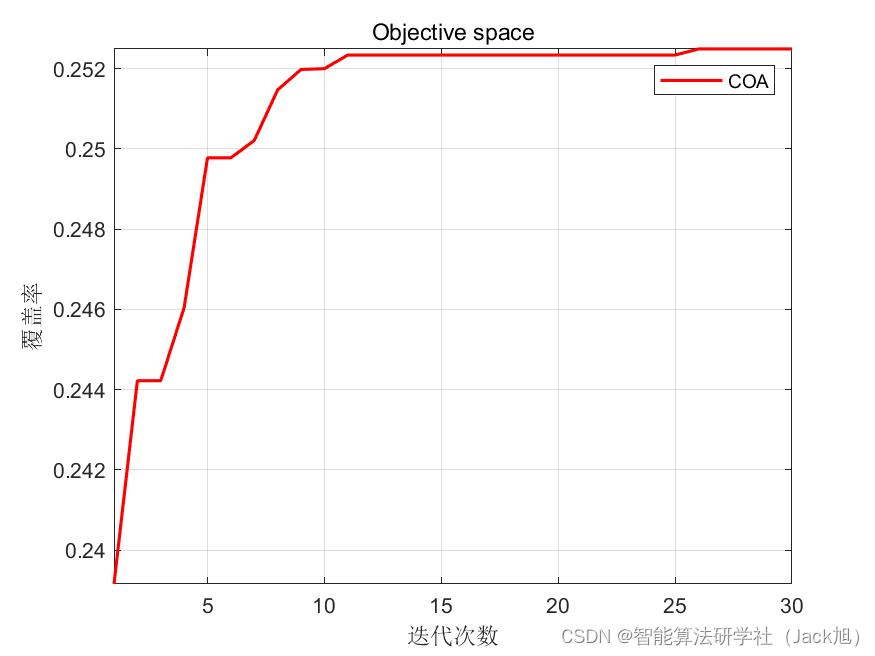
从结果来看,覆盖率在优化过程中不断上升。表明浣熊算法对覆盖优化起到了优化的作用。
6.参考文献
[1] 史朝亚. 基于PSO算法无线传感器网络覆盖优化的研究[D]. 南京理工大学.
7.MATLAB代码
相关文章:

智能优化算法应用:基于浣熊算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于浣熊算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于浣熊算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.浣熊算法4.实验参数设定5.算法结果6.参考文献7.MA…...

c++ qt QtWidgetsApplication 项目 使用外部ui
1 包含生成的UI头文件: 例如,如果你的Qt Designer的.ui文件名为test.ui,那么生成的头文件通常为ui_test.h。 #include "ui_test.h"2 实例化UI类:.h文件中实例化ui 在你的主要类的头文件中,你通常会声明一个U…...
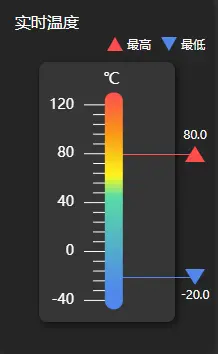
使用React 18、Echarts和MUI实现温度计
关键词 React 18 Echarts和MUI 前言 在本文中,我们将结合使用React 18、Echarts和MUI(Material-UI)库,展示如何实现一个交互性的温度计。我们将使用Echarts绘制温度计的外观,并使用MUI创建一个漂亮的用户界面。 本文…...
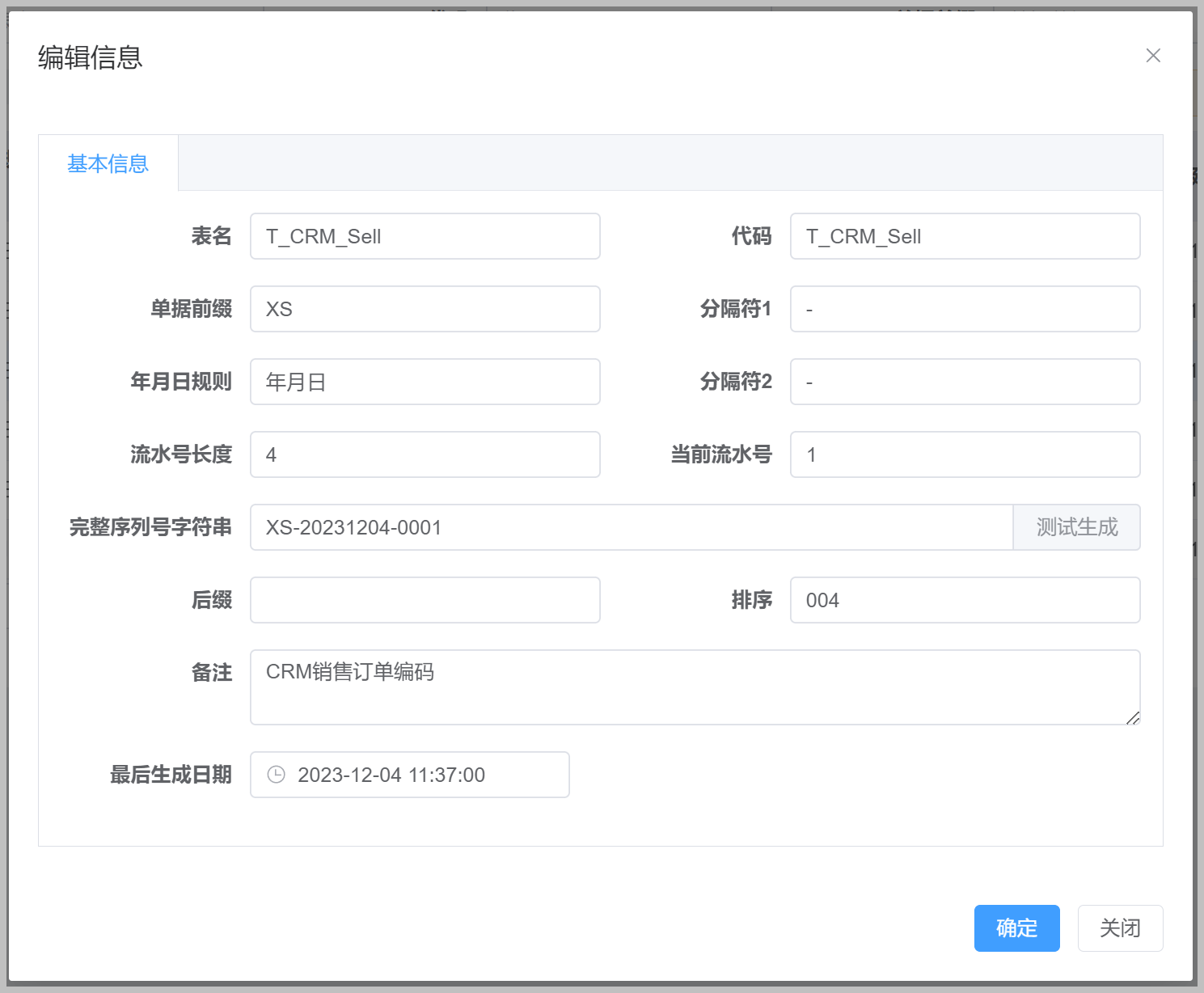
使用代码生成工具快速开发应用-结合后端Web API提供接口和前端页面快速生成,实现通用的业务编码规则管理
1、通用的业务编码规则的管理功能 在前面随笔我们介绍了一个通用的业务编码规则的管理功能,通过代码生成工具Database2Sharp一步步的生成相关的后端和Winform、WPF的界面,进行了整合,通过利用代码生成工具Database2sharp生成节省了常规功能的…...
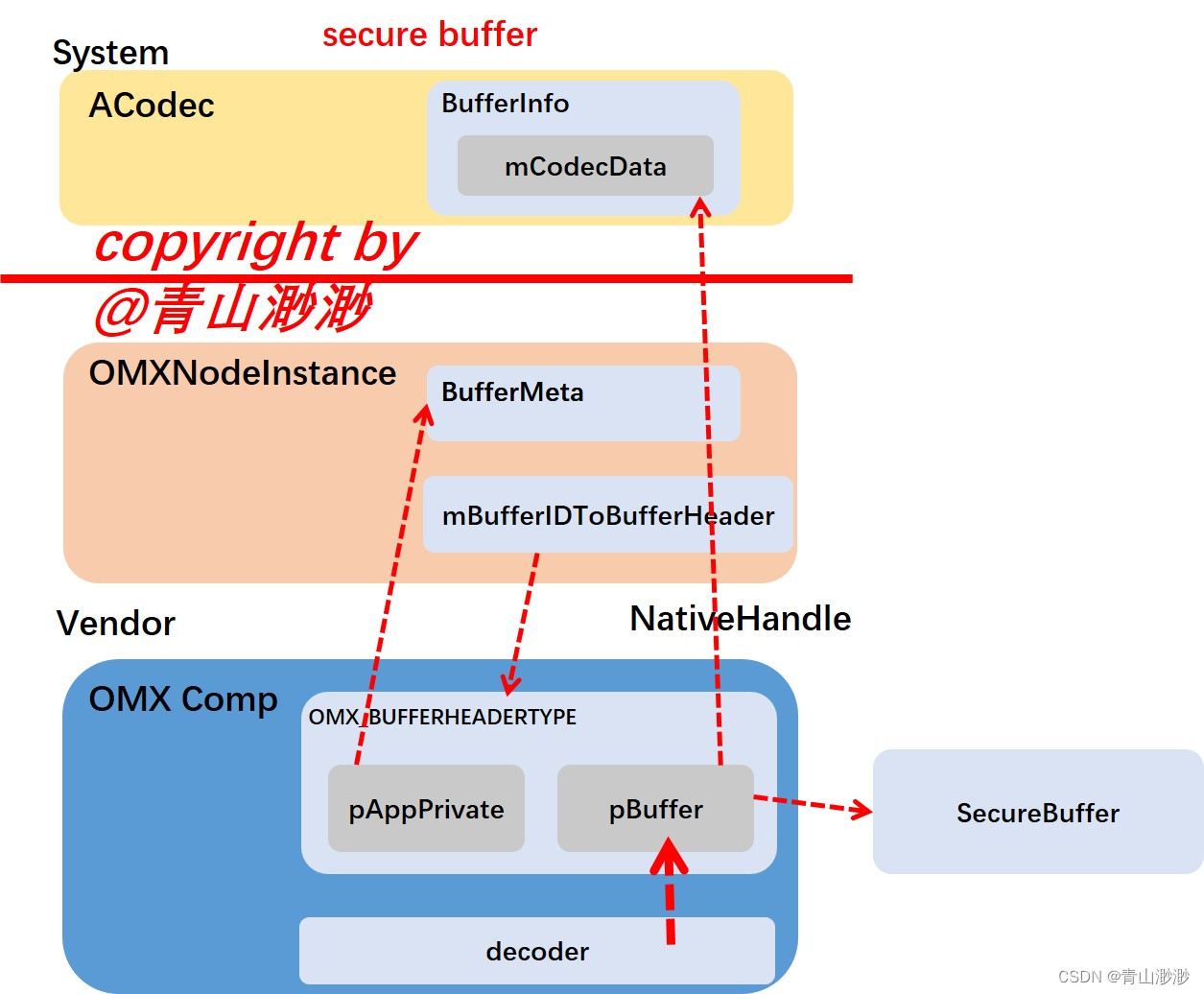
Android 13 - Media框架(26)- OMXNodeInstance(三)
上一节我们了解了OMXNodeInstance中的端口定义,这一节我们一起来学习ACodec、OMXNode、OMX 组件使用的 buffer 到底是怎么分配出来的,以及如何关联起来的。(我们只会去了解 graphic buffer的创建、input bytebuffer的创建、secure buffer的创…...
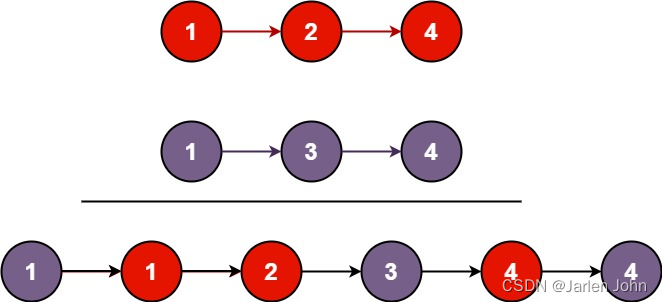
力扣题目学习笔记(OC + Swift)21. 合并两个有序链表
21. 合并两个有序链表 将两个升序链表合并为一个新的 升序 链表并返回。新链表是通过拼接给定的两个链表的所有节点组成的。 链表解题经典三把斧: 哑巴节点栈快慢指针 此题比较容易想到的解法是迭代法,生成哑巴节点,然后迭代生成后续节点。…...
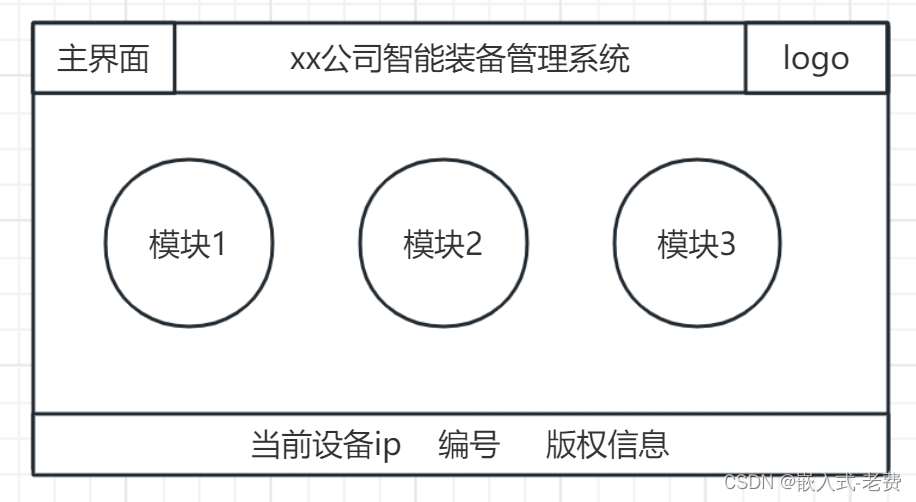
C# WPF上位机开发(windows pad上的应用)
【 声明:版权所有,欢迎转载,请勿用于商业用途。 联系信箱:feixiaoxing 163.com】 大部分同学可能都认为c# wpf只能用在pc端。其实这是一种误解。c# wpf固然暂时只能运行在windows平台上面,但是windows平台不仅仅是电脑…...

Word使用技巧【开题报告】
1、修改目录:选中目录,点击更新域。 2、更改或删除单个页面上的页眉或页脚 3、借助其他软件在Word导入参考文献 利用zetero导入文献:安装zetero 解决参考文献插入问题 在Word中插入文献操作步骤 英文文献出现“等”,如何解决 Zote…...

电子学会C/C++编程等级考试2022年06月(七级)真题解析
C/C++等级考试(1~8级)全部真题・点这里 第1题:有多少种二叉树 输入n(1<n<13),求n个结点的二叉树有多少种形态 时间限制:1000 内存限制:65536输入 整数n输出 答案 样例输入 3样例输出 5 答案: //参考答案 #include<bits/stdc++.h> using namespace std; …...
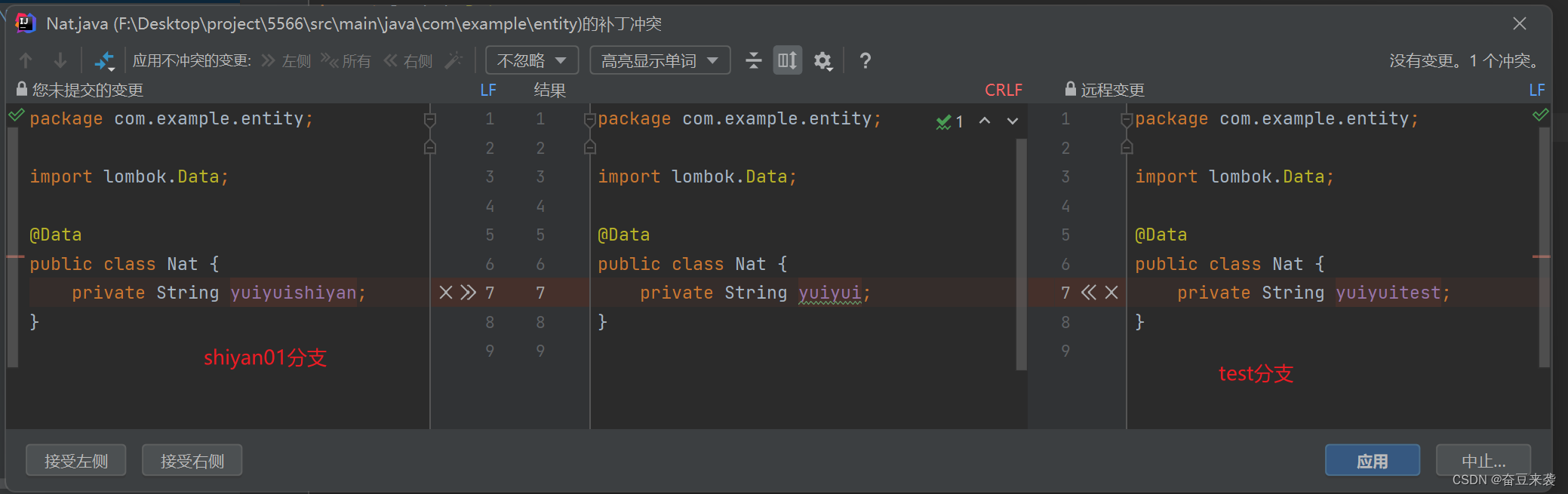
git中的smart checkout和force checkout
切换分支时出现了这个问题: 这是因为shiyan01分支修改了代码,但是没有commit, 所以在切换到test分支的时候弹出这个窗口 一、smart checkout(智能签出) 会把shiyan01分支的改动内容带到test分支。合并处理后的内容就变成了test分支的内容,而shiyan01分支的改动会被…...

vue3整合Element-Plus,极速上手。
条件分页查询: 需求分析: form表单 Button按钮 Table表格 Pagination分页 页面布局: 搜索表单: 如果表单封装的数据较多,建议绑定到一个对象中。 …...

学习Vue2.x
文章目录 一、使用Vue脚手架1.ref和props属性2.mixin混入3.组件化编码流程4.webStorage5.组件自定义事件6.全局事件总线7.消息订阅与发布 二、使用步骤1.引入库 一、使用Vue脚手架 1.ref和props属性 ref属性: (1)被用来给元素或子组件注册应…...
)
新手如何快速熟悉代码,写出东西(持续更新)
目录 第一章、最小编程任务的设想1.1)程序员入门会遇到的问题1.2)最小编程任务的设想1.3)编程逻辑1.4)具体需求 第二章、最小编程单元的练习2.1)代码/需求方面2.1.1)初级练习2.1.2)中级练习2.1.…...
)
11-网络安全框架及模型-软件安全能力成熟度模型(SSCMM)
目录 软件安全能力成熟度模型 1 背景概述 2 主要内容 3 成熟度等级定义 4 关键过程和实践 5 评估方法 6 改进建议 7 持续改进 8 主要价值 9 应用场景 10 优势和局限性 备注 软件安全能力成熟度模型 1 背景概述 SSCMM模型是软件安全能力成熟度模型,它描…...

Linux操作系统基础知识点
Linux是一种计算机操作系统,其内核由林纳斯本纳第克特托瓦兹(Linus Benedict Torvalds)于1991年首次发布。Linux操作系统通常与GNU套件一起使用,因此也被称为GNU/Linux。它是一种类UNIX的操作系统,设计为多用户、多任务…...
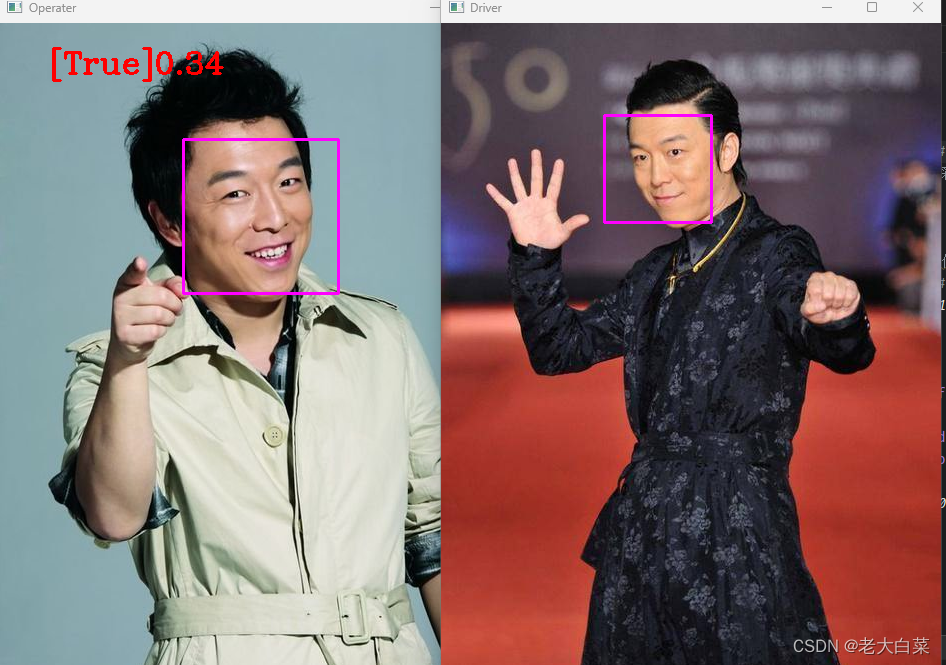
python 通过opencv及face_recognition识别人脸
效果: 使用Python的cv2库和face_recognition库来进行人脸检测和比对的 0是代表一样 认为是同一人。 代码: pip install opencv-python pip install face_recognition# 导入cv2库,用于图像处理 import cv2 # 导入face_recognition库&#…...

Android开发中常见的Hook技术有哪些?
Hook技术介绍 Hook技术是一种在软件开发中常见的技术,它允许开发者在特定的事件发生时插入自定义的代码逻辑。常见的应用场景包括在函数调用前后执行特定的操作,或者在特定的事件发生时触发自定义的处理逻辑。 在Android开发中,Hook通常是通…...

【linux c多线程】线程的创建,线程信息的获取,获取线程返回值
线程创建 专栏内容: 参天引擎内核架构 本专栏一起来聊聊参天引擎内核架构,以及如何实现多机的数据库节点的多读多写,与传统主备,MPP的区别,技术难点的分析,数据元数据同步,多主节点的情况下对…...

MFC或QT中,自绘控件的目的和实现步骤
MFC自绘控件的步骤 自绘控件的目的是为了能够自定义控件的外观、行为和交互方式,以满足特定的需求,同时增强应用程序的用户体验。 实现步骤如下: 1、创建一个继承自MFC控件基类(如CButton、CStatic等)的自定义控件类…...
)
ceph集群搭建详细教程(ceph-deploy)
ceph-deploy比较适合生产环境,不是用cephadm搭建。相对麻烦一些,但是并不难,细节把握好就行,只是命令多一些而已。 实验环境 服务器主机public网段IP(对外服务)cluster网段IP(集群通信&#x…...
:OpenBCI_GUI:从环境搭建到数据可视化(下))
脑机新手指南(八):OpenBCI_GUI:从环境搭建到数据可视化(下)
一、数据处理与分析实战 (一)实时滤波与参数调整 基础滤波操作 60Hz 工频滤波:勾选界面右侧 “60Hz” 复选框,可有效抑制电网干扰(适用于北美地区,欧洲用户可调整为 50Hz)。 平滑处理&…...

Day131 | 灵神 | 回溯算法 | 子集型 子集
Day131 | 灵神 | 回溯算法 | 子集型 子集 78.子集 78. 子集 - 力扣(LeetCode) 思路: 笔者写过很多次这道题了,不想写题解了,大家看灵神讲解吧 回溯算法套路①子集型回溯【基础算法精讲 14】_哔哩哔哩_bilibili 完…...

大语言模型如何处理长文本?常用文本分割技术详解
为什么需要文本分割? 引言:为什么需要文本分割?一、基础文本分割方法1. 按段落分割(Paragraph Splitting)2. 按句子分割(Sentence Splitting)二、高级文本分割策略3. 重叠分割(Sliding Window)4. 递归分割(Recursive Splitting)三、生产级工具推荐5. 使用LangChain的…...

MMaDA: Multimodal Large Diffusion Language Models
CODE : https://github.com/Gen-Verse/MMaDA Abstract 我们介绍了一种新型的多模态扩散基础模型MMaDA,它被设计用于在文本推理、多模态理解和文本到图像生成等不同领域实现卓越的性能。该方法的特点是三个关键创新:(i) MMaDA采用统一的扩散架构…...

C++ Visual Studio 2017厂商给的源码没有.sln文件 易兆微芯片下载工具加开机动画下载。
1.先用Visual Studio 2017打开Yichip YC31xx loader.vcxproj,再用Visual Studio 2022打开。再保侟就有.sln文件了。 易兆微芯片下载工具加开机动画下载 ExtraDownloadFile1Info.\logo.bin|0|0|10D2000|0 MFC应用兼容CMD 在BOOL CYichipYC31xxloaderDlg::OnIni…...

AspectJ 在 Android 中的完整使用指南
一、环境配置(Gradle 7.0 适配) 1. 项目级 build.gradle // 注意:沪江插件已停更,推荐官方兼容方案 buildscript {dependencies {classpath org.aspectj:aspectjtools:1.9.9.1 // AspectJ 工具} } 2. 模块级 build.gradle plu…...

#Uniapp篇:chrome调试unapp适配
chrome调试设备----使用Android模拟机开发调试移动端页面 Chrome://inspect/#devices MuMu模拟器Edge浏览器:Android原生APP嵌入的H5页面元素定位 chrome://inspect/#devices uniapp单位适配 根路径下 postcss.config.js 需要装这些插件 “postcss”: “^8.5.…...

水泥厂自动化升级利器:Devicenet转Modbus rtu协议转换网关
在水泥厂的生产流程中,工业自动化网关起着至关重要的作用,尤其是JH-DVN-RTU疆鸿智能Devicenet转Modbus rtu协议转换网关,为水泥厂实现高效生产与精准控制提供了有力支持。 水泥厂设备众多,其中不少设备采用Devicenet协议。Devicen…...

comfyui 工作流中 图生视频 如何增加视频的长度到5秒
comfyUI 工作流怎么可以生成更长的视频。除了硬件显存要求之外还有别的方法吗? 在ComfyUI中实现图生视频并延长到5秒,需要结合多个扩展和技巧。以下是完整解决方案: 核心工作流配置(24fps下5秒120帧) #mermaid-svg-yP…...

AD学习(3)
1 PCB封装元素组成及简单的PCB封装创建 封装的组成部分: (1)PCB焊盘:表层的铜 ,top层的铜 (2)管脚序号:用来关联原理图中的管脚的序号,原理图的序号需要和PCB封装一一…...
