MySQL定时备份实现
一、备份数据库
–all-databases 备份所有数据库
/opt/mysqlcopy/all_$(date “+%Y-%m-%d %H:%M:%S”).sql 备份地址
docker exec -it 容器名称 sh -c "mysqldump -u root -p'password' --all-databases > '/opt/mysqlcopy/all_$(date "+%Y-%m-%d %H:%M:%S").sql'"
使用方式
直接使用

可能会提示 mysqldump: [Warning] Using a password on the command line interface can be insecure.
意思是密码直接明文显示会不安全,emm~,可以不管
查看备份的文件
进入容器使用 ls -lk 查看
二、定时备份使用 crontab
安装 crontab
apt update
apt install crontab
检验安装
crontab -V

新建任务文件
文件内容如下
#!/bin/bash
docker exec mysql sh -c "mysqldump -u root -p'123456' --all-databases > '/opt/mysqlcopy/all_$(date "+%Y-%m-%d %H:%M:%S").sql'"新建定时任务
输入命令
crontab -e
# 表示每2分钟备份一次
*/2 * * * *
# 表示每天凌晨3点备份一次
0 3 * * *
# 表示输出日志
> /opt/cron_output.log 2>&1
编辑完保存退出
三、解决报错
如果没效果,那么就打开/opt/cron_output.log文件看日志
1、/opt/crontab/copyMysql.sh: line 2: $‘\r’: command not found
这是说脚本文件中包含了 Windows 格式的换行符 (\r\n,Carriage Return + Line Feed)。在 Linux 系统中,通常使用 Unix 格式的换行符 (\n,Line Feed)。
解决办法,不要在windows系统里编辑,直接使用vim编辑就行
2、the input device is not a TTY
通常表示脚本试图在一个非交互式(non-interactive)的环境中执行需要交互的命令
解决办法,在你的脚本中,这可能与 docker exec -it 命令有关,该命令通常用于交互式地在容器中执行命令。
去掉 -it 参数,因为在非交互式环境中执行命令时,一般不需要 -it。
相关文章:

MySQL定时备份实现
一、备份数据库 –all-databases 备份所有数据库 /opt/mysqlcopy/all_$(date “%Y-%m-%d %H:%M:%S”).sql 备份地址 docker exec -it 容器名称 sh -c "mysqldump -u root -ppassword --all-databases > /opt/mysqlcopy/all_$(date "%Y-%m-%d %H:%M:%S").sq…...
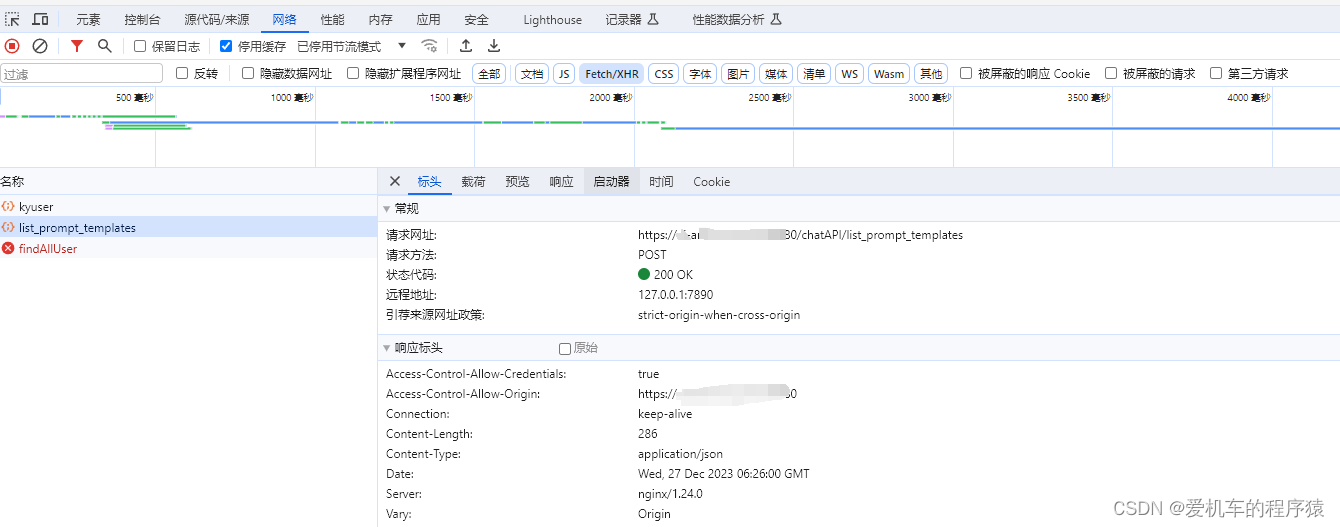
Nginx 不同源Https请求Http 报strict-origin-when-cross-origin
原因: nginx代理配置url指向只开放了/* 而我/*/*多了一层路径 成功:...

openGauss学习笔记-175 openGauss 数据库运维-备份与恢复-导入数据-管理并发写入操作示例
文章目录 openGauss学习笔记-175 openGauss 数据库运维-备份与恢复-导入数据-管理并发写入操作示例175.1 相同表的INSERT和DELETE并发175.2 相同表的并发INSERT175.3 相同表的并发UPDATE175.4 数据导入和查询的并发 openGauss学习笔记-175 openGauss 数据库运维-备份与恢复-导入…...

pnpm、npm、yarn是什么?怎么选择?
pnpm、npm、yarn三者是前端常用的包管理器,那么他们有什么区别呢? 1. npm (Node Package Manager) npm是Node.js的默认包管理器。自Node.js发布以来,npm就一直作为它的一个组成部分存在,因此,安装Node.js时也会自动安…...

MySQL8 一键部署
#!/bin/bash ### 定义变量 mysql_download_urlhttps://cdn.mysql.com//Downloads/MySQL-8.0/mysql-8.0.33-linux-glibc2.12-x86_64.tar.xz mysql_package_namemysql-8.0.33-linux-glibc2.12-x86_64.tar.xz mysql_dec_namemysql-8.0.33-linux-glibc2.12-x86_64 mysql_download_…...

12 UVM Driver
目录 12.1 uvm_driver class hierarchy 12.2 How to write driver code? 12.3 UVM Driver example 12.4 How to get sequence items from the sequencer? 12.5 UVM driver methods 12.5.1 Using get_next_item/ try_next_item and item_done methods 12.5.2 Using get…...

“暂存”校验逻辑探讨
1、背景 在业务中可能会遇到这种场景,前端页面元素多且复杂,一次性填完提交耗时很长,中间中断面临着丢失数据的风险。针对这个问题,“暂存”应运而生。 那“暂存”的时候,是否需要对数据校验,如何进行校验…...
探究element-ui 2.15.8中<el-input>的keydown事件无效问题
一、问题描述 今天看到一个问题,在用Vue2element-ui 2.15.8开发时,使用input组件绑定keydown事件没有任何效果。 <template><div id"app"><el-input v-model"content" placeholder"请输入" keydown&quo…...

Unity 代码控制Text自适应文本高度
在使用代码给Text赋值时,且文本有多段,并需要根据实际文本高度适配Text组件的高度时,可以使用以下方法: //Text文本 public TextMeshProUGUI text;void Start() {//代码赋值文本text.text "好!\n很好!\n非常好!";//获…...

TiDB 7.1 多租户在中泰证券中的应用
本文详细介绍了中泰证券在系统国产化改造项目中采用 TiDB 多租户技术的实施过程。文章分析了中泰证券数据库系统现状以及引入 TiDB 资源管控技术的必要性,探讨了 TiDB 多租户的关键特性,并阐述了在实际应用中的具体操作步骤。通过该技术的应用࿰…...

嵌入式-stm32-SR04超声波测距介绍及实战
一:超声波传感器介绍 1.1、SR04超声波测距硬件模块 1.2、SR04的四个IO口 vcc:提供电源5V gnd:接地 Trig:是**发送**声波信号的触发器 Echo:是**接收**回波信号的引脚 当TRIG信号被触发时,传感器会发送一定频率的声波信号,该信号被反射后&am…...

智能优化算法应用:基于白鲸算法3D无线传感器网络(WSN)覆盖优化 - 附代码
智能优化算法应用:基于白鲸算法3D无线传感器网络(WSN)覆盖优化 - 附代码 文章目录 智能优化算法应用:基于白鲸算法3D无线传感器网络(WSN)覆盖优化 - 附代码1.无线传感网络节点模型2.覆盖数学模型及分析3.白鲸算法4.实验参数设定5.算法结果6.参考文献7.MA…...

mac m1芯片 pytorch安装及gpu性能测试
pytorch 使用mac的m1芯片进行模型训练。 #小结:在数据量小和模型参数少,batch_size小时,cpu训练更快(原因:每次训练时数据需要放入GPU中,由于batch_size小。数据放入gpu比模型计算时间还长) 在…...

go 使用 - sync.WaitGroup
使用 - sync.WaitGroup 简介使用注意点 简介 waitgroup 是等待一组并发操作完成得方法。Goroutines对Go来说是独一无二的(尽管其他一些语言有类似的并发原语)。它们不是操作系统线程,它们不完全是绿色的线程(由语言运行时管理的线程)&#x…...
Java Web Day07-08_Layui
1. Layui概念介绍 layui(谐音:类 UI) 是一套开源的 Web UI 解决方案,采用自身经典的模块化规范,并遵循原生 HTML/CSS/JS 的开发方式,极易上手,拿来即用。其风格简约轻盈,而组件优雅丰盈&#x…...
暂时无法办理经营性ICP许可证)
阿里云华北3(张家口)暂时无法办理经营性ICP许可证
阿里云服务器的华北 3(张家口)地域暂时无法办理经营性ICP许可证,如有经营性ICP业务请勿选择此地域。如果需要办理经营性ICP业务的用户,不需要选择华北3(张家口)地域,可以选择华北2(北…...

八种常见顺序存储的算法
目录 1、线性枚举 1)问题描述 2)动图演示 3)示例说明 4)算法描述 5)源码详解 2、前缀和差分 1)问题描述 2)动图演示 3)样例分析 4)算法描述 5)源码…...

Leetcod面试经典150题刷题记录 —— 栈篇
Leetcod面试经典150题刷题记录 —— 栈篇 1. 有效的括号2. 简化路径3. 最小栈4. 逆波兰表达式求值5. 基本计算器 1. 有效的括号 题目链接:有效的括号 - leetcode 题目描述: 给定一个只包括 ( ,),{,},[&…...

【Qt-QThread-QQueue】
Qt编程指南 ■ QThread■ 示例■ QQueue■■■ QThread ■ 示例 #include <QThread> class myThread : public QThread {Q_OBJECT signals...
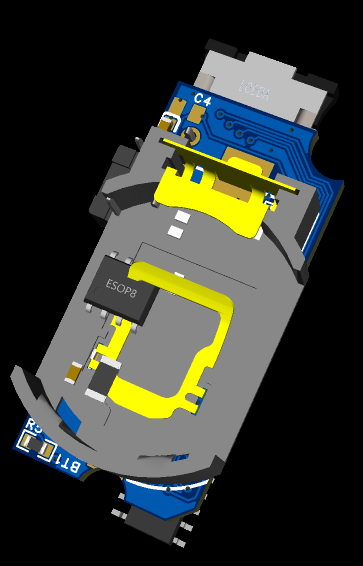
电子握力器改造
toy_hand_game 介绍 消耗体力玩具,使用握力器(Grip Strengthener)控制舵机旋转。 开始设想是控制丝杆电机滑动,两套设备就可以控制两个丝杆电机进行“模拟拔河”,后续发现硬件设计错误,ULN2003不能控制两相四线电机,…...

8k长序列建模,蛋白质语言模型Prot42仅利用目标蛋白序列即可生成高亲和力结合剂
蛋白质结合剂(如抗体、抑制肽)在疾病诊断、成像分析及靶向药物递送等关键场景中发挥着不可替代的作用。传统上,高特异性蛋白质结合剂的开发高度依赖噬菌体展示、定向进化等实验技术,但这类方法普遍面临资源消耗巨大、研发周期冗长…...

iPhone密码忘记了办?iPhoneUnlocker,iPhone解锁工具Aiseesoft iPhone Unlocker 高级注册版分享
平时用 iPhone 的时候,难免会碰到解锁的麻烦事。比如密码忘了、人脸识别 / 指纹识别突然不灵,或者买了二手 iPhone 却被原来的 iCloud 账号锁住,这时候就需要靠谱的解锁工具来帮忙了。Aiseesoft iPhone Unlocker 就是专门解决这些问题的软件&…...

pam_env.so模块配置解析
在PAM(Pluggable Authentication Modules)配置中, /etc/pam.d/su 文件相关配置含义如下: 配置解析 auth required pam_env.so1. 字段分解 字段值说明模块类型auth认证类模块,负责验证用户身份&am…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...
)
WEB3全栈开发——面试专业技能点P2智能合约开发(Solidity)
一、Solidity合约开发 下面是 Solidity 合约开发 的概念、代码示例及讲解,适合用作学习或写简历项目背景说明。 🧠 一、概念简介:Solidity 合约开发 Solidity 是一种专门为 以太坊(Ethereum)平台编写智能合约的高级编…...

BCS 2025|百度副总裁陈洋:智能体在安全领域的应用实践
6月5日,2025全球数字经济大会数字安全主论坛暨北京网络安全大会在国家会议中心隆重开幕。百度副总裁陈洋受邀出席,并作《智能体在安全领域的应用实践》主题演讲,分享了在智能体在安全领域的突破性实践。他指出,百度通过将安全能力…...

用机器学习破解新能源领域的“弃风”难题
音乐发烧友深有体会,玩音乐的本质就是玩电网。火电声音偏暖,水电偏冷,风电偏空旷。至于太阳能发的电,则略显朦胧和单薄。 不知你是否有感觉,近两年家里的音响声音越来越冷,听起来越来越单薄? —…...

【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的“no matching...“系列算法协商失败问题
【SSH疑难排查】轻松解决新版OpenSSH连接旧服务器的"no matching..."系列算法协商失败问题 摘要: 近期,在使用较新版本的OpenSSH客户端连接老旧SSH服务器时,会遇到 "no matching key exchange method found", "n…...

在Mathematica中实现Newton-Raphson迭代的收敛时间算法(一般三次多项式)
考察一般的三次多项式,以r为参数: p[z_, r_] : z^3 (r - 1) z - r; roots[r_] : z /. Solve[p[z, r] 0, z]; 此多项式的根为: 尽管看起来这个多项式是特殊的,其实一般的三次多项式都是可以通过线性变换化为这个形式…...
