Git常用命令复习笔记
1. Git与SVN区别,各自优缺点
Git:
- 分布式,每个参与开发的人的电脑上都有一个完整的仓库,不担心硬盘出问题;
- 在不联网的情况下,照样可以提交到本地仓库,可以查看以往的所有log,等到有网的时候,push到远程即可;
- 非常强大的分支管理功能。
- Git的内容的完整性要优于SVN: GIT的内容存储使用的是SHA-1哈希算法。这能确保代码内容的完整性,确保在遇到磁盘故障和网络问题时降低对版本库的破坏。
SVN:
- 集中式,如果中心服务器出现问题,所有人都不能正常干活,恢复也很麻烦,因为SVN记录的是每次改动的差异,不是完整文件;
- 分支功能没有git强大;
- 速度没有git快,如果有五个分支,是把五个分支的文件全部拷下来;
- 必须联网才能commit。
2. 常用命令
#新增文件的命令:
git add file或者git add
#提交文件的命令:
git commit -m或者git commit -a
#查看工作去状况:
git status -s
#拉取合并远程分支的操作:
git fetch/git merge或者git pull
#查看提交记录命令:
git reflog
#下载远程代码命令:
git clone [url]
#新建一个分支,并切换到该分支:
git checkout -b [branch]
#查看修改的文件:
git status
#添加当前目录的所有文件到暂存区:
git add
#提交暂存区到仓库区:
git commit -m[message]
#取回远程仓库的变化,并与本地分支合并:
git pull [remote]
#上传本地指定分支到远程仓库:git push [remote]
#删除分支:
git branch -d [branch-name]
#删除远程分支:git push origin --delete [branch-name] 或
git branch -dr [remote/branch]
#暂时将未提交的变化移除,稍后再移入
git stash 或
git stash pop

3.提交时发生冲突,冲突是如何产生的吗?你是如何解决的?
开发过程中,我们都有自己的特性分支,所以冲突发生的并不多,但也碰到过。诸如公共类的公共方法,我和别人同时修改同一个文件,他提交后我再提交就会报冲突的错误。
使用命令解决:
- 通过git stash命令,把工作区的修改提交到栈区,目的是保存工作区的修改;
- 通过git pull命令,拉取远程分支上的代码并合并到本地分支,目的是消除冲突;
- 通过git stash pop命令,把保存在栈区的修改部分合并到最新的工作空间中;
如果想撤销提交到索引区的文件,可以通过git reset HEAD file;
3. git fetch和git pull命令之间的区别
简单来说:git fetch branch是把名为branch的远程分支拉取到本地;而git pull branch是在fetch的基础上,把branch分支与当前分支进行merge;因此pull = fetch + merge。
4. git stash命令一般什么情况下会使用它?
解决冲突文件时,会先执行git stash把当前工作区的文件先放入栈中,然后解决冲突;
遇到紧急开发任务但目前任务不能提交时,会先执行git stash,然后进行紧急任务的开发,然后通过git stash pop取出栈区的内容继续开发;
切换分支时,当前工作空间内容不能提交时,会先执行git stash再进行分支切换;
5. git merge和git rebase的区别?
merge会形成一个四边形,产生一个新的commit,就是一次新的提交,把develop分之带过来了;
rebase抛开commidid的变化,就相当于develop从没出现过一样,按顺序在master新提交一遍;
建议使用merge,保留原分支变更,master就是一次一次的merge,gitk命令可以很直观的看到,或平台网页端网络图那里更好看,什么时候合并了一个feture。rebase后看总图,会有很多重复提交;
否则分支的意义是什么?我一直只commit,不push,也不pull,最后push也和rebase后效果一样;
若临时分支会删掉,可以考虑rebase。
6. git cherry-pick有什么作用
命令git cherry-pick可以把branch A的commit复制到branch B上。
在branch B上进行命令操作:
复制单个提交:git cherry-pick commitId
复制多个提交:git cherry-pick commitId1…commitId3
注意:复制多个提交的命令不包含commitId1.
7. github
Github 是一个基于git实现在线代码托管的仓库,向互联网开放,共有仓库免费,建立私有仓库要收费,因为Github的初衷就是为了大家共享自己的劳动成果。
8. gitlab
github和gitlab都是基于git仓库的web开发流程代码托管平台。两者的区别是github有私有仓库和共有仓库,私有仓库一般收费,gitlab打破这种限制,可以免费搭建私有仓库,并且可以部署在自己的服务器上。gitlab不仅有github的功能,还有更多的优秀特性,比如权限设置。一般企业内部软件产品用gitlab是更好的选择,如果是开源产品,一般放在github上。
9. GitHub、GitLab 不同点:
1、GitHub如果使用私有仓库,是需要付费的,GitLab可以在上面搭建私人的免费仓库。
2、GitLab让开发团队对他们的代码仓库拥有更多的控制,相对于GitHub,它有不少的特色:
- (1)允许免费设置仓库权限
- (2)允许用户选择分享一个project的部分代码
- (3)允许用户设置project的获取权限,进一步提升安全性
- (4)可以设置获取到团队整体的改进进度
- (5)通过innersourcing让不在权限范围内的人访问不到该资源
github 是一个基于git实现在线代码托管的仓库,向互联网开放,企业版要收钱。
gitee 即码云,是 oschina 免费给企业用的,不用自己搭建环境。
gitlab 类似 github,一般用于在企业内搭建git私服,要自己搭环境。第一,github针对企业要收费,那当然是不同意,毕竟都想节约资金,那就还能使用gitee,或者gitlab了。
第二,但是码云虽然是免费的,而且不用自己搭环境,但是企业中把项目放在别人的服务器上,始终没有安全感。
第三,因此,衍生出了gitlab,就是用于企业搭私服,而且还是在自己的服务器上。
相关文章:

Git常用命令复习笔记
1. Git与SVN区别,各自优缺点 Git: 分布式,每个参与开发的人的电脑上都有一个完整的仓库,不担心硬盘出问题;在不联网的情况下,照样可以提交到本地仓库,可以查看以往的所有log,等到有…...
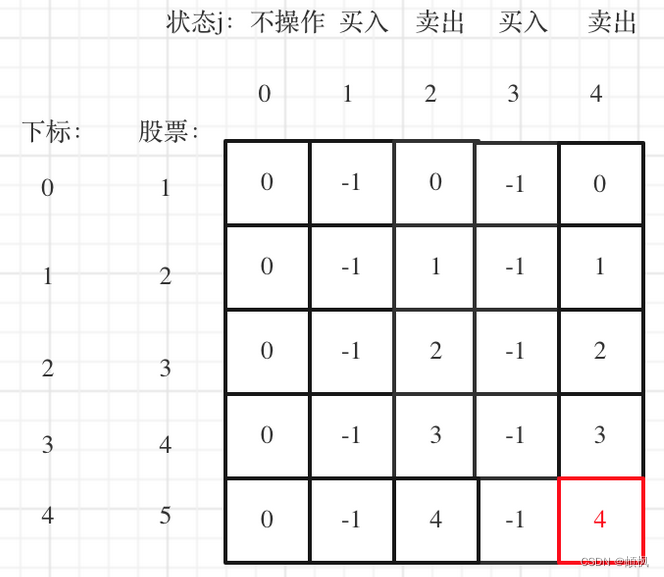
代码随想录算法训练营day49 | 动态规划 123.买卖股票的最佳时机III 188.买卖股票的最佳时机IV
day49123.买卖股票的最佳时机III1.确定dp数组以及下标的含义2.确定递推公式3.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组188.买卖股票的最佳时机IV1.确定dp数组以及下标的含义2.确定递推公式4.dp数组如何初始化4.确定遍历顺序5.举例推导dp数组123.买卖股票的最佳时机III …...
【教学典型案例】14.课程推送页面整理-增加定时功能
目录一:背景介绍1、代码可读性差,结构混乱2、逻辑边界不清晰,封装意识缺乏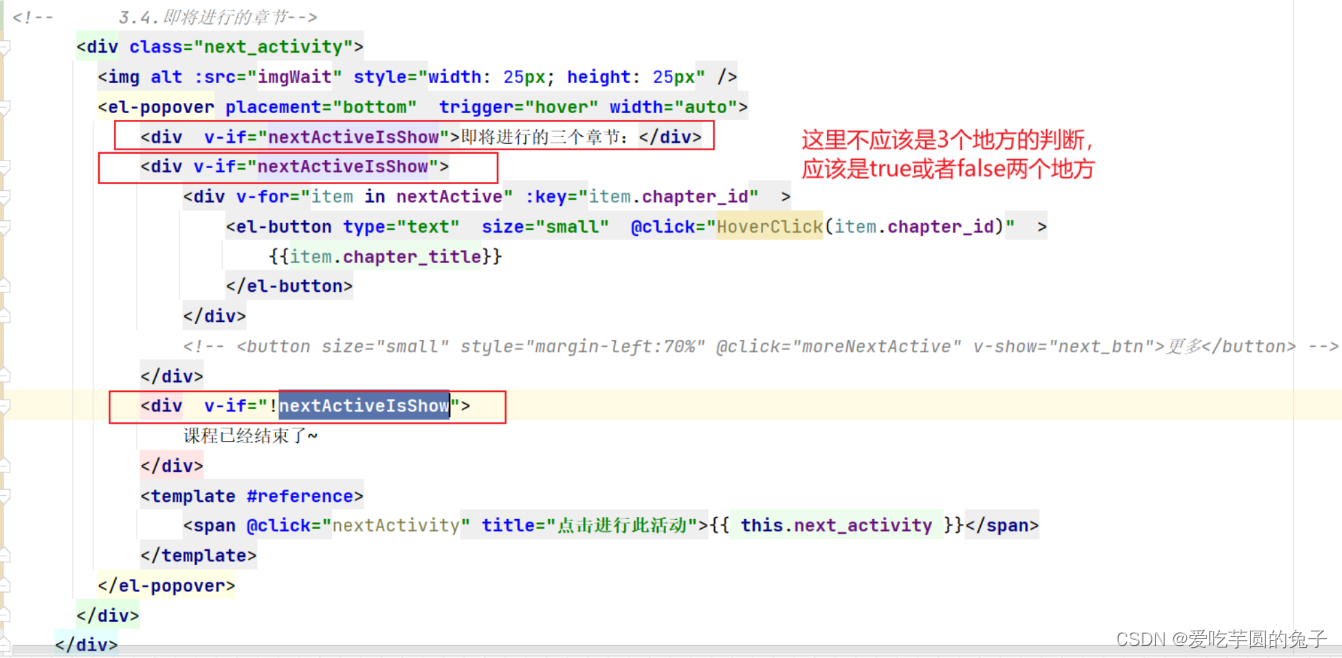3、展示效果不美观二:案例问题分析以及解决过程1、代码可读性…...

【算法基础】DFS BFS 进阶训练
DFS与BFS的基础篇详见:https://blog.csdn.net/m0_51339444/article/details/129301451?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22129301451%22%2C%22source%22%3A%22m0_51339444%22%7D 一、案例分析1 (树的重心 —— D…...

GO语言中的回调函数
0.前言 回调函数是一种在编程中常见的技术,通常在异步编程中使用。简单来说,回调函数是一个被传递给另一个函数的函数,它在该函数的某个时间点被调用,以完成某些特定的操作或任务。 在Go语言中,可以将函数直接作为参…...
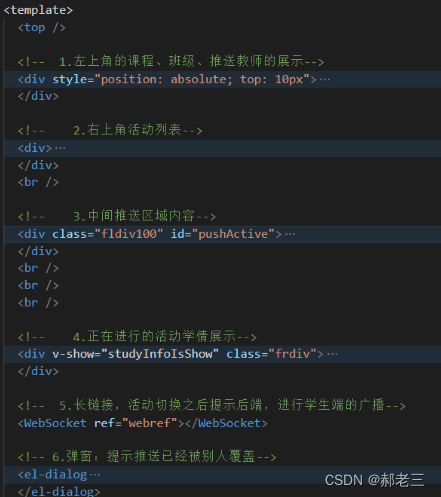
28个案例问题分析---014课程推送页面逻辑整理--vue
一:背景介绍 项目开发过程中,前端出现以下几类问题: 代码结构混乱代码逻辑不清晰页面细节问题 二:问题分析 代码结构混乱问题 <template><top/><div style"position: absolute;top: 10px"><C…...

佛科院单片机原理2——80C51单片机结构
一、程序存储器的入口地址:程序入口地址:0000H外部中断0入口地址:0003H定时器0溢出中断入口地址:000BH外部中断1入口地址:00013H定时器1溢出中断入口地址:001BH串行口中断入口地址:0023H定时器2…...

数据结构与算法_动态顺序表
顺序表是线性表的一种。 线性表是n个具有相同特性的数据元素的有限序列。 逻辑上,它们是线性结构,是一条连续的直线;但是在物理上,它们通常以数组和链式结构存储。 常见的线性表有顺序表、栈、队列、字符串等。 顺序表是用一段…...

逃避浏览器JS检测打开开发者工具
20230304 - 0. 引言 看到一些视频网站之后,想把视频离线下载下来怎么办?直接的方法是通过开发者工具来查看网络流量,一般可以在传输的请求类型中搜索m3u8,然后找到这部分请求,然后利用某些播放器或者下载器直接下载。…...
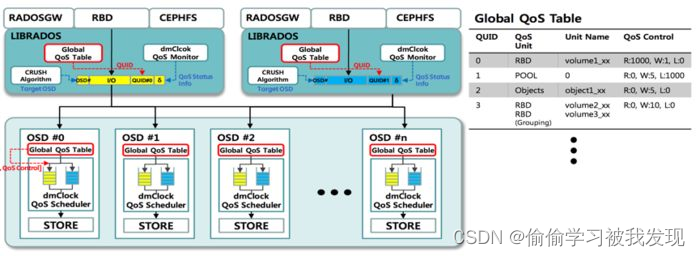
ceph介绍、原理、架构、算法...个人学习记录
前言 之前公司安排出差支援非结构化项目,采用springcloud(redismysql数据冷热处理)s3escephkafka还涉及一些区块链技术等等…,在与大佬的沟通交流下对ceph产生了兴趣,私下学习记录一下;后续工作之余会采用上面相关技术栈手动实现不…...

Spring MVC源码解析——HandlerMapping(处理器映射器)
Sping MVC 源码解析——HandlerMapping处理器映射器1. 什么是HandlerMapping2. HandlerMapping2.1 HandlerMapping初始化2.2 getHandler解析3. getHandlerInternal()子类实现3.1 AbstractUrlHandlerMapping与AbstractHandlerMethodMapping的区别3.2 AbstractUrlHandlerMapping3…...

【Word/word2007】将标题第1章改成第一章
问题:设置多级列表没有其他格式选的解决办法和带来的插入图注解的问题,将标题第1章改成第一章的问题其他方案。 按照百度搜索的方法设置第一章,可以是没有相应的样式可以选。 那就换到编号选项 设置新的编号值 先选是 然就是变得很丑 这时打开…...

NLP预训练模型
Models Corpus RoBERTa: A Robustly Optimized BERT Pretraining Approach 与BERT主要区别在于: large mini-batches 保持总训练tokens数一致,使用更大的学习率、更大的batch size,adam β20.98\beta_20.98β20.98;dynamic ma…...
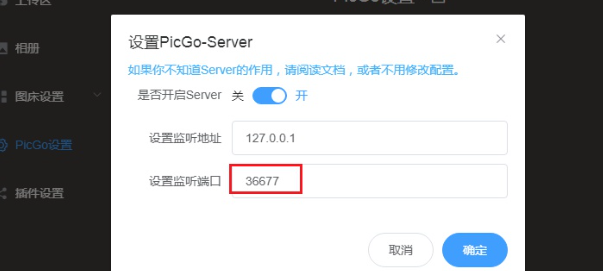
Typora上传文档图片链接失效的问题+PicGo布置图床在Github
文章目录typora图片链接失效原因PicGO开源图床布置先配置Github2.1先创建新仓库、用于存放图片2.2生成一个token,用picGo访问github3.下载picGo,并进行配置3.1 配置v4.1typora图片链接失效原因 因为你是保存在本地的,因此图片是不能访问,可以…...
win10安装oracle
文件放到最后。我的电脑是win11的,因为老师让写下安装笔记,在11上安装的时候没有截屏,所以在虚拟机上重新安装下吧。室友说要把文件夹放到c盘才能打开。我试了下,具体的是要把Oracle11g文件夹放到c盘根目录下。如果解压后不是这个…...
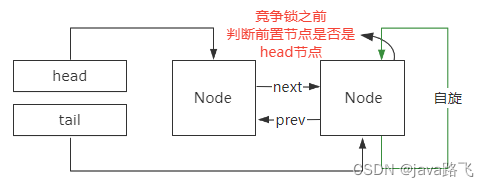
AQS为什么用双向链表?
首先,在AQS中,等待队列是通过Node类来表示的,每个Node节点包含了等待线程的信息以及等待状态。下面是Node类的部分源码:static final class Node {// 等待状态volatile int waitStatus;// 前驱节点volatile Node prev;// 后继节点…...

AtCoder Beginner Contest 292——A-E题讲解
蒟蒻来讲题,还望大家喜。若哪有问题,大家尽可提! Hello, 大家好哇!本初中生蒟蒻讲解一下AtCoder Beginner Contest 292这场比赛的A-E题! A题 原题 Problem Statement You are given a string SSS consisting of lo…...

(蓝桥真题)最长不下降子序列(权值线段树)
样例输入: 5 1 1 4 2 8 5 样例输出: 4 分析:看到这种对其中连续k个数进行修改的我们就应该想到答案是由三部分组成,因为求的是最长不下降子序列,那么我们可以找到一个最合适的断点i,使得答案是由区间[1…...

数据类型及参数传递
1.数据类型 java中的基本数据类型: 数值型: 整数型:byte short long int 浮点型:float double 布尔型: boolean字符串: char java中的引用数据类型: 数组(array) 类(class…...

永春堂1300系统开发|解析永春堂1300模式商城的五大奖项
电商平台竞争越来越激烈,各种营销方式也是层出不穷,其中永春堂1300营销模式,以其无泡沫和自驱动性强等特点风靡一时。在这套模式中,虽然单型价格差异较大,但各种奖励的设计,巧妙的兼顾了平台和所有会员的利…...

微信小程序之bind和catch
这两个呢,都是绑定事件用的,具体使用有些小区别。 官方文档: 事件冒泡处理不同 bind:绑定的事件会向上冒泡,即触发当前组件的事件后,还会继续触发父组件的相同事件。例如,有一个子视图绑定了b…...

【Linux】C语言执行shell指令
在C语言中执行Shell指令 在C语言中,有几种方法可以执行Shell指令: 1. 使用system()函数 这是最简单的方法,包含在stdlib.h头文件中: #include <stdlib.h>int main() {system("ls -l"); // 执行ls -l命令retu…...

微信小程序 - 手机震动
一、界面 <button type"primary" bindtap"shortVibrate">短震动</button> <button type"primary" bindtap"longVibrate">长震动</button> 二、js逻辑代码 注:文档 https://developers.weixin.qq…...

Cinnamon修改面板小工具图标
Cinnamon开始菜单-CSDN博客 设置模块都是做好的,比GNOME简单得多! 在 applet.js 里增加 const Settings imports.ui.settings;this.settings new Settings.AppletSettings(this, HTYMenusonichy, instance_id); this.settings.bind(menu-icon, menu…...

大学生职业发展与就业创业指导教学评价
这里是引用 作为软工2203/2204班的学生,我们非常感谢您在《大学生职业发展与就业创业指导》课程中的悉心教导。这门课程对我们即将面临实习和就业的工科学生来说至关重要,而您认真负责的教学态度,让课程的每一部分都充满了实用价值。 尤其让我…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...

群晖NAS如何在虚拟机创建飞牛NAS
套件中心下载安装Virtual Machine Manager 创建虚拟机 配置虚拟机 飞牛官网下载 https://iso.liveupdate.fnnas.com/x86_64/trim/fnos-0.9.2-863.iso 群晖NAS如何在虚拟机创建飞牛NAS - 个人信息分享...

BLEU评分:机器翻译质量评估的黄金标准
BLEU评分:机器翻译质量评估的黄金标准 1. 引言 在自然语言处理(NLP)领域,衡量一个机器翻译模型的性能至关重要。BLEU (Bilingual Evaluation Understudy) 作为一种自动化评估指标,自2002年由IBM的Kishore Papineni等人提出以来,…...

消息队列系统设计与实践全解析
文章目录 🚀 消息队列系统设计与实践全解析🔍 一、消息队列选型1.1 业务场景匹配矩阵1.2 吞吐量/延迟/可靠性权衡💡 权衡决策框架 1.3 运维复杂度评估🔧 运维成本降低策略 🏗️ 二、典型架构设计2.1 分布式事务最终一致…...
