差分进化算法求解基于移动边缘计算 (MEC) 的无线区块链网络的联合挖矿决策和资源分配(提供MATLAB代码)
一、优化模型介绍
在所研究的区块链网络中,优化的变量为:挖矿决策(即 m)和资源分配(即 p 和 f),目标函数是使所有矿工的总利润最大化。问题可以表述为:
max m , p , f F miner = ∑ i ∈ N ′ F i miner s.t. C 1 : m i ∈ { 0 , 1 } , ∀ i ∈ N C 2 : p min ≤ p i ≤ p max , ∀ i ∈ N ′ C 3 : f min ≤ f i ≤ f max , ∀ i ∈ N ′ C 4 : ∑ i ∈ N ′ f i ≤ f total C 5 : F M S P ≥ 0 C 6 : T i t + T i m + T i o ≤ T i max , ∀ i ∈ N ′ \begin{aligned} \max _{\mathbf{m}, \mathbf{p}, \mathbf{f}} & F^{\text {miner }}=\sum_{i \in \mathcal{N}^{\prime}} F_{i}^{\text {miner }} \\ \text { s.t. } & C 1: m_{i} \in\{0,1\}, \forall i \in \mathcal{N} \\ & C 2: p^{\min } \leq p_{i} \leq p^{\max }, \forall i \in \mathcal{N}^{\prime} \\ & C 3: f^{\min } \leq f_{i} \leq f^{\max }, \forall i \in \mathcal{N}^{\prime} \\ & C 4: \sum_{i \in \mathcal{N}^{\prime}} f_{i} \leq f^{\text {total }} \\ & C 5: F^{M S P} \geq 0 \\ & C 6: T_{i}^{t}+T_{i}^{m}+T_{i}^{o} \leq T_{i}^{\max }, \forall i \in \mathcal{N}^{\prime} \end{aligned} m,p,fmax s.t. Fminer =i∈N′∑Fiminer C1:mi∈{0,1},∀i∈NC2:pmin≤pi≤pmax,∀i∈N′C3:fmin≤fi≤fmax,∀i∈N′C4:i∈N′∑fi≤ftotal C5:FMSP≥0C6:Tit+Tim+Tio≤Timax,∀i∈N′
其中:
C1表示每个矿工可以决定是否参与挖矿;
C2 指定分配给每个参与矿机的最小和最大传输功率;
C3 表示分配给每个参与矿工的最小和最大计算资源;
C4表示分配给参与矿机的总计算资源不能超过MEC服务器的总容量;
C5保证MSP的利润不小于0;
C6 规定卸载、挖掘和传播步骤的总时间不能超过最长时间约束。
在所研究的区块链网络中,我们假设 IoTD 是同质的,并且每个 IoTD 都具有相同的传输功率范围和相同的计算资源范围。
上式中:
F i m i n e r = ( w + α D i ) P i m ( 1 − P i o ) − c 1 E i t − c 2 f i , ∀ i ∈ N ′ R i = B log 2 ( 1 + p i H i σ 2 + ∑ j ∈ N ′ \ i m j p j H j ) , ∀ i ∈ N ′ T i t = D i R i , ∀ i ∈ N ′ T i m = D i X i f i , ∀ i ∈ N ′ E i m = k 1 f i 3 T i m , ∀ i ∈ N ′ P i m = k 2 T i m , ∀ i ∈ N ′ F M S P = ∑ i ∈ N ′ ( c 2 f i − c 3 E i m ) − c 3 E 0 P i o = 1 − e − λ ( T i o + T i s ) = 1 − e − λ ( z D i + T i t ) , ∀ i ∈ N ′ F_i^{miner}=(w+\alpha D_i)P_i^m(1-P_i^o)-c_1E_i^t-c_2f_i,\forall i\in\mathcal{N'}\\R_{i}=B \log _{2}\left(1+\frac{p_{i} H_{i}}{\sigma^{2}+\sum_{j \in \mathcal{N}^{\prime} \backslash i} m_{j} p_{j} H_{j}}\right), \forall i \in \mathcal{N}^{\prime}\\T_{i}^{t}=\frac{D_{i}}{R_{i}},\forall i\in\mathcal{N}^{\prime}\\T_{i}^{m}=\frac{D_{i}X_{i}}{f_{i}},\forall i\in\mathcal{N}'\\E_i^m=k_1f_i^3T_i^m,\forall i\in\mathcal{N}'\\P_i^m=\frac{k_2}{T_i^m},\forall i\in\mathcal{N}^{\prime}\\F^{MSP}=\sum_{i\in\mathcal{N}^{\prime}}\left(c_2f_i-c_3E_i^m\right)-c_3E_0\\\begin{aligned} P_{i}^{o}& =1-e^{-\lambda(T_{i}^{o}+T_{i}^{s})} \\ &=1-e^{-\lambda(zD_{i}+T_{i}^{t})},\forall i\in\mathcal{N}^{\prime} \end{aligned} Fiminer=(w+αDi)Pim(1−Pio)−c1Eit−c2fi,∀i∈N′Ri=Blog2(1+σ2+∑j∈N′\imjpjHjpiHi),∀i∈N′Tit=RiDi,∀i∈N′Tim=fiDiXi,∀i∈N′Eim=k1fi3Tim,∀i∈N′Pim=Timk2,∀i∈N′FMSP=i∈N′∑(c2fi−c3Eim)−c3E0Pio=1−e−λ(Tio+Tis)=1−e−λ(zDi+Tit),∀i∈N′
二、差分进化算法求解
2.1部分代码
close all
clear
clc
dbstop if all error
NP = 100;%矿工数量
para = parametersetting(NP);
para.MaxFEs =5000;%最大迭代次数
Result=Compute(NP,para);
figure(1)
plot(Result.FitCurve,'r-','linewidth',2)
xlabel('FEs')
ylabel('Token')
figure(2)
plot(Result.ConCurve,'g-','linewidth',2)
xlabel('FEs')
ylabel('Con')2.2部分结果
当矿工数量为100时:所有矿工的利润随迭代次数的变化如下图所示
 算法得到的资源分配:
算法得到的资源分配:
1.99763301712028 0.222528597636855
1.98480090600989 0.232003797981878
1.99810737020089 0.516878075461127
1.99450954175327 0.121004799048830
1.98894335292950 0.457573161395314
1.98141441375851 0.764801153373885
1.99123792611056 0.0618336115864624
1.99957268156257 0.121004799048830
1.99869990696838 0.0545812896345451
1.99958167059988 0.555322442727203
1.99842776886770 0.0425674932800246
1.99782546212753 0.556999423219330
1.99781790486039 0.196587806899822
1.99507786088204 0.115226131066544
1.99052235611421 0.245674972808444
1.99670598640193 0.0505531222716088
1.99482731112569 0.570493296084591
1.99736278961552 0.483094177861634
1.98894335292950 0.262561711571175
1.98784689496156 0.0324778719744346
1.98851683245790 0.171964220456218
1.98796386190418 0.110054645825889
1.98418972990049 0.0724358226961023
1.99516235341290 0.0341179120870288
1.99873738363101 0.489382783726158
1.99697974388302 0.0173712437086769
1.98964833679332 0.0320026913839283
1.99751719786278 0.147890074497164
1.99751719786278 0.434936315273999
1.99748331769841 0.232003797981878
1.99960825876476 0.483665232586750
1.99763301712028 0.631745087572258
1.99703599779628 0.358292746434059
1.99528222092061 0.514944354258863
1.99655084169003 0.753834027257007
1.99842776886770 0.940560567187612
1.99836116767571 0.221230559879615
1.99981576341436 0.184249732087410
1.99836116767571 0.0324778719744346
1.99654201611710 0.335915952413277
1.99237903891650 0.155001423906853
1.99760611708088 0.375017552592607
1.99978704361437 0.561786832194378
1.98578574172372 0.0236239899979008
1.99866761178096 0.0324778719744346
1.99763301712028 0.472369465588862
1.99721838438050 0.700915679954801
1.99428564716577 0.157199586550231
1.99655135483398 0.105209390328771
1.94788362094720 0.0258755419701254
1.99449453062393 0.132251896484895
1.99700992290778 0.0898397719008559
1.99965518095321 0.596537124037070
1.99278786910748 0.0256042543513514
1.99957848431148 0.894961847587823
1.99175299365895 0.0890674637434230
1.99750797157559 0.607592532504797
1.99748331769841 0.0724358226961023
1.99260527116064 0.631745087572258
1.99928439965780 0.127930497832236
1.99817708666189 0.104282160660561
1.99421206141539 0.803656147079701
1.98359960108601 0.118868109287597
1.99899700099444 0.518357001275729
1.99528222092061 0.0324778719744346
1.99877098644022 0.665529673319171
1.99763301712028 0.334090268607101
1.99860560539076 0.0866379799536027
1.99979684848517 0.377299990245342
1.99855631180132 0.389679849807951
1.99731236573268 0.434936315273999
1.99696360320736 0.570493296084591
1.99993018378939 0.391296247028955
1.99965327995029 0.287460195344814
1.99979684848517 0.450997212108626
1.99751719786278 0.287460195344814
1.99763301712028 0.155001423906853
1.99783983352391 0.103569288167448
1.99654201611710 0.127930497832236
1.98747116264687 0.0330088002325308
1.99655135483398 0.0797018166113099
1.99108222250111 0.0866379799536027
1.99718273730151 0.662248213795699
1.99869990696838 0.191058236556442
1.99652919147221 0.215505887700011
1.99459957647011 0.140056664895674
1.99806054285466 0.120547231379614
1.98593862830166 0.0916486389328984
1.97931641143295 0.462734428071515
1.99855631180132 0.101120011114003
1.99421206141539 0.258443908859530
1.99781790486039 0.543516910843497
1.99720522726900 0.0737173931186571
1.98303440848516 0.152622777636722
1.99900862513681 0.674526132004626
1.99866761178096 0.358292746434059
1.99783983352391 0.491305146804456
1.99960825876476 0.122579254402338
1.96710953562570 0.0513811784835662
1.99842776886770 0.0112006869294710
三、完整MATLAB代码
相关文章:

差分进化算法求解基于移动边缘计算 (MEC) 的无线区块链网络的联合挖矿决策和资源分配(提供MATLAB代码)
一、优化模型介绍 在所研究的区块链网络中,优化的变量为:挖矿决策(即 m)和资源分配(即 p 和 f),目标函数是使所有矿工的总利润最大化。问题可以表述为: max m , p , f F miner …...

Tomcat Notes: Web Security, HTTPS In Tomcat
This is a personal study notes of Apache Tomcat. Below are main reference material. - YouTube Apache Tomcat Full Tutorial,owed by Alpha Brains Courses. https://www.youtube.com/watch?vrElJIPRw5iM&t801s 1、Overview2、Two Levels Of Web Securi…...

智能小程序登陆能力开发文档及示例代码
小程序登录 涂鸦官方提供了登录能力,开发者可以通过相关 API 获取 App 的用户身份标识,快速的建立小程序内的用户体系。 登录流程 说明 需要调用 ty.login() 获取 临时登录凭证 code,并将 code 传到开发者服务器开发者服务器调用涂鸦云开发…...
常见の算法
前言本文主要使用Java 什么,是快乐星球#¥%……什么是算法? 算法是一组完成任务的指令。任何代码片段都可视为算法,但我们主要介绍常见算法 一、引入——二分查找 二分查找是一种算法,其输入是一个有序的元素列表。如…...

openssl3.2/test/certs - 041 - 1024-bit leaf key
文章目录 openssl3.2/test/certs - 041 - 1024-bit leaf key概述笔记END openssl3.2/test/certs - 041 - 1024-bit leaf key 概述 openssl3.2 - 官方demo学习 - test - certs 笔记 /*! * \file D:\my_dev\my_local_git_prj\study\openSSL\test_certs\041\my_openssl_linux_…...

「创新引领未来」科东软件荣获第十二届中国创新创业大赛(广东·广州赛区)优胜奖
近日,广州市科学技术局公布第十二届中国创新创业大赛(广东广州赛区)暨2023年广州科技创新创业大赛常规赛拟获奖企业名单。科东软件凭借国产化技术创新优势、强大的应用场景落地能力和丰富的行业解决方案,荣获第十二届中国创新创业…...
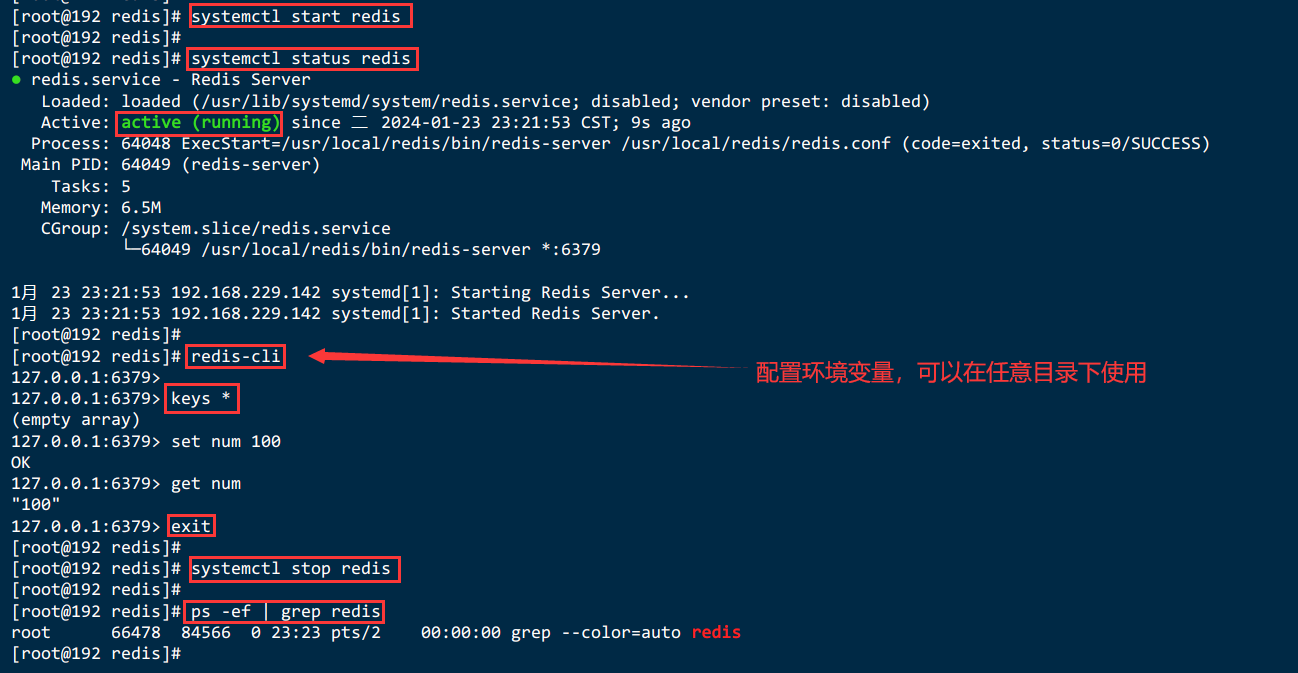
Linux下安装 Redis7
Linux下安装 Redis7 三、Linux下安装 Redis7【redis-7.2.4.tar.gz】3.1.下载redis的安装包3.1.1.手动下载Redis压缩包并上传【redis-7.2.4.tar.gz】3.1.2.wget工具下载redis-7.2.4.tar.gz 3.2.将安装包进行解压缩3.3.进入redis的安装包3.4.检查是否有gcc 环境3.5.编译和安装并指…...

spire.doc合并word文档
文章目录 spire.doc合并word文档1. 引入maven依赖2. 需要合并的word3. 合并文档代码4. 合并结果 spire.doc合并word文档 1. 引入maven依赖 <repositories><repository><id>com.e-iceblue</id><name>e-iceblue</name><url>https://r…...

蓝桥杯官网填空题(01串的熵)
问题描述 答案提交 这是一道结果填空的题, 你只需要算出结果后提交即可。本题的结果为一 个整数, 在提交答案时只填写这个整数, 填写多余的内容将无法得分。 import java.util.*;public class Main {public static void main(String[] args) {for(double zero1;zero<2333…...

【CodeTop】TOP 100 刷题 51-60
文章目录 51. 缺失的第一个正数题目描述代码与解题思路 52. 训练计划 II题目描述代码与解题思路 53. 子集题目描述代码与解题思路 54. 最小覆盖子串题目描述代码与解题思路 55. 从前序与中序遍历序列构造二叉树题目描述代码与解题思路 56. 零钱兑换题目描述代码与解题思路 57. …...

k8s的图形化工具---rancher
rancher是一个开源的企业级多集群的k8s管理平台。 rancher和k8s的区别:都是为了容器的调度和编排系统。但是rancher不仅可以调度还可以管理整个k8s集群。 rancher自带监控(普罗米修斯) 实验部署 master01 20.0.0.32 node01 20.0.0.34 node02 20.0.0.35 test …...
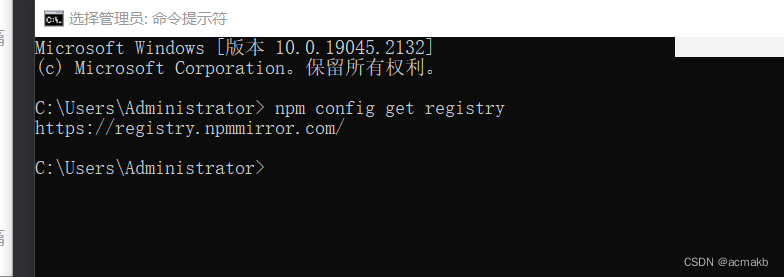
npm安装卡住问题(最新版)
npm安装卡住问题(最新版) 背景: 最近这两天用npm安装一些包的时候,发现一直卡住: 报错: idealTree:npm: sill idealTree buildDeps之前能用的现在不能用了,我一想,是不是源头的问题,还真是…...
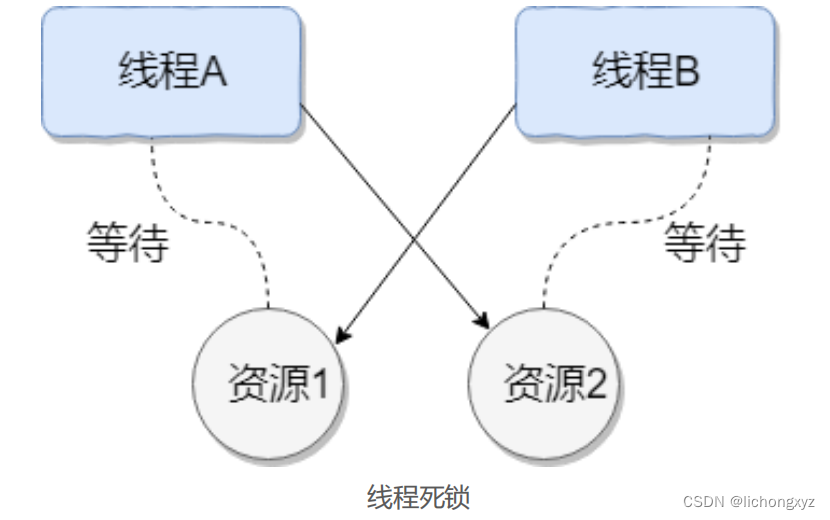
什么是线程死锁
死锁是指两个或两个以上的进程(线程)在执行过程中,由于竞争资 源或者由于彼此通信而造成的一种阻塞的现象,若无外力作用,它们都将无法推 进下去。此时称系统处于死锁状态或系统产生了死锁,这些永远在互相…...
Django从入门到精通(二)
目录 三、视图 3.1、文件or文件夹 3.2、相对和绝对导入urls 3.3、视图参数requests 3.4、返回值 3.5、响应头 3.6、FBV和CBV FBV 四、静态资源 4.1、静态文件 4.2、媒体文件 五、模板 5.1、寻找html模板 5.2、模板处理的本质 5.3、常见模板语法 5.4、内置模板函…...

建筑物防雷检测安全接地应用解决方案
雷电是一种自然现象,具有极高的电压和电流,对建筑物及其内部设备、人员和财产可能造成严重的危害,如火灾、爆炸、电击、电磁干扰等。因此,建筑物必须采取有效的防雷措施,以保障建筑物的安全和可靠运行。建筑物防雷检测…...
支付宝小程序开发踩坑笔记(支付宝、学习强国小程序)
1、接口请求安卓端回调 success,IOS 端回调 fail 原因:dataType 设置不对,默认是 json 格式,对返回数据会进行 json 解析,如果解析失败,就会回调 fail 。加密传输一般是 text 格式。 2、input 禁止输入空格…...
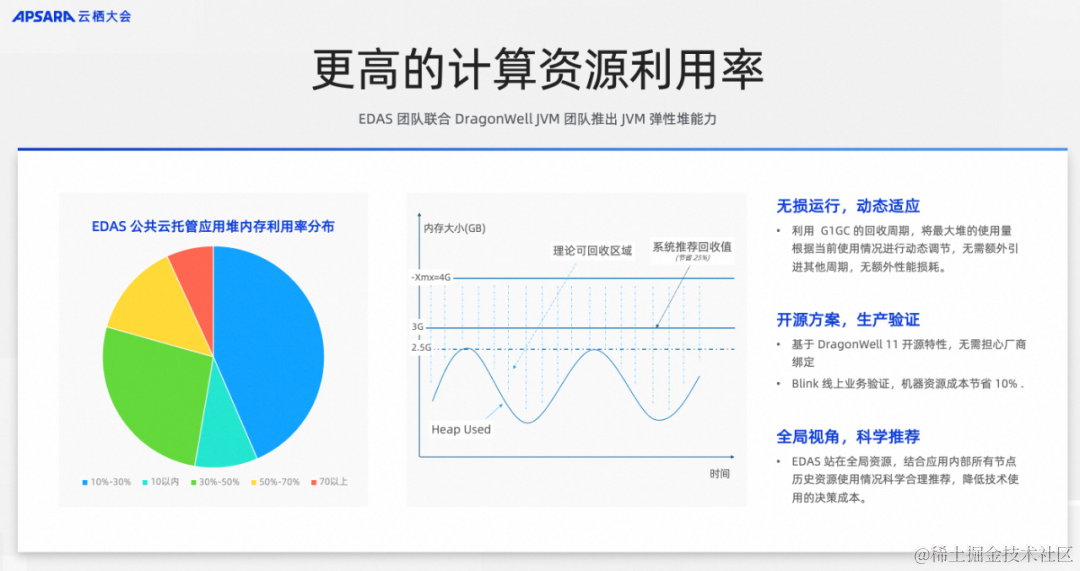
如何降低微服务复杂度丨云栖大会微服务主题分享实录
作者:谢吉宝 本文整理自阿里云资深技术专家、中间件负责人谢吉宝在2023云栖大会《极简微服务模式,降低微服务复杂度的最佳实践》的分享 2023 云栖大会现场 当面临复杂的挑战时,"分而治之"的方法往往能取得显著的效果。微服务架构…...

openresty 安装, nginx与 openresty
openresty VS nginx Nginx 是一款高性能的 Web 服务器和反向代理服务器,具备基础的功能如HTTP服务、负载均衡、反向代理以及动静分离等。它是许多互联网应用的核心组件,因其模块化和可扩展的设计而受到欢迎。1 OpenResty 是基于 Nginx 的 Web 平台&…...

puppeteer实现截图
Window服务器说明 1.在本地安装 puppeteer 先创建一个本地文件夹puppeteer,我的地址D:\common_workspace\puppeteer 然后使用cmd打开这个文件夹所在位置,再执行如下两条命令即可。 npm install -g cnpm --registryhttps://registry.npm.taobao.orgcnpm …...
【2024Java面试突击】并发编程、线程池面试实战
前言 最近在更新面试突击专栏,我把每一篇将字数都尽量控制在 2000 字以内,可能在文章里边写的没有那么细致,主要是提供一些 问题 以及 回答的思路 ,以及 面试中可能忽略的漏洞 ,所以在看完文章之后,如果自…...

边缘计算医疗风险自查APP开发方案
核心目标:在便携设备(智能手表/家用检测仪)部署轻量化疾病预测模型,实现低延迟、隐私安全的实时健康风险评估。 一、技术架构设计 #mermaid-svg-iuNaeeLK2YoFKfao {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg…...

2024年赣州旅游投资集团社会招聘笔试真
2024年赣州旅游投资集团社会招聘笔试真 题 ( 满 分 1 0 0 分 时 间 1 2 0 分 钟 ) 一、单选题(每题只有一个正确答案,答错、不答或多答均不得分) 1.纪要的特点不包括()。 A.概括重点 B.指导传达 C. 客观纪实 D.有言必录 【答案】: D 2.1864年,()预言了电磁波的存在,并指出…...

el-switch文字内置
el-switch文字内置 效果 vue <div style"color:#ffffff;font-size:14px;float:left;margin-bottom:5px;margin-right:5px;">自动加载</div> <el-switch v-model"value" active-color"#3E99FB" inactive-color"#DCDFE6"…...

(二)原型模式
原型的功能是将一个已经存在的对象作为源目标,其余对象都是通过这个源目标创建。发挥复制的作用就是原型模式的核心思想。 一、源型模式的定义 原型模式是指第二次创建对象可以通过复制已经存在的原型对象来实现,忽略对象创建过程中的其它细节。 📌 核心特点: 避免重复初…...
的原因分类及对应排查方案)
JVM暂停(Stop-The-World,STW)的原因分类及对应排查方案
JVM暂停(Stop-The-World,STW)的完整原因分类及对应排查方案,结合JVM运行机制和常见故障场景整理而成: 一、GC相关暂停 1. 安全点(Safepoint)阻塞 现象:JVM暂停但无GC日志,日志显示No GCs detected。原因:JVM等待所有线程进入安全点(如…...
)
【HarmonyOS 5 开发速记】如何获取用户信息(头像/昵称/手机号)
1.获取 authorizationCode: 2.利用 authorizationCode 获取 accessToken:文档中心 3.获取手机:文档中心 4.获取昵称头像:文档中心 首先创建 request 若要获取手机号,scope必填 phone,permissions 必填 …...

Mac下Android Studio扫描根目录卡死问题记录
环境信息 操作系统: macOS 15.5 (Apple M2芯片)Android Studio版本: Meerkat Feature Drop | 2024.3.2 Patch 1 (Build #AI-243.26053.27.2432.13536105, 2025年5月22日构建) 问题现象 在项目开发过程中,提示一个依赖外部头文件的cpp源文件需要同步,点…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...

Xen Server服务器释放磁盘空间
disk.sh #!/bin/bashcd /run/sr-mount/e54f0646-ae11-0457-b64f-eba4673b824c # 全部虚拟机物理磁盘文件存储 a$(ls -l | awk {print $NF} | cut -d. -f1) # 使用中的虚拟机物理磁盘文件 b$(xe vm-disk-list --multiple | grep uuid | awk {print $NF})printf "%s\n"…...

push [特殊字符] present
push 🆚 present 前言present和dismiss特点代码演示 push和pop特点代码演示 前言 在 iOS 开发中,push 和 present 是两种不同的视图控制器切换方式,它们有着显著的区别。 present和dismiss 特点 在当前控制器上方新建视图层级需要手动调用…...
