基于RMF的信贷风控标签客户分层管理
根据美国 数据库营销研究所Arthur Hughes的研究,客户数据库中有3个神奇的要素,这3个要素构成了数据分析最好的指标:最近一次消费 (Recency)、消费频率(Frequency)、消费金额 (Monetary)。这就是RMF模型,RMF模型是用户分层的重要手段,是用于分析当前用户价值和客户潜在价值的重要工具。核心就是通过搭建用户标签体系,进行用户分层,实现对用户有针对性的精细化运营。

▍基于RMF的信贷风控用户标签体系建设
用户画像是了解你的客户的有效方式,常见的用户画像包括但不限于年龄、性别、手机归属地、学历、职业、婚姻状态、机型、银行卡、消费、app偏好等。互金用户还有新老户比例、额度、息费、多头程度、借款次数、借款金额、展期次数、逾期次数、逾期升期等。
还款能力(偿债收入比=收入水平与负债水平、资产水平),还款意愿(最低还款情况和提前还款、历史逾期还款等情况),多头借贷意向(近期查询机构数和查询次数)。基于RMF模型选取这三个维度作为基础,搭建客群风险标签,刻画客户画像,进行客户分层管理,拦截高风险客户。
还款能力作为M(消费金额),还款意愿作为R(最近一次消费),多头借贷作为F(消费频率),基于客群的还款能力、还款意愿、多头借贷3维度标签建立客群分层管理。
▍基于新风险标签的二级指标建设
还款能力:收入水平(信用卡额度、信用卡账单、房贷数据、公积金数据)、负债水平(征信月还款负债)、资产水平(车房股票基金)、消费能力水平、偿债收入比指标。
还款意愿:借款频率、还款准时性、借款金额、最低还款和提前还款、历史逾期还款行为习惯等情况。还有就是客群违约成本大小(个人资质,可通过学历、职位、家庭地位、单位性质等维度)
多头借贷:客群最近7天、1个月、3个月、6个月、12个月、18个月、24个月的(各类平台)借贷(贷款/贷记卡)查询次数、机构数、金额。安装借贷App的数量、平台类别、安装时间等数据的获取和使用。还有就是占比,例如最近7天的多头借贷总次数 / 最近1个月的多头借贷总次数以此可判断借款人的时间维度上的借贷行为分布。该比值越大,代表最近一个月的申贷记录集中在最近7天,借款人最近资金短缺。还有近*月贷款成功笔数/近*月查询次数等借款通过率指标,来判断客群多头借贷资质和需求,该值越低,代表客群资质越差。最近1个月的银行信用卡中心借贷次数 / 最近1个月的多头借贷总次数以此可判断借款人在机构维度的借贷行为分布。数值越大,可认为越趋于正面。通常银行客群较好,互金客群较差。
▍计算3维矩阵的得分
基于二级指标体系,分别计算出还款能力指数、还款意愿指数、多头借贷指数。还款能力指数是越大,客户越优质。还款意愿指数是越大,客户越优质。多头借贷指数是越大,客户越差。每一个维度分为高中低三个等级,客群一共可以细分为9个客群。可基于因子得分模型,结合客群好坏标签Y字段,来进行监督训练,得到二级指标的系数参数。类似分箱和评分卡的机制,对这三个维度进行打分,然后结合多维矩阵划分客群,进行有效管理。
相关文章:

基于RMF的信贷风控标签客户分层管理
根据美国 数据库营销研究所Arthur Hughes的研究,客户数据库中有3个神奇的要素,这3个要素构成了数据分析最好的指标:最近一次消费 (Recency)、消费频率(Frequency)、消费金额 (Monetary)。这就是RMF模型,RMF模型是用户分层的重要手…...

【MySQL】如何通过DDL去创建和修改员工信息表
🌈个人主页: Aileen_0v0 🔥热门专栏: 华为鸿蒙系统学习|计算机网络|数据结构与算法 💫个人格言:“没有罗马,那就自己创造罗马~” #mermaid-svg-fmKISDBsFq74ab2Z {font-family:"trebuchet ms",verdana,arial,sans-serif;font-siz…...
Spring 事务原理一
从本篇博客开始,我们将梳理Spring事务相关的知识点。在开始前,想先给自己定一个目标:通过此次梳理要完全理解事务的基本概念及Spring实现事务的基本原理。为实现这个目标我想按以下几个步骤进行: 讲解事务中的一些基本概念使用Sp…...

creo草绘3个实例学习笔记
creo草绘3个实例 文章目录 creo草绘3个实例草绘01草绘02草绘03 草绘01 草绘02 草绘03...

Modern C++ std::move的实现原理
前言 有一节我们分析了std::bind的实现原理,本节稍作休息分析一个比较简单的std::move 原理 std::move的原理太简单了,一句话:就是把传进来的参数强转为右值引用类型。作用为调用移动构造函数,或移动赋值函数。下面通过例子和代…...

爬虫工作量由小到大的思维转变---<第四十章 Scrapy Redis 实现IP代理池管理的最佳实践>
前言: 本篇是要结合上篇一起看的姊妹篇:爬虫工作量由小到大的思维转变---<第三十九章 Scrapy-redis 常用的那个RetryMiddleware>-CSDN博客 IP代理池的管理对于确保爬虫的稳定性和数据抓取的匿名性至关重要。围绕Scrapy-Redis框架和一个具体的IP代理池中…...

C# 实现 XOR 密码
XOR密码(异或密码)是一种简单的加密算法,它使用异或(XOR)操作来对明文和密钥进行加密和解密。 异或操作是一种位运算,它对两个二进制数的对应位进行比较,如果两个位相同(都为0或都为…...
【Web前端开发基础】CSS3之空间转换和动画
CSS3之空间转换和动画 目录 CSS3之空间转换和动画一、空间转换1.1 概述1.2 3D转换常用的属性1.3 3D转换:translate3d(位移)1.4 3D转换:perspective(视角)1.5 3D转换:rotate3d(旋转&a…...
)
Go实现一个简单的烟花秀效果(附带源码)
在 Go 语言中,要实现烟花秀效果可以使用 github.com/fogleman/gg 包进行绘图。以下是一个简单的例子: 首先,确保你已经安装了(有时候需要梯子才可以安装) github.com/fogleman/gg 包: go get -u github.c…...
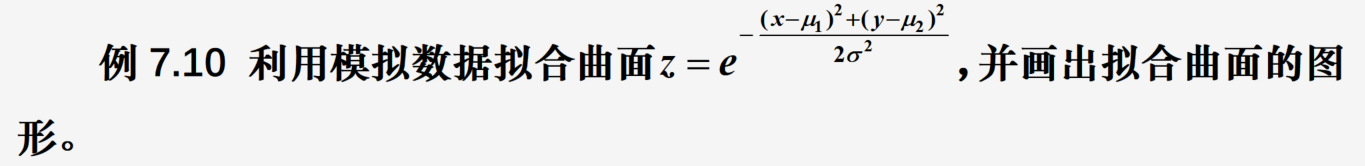
【数学建模】插值与拟合
文章目录 插值插值方法用Python解决插值问题 拟合最小二乘拟合数据拟合的Python实现 适用情况 处理由试验、测量得到的大量数据或一些过于复杂而不便于计算的函数表达式时,构造一个简单函数作为要考察数据或复杂函数的近似 定义 给定一组数据,需要确定满…...
全卷积网络:革新图像分析
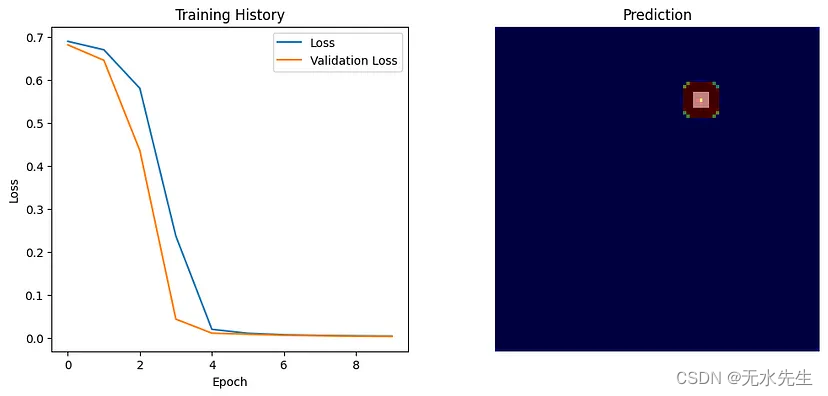
一、介绍 全卷积网络(FCN)的出现标志着计算机视觉领域的一个重要里程碑,特别是在涉及图像分析的任务中。本文深入探讨了 FCN 的概念、它们的架构、它们与传统卷积神经网络 (CNN) 的区别以及它们在各个领域的应用。 就像…...

ubuntu20.04 格式化 硬盘 扩展硬盘GParted
如何在 Ubuntu 22.04 LTS 上安装分区编辑器 GParted?_gparted安装-CSDN博客 sudo apt install gparted 步骤5:启动GParted 安装完成后,您可以在应用程序菜单中找到GParted。点击它以启动分区编辑器。 通过以上步骤,您可以在Ubun…...

docker的资源限制(cgroup)
前瞻 Docker 通过 Cgroup 来控制容器使用的资源配额,包括 CPU、内存、磁盘三大方面, 基本覆盖了常见的资源配额和使用量控制。 Cgroup 是 ControlGroups 的缩写,是 Linux 内核提供的一种可以限制、记录、隔离进程组所使用的物理资源(如 CPU、…...

ChatGPT与文心一言:应用示例与体验比较
ChatGPT 和文心一言哪个更好用? 为了更好地感受ChatGPT和文心一言这两款AI助手如何在实际运用中竞相辉映,我将提供一些典型的应用示例。这些示例都取自真实的用户体验,以帮助解释这两种工具如何让日常生活或工作变得更加轻松。 ChatGPT Ch…...
紫光展锐T760_芯片性能介绍_展锐T760安卓核心板定制
展锐T760核心板是一款基于国产5G芯片的智能模块,采用紫光展锐T760制程工艺为台积电6nm工艺,支持工艺具有出色的能效表现。其采用主流的44架构的八核设计,包括4颗2.2GHz A76核心和4颗A55核心设计,内存单元板载可达8GB Ram256GB ROM…...

从动力系统研究看当今数学界
6.3... Milnor’s definition of “attractors” which has been criticized above by us). The work of [KSS2] of asserting the existence of “nice open set” of Ω(p.148) would be likely not verified, for example we think the first sentence “… since f is nont…...
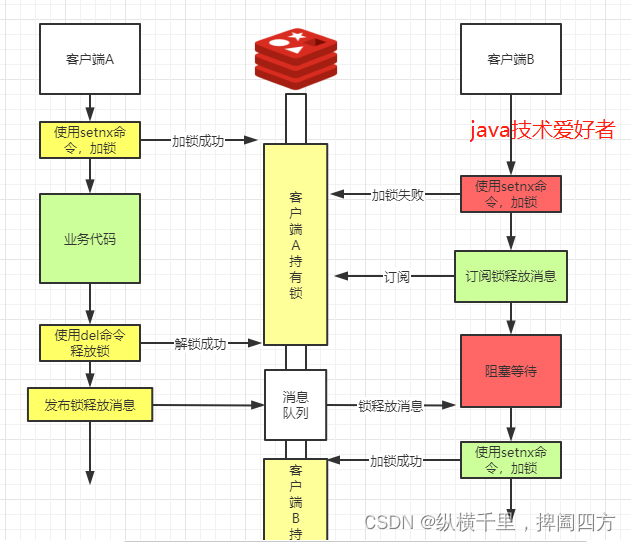
【征服redis15】分布式锁的功能与整体设计方案
目录 1. 分布式锁的概念 2.基于数据库做分布式锁 2.1 基于表主键唯一做分布式锁 2.2 基于表字段版本号做分布式锁 2.3 基于数据库排他锁做分布式锁 3.使用Redis做分布式锁 3.1 redis实现分布式锁的基本原理 3.2 问题一:增加超时机制,防止长期持有…...

MATLAB中实现机械臂逆运动学求解的方法之一是使用阻尼最小二乘法
MATLAB中实现机械臂逆运动学求解的方法之一是使用阻尼最小二乘法。阻尼最小二乘法通常用于处理数值求解问题中的不稳定性和噪声。以下是一个简单的MATLAB代码示例,演示了机械臂逆运动学的阻尼最小二乘法求解: % 机械臂参数 L1 1; % 机械臂长度 L2 1;…...
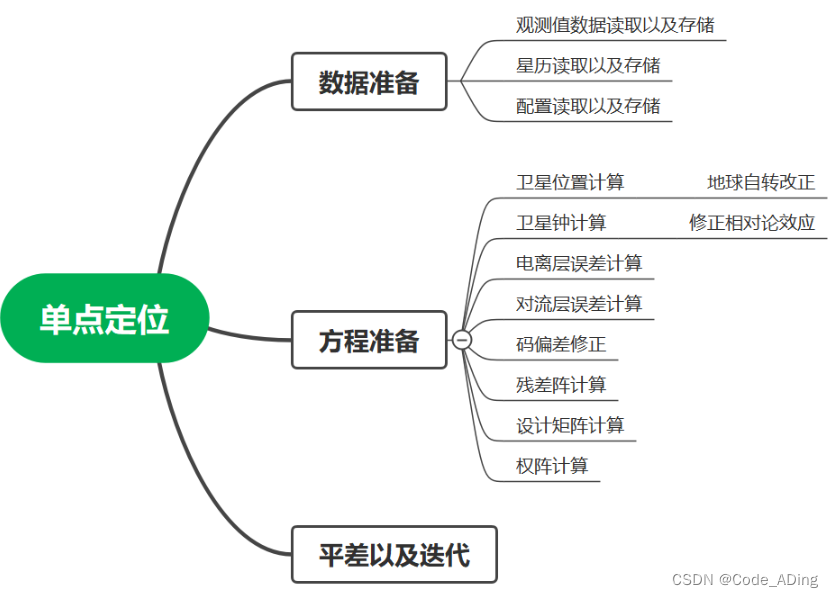
2024.1.24 GNSS 学习笔记
1.伪距观测值公式 2.载波相位观测值公式 3.单点定位技术(Single Point Positionin, SPP) 仅使用伪距观测值,不使用其他的辅助信息获得ECEF框架下绝对定位技术。 使用广播星历的轨钟进行定位,考虑到轨钟的米级精度,所以对于<1米的误差&…...
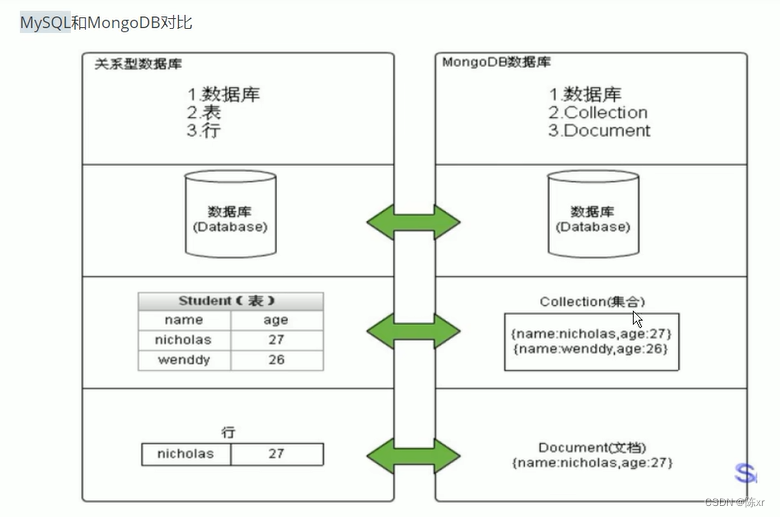
2024-01-22(MongoDB)
1.Mongodb使用的业务场景: 传统的关系型数据库/mysql在“三高”需求以及应对web2.0的网站需求面前,有点力不从心,什么是“三高”需求: a. 对数据库高并发的读写需求 b. 对海量数据的高效率存储和访问需求 c. 对数据库的高可扩…...

Android Wi-Fi 连接失败日志分析
1. Android wifi 关键日志总结 (1) Wi-Fi 断开 (CTRL-EVENT-DISCONNECTED reason3) 日志相关部分: 06-05 10:48:40.987 943 943 I wpa_supplicant: wlan0: CTRL-EVENT-DISCONNECTED bssid44:9b:c1:57:a8:90 reason3 locally_generated1解析: CTR…...

PHP和Node.js哪个更爽?
先说结论,rust完胜。 php:laravel,swoole,webman,最开始在苏宁的时候写了几年php,当时觉得php真的是世界上最好的语言,因为当初活在舒适圈里,不愿意跳出来,就好比当初活在…...

前端倒计时误差!
提示:记录工作中遇到的需求及解决办法 文章目录 前言一、误差从何而来?二、五大解决方案1. 动态校准法(基础版)2. Web Worker 计时3. 服务器时间同步4. Performance API 高精度计时5. 页面可见性API优化三、生产环境最佳实践四、终极解决方案架构前言 前几天听说公司某个项…...

376. Wiggle Subsequence
376. Wiggle Subsequence 代码 class Solution { public:int wiggleMaxLength(vector<int>& nums) {int n nums.size();int res 1;int prediff 0;int curdiff 0;for(int i 0;i < n-1;i){curdiff nums[i1] - nums[i];if( (prediff > 0 && curdif…...
指令的指南)
在Ubuntu中设置开机自动运行(sudo)指令的指南
在Ubuntu系统中,有时需要在系统启动时自动执行某些命令,特别是需要 sudo权限的指令。为了实现这一功能,可以使用多种方法,包括编写Systemd服务、配置 rc.local文件或使用 cron任务计划。本文将详细介绍这些方法,并提供…...

SpringTask-03.入门案例
一.入门案例 启动类: package com.sky;import lombok.extern.slf4j.Slf4j; import org.springframework.boot.SpringApplication; import org.springframework.boot.autoconfigure.SpringBootApplication; import org.springframework.cache.annotation.EnableCach…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

浪潮交换机配置track检测实现高速公路收费网络主备切换NQA
浪潮交换机track配置 项目背景高速网络拓扑网络情况分析通信线路收费网络路由 收费汇聚交换机相应配置收费汇聚track配置 项目背景 在实施省内一条高速公路时遇到的需求,本次涉及的主要是收费汇聚交换机的配置,浪潮网络设备在高速项目很少,通…...

安宝特案例丨Vuzix AR智能眼镜集成专业软件,助力卢森堡医院药房转型,赢得辉瑞创新奖
在Vuzix M400 AR智能眼镜的助力下,卢森堡罗伯特舒曼医院(the Robert Schuman Hospitals, HRS)凭借在无菌制剂生产流程中引入增强现实技术(AR)创新项目,荣获了2024年6月7日由卢森堡医院药剂师协会࿰…...

【JVM】Java虚拟机(二)——垃圾回收
目录 一、如何判断对象可以回收 (一)引用计数法 (二)可达性分析算法 二、垃圾回收算法 (一)标记清除 (二)标记整理 (三)复制 (四ÿ…...
