5-4 D. DS串应用—最长重复子串
题目描述
求串的最长重复子串长度(子串不重叠)。例如:abcaefabcabc的最长重复子串是串abca,长度为4。
输入
测试次数t
t个测试串
输入样例:
3
abcaefabcabc
szu0123szu
szuabcefg
输出
对每个测试串,输出最长重复子串长度,若没有重复子串,输出-1.
输出样例:
4
3
-1
思路
代码
#include <iostream>
using namespace std;int getNextMax(string s){s += " ";int len = s.length(), i=1, j=0;int next[len+1];next[1] = 0;while(i < len){if(j == 0 || s[i-1] == s[j-1]){i++;j++;next[i] = j;}else{j = next[j];}}int maxNum=1;for(int i = 1; i <= len; i++){if(next[i] > maxNum){maxNum = next[i];}}if(maxNum == 1){return -1;}else{return maxNum-1;}
}int main()
{int t;string s;cin >> t;while(t--){cin >> s;int res = getNextMax(s);cout << res << endl;}return 0;
}相关文章:

5-4 D. DS串应用—最长重复子串
题目描述 求串的最长重复子串长度(子串不重叠)。例如:abcaefabcabc的最长重复子串是串abca,长度为4。 输入 测试次数t t个测试串 输入样例: 3 abcaefabcabc szu0123szu szuabcefg 输出 对每个测试串,输出最…...

C语言实现12种排序算法
1.冒泡排序 思路:比较相邻的两个数字,如果前一个数字大,那么就交换两个数字,直到有序。 时间复杂度:O(n^2),稳定性:这是一种稳定的算法。 代码实现: void bubble_sort(int arr[],…...

C语言应用实例——贪吃蛇
(图片由AI生成) 0.贪吃蛇游戏背景 贪吃蛇游戏,最早可以追溯到1976年的“Blockade”游戏,是电子游戏历史上的一个经典。在这款游戏中,玩家操作一个不断增长的蛇,目标是吃掉出现在屏幕上的食物,…...

Mac如何设置一位数密码?
一、问题 Mac如何设置一位数密码? 二、解答 1、打开终端 2、清除全局账户策略 sudo pwpolicy -clearaccountpolicies 输入开机密码,这里是看不见的,输入完回车即可 3、重新设置密码 (1)打开设置-->用户和群组…...

运动编辑学习笔记
目录 跳舞重建: 深度运动重定向 Motion Preprocessing Tool anim_utils MotionBuilder 跳舞重建: https://github.com/Shimingyi/MotioNet 深度运动重定向 https://github.com/DeepMotionEditing/deep-motion-editin 游锋生/deep-motion-editin…...
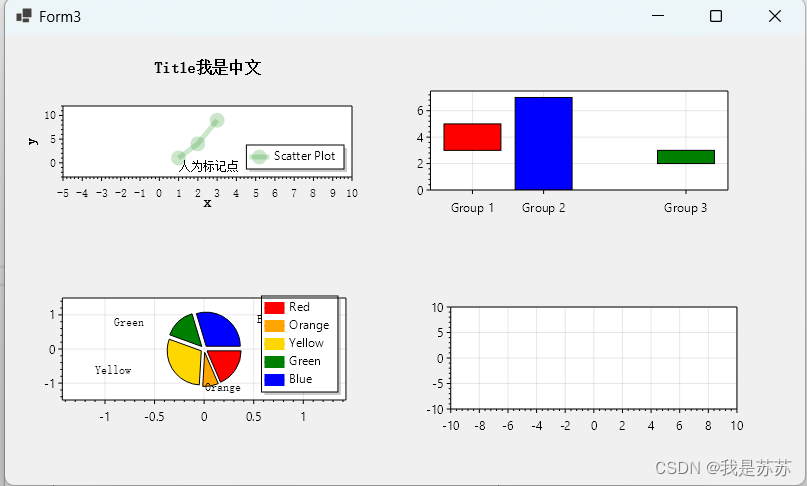
C#小结:ScottPlot 5.0在VS2022桌面开发的应用(以winform为例)
目录 一、官网文档地址 二、在VS2022中安装Scottplot 三、拖动Scottplot 四、使用Scottplot 五、效果图 一、官网文档地址 官网地址:ScottPlot 5.0 食谱 本文内容来自于官网,选取了官网的一些比较好用的功能展示,如需学习更多功能&a…...

Jmeter性能测试: Jmeter 5.6.3 分布式部署
目录 一、实验 1.环境 2.jmeter 配置 slave 代理压测机 3.jmeter配置master控制器压测机 4.启动slave从节点检查 5.启动master主节点检查 6.运行jmeter 7.观察jmeter-server主从节点变化 二、问题 1.jmeter 中间请求和响应乱码 一、实验 1.环境 (1&#…...

跟着cherno手搓游戏引擎【15】DrawCall的封装
目标: Application.cpp:把渲染循环里的glad代码封装成自己的类: #include"ytpch.h" #include "Application.h"#include"Log.h" #include "YOTO/Renderer/Renderer.h" #include"Input.h"namespace YO…...
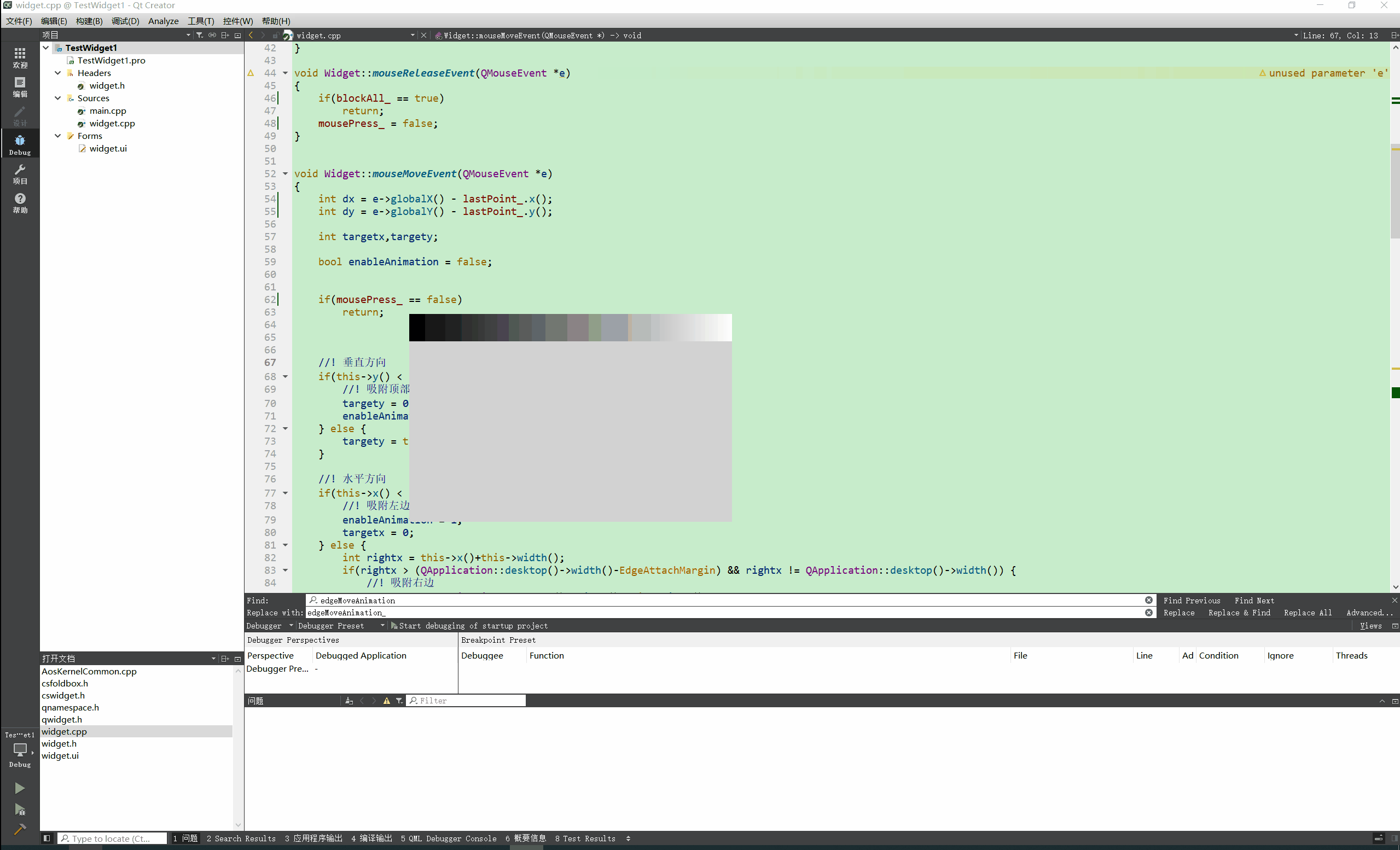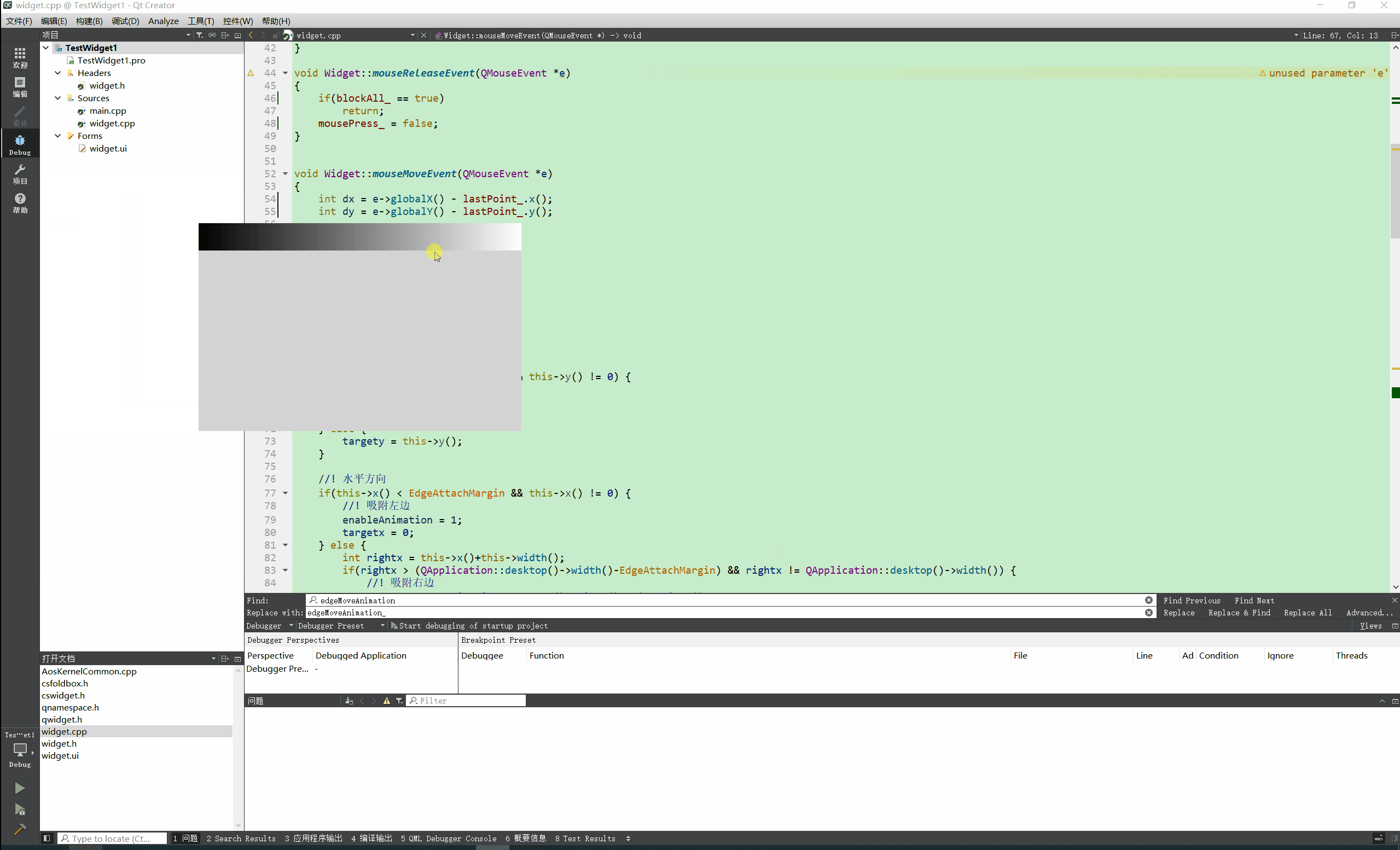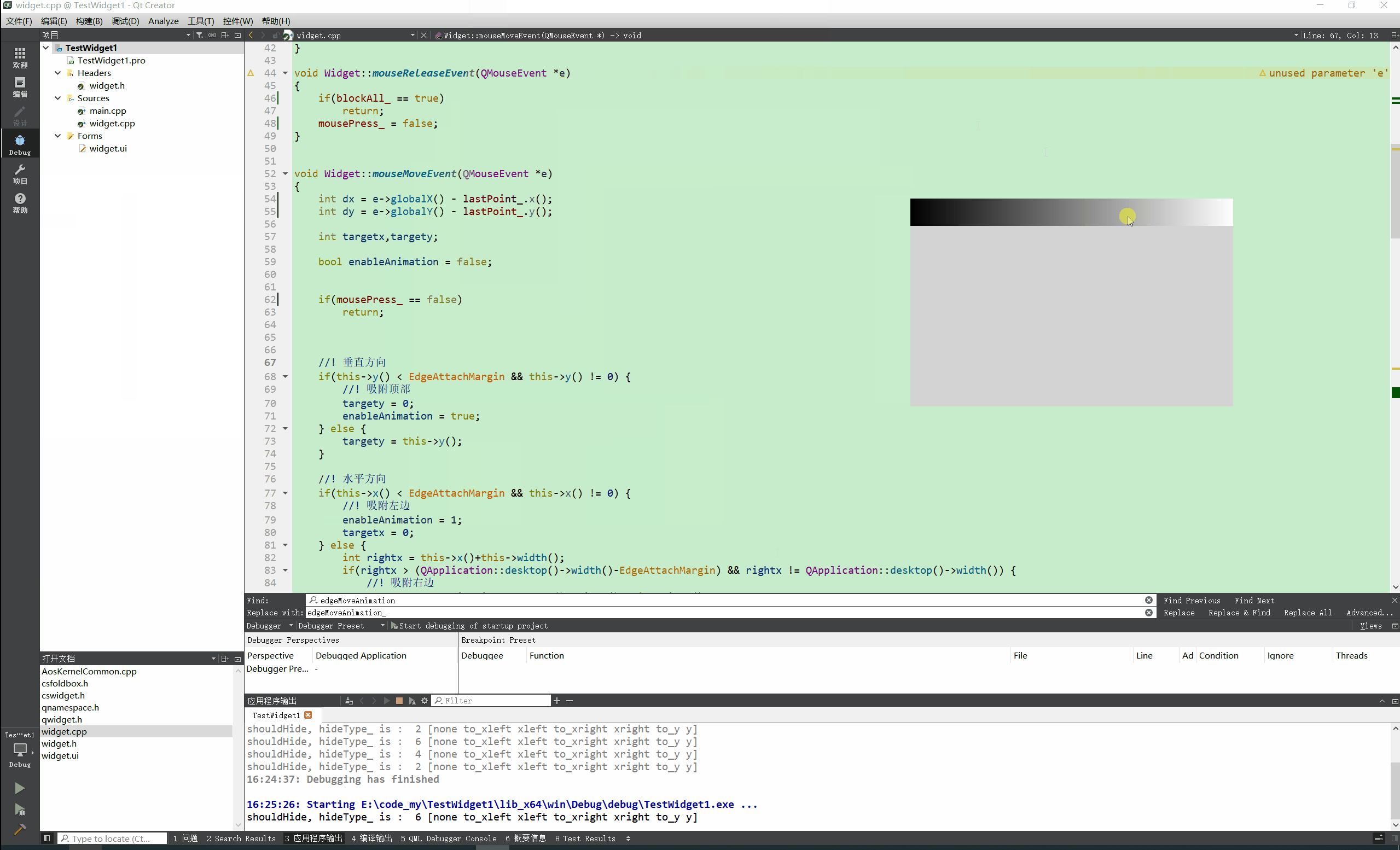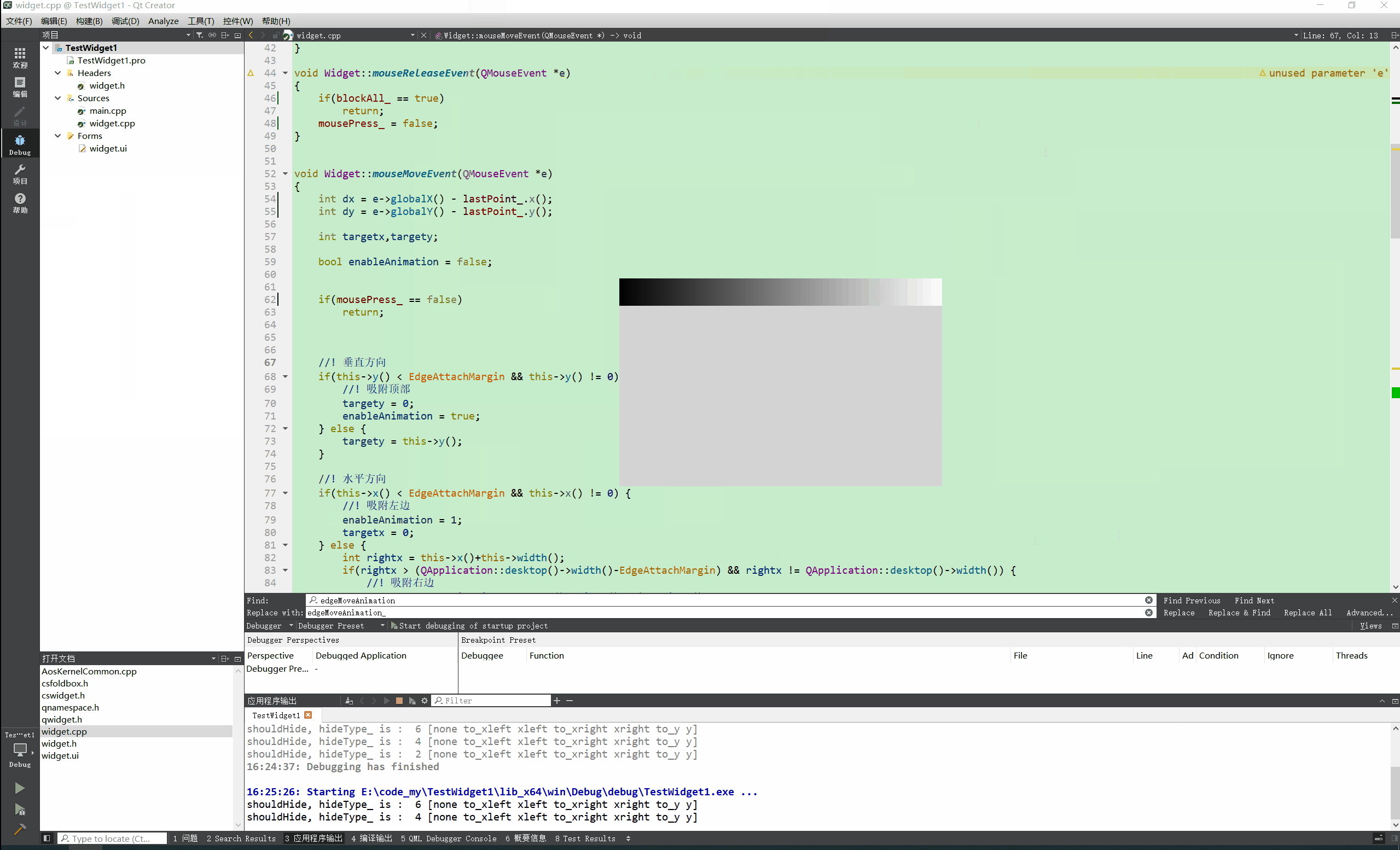
Qt实现窗口吸附屏幕边缘 自动收缩
先看效果: N年前的QQ就可以吸附到屏幕边缘,聊天时候非常方便,不用点击状态栏图标即可呼出QQ界面 自己尝试做了一个糙版的屏幕吸附效果。 关键代码: void Widget::mouseMoveEvent(QMouseEvent *e) {int dx e->globalX() - l…...
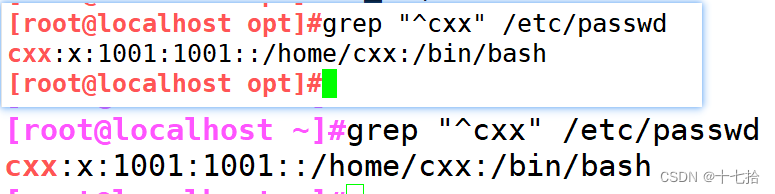
shell脚本之免交互
目录 一、Here Document 免交互 1、交互与免交互的概念 2、 Here Document 概述 二、Here Document 应用 1、使用cat命令多行重定向 2、使用tee命令多行重定向 3、使用read命令多行重定向 4、使用wc -l统计行数 5、使用passwd命令用户修改密码 6、Here Document 变量…...
Ajax入门与使用
目录 ◆ AJAX 概念和 axios 使用 什么是 AJAX? 怎么发送 AJAX 请求? 如何使用axios axios 函数的基本结构 axios 函数的使用场景 1 没有参数的情况 2 使用params参数传参的情况 3 使用data参数来处理请求体的数据 4 上传图片等二进制的情况…...
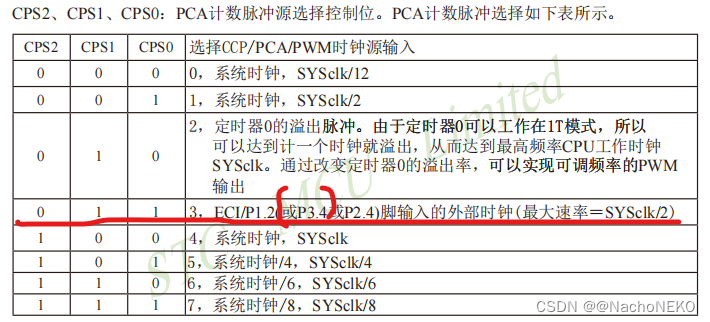
蓝桥杯备战——11.NE555测频
1.分析原理图 我们可以看到,上图就是一个NE555构建的方波发生电路,输出方波频率1.44/2(R8Rb3)C,如果有不懂NE555内部结构,工作原理的,可以到B站学习。实在不懂仿真也行,比如我下面就是仿真结果: 然后就是下…...

代码随想录算法训练营第三十三天|509. 斐波那契数 ,● 70. 爬楼梯 , 746. 使用最小花费爬楼梯
确定dp数组(dp table)以及下标的含义确定递推公式dp数组如何初始化确定遍历顺序举例推导dp数组 代码随想录 视频:从此再也不怕动态规划了,动态规划解题方法论大曝光 !| 理论基础 |力扣刷题总结| 动态规划入门_哔哩哔哩…...

Node.js 文件系统操作指南
文章目录 Node.js 文件系统操作完全指南一、引言二、基本文件操作2.1 读取文件2.2 写入文件2.3 追加内容到文件 三、文件与目录的创建与删除3.1 创建文件3.2 创建目录3.3 删除文件3.4 删除目录 四、文件与目录的信息查询4.1 检查文件或目录是否存在4.2 获取文件信息4.3 获取目录…...

Kotlin 协程1:深入理解withContext
Kotlin 协程1:深入理解withContext 引言 在现代编程中,异步编程已经变得非常重要。在 Kotlin 中,协程提供了一种优雅和高效的方式来处理异步编程和并发。在这篇文章中,我们将深入探讨 Kotlin 协程中的一个重要函数:wi…...
(自用)learnOpenGL学习总结-高级OpenGL-几何着色器
在顶点着色器和片段着色器中间还有一个几何着色器。 几何着色器的输入是一个图元的一组顶点,在几何着色器中进行任意变换之后再给片段着色器,可以变成完全不一样的图元、可以生成更多的顶点。 #version 330 core layout (points) in; layout (line_str…...
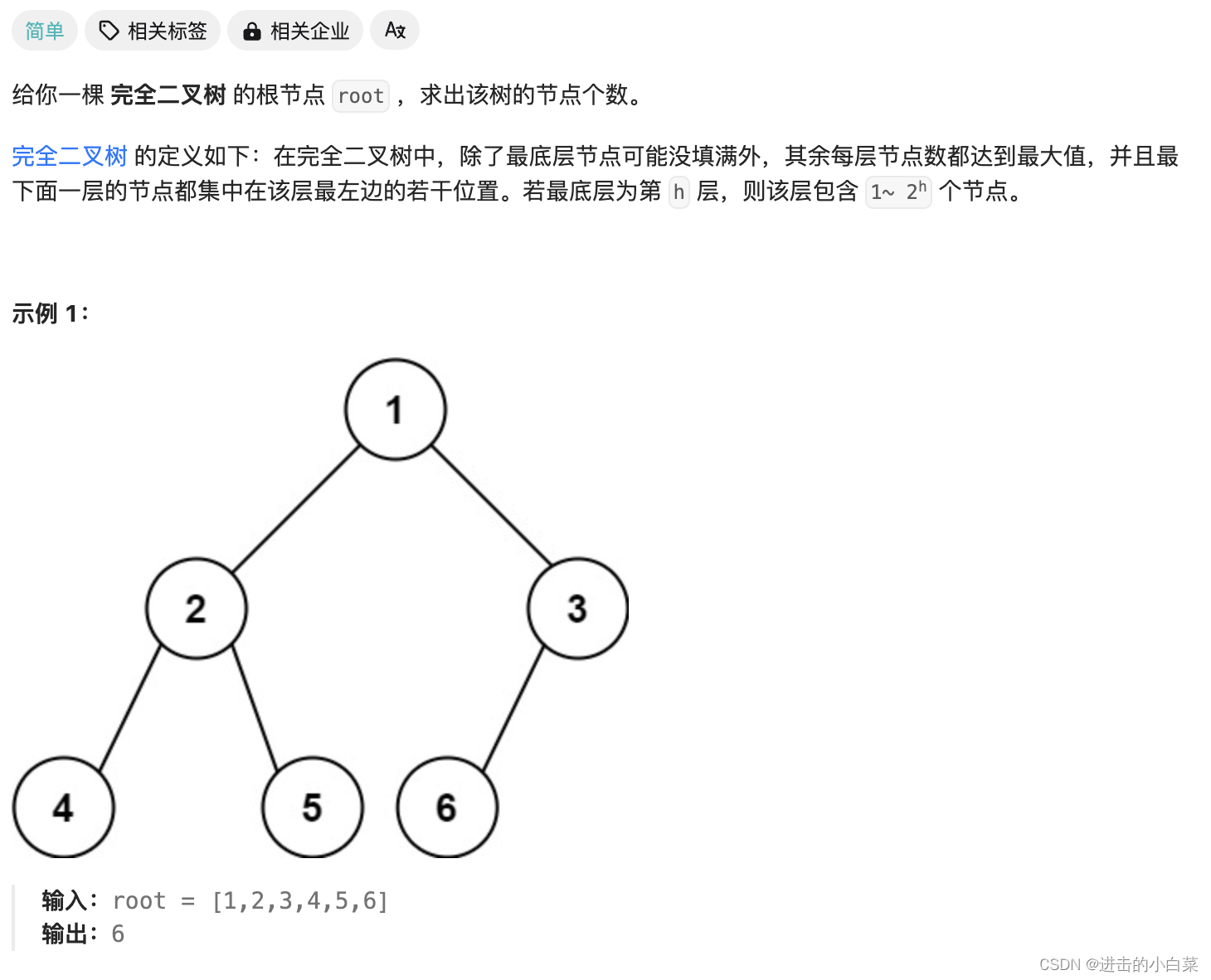
坚持刷题 | 完全二叉树的节点个数
Hello,大家好,我是阿月!坚持刷题,老年痴呆追不上我,今天刷:完全二叉树的节点个数 题目 222.完全二叉树的节点个数 代码实现 class TreeNode {int val;TreeNode left, right;public TreeNode(int val) …...

K8S网络
一、介绍 k8s不提供网络通信,提供了CNI接口(Container Network Interface,容器网络接口),由CNI插件实现完成。 1.1 Pod通信 1.1.1 同一节点Pod通信 Pod通过虚拟Ethernet接口对(Veth Pair)与外部通信,Veth…...

【蓝桥杯51单片机入门记录】LED
目录 一、基础 (1)新建工程 (2)编写前准备 二、LED (1)点亮LED灯 (2)LED闪烁 延时函数的生成(stc-isp中生成) 实现 (3)流水灯…...
)
轻松使用python将PDF转换为图片(成功)
使用PyMuPDF(fitz)将PDF转换为图片 在处理PDF文件时,我们经常需要将PDF页面转换为图片格式,以便于在网页、文档或应用程序中显示。Python提供了多种方式来实现这一需求,本文将介绍如何使用PyMuPDF(也称为f…...

C++:std::is_convertible
C++标志库中提供is_convertible,可以测试一种类型是否可以转换为另一只类型: template <class From, class To> struct is_convertible; 使用举例: #include <iostream> #include <string>using namespace std;struct A { }; struct B : A { };int main…...

【SQL学习笔记1】增删改查+多表连接全解析(内附SQL免费在线练习工具)
可以使用Sqliteviz这个网站免费编写sql语句,它能够让用户直接在浏览器内练习SQL的语法,不需要安装任何软件。 链接如下: sqliteviz 注意: 在转写SQL语法时,关键字之间有一个特定的顺序,这个顺序会影响到…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

什么是EULA和DPA
文章目录 EULA(End User License Agreement)DPA(Data Protection Agreement)一、定义与背景二、核心内容三、法律效力与责任四、实际应用与意义 EULA(End User License Agreement) 定义: EULA即…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决
Spring Cloud Gateway 中自定义验证码接口返回 404 的排查与解决 问题背景 在一个基于 Spring Cloud Gateway WebFlux 构建的微服务项目中,新增了一个本地验证码接口 /code,使用函数式路由(RouterFunction)和 Hutool 的 Circle…...

处理vxe-table 表尾数据是单独一个接口,表格tableData数据更新后,需要点击两下,表尾才是正确的
修改bug思路: 分别把 tabledata 和 表尾相关数据 console.log() 发现 更新数据先后顺序不对 settimeout延迟查询表格接口 ——测试可行 升级↑:async await 等接口返回后再开始下一个接口查询 ________________________________________________________…...

HubSpot推出与ChatGPT的深度集成引发兴奋与担忧
上周三,HubSpot宣布已构建与ChatGPT的深度集成,这一消息在HubSpot用户和营销技术观察者中引发了极大的兴奋,但同时也存在一些关于数据安全的担忧。 许多网络声音声称,这对SaaS应用程序和人工智能而言是一场范式转变。 但向任何技…...

区块链技术概述
区块链技术是一种去中心化、分布式账本技术,通过密码学、共识机制和智能合约等核心组件,实现数据不可篡改、透明可追溯的系统。 一、核心技术 1. 去中心化 特点:数据存储在网络中的多个节点(计算机),而非…...

解析“道作为序位生成器”的核心原理
解析“道作为序位生成器”的核心原理 以下完整展开道函数的零点调控机制,重点解析"道作为序位生成器"的核心原理与实现框架: 一、道函数的零点调控机制 1. 道作为序位生成器 道在认知坐标系$(x_{\text{物}}, y_{\text{意}}, z_{\text{文}}…...
