【冲刺蓝桥杯的最后30天】day2
大家好😃,我是想要慢慢变得优秀的向阳🌞同学👨💻,断更了整整一年,又开始恢复CSDN更新,从今天开始更新备战蓝桥30天系列,一共30天,如果对你有帮助或者正在备战蓝桥杯的小伙伴可以支持一下哦!~不能说肯定是干货,但会让你有所收获!💓💓💓
🍭🍭我们总是在生活扮演各种角色,却唯独很少扮演自己🍭🍭
奇数倍数 - 蓝桥云课 (lanqiao.cn)
思路:纯暴力模拟就行,填空题只要答案没什么好说的
public static void main(String[] args) {for (int i = 2; ; i++) {if (check(i * 2019)) {System.out.println(i * 2019);break;}}}public static boolean check(int n) {while (n != 0) {int tmp = n % 10;if (tmp % 2 == 0) return false;n /= 10;}return true;}求值 - 蓝桥云课 (lanqiao.cn)
思路①:纯暴力模拟,因为数比较小,加上是一道填空题,考场遇到用的方法越简单越好
思路②:约数个数定理+唯一整数分解定理,一道数论题,相当于,已知约数个数,求对应的最小的自然数
思路①
//这段代码在idea跑着也挺费劲的,3秒左右出答案,但放在oj平台上肯定超时,我们只用System.out.println(45360);提交就行了
public static void main(String[] args) {for (int i = 1; ; i++) {int count = 0;for (int j = 1; j <= i; j++) {if(i % j == 0) count++;if (count == 100) {System.out.println(i);//45360return;}}}}思路②

这道题本质其实是约数个数定理的逆用
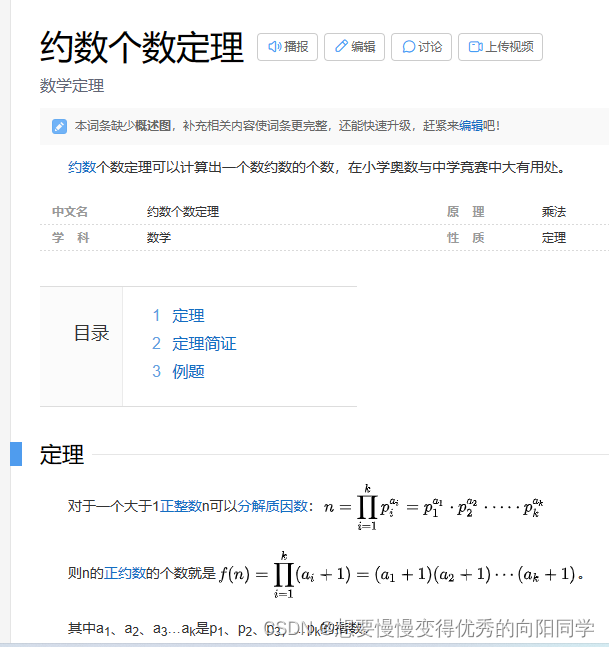
这个是百度定义的还有例题
例题:正整数378000共有多少个正约数?
解:将378000分解质因数378000=2^4×3^3×5^3×7^1//根据唯一整数分解定理我们知道任何一个整数都能拆成一堆质数的幂相乘,这里的质是2357
由约数个数定理可知378000共有正约数(4+1)×(3+1)×(3+1)×(1+1)=160个。//又根据约数个数定理,一个数的所有质因数数的幂+1之和相乘是这个数所有约数的之和已知约数个数是100,100是根据约数个数定理,是正整数t(t是题目让我们求的值)的所有素因子的幂+1的和相乘得到的,那我们逆向思考可以得到,把10根据整数唯一分级定理拆成100=2*2*5*5,又因为求最小,把最小质数按顺序找到四个,分别是2345,把最大的幂给最小的质数(记得-1),答案就是2^(5-1)*3^(5-1)*5^(2-1)*7^(2-1),得到最小的自然数
求和 - 蓝桥云课 (lanqiao.cn)
思路:前缀和,看S的表达式,会发现如果提取一个公因数那么S=a1*(a2+a3..an)+a2*(a3+..an)...这样思路一下子就清晰起来了,括号里面的数据就是在暗示我们用前缀和
//因为这道题输入数据达到200000,蓝桥比赛是IO赛制的比赛,提交根本不知道对不对,可能有数据太大超时了,为了稳妥
//避免这种情况可能的发生,我们这里使用了快读,虽然说正常的输入输出也能过,但如果真正的比赛你是不清楚的,稳一点总是好的
public static void main(String[] args) throws IOException {long ans = 0;BufferedReader br = new BufferedReader(new InputStreamReader(System.in));String[] s = br.readLine().split(" ");int n = Integer.parseInt(s[0]);s = br.readLine().split(" ");for (int i = 1; i <= n; i++) {a[i] = Integer.parseInt(s[i - 1]);}for (int i = 1; i <= n; i++) {a[i] += a[i - 1];}for (int i = 1; i <= n; i++) {//这里写的有点复杂其实就是a[1]*(a[2]+a[3]..a[n])因为是前缀和数组,a[1]表达起来有点费劲//当然这道题甚至可以不用专门再写个前缀和循环了,因为是从头到尾遍历了,直接用一个sum变量来接受更加简单//long sum = 0;//for (int i = 0; i < n; i++) {//ans+=a[i]*sum;//sum+=a[i];//}ans += (long) (a[i] - a[i - 1]) * (a[n] - a[i]);}System.out.println(ans);}相关文章:

【冲刺蓝桥杯的最后30天】day2
大家好😃,我是想要慢慢变得优秀的向阳🌞同学👨💻,断更了整整一年,又开始恢复CSDN更新,从今天开始更新备战蓝桥30天系列,一共30天,如果对你有帮助或者正在备…...

docker系列1:docker安装
传送门 docker官网地址: Docker: Accelerated, Containerized Application Development 安装地址:Install Docker Engine docker hub地址 docker hub:Docker 安装步骤 前置条件 由于安装docker,需要根据操作系统版本选择…...
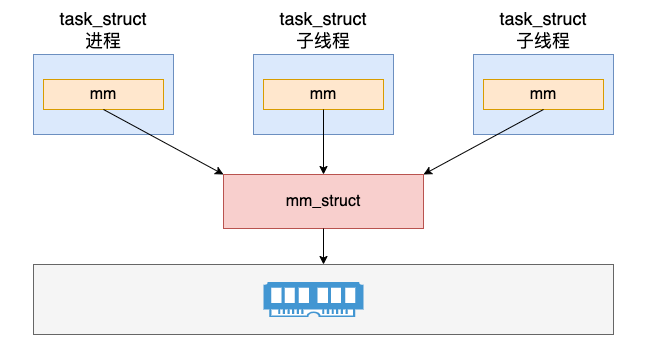
内核角度谈谈Linux进程和线程
目录前言内核对进程和线程的表示创建进程的过程创建线程的过程创建进程和线程的异同揭秘 do_fork 系统调用结论前言 昨天面试的时候,面试官问我了个平平淡淡的问题–>“聊聊Linux中进程和线程”; 相比大家不管是在考试还是面试中或多或少都遇到过这个问题&…...

【mmdeploy部署系列】使用Tensorrt加速部署mmpose人体姿态库
【mmdeploy部署系列】使用Tensorrt加速部署mmpose人体姿态库0.引言1.安装mmcv2.使用mmpose(1)安装mmpose(2)运行mmpose3.使用mmdeploy(1)安装ppl.cv(2)编译安装mmdeploy(…...

IDEA 每次新建工程都要重新配置 Maven 解决方案
IDEA 每次新建工程都要重新配置 Maven 解决方案 IDEA 每次新建工程都要重新配置 Maven,是一件相当浪费时间的事情。这是因为在创建一个项目后,在 File -> Settings -> Build,Execution,Deployment -> Build Tools -> Maven下配置了 Maven h…...
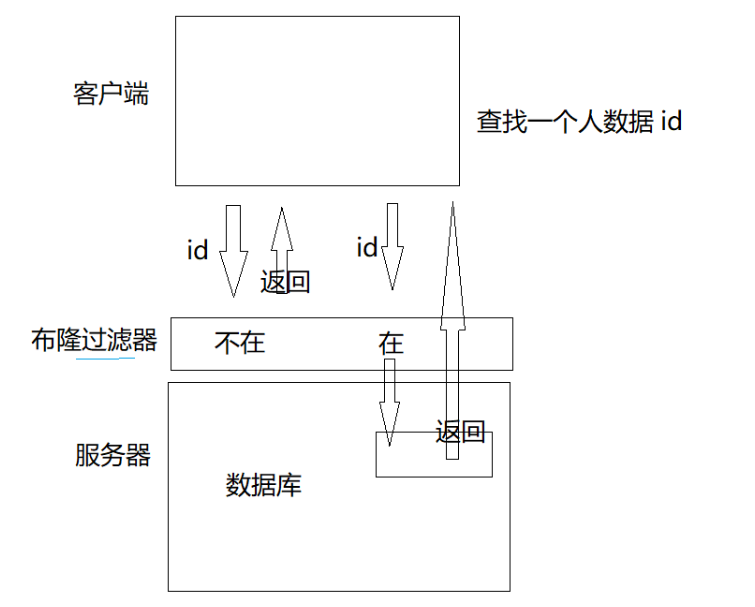
【C++修炼之路】25.哈希应用--布隆过滤器
每一个不曾起舞的日子都是对生命的辜负 布隆过滤器前言一.布隆过滤器提出二.布隆过滤器概念三. 布隆过滤器的操作3.1 布隆过滤器的插入3.2 布隆过滤器的查找3.3 布隆过滤器的删除四.布隆过滤器的代码4.1 HashFunc的仿函数参考4.2 BloomFilter.h五.布隆过滤器的优缺点六.布隆过滤…...

linux入门---权限
目录标题什么是权限人的分类为什么会有所属组查看文件属性文件的分类如何查看权限文件不同权限的表现rwx权限修改八进制权限修改umask有关内容文件中人的修改目录不同权限的表现rwx什么是权限 首先来看一个例子:比如说我没有爱奇艺的vip,那么我也就没有…...
Unity记录2.1-动作-多段跳、蹬墙跳、墙体滑落
文章首发及后续更新:https://mwhls.top/4450.html,无图/无目录/格式错误/更多相关请至首发页查看。 新的更新内容请到mwhls.top查看。 欢迎提出任何疑问及批评,非常感谢! 汇总:Unity 记录 摘要:实现跳跃、蹬…...
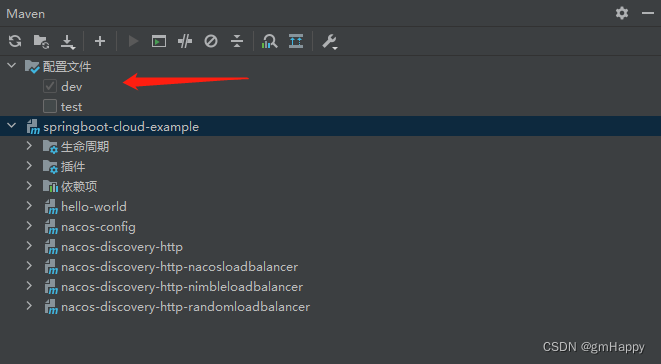
Spring Boot结合IDEA自带Maven插件快速切换profile | Spring Cloud 10
一、前言 IDEA是目前 Java 开发者中使用最多的开发工具,它有着简约的设计风格,强大的集成工具,便利的快捷键。 在项目项目整个开发运维周期中,我们的的项目往往需要根据不同的环境,使用不同的文件配置。 比如以下部…...
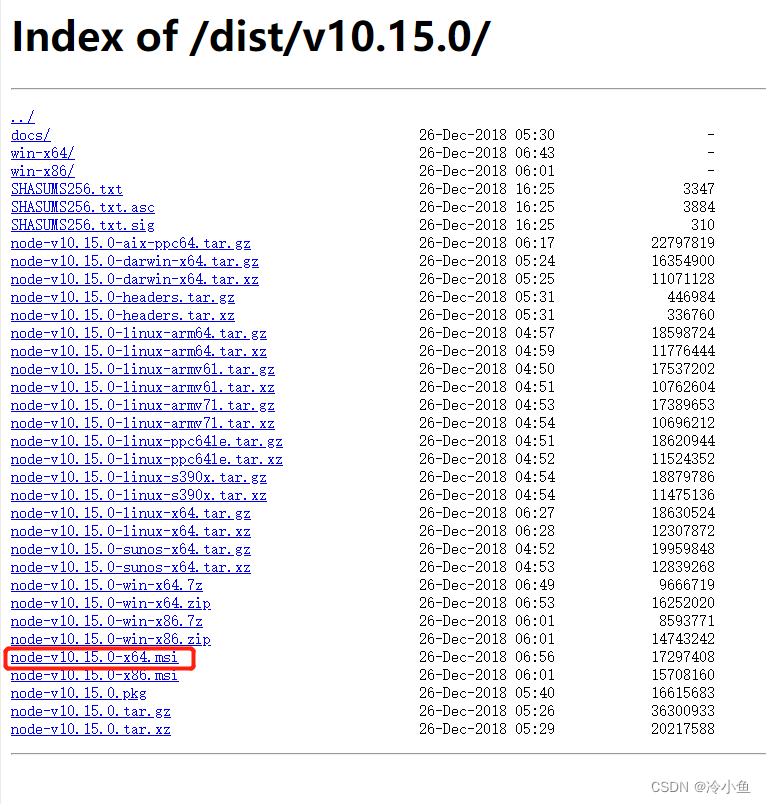
ES 7.7.0 数据迁移
本文使用 elasticdump 做数据迁移,支持在线和离线俩种方式,适用于数据量比较小的情况。 1、Node 安装 由于elasticdump 依赖于 node,首先需要安装下node。 1.1、 Linux 安装 $ wget https://nodejs.org/dist/v10.15.0/node-v10.15.0-linu…...

【玩转c++】vector讲解和模拟底层实现
本期主题:vector的讲解和模拟实现博客主页:小峰同学分享小编的在Linux中学习到的知识和遇到的问题小编的能力有限,出现错误希望大家不吝赐vector的介绍及使用1.1vector的介绍vector其实就是一个数组的模板 ,存放的数据可以改变而已…...

基本类型、包装类型、引用类型、String等作为实参传递后值会不会改变?
看了半天帖子,讲得乱七八糟,坑死了 [1] 先说结论 基本类型、包装类型、String类型作为参数传递之后,在方法里面修改他们的值,原值不会改变!引用类型不一定,要看是怎么修改它的。 [2] 为什么基本类型、包装类…...
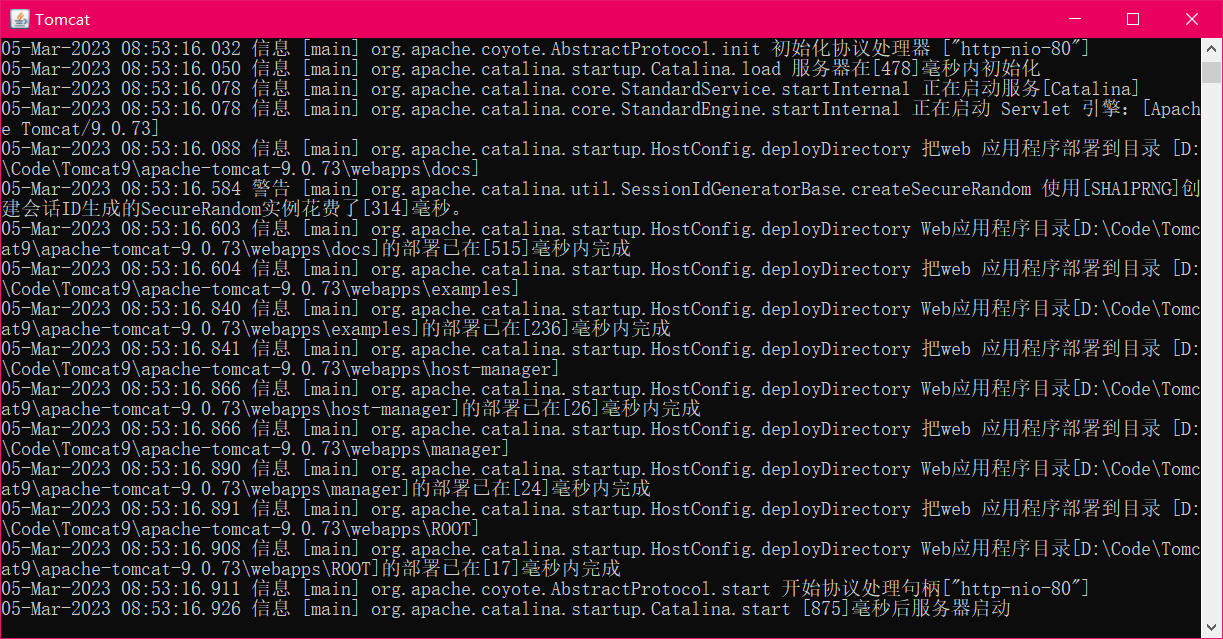
Tomcat服务器配置以及问题解决方案
文章目录01 Tomcat简介02 Tomcat的安装03 Tomcat的使用启动Tomcat服务器 (解决一闪而过)测试 Tomcat 是否启动Tomcat 服务器的关闭04 Tomcat的配置配置端口控制台配置(乱码解决)部署工程到Tomcat中01 Tomcat简介 Tomcat是一款开源…...

【Node.js】HTTP协议、HTTP的请求报文和响应报文
HTTP协议、HTTP的请求报文和响应报文HTTP协议HTTP主要特点HTTP的请求报文和响应报文请求报文请求行请求消息头空行请求体响应报文响应状态行响应消息头空行响应体总结HTTP协议 HTTP 全称为超文本传输协议,是用于从WWW服务器传输超文本到本地浏览器的传送协议&#…...

CodeForce 455A. Boredom
题目链接 CodeForce 455A. Boredom 思路 因为跟序列的下标无关,所以先对数组a排个序。那么每次选择只会影响两侧的元素。 记号 令dp[i]dp[i]dp[i]表示排序后a[1..i]a[1..i]a[1..i]能够获得的最大点数。 但是这样不足以区分是否当前元素可以被使用,所…...

geoserver之BlobStores使用
概述 geoserver是常用的地图服务器之一,除了基本的能力之外,也提供了很多的插件方便大家使用。在本文,讲述一下如何在geoserver中使用BlobStores和gwc-sqlite-plugin插件实现地图的切片和部署。 BlobStores简介 在geoserver中,…...

跨域问题以及Ajax和Axios的区别
文章目录1. 同源策略2. 同源策略案例3. 什么是跨域4. 跨域解决方法4.1 Ajax的jsonp4.2 CORS方式4.3 Nginx 反向代理5. Axios 和 Ajax 的区别6. Axios 和 Ajax 的区别及优缺点6.1 Ajax:6.1.1 什么是Ajax6.1.2 Ajax的原理6.1.3 核心对象6.1.4 Ajax优缺点6.1.4.1 优点&…...
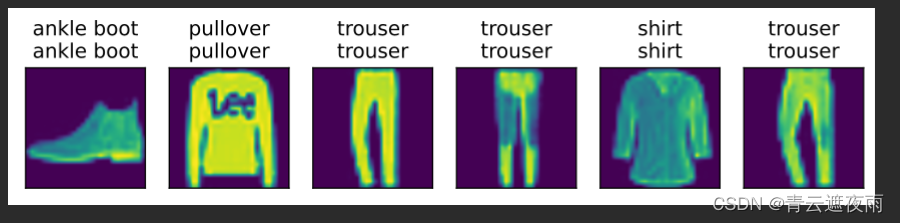
现代卷积神经网络(AlexNet)
专栏:神经网络复现目录 本章介绍的是现代神经网络的结构和复现,包括深度卷积神经网络(AlexNet),VGG,NiN,GoogleNet,残差网络(ResNet),稠密连接网络…...
单向非循环链表
1、顺序表遗留问题 1. 中间/头部的插入删除,时间复杂度为O(N) 2. 增容需要申请新空间,使用malloc、realloc等函数拷贝数据,释放旧空间。会有不小的消耗。 3. 当我们以2倍速度增容时,势必会有一定的空间浪费。例如当前容量为100&a…...

Vue2的基本内容(一)
目录 一、插值语法 二、数据绑定 1.单向数据绑定 2.双向数据绑定 三、事件处理 1.绑定监听 2.事件修饰符 四、计算属性computed和监视属性watch 1.计算属性-computed 2.监视属性-watch (1)通过 watch 监听 msg 数据的变化 (2&a…...

基于大模型的 UI 自动化系统
基于大模型的 UI 自动化系统 下面是一个完整的 Python 系统,利用大模型实现智能 UI 自动化,结合计算机视觉和自然语言处理技术,实现"看屏操作"的能力。 系统架构设计 #mermaid-svg-2gn2GRvh5WCP2ktF {font-family:"trebuchet ms",verdana,arial,sans-…...

【人工智能】神经网络的优化器optimizer(二):Adagrad自适应学习率优化器
一.自适应梯度算法Adagrad概述 Adagrad(Adaptive Gradient Algorithm)是一种自适应学习率的优化算法,由Duchi等人在2011年提出。其核心思想是针对不同参数自动调整学习率,适合处理稀疏数据和不同参数梯度差异较大的场景。Adagrad通…...

循环冗余码校验CRC码 算法步骤+详细实例计算
通信过程:(白话解释) 我们将原始待发送的消息称为 M M M,依据发送接收消息双方约定的生成多项式 G ( x ) G(x) G(x)(意思就是 G ( x ) G(x) G(x) 是已知的)࿰…...

如何在看板中体现优先级变化
在看板中有效体现优先级变化的关键措施包括:采用颜色或标签标识优先级、设置任务排序规则、使用独立的优先级列或泳道、结合自动化规则同步优先级变化、建立定期的优先级审查流程。其中,设置任务排序规则尤其重要,因为它让看板视觉上直观地体…...

java调用dll出现unsatisfiedLinkError以及JNA和JNI的区别
UnsatisfiedLinkError 在对接硬件设备中,我们会遇到使用 java 调用 dll文件 的情况,此时大概率出现UnsatisfiedLinkError链接错误,原因可能有如下几种 类名错误包名错误方法名参数错误使用 JNI 协议调用,结果 dll 未实现 JNI 协…...
:观察者模式)
JS设计模式(4):观察者模式
JS设计模式(4):观察者模式 一、引入 在开发中,我们经常会遇到这样的场景:一个对象的状态变化需要自动通知其他对象,比如: 电商平台中,商品库存变化时需要通知所有订阅该商品的用户;新闻网站中࿰…...

scikit-learn机器学习
# 同时添加如下代码, 这样每次环境(kernel)启动的时候只要运行下方代码即可: # Also add the following code, # so that every time the environment (kernel) starts, # just run the following code: import sys sys.path.append(/home/aistudio/external-libraries)机…...

Oracle11g安装包
Oracle 11g安装包 适用于windows系统,64位 下载路径 oracle 11g 安装包...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

VisualXML全新升级 | 新增数据库编辑功能
VisualXML是一个功能强大的网络总线设计工具,专注于简化汽车电子系统中复杂的网络数据设计操作。它支持多种主流总线网络格式的数据编辑(如DBC、LDF、ARXML、HEX等),并能够基于Excel表格的方式生成和转换多种数据库文件。由此&…...
