2-1 动手学深度学习v2-Softmax回归-笔记
回归 VS 分类
- 回归估计一个连续值
- 分类预测一个离散类别
从回归到多类分类
回归
- 单连续数值输出
- 输出的区间:自然区间 R \mathbb{R} R
- 损失:跟真实值的区别
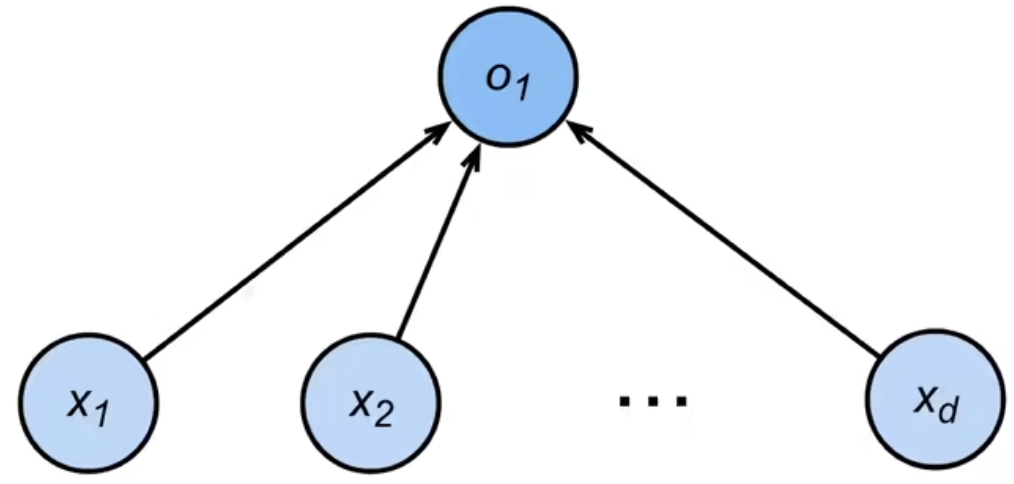
分类
- 通常多个输出(这个输出的个数是等于类别的个数)
- 输出的第 i i i个元素是用来预测第 i i i类的置信度
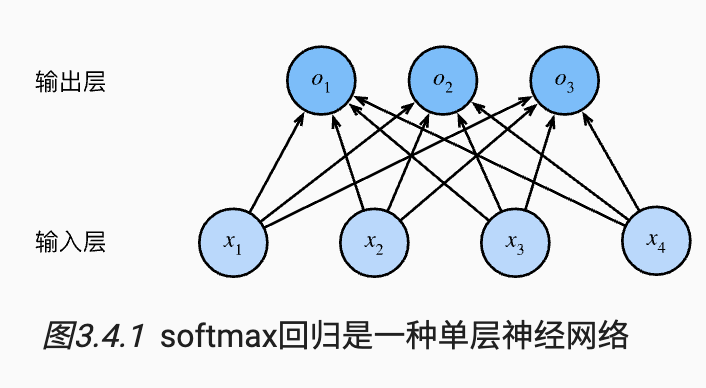
从回归到多类分类——均方损失
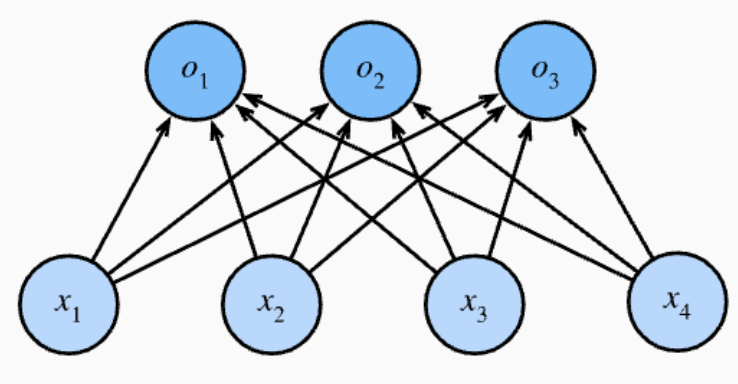
- 对类别进行一位有效编码(因为类别不是一个数,可能是一个字符串等等)
假设我们有 n n n个类别,我们可以用最简单的一位有效编码来进行编码。假设我们有 n n n个类别,那么我们的标号就是一个长为 n n n的向量,从 y 1 y_{1} y1到 y n y_{n} yn,其中,假设我的真实的类别是第 i i i个,那么 y i y_{i} yi等于 1 1 1,其他的元素全部等于 0 0 0。意思就是这个向量中,我们恰好有一个位置为 1 1 1,这个位置的下标表示第 i i i个元素,其他的元素全部为 0 0 0。
y = [ y 1 , y 2 , . . . , y n ] T \pmb{y}=[y_{1},y_{2},...,y_{n}]^{T} y=[y1,y2,...,yn]T
y i = { 1 i f i = y 0 o t h e r w i s e y_{i}= \begin{cases} 1 \quad if \quad i= y\\ 0 \quad otherwise \end{cases} yi={1ifi=y0otherwise - 使用均方损失训练(当我们有了编码以后,我们可以用最简单的回归问题的均方损失来训练,我们可以在不改动的情况下)
- 最大值最为预测(假设我们有我们训练出来的一个模型,我们做预测的时候,那么就是我们选取 i i i时的最大化 o i o_{i} oi即置信度的值,作为我的预测, i i i是我们预测的一个标号)
y ^ = a r g m a x i o i \hat{y}=\underset {i}{argmax} \ o_{i} y^=iargmax oi
从回归到多类分类——无校验比例
对于分类来讲,我们其实不关心,它们之间的实际的值,我们关心的是说,我是不是能够对正确类别的置信度特别大。
我们可以将我们的目标函数改为,我们需要使得我们对正确类 y y y的置信度,就是 o y o_{y} oy,要远远大于其他非正确类的 o i o_{i} oi,要大于某一个阈值, Δ \Delta Δ。
这样子能保证我的模型真正地能够将我的真正的类和不一样的类拉开距离。
虽然我们这里没有说你具体 o i o_{i} oi要什么样的值,大一点小一点都没关系,我们关心的是一个相对值,但是我们如果把值放在一个合适的区间,也会让我们后面的变得更加简单。
-
对类别进行一位有效编码
-
最大值最为预测 y ^ = a r g m a x i o i \hat{y}=\underset {i}{argmax} \ o_{i} y^=iargmax oi
-
需要更置信的识别正确类(大余量)
o y − o i ≥ Δ ( y , i ) o_{y}-o_{i}\geq\Delta(y,i) oy−oi≥Δ(y,i)
从回归到多类分类——校验比例
我们希望使得我们的输出能够是一个概率,现在我们的输出是 o 1 o_{1} o1一直到 o n o_{n} on,就是一个 o \pmb{o} o的一个向量。那么我们怎么做这个事情呢?
我们可以引入一个新的操作子,叫做 s o f t m a x softmax softmax,我们将 s o f t m a x softmax softmax作用在 o o o上面,得到一个 y ^ \pmb{\hat{y}} y^,它是一个长为 n n n的向量,但是它有我们要的属性,即它的每个元素都非负,而且它的和为1。
- 输出匹配概率(非负,和为 1 1 1)
y ^ = s o f t m a x ( o ) \pmb{\hat{y}}=softmax(\pmb{o}) y^=softmax(o) y ^ i = e x p ( o i ) ∑ k e x p ( o k ) \hat{y}_{i}=\frac{exp(o_{i})}{\sum_{k}exp(o_{k})} y^i=∑kexp(ok)exp(oi)具体我们的操作是说, y ^ \pmb{\hat{y}} y^里面的第 i i i个元素,它是等于 o \pmb{o} o里面的第 i i i个元素,作指数,指数的好处是说我不管它里面的值是多少,我都能够把它变成非负;再除以所有的 o k o_{k} ok作指数的和,这样我们能够保证 y ^ \pmb{\hat{y}} y^所有的元素加起来的和为 1 1 1。这样的好处就是说,我们的 y ^ \pmb{\hat{y}} y^它其实就是一个概率啦。
回忆一下,我们对真实标号的 y \pmb{y} y,也是作成一个概率,因为他刚好只有一个元素为 1 1 1,剩下的全部为 0 0 0,任何满足所有元素非负,且和为 1 1 1的,都可以当作一个概率。
那么我们就得到两个概率,一个是真实的 y \pmb{y} y的概率,一个是预测的 y ^ \pmb{\hat{y}} y^的概率。
- 概率 y \pmb{y} y和 y ^ \pmb{\hat{y}} y^的区别作为损失
Softmax和交叉熵损失
我们假设有两个离散概率 p \pmb{p} p和 q \pmb{q} q,都有 n n n个元素
- 交叉熵常用来衡量两个概率的区别 H ( p , q ) = ∑ i − p i l o g ( q i ) H(\pmb{p},\pmb{q})=\underset {i}{\sum}-p_{i}log(q_{i}) H(p,q)=i∑−pilog(qi)
- 将它作为损失
l ( y , y ^ ) = − ∑ i y i l o g y ^ i = − l o g y ^ y l(\pmb{y},\hat{\pmb{y}})=-\underset {i}{\sum}y_{i}log\hat{y}_{i}=-log\hat{y}_{y} l(y,y^)=−i∑yilogy^i=−logy^y我们知道,真实值里面只有 1 1 1个为 1 1 1,其余都为 0 0 0,因而公式可以简写为,负的 l o g log log对真实类别 y y y它的预测的 y ^ \hat{y} y^,就是对真实类别我的预测值求 l o g log log然后求负数。
可以看到,对分类问题来讲,我们不关心对非正确类的预测值,我们只关心对正确类的预测值它要执行度要多大。 - 其梯度是真实概率和预测概率的区别
∂ o i l ( y , y ^ ) = s o f t m a x ( o ) i − y i \partial_{o_{i}}l(\pmb{y},\pmb{\hat{y}})=softmax(\pmb{o})_{i}-y_{i} ∂oil(y,y^)=softmax(o)i−yi
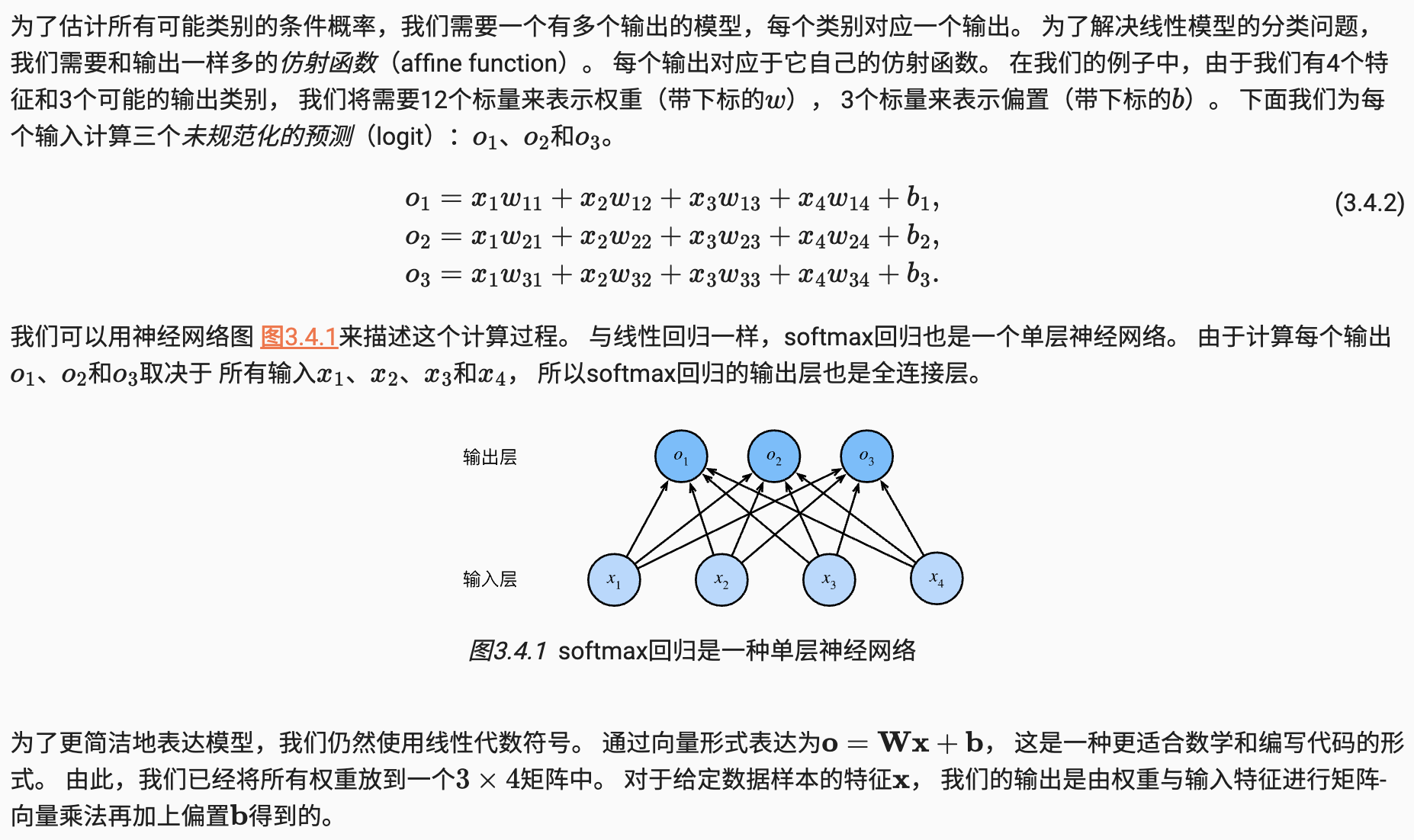

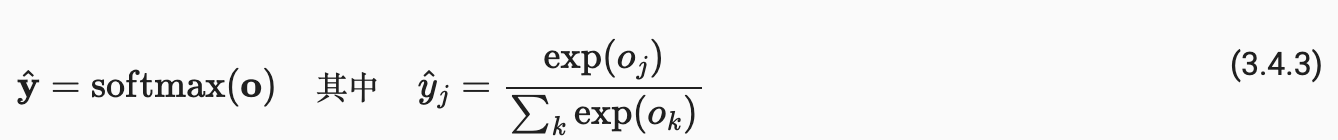
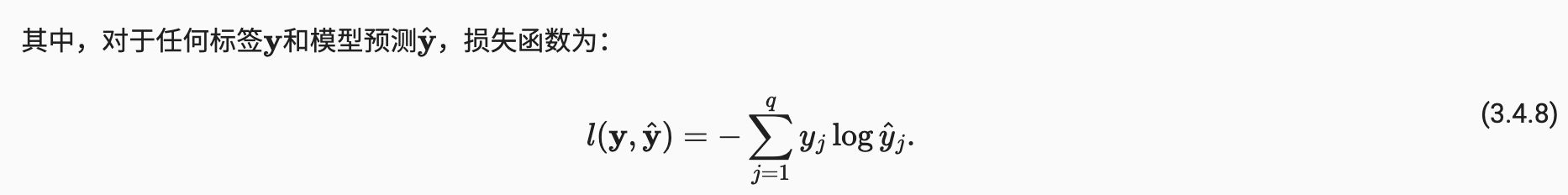

总结
- Softmax回归是一个多类分类模型
- 使用Softmax操作子得到每个类的预测置信度
- 使用交叉熵来衡量预测和标号的区别
相关文章:

2-1 动手学深度学习v2-Softmax回归-笔记
回归 VS 分类 回归估计一个连续值分类预测一个离散类别 从回归到多类分类 回归 单连续数值输出输出的区间:自然区间 R \mathbb{R} R损失:跟真实值的区别 分类 通常多个输出(这个输出的个数是等于类别的个数)输出的第 i i i…...
laravel distinct查询问题,laravel子查询写法
直接调用后,count查询会和实际查询的数据对不上,count还是查询全部数据,而实际的列表是去重的。 给distinct加上参数,比如去重的值的id,就加id。 另一种写法是使用group by id 子查询。 sql语句: selec…...
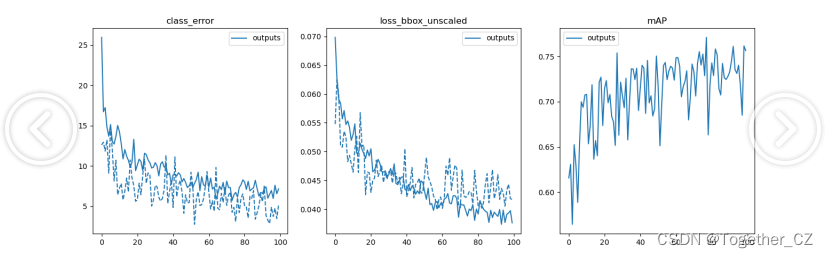
AI助力农作物自动采摘,基于DETR(DEtection TRansformer)开发构建作物生产场景下番茄采摘检测计数分析系统
去年十一那会无意间刷到一个视频展示的就是德国机械收割机非常高效自动化地24小时不间断地在超广阔的土地上采摘各种作物,专家设计出来了很多用于采摘不同农作物的大型机械,看着非常震撼,但是我们国内农业的发展还是相对比较滞后的࿰…...

C语言——字符串大小写互换
前言: 在C语言中,大小写字母相互转换是一个常见的操作。本文将详细介绍C语言中实现大小写字母相互转换的各种方法,并附上代码示例。 目录 一、使用tolower()和toupper()函数 二、使用位操作 三、使用字符串操作函数 一、使用tolower()和t…...

macOS的设置与常用软件(含IntelliJ IDEA 2023.3.2 Ultimate安装,SIP的关闭与开启)
目录 1 系统设置1.1 触控板1.2 键盘 2 软件篇2.1 [科学上网](https://justmysocks5.net/members/)2.1 [安装Chrome浏览器](https://www.google.cn/chrome/index.html)2.2 [安装utools](https://www.u.tools)2.3 [安装搜狗输入法](https://shurufa.sogou.com/)2.4 [安装snipaste…...
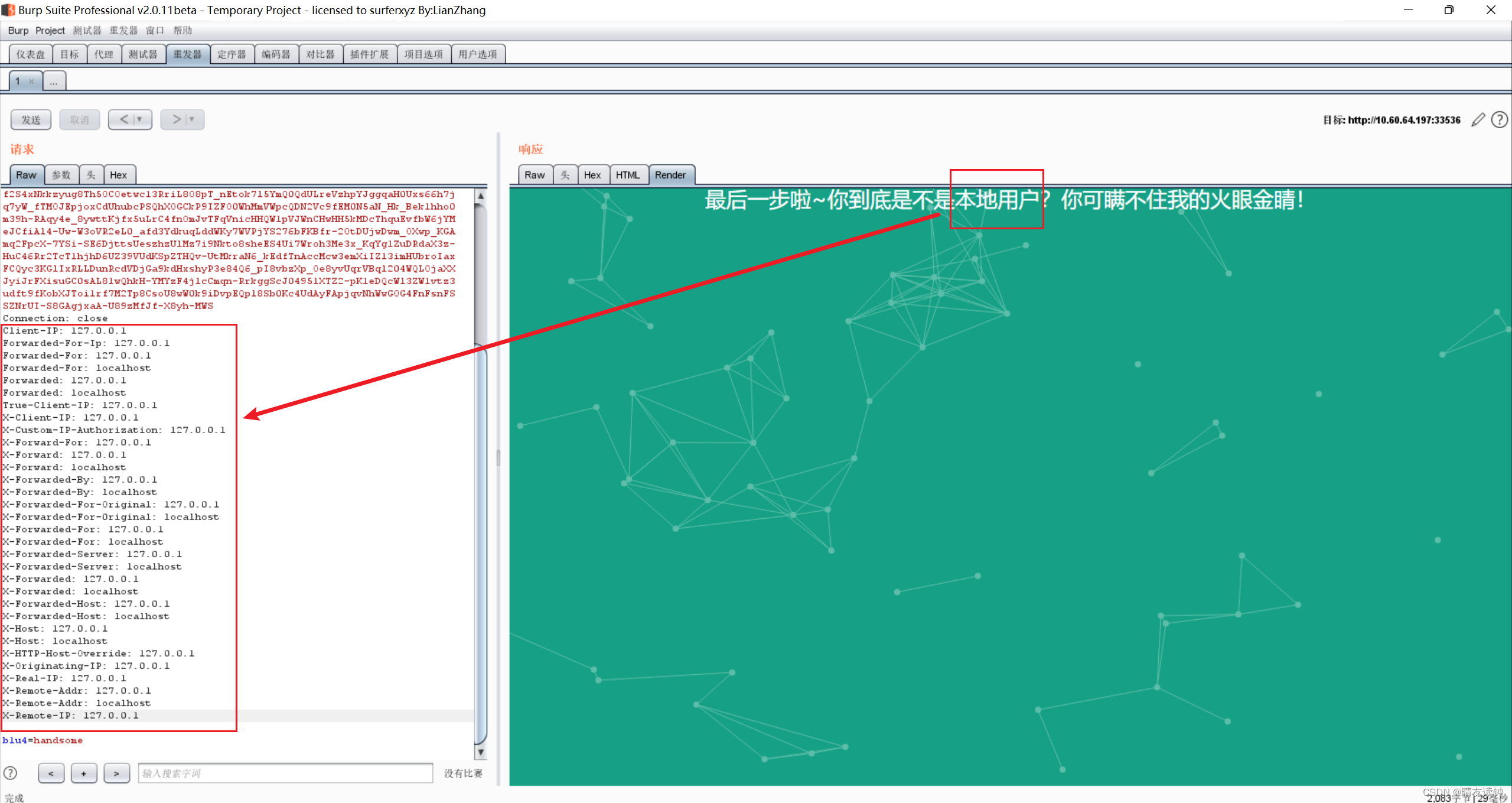
http伪造本地用户字段系列总结
本篇记录了http伪造本地用户的多条字段,便于快速解决题目 用法举例: 直接把伪造本地用户的多个字段复制到请求头中,光速解决部分字段被过滤的问题。 Client-IP: 127.0.0.1 Forwarded-For-Ip: 127.0.0.1 Forwarded-For: 127.0.0.1 Forwarded…...
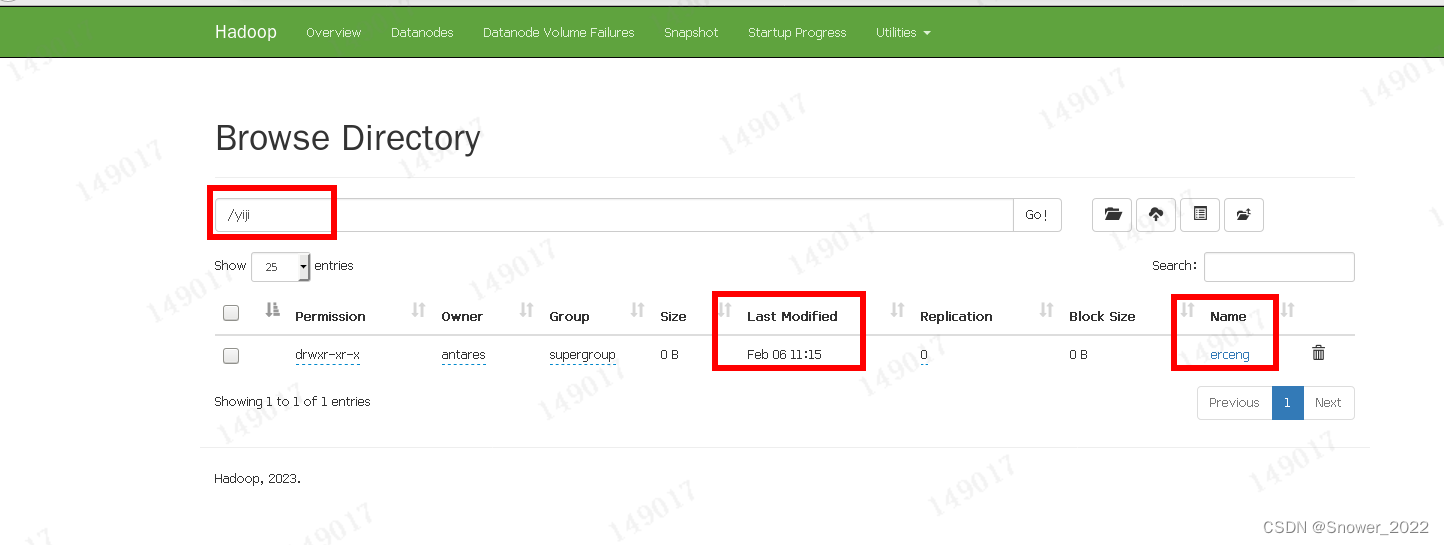
Hadoop-IDEA开发平台搭建
1.安装下载Hadoop文件 1)hadoop-3.3.5 将下载的文件保存到英文路径下,名称一定要短。否则容易出问题; 2)解压下载下来的文件,配置环境变量 3)我的电脑-属性-高级设置-环境变量 4.详细配置文件如下&#…...

block任务块、rescue和always、loop循环、role角色概述、role角色应用、ansible-vault、sudo提权、特殊的主机清单变量
任务块 可以通过block关键字,将多个任务组合到一起可以将整个block任务组,一起控制是否要执行 # 如果webservers组中的主机系统发行版是Rocky,则安装并启动nginx[rootpubserver ansible]# vim block1.yml---- name: block taskshosts: webse…...
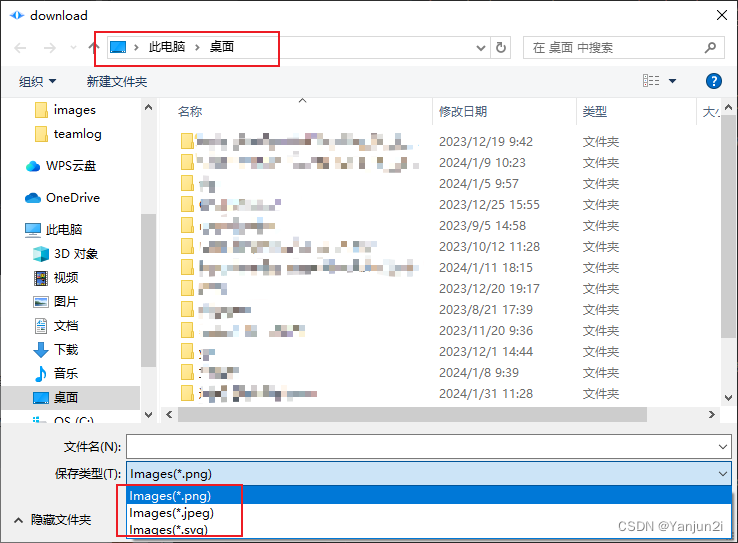
Qt:QFileDialog
目录 一、介绍 二、功能 三、具体事例 1、将某个界面保存为图片,后缀名可选PNG、JPEG、SVG等 一、介绍 QFileDialog提供了一个对话框,允许用户选择文件或者目录,也允许用户遍历文件系统,用以选择一个或多个文件或者目录。 QF…...

我的QQ编程学习群
欢迎大家加入我的QQ编程学习群。 群号:950365002 群里面有许多的大学生大佬,有编程上的疑惑可以随时问,也可以聊一些休闲的东西。 热烈欢迎大家加入!! 上限:150人。...

【C++】类与对象(四)——初始化列表|explicit关键字|static成员|友元|匿名对象
前言: 初始化列表,explicit关键字,static成员,友元,匿名对象 文章目录 一、构造函数的初始化列表1.1 构造函数体内赋值1.2 初始化列表 二、explicit关键字三、static成员四、友元4.1 友元函数4.2 友元类 五、内部类六、…...
ChatGPT高效提问—prompt常见用法
ChatGPT高效提问—prompt常见用法 1.1 角色扮演 prompt最为常见的用法是ChatGPT进行角色扮演。通常我们在和ChatGPT对话时,最常用的方式是一问一答,把ChatGPT当作一个单纯的“陪聊者”。而当我们通过prompt为ChatGPT赋予角色属性后,即使…...
使用vite创建vue+ts项目,整合常用插件(scss、vue-router、pinia、axios等)和配置
一、检查node版本 指令:node -v 为什么要检查node版本? Vite 需要 Node.js 版本 18,20。然而,有些模板需要依赖更高的 Node 版本才能正常运行,当你的包管理器发出警告时,请注意升级你的 Node 版本。 二、创…...
泛型、Trait 和生命周期(上)
目录 1、提取函数来减少重复 2、在函数定义中使用泛型 3、结构体定义中的泛型 4、枚举定义中的泛型 5、方法定义中的泛型 6、泛型代码的性能 每一门编程语言都有高效处理重复概念的工具。在 Rust 中其工具之一就是 泛型(generics)。泛型是具体类型…...

<网络安全>《18 数据安全交换系统》
1 概念 企业为了保护核心数据安全,都会采取一些措施,比如做网络隔离划分,分成了不同的安全级别网络,或者安全域,接下来就是需要建设跨网络、跨安全域的安全数据交换系统,将安全保障与数据交换功能有机整合…...
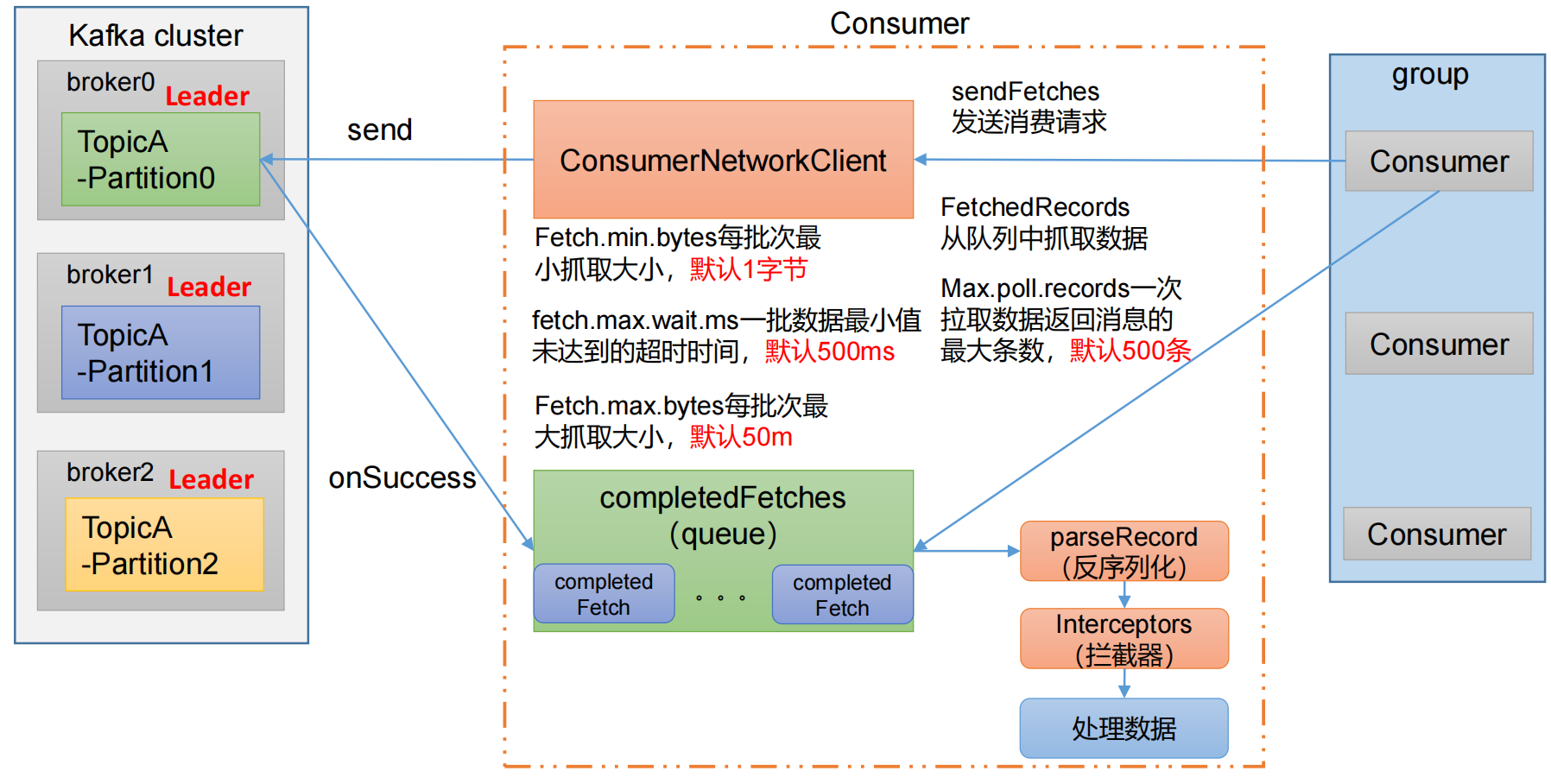
Kafka 生产调优
Kafka生产调优 文章目录 Kafka生产调优一、Kafka 硬件配置选择场景说明服务器台数选择磁盘选择内存选择CPU选择 二、Kafka Broker调优Broker 核心参数配置服役新节点/退役旧节点增加副本因子调整分区副本存储 三、Kafka 生产者调优生产者如何提高吞吐量数据可靠性数据去重数据乱…...
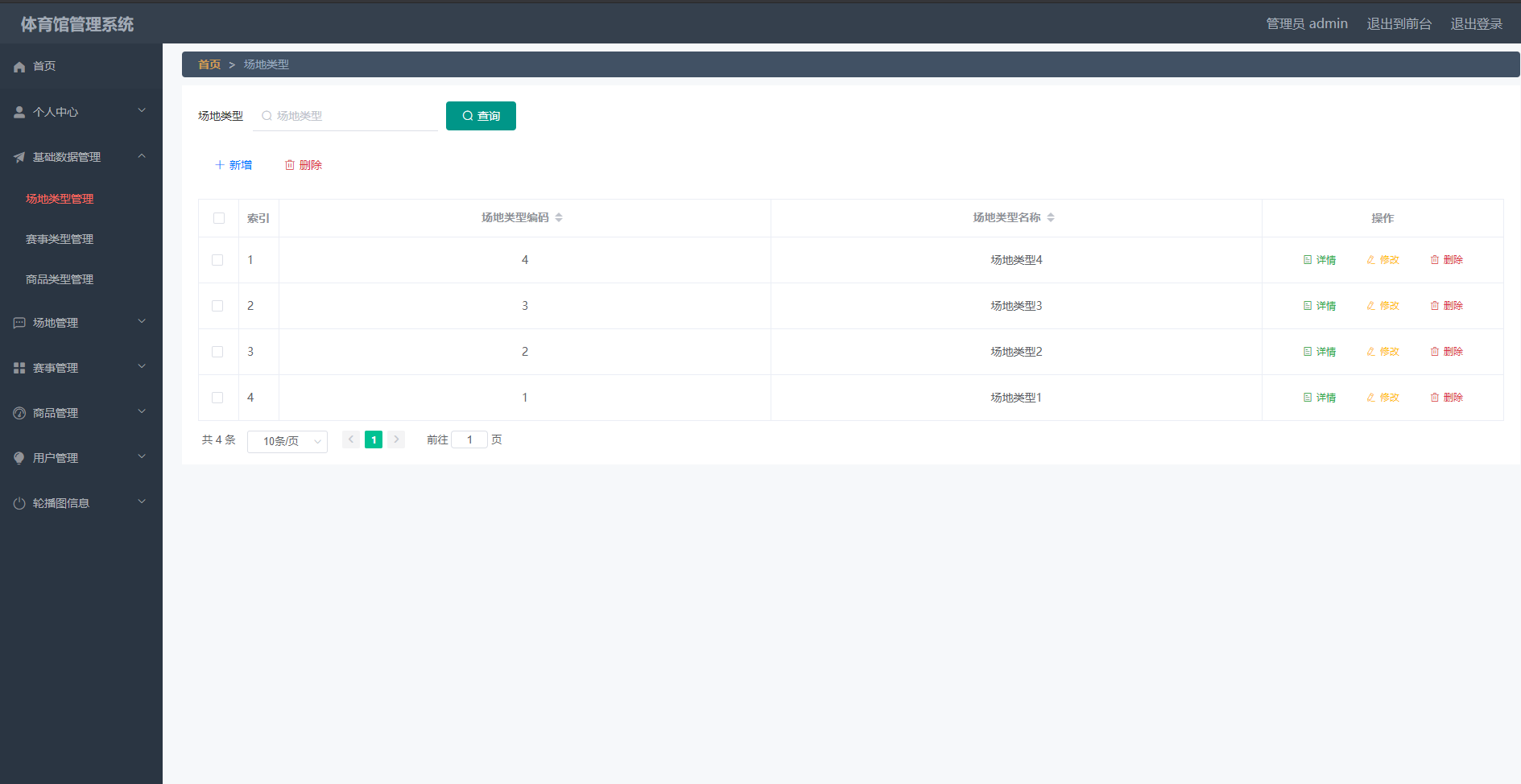
springboot162基于SpringBoot的体育馆管理系统的设计与实现
体育馆管理系统 摘 要 现代经济快节奏发展以及不断完善升级的信息化技术,让传统数据信息的管理升级为软件存储,归纳,集中处理数据信息的管理方式。本体育馆管理系统就是在这样的大环境下诞生,其可以帮助管理者在短时间内处理完毕…...

Interpolator:在Android中方便使用一些常见的CubicBezier贝塞尔曲线动画效果
说明 方便在Android中使用Interpolator一些常见的CubicBezier贝塞尔曲线动画效果。 示意图如下 import android.view.animation.Interpolator import androidx.core.view.animation.PathInterpolatorCompat/*** 参考* android https://yisibl.github.io/cubic-bezier* 实现常…...
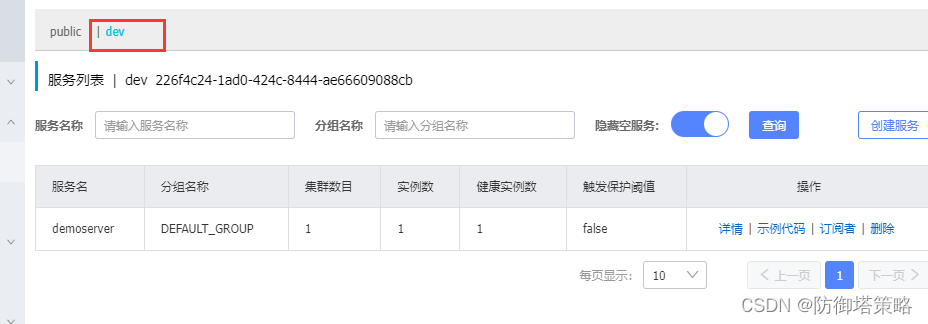
Nacos安装,服务注册,负载均衡配置,权重配置以及环境隔离
1. 安装 首先从官网下载 nacos 安装包,注意是下载 nacos-server Nacos官网 | Nacos 官方社区 | Nacos 下载 | Nacos 下载完毕后,解压找到文件夹bin,文本打开startup.cmd 修改配置如下 然后双击 startup.cmd 启动 nacos服务,默认…...

Vue3导出数据为txt文件
在Vue3中,可以通过使用Blob对象以及URL.createObjectURL()方法导出txt文档。 首先,你需要在Vue组件中创建一个方法来生成txt文档的内容。 //res.value.code 数据源 //type:格式设置 //form.name是下载文件的自定义名字 const downLoad ()&…...

铭豹扩展坞 USB转网口 突然无法识别解决方法
当 USB 转网口扩展坞在一台笔记本上无法识别,但在其他电脑上正常工作时,问题通常出在笔记本自身或其与扩展坞的兼容性上。以下是系统化的定位思路和排查步骤,帮助你快速找到故障原因: 背景: 一个M-pard(铭豹)扩展坞的网卡突然无法识别了,扩展出来的三个USB接口正常。…...

日语AI面试高效通关秘籍:专业解读与青柚面试智能助攻
在如今就业市场竞争日益激烈的背景下,越来越多的求职者将目光投向了日本及中日双语岗位。但是,一场日语面试往往让许多人感到步履维艰。你是否也曾因为面试官抛出的“刁钻问题”而心生畏惧?面对生疏的日语交流环境,即便提前恶补了…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

【大模型RAG】Docker 一键部署 Milvus 完整攻略
本文概要 Milvus 2.5 Stand-alone 版可通过 Docker 在几分钟内完成安装;只需暴露 19530(gRPC)与 9091(HTTP/WebUI)两个端口,即可让本地电脑通过 PyMilvus 或浏览器访问远程 Linux 服务器上的 Milvus。下面…...

QT: `long long` 类型转换为 `QString` 2025.6.5
在 Qt 中,将 long long 类型转换为 QString 可以通过以下两种常用方法实现: 方法 1:使用 QString::number() 直接调用 QString 的静态方法 number(),将数值转换为字符串: long long value 1234567890123456789LL; …...

全志A40i android7.1 调试信息打印串口由uart0改为uart3
一,概述 1. 目的 将调试信息打印串口由uart0改为uart3。 2. 版本信息 Uboot版本:2014.07; Kernel版本:Linux-3.10; 二,Uboot 1. sys_config.fex改动 使能uart3(TX:PH00 RX:PH01),并让boo…...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

使用 SymPy 进行向量和矩阵的高级操作
在科学计算和工程领域,向量和矩阵操作是解决问题的核心技能之一。Python 的 SymPy 库提供了强大的符号计算功能,能够高效地处理向量和矩阵的各种操作。本文将深入探讨如何使用 SymPy 进行向量和矩阵的创建、合并以及维度拓展等操作,并通过具体…...

2025季度云服务器排行榜
在全球云服务器市场,各厂商的排名和地位并非一成不变,而是由其独特的优势、战略布局和市场适应性共同决定的。以下是根据2025年市场趋势,对主要云服务器厂商在排行榜中占据重要位置的原因和优势进行深度分析: 一、全球“三巨头”…...

LLMs 系列实操科普(1)
写在前面: 本期内容我们继续 Andrej Karpathy 的《How I use LLMs》讲座内容,原视频时长 ~130 分钟,以实操演示主流的一些 LLMs 的使用,由于涉及到实操,实际上并不适合以文字整理,但还是决定尽量整理一份笔…...
