区间dp 笔记
区间dp一般是先枚举区间长度,再枚举左端点,再枚举分界点,时间复杂度为
环形石子合并
将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。
规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该次合并的得分。
请编写一个程序,读入堆数 n 及每堆的石子数,并进行如下计算:
- 选择一种合并石子的方案,使得做 n−1 次合并得分总和最大。
- 选择一种合并石子的方案,使得做 n−11 次合并得分总和最小。
输入格式
第一行包含整数 n,表示共有 n 堆石子。
第二行包含 n 个整数,分别表示每堆石子的数量。
输出格式
输出共两行:
第一行为合并得分总和最小值,
第二行为合并得分总和最大值。
数据范围
1≤n≤200
输入样例:
4
4 5 9 4
输出样例:
43
54考了把环拆成链,把两个数组拼在一起可以达成 类环 的效果
比如 1 2 3 4 1 2 3 4
环可以是[1 2 3 4] [2 3 4 1] [3 4 1 2] [4 1 2 3]
这样就可以在石子合并的基础上增加微量时间复杂度的情况下做这道题了
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef long long ll;
typedef pair<ll, int> PII;const int N = 410;int n;
int w[N], s[N];
int f[N][N], g[N][N];int main()
{IOScin >> n;for(int i = 1; i <= n; i ++){cin >> w[i];w[i + n] = w[i];}for(int i = 1; i <= n + n; i ++){s[i] = s[i - 1] + w[i];}memset(f, 0x3f, sizeof f);memset(g, -0x3f, sizeof g);for(int len = 1; len <= n; len ++){for(int l = 1; l + len - 1 <= n + n; l ++){int r = l + len - 1;if(len == 1){f[l][r] = g[l][r] = 0;continue;}for(int k = l; k < r; k ++){f[l][r] = min(f[l][r], f[l][k] + f[k + 1][r] + s[r] - s[l - 1]);g[l][r] = max(g[l][r], g[l][k] + g[k + 1][r] + s[r] - s[l - 1]);}}}int maxn = -2e9, minx = 2e9;for(int i = 1; i <= n; i ++){maxn = max(maxn, g[i][i + n - 1]);minx = min(minx, f[i][i + n - 1]);}cout << minx << endl;cout << maxn;return 0;
} 能量项链
在 Mars 星球上,每个 Mars 人都随身佩带着一串能量项链,在项链上有 N 颗能量珠。
能量珠是一颗有头标记与尾标记的珠子,这些标记对应着某个正整数。
并且,对于相邻的两颗珠子,前一颗珠子的尾标记一定等于后一颗珠子的头标记。
因为只有这样,通过吸盘(吸盘是 Mars 人吸收能量的一种器官)的作用,这两颗珠子才能聚合成一颗珠子,同时释放出可以被吸盘吸收的能量。
如果前一颗能量珠的头标记为 m,尾标记为 r,后一颗能量珠的头标记为 r,尾标记为 n,则聚合后释放的能量为 m×r×n(Mars 单位),新产生的珠子的头标记为 m,尾标记为 n。
需要时,Mars 人就用吸盘夹住相邻的两颗珠子,通过聚合得到能量,直到项链上只剩下一颗珠子为止。
显然,不同的聚合顺序得到的总能量是不同的,请你设计一个聚合顺序,使一串项链释放出的总能量最大。
例如:设 N=4,4 颗珠子的头标记与尾标记依次为 (2,3)(3,5)(5,10)(10,2)。
我们用记号 ⊕⊕ 表示两颗珠子的聚合操作,(j⊕k) 表示第 j,k 两颗珠子聚合后所释放的能量。则
第 4、1 两颗珠子聚合后释放的能量为:(4⊕1)=10×2×3=60。
这一串项链可以得到最优值的一个聚合顺序所释放的总能量为 ((4⊕1)⊕2)⊕3)=10×2×3+10×3×5+10×5×10=710。
输入格式
输入的第一行是一个正整数 N,表示项链上珠子的个数。
第二行是 N 个用空格隔开的正整数,所有的数均不超过 1000,第 i 个数为第 i 颗珠子的头标记,当 i<N 时,第 i 颗珠子的尾标记应该等于第 i+1 颗珠子的头标记,第 N 颗珠子的尾标记应该等于第 1 颗珠子的头标记。
至于珠子的顺序,你可以这样确定:将项链放到桌面上,不要出现交叉,随意指定第一颗珠子,然后按顺时针方向确定其他珠子的顺序。
输出格式
输出只有一行,是一个正整数 E,为一个最优聚合顺序所释放的总能量。
数据范围
4≤N≤100,
1≤E≤2.1×1e9
输入样例:
4
2 3 5 10
输出样例:
710和上一题几乎一模一样
可以先枚举长度,再枚举首位端点,再枚举连接点
我写的代码不太一样,但结果都是一样的
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef long long ll;
typedef pair<ll, int> PII;const int N = 210;int n;
int w[N];
ll f[N][N];int main()
{IOScin >> n;for(int i = 1; i <= n; i ++){cin >> w[i];w[i + n] = w[i];}memset(f, -0x3f, sizeof f);for(int len = 1; len <= n; len ++){for(int l = 1; l + len - 1 <= n + n; l ++){int r = l + len - 1;if(len == 1){f[l][r] = 0;continue;}for(int k = l; k < r; k ++){f[l][r] = max(f[l][r], f[l][k] + f[k + 1][r] + w[l] * w[k + 1] * w[r + 1]);}}}ll ans = -2e18;for(int i = 1; i <= n; i ++){ans = max(ans, f[i][i + n - 1]);}cout << ans;return 0;
} 加分二叉树
设一个 n 个节点的二叉树 tree 的中序遍历为(1,2,3,…,n),其中数字 1,2,3,…,n 为节点编号。
每个节点都有一个分数(均为正整数),记第 i 个节点的分数为 di,tree 及它的每个子树都有一个加分,任一棵子树 subtree(也包含 tree 本身)的加分计算方法如下:
subtree的左子树的加分 × subtree的右子树的加分 + subtree的根的分数
若某个子树为空,规定其加分为 1。
叶子的加分就是叶节点本身的分数,不考虑它的空子树。
试求一棵符合中序遍历为(1,2,3,…,n)且加分最高的二叉树 tree。
要求输出:
(1)tree的最高加分
(2)tree的前序遍历
输入格式
第 1 行:一个整数 n,为节点个数。
第 2 行:n 个用空格隔开的整数,为每个节点的分数(0<分数<100)。
输出格式
第 1 行:一个整数,为最高加分(结果不会超过int范围)。
第 2 行:n 个用空格隔开的整数,为该树的前序遍历。如果存在多种方案,则输出字典序最小的方案。
数据范围
n<30
输入样例:
5
5 7 1 2 10
输出样例:
145
3 1 2 4 5中序遍历一个数左边都是左子树的部分,一个数右边都是右子树的部分
所以可以用f[l, r]表示[l, r]区间内所有子树的最大值,去枚举每个点当根节点
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef long long ll;
typedef pair<ll, int> PII;const int N = 40;int n;
int w[N];
int f[N][N], g[N][N];void dfs(int l, int r)
{if(l > r)return;int t = g[l][r];cout << t << ' ';dfs(l, t - 1);dfs(t + 1, r);
}int main()
{IOScin >> n;for(int i = 1; i <= n; i ++)cin >> w[i];for(int len = 1; len <= n; len ++){for(int l = 1; l + len - 1 <= n; l ++){int r = l + len - 1;if(len == 1){f[l][r] = w[l];g[l][r] = l;continue;}for(int k = l; k <= r; k ++){int left = k == l ? 1 : f[l][k - 1];int right = k == r ? 1 : f[k + 1][r];int score = left * right + w[k];if(f[l][r] < score){f[l][r] = score;g[l][r] = k;}}}}cout << f[1][n] << endl;dfs(1, n);return 0;
}凸多边形的划分
给定一个具有 N 个顶点的凸多边形,将顶点从 1 至 N 标号,每个顶点的权值都是一个正整数。
将这个凸多边形划分成 N−2 个互不相交的三角形,对于每个三角形,其三个顶点的权值相乘都可得到一个权值乘积,试求所有三角形的顶点权值乘积之和至少为多少。
输入格式
第一行包含整数 N,表示顶点数量。
第二行包含 N个整数,依次为顶点 1 至顶点 N 的权值。
输出格式
输出仅一行,为所有三角形的顶点权值乘积之和的最小值。
数据范围
N≤50,
数据保证所有顶点的权值都小于1e9
输入样例:
5
121 122 123 245 231
输出样例:
12214884可以发现每条边只会参与一个三角形的构成
以1-n这条边为底,共有n-2种选法,设选了k这个点为顶点,那左边1~k和右面k~n两个区域明显是相互独立的,这就构成了区间dp的基础
枚举选顶点是哪个即可
这题虽然也是环但不需要拼起来,因为每个边只参与一次,选1 - n还是选2 - n+1都是一样的
另外需要用到高精度,可以先当成不需要高精度的写出来,再改成高精度,这样轻松一点
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef long long ll;
typedef pair<ll, int> PII;const int N = 55, M = 35, INF = 2e9;int n;
int w[N];
ll f[N][N][M];//f[l,r]表示以l、r两点为边,以中间的一个顶点作为分界线 void add(ll a[], ll b[])
{ll tmp[M] = {0};ll t = 0;for(int i = 0; i < M; i ++){t += a[i] + b[i];tmp[i] = t % 10;t /= 10;}memcpy(a, tmp, sizeof tmp);
}void mul(ll a[], ll b)
{ll tmp[M] = {0};ll t = 0;for(int i = 0; i < M; i ++){t += a[i] * b;tmp[i] = t % 10;t /= 10;}memcpy(a, tmp, sizeof tmp);
}int cmp(ll a[], ll b[])
{for(int i = M - 1; i >= 0; i --){if(a[i] > b[i])return 1;if(a[i] < b[i])return -1;}return 0;
}void print(ll a[])
{ll t = M - 1;while(t && !a[t])t --;for(int i = t; i >= 0; i --)cout << a[i];cout << endl;
}int main()
{IOScin >> n;for(int i = 1; i <= n; i ++)cin >> w[i];ll tmp[M];for(int len = 3; len <= n; len ++){for(int l = 1; l + len - 1 <= n; l ++){int r = l + len - 1;//f[l][r] = INF;f[l][r][M - 1] = 1;for(int k = l + 1; k < r; k ++){memset(tmp, 0, sizeof tmp);tmp[0] = w[l];mul(tmp, w[r]);mul(tmp, w[k]);add(tmp, f[l][k]);add(tmp, f[k][r]);if(cmp(tmp, f[l][r]) < 0){memcpy(f[l][r], tmp, sizeof tmp);}//f[l][r] = min(f[l][r], f[l][k] + f[k][r] + w[l] * w[r] * w[k]);}}}//cout << f[1][n];print(f[1][n]);return 0;
}棋盘分割
将一个 8×8 的棋盘进行如下分割:将原棋盘割下一块矩形棋盘并使剩下部分也是矩形,再将剩下的部分继续如此分割,这样割了 (n−1)次后,连同最后剩下的矩形棋盘共有 n块矩形棋盘。(每次切割都只能沿着棋盘格子的边进行)
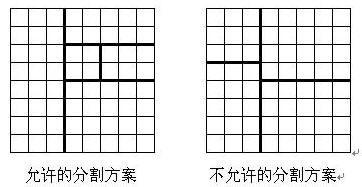
原棋盘上每一格有一个分值,一块矩形棋盘的总分为其所含各格分值之和。
现在需要把棋盘按上述规则分割成 n 块矩形棋盘,并使各矩形棋盘总分的均方差最小。
均方差
![]()
,其中平均值
![]()
,xi 为第 i 块矩形棋盘的总分。
请编程对给出的棋盘及 n,求出均方差的最小值。
输入格式
第 1 行为一个整数 n。
第 2 行至第 9 行每行为 8 个小于 100 的非负整数,表示棋盘上相应格子的分值。每行相邻两数之间用一个空格分隔。
输出格式
输出最小均方差值(四舍五入精确到小数点后三位)。
数据范围
1<n<15
输入样例:
3
1 1 1 1 1 1 1 3
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0
1 1 1 1 1 1 0 3
输出样例:
1.633f[x1][y1][x2][y1][k]表示左上角的点为(x1,y1),右下角的点为(x2,y2),这块区域要被分位k个点,表示均方差平方的最小值
由题可得n确定后平均值X也能确定
枚举时考虑横着切还是竖着切,切的时候考虑是留上边还是下边、左边还是右边
#include<bits/stdc++.h>
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define endl '\n'using namespace std;typedef long long ll;
typedef pair<ll, int> PII;const int N = 9, M = 15, INF = 2e9;int n, m = 8;
int s[N][N];
double f[N][N][N][N][M];
double X;double get(int x1, int y1, int x2, int y2)
{double res = s[x2][y2] - s[x1 - 1][y2] - s[x2][y1 - 1] + s[x1 - 1][y1 - 1] - X;return res * res / n;
}double dp(int x1, int y1, int x2, int y2, int k)
{double &v = f[x1][y1][x2][y2][k];if(v >= 0)return v;if(k == 1)return get(x1, y1, x2, y2);v = INF;for(int i = x1; i < x2; i ++){v = min(v, dp(x1, y1, i, y2, k - 1) + get(i + 1, y1, x2, y2));v = min(v, get(x1, y1, i, y2) + dp(i + 1, y1, x2, y2, k - 1));}for(int j = y1; j < y2; j ++){v = min(v, dp(x1, y1, x2, j, k - 1) + get(x1, j + 1, x2, y2));v = min(v, get(x1, y1, x2, y2) + dp(x1, j + 1, x2, y2, k - 1)); }return v;
}int main()
{//IOScin >> n;for(int i = 1; i <= m; i ++){for(int j = 1; j <= m; j ++){cin >> s[i][j];s[i][j] += s[i - 1][j] + s[i][j - 1] - s[i - 1][j - 1];}}X = (double)s[m][m] / n;memset(f, -1, sizeof f);double t = dp(1, 1, m, m, n);printf("%.3lf", sqrt(t));return 0;
}相关文章:
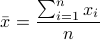
区间dp 笔记
区间dp一般是先枚举区间长度,再枚举左端点,再枚举分界点,时间复杂度为 环形石子合并 将 n 堆石子绕圆形操场排放,现要将石子有序地合并成一堆。 规定每次只能选相邻的两堆合并成新的一堆,并将新的一堆的石子数记做该…...
MySQL-SQL优化
文章目录 1. SQL性能分析1.1 SQL执行频率1.2 慢查询日志1.3 profile详情1.4 explain 2. SQL优化2.1 Insert 优化2.2 Group By 优化2.3 Order By 优化2.4 Limit 优化2.5 Count() 优化2.6 Update 优化 3. 拓展3.1 请你说一下MySQL中的性能调优的方法?3.2 执行 SQL 响应…...

详细了解ref和reactive.
这几天看到好多文章标题都是类似于: 不用 ref 的 xx 个理由不用 reactive 的 xx 个理由历数 ref 的 xx 宗罪 我就很不解,到底是什么原因导致有这两批人: 抵触 ref 的人抵触 reactive 的人 看了这些文章,我可以总结出他们的想法…...
使用Linux docker方式快速安装Plik并结合内网穿透实现公网访问
文章目录 1. Docker部署Plik2. 本地访问Plik3. Linux安装Cpolar4. 配置Plik公网地址5. 远程访问Plik6. 固定Plik公网地址7. 固定地址访问Plik 本文介绍如何使用Linux docker方式快速安装Plik并且结合Cpolar内网穿透工具实现远程访问,实现随时随地在任意设备上传或者…...

Redis Centos7 安装到启动
文章目录 安装Redis启动redis查看redis状况连接redis服务端 安装Redis 1.下载scl源 yum install centos-release-scl-rh2.下载redis yum install rh-redis5-redis 3. 创建软连接 1.cd /usr/bin 2. In -s /opt/rh/rh-redis5/root/usr/bin/redis-server ./redis-server 3. …...
「数据结构」二叉搜索树1:实现BST
🎇个人主页:Ice_Sugar_7 🎇所属专栏:Java数据结构 🎇欢迎点赞收藏加关注哦! 实现BST 🍉二叉搜索树的性质🍉实现二叉搜索树🍌插入🍌查找🍌删除 &am…...

可达鸭二月月赛——基础赛第六场(周五)题解,这次四个题的题解都在这一篇文章内,满满干货,含有位运算的详细用法介绍。
姓名 王胤皓 T1 题解 T1 题面 T1 思路 样例输入就是骗人的,其实直接输出就可以了,输出 Hello 2024,注意,中间有一个空格! T1 代码 #include<bits/stdc.h> using namespace std; #define ll long long int …...
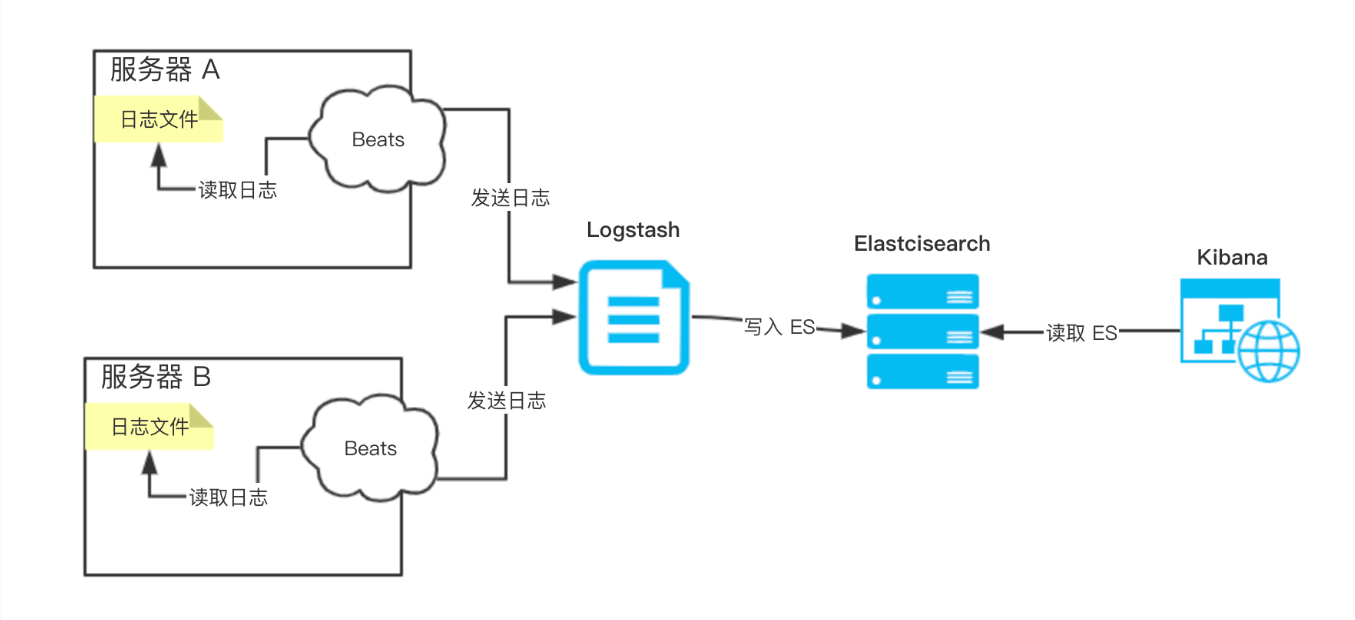
ELFK日志采 - QuickStart
文章目录 架构选型ELKEFLK ElasticsearchES集群搭建常用命令 Filebeat功能介绍安装步骤Filebeat配置详解filebeat常用命令 Logstash功能介绍安装步骤Input插件Filter插件Grok Filter 插件Mutate Filter 插件常见的插件配置选项:Mutate Filter配置案例: O…...
微信小程序的图片色彩分析,窃取网络图片的主色调
1、安装 Mini App Color Thief 包 包括下载包,简单使用都有,之前写了,这里就不写了 网址:微信小程序的图片色彩分析,窃取主色调,调色板-CSDN博客 2、 问题和解决方案 问题:由于我们的窃取图片的…...

Leetcode 121 买卖股票的最佳时机
题意理解: 给定一个数组 prices ,它的第 i 个元素 prices[i] 表示一支给定股票第 i 天的价格。 你只能选择 某一天 买入这只股票,并选择在 未来的某一个不同的日子 卖出该股票。设计一个算法来计算你所能获取的最大利润。 返回你可以从这笔交…...

SQL语言复习-----1
1,前言 SQL是计算机的一门基础语言,无论在开发还是数据库管理上都是非常重要,最近总结归纳了一下相关知识,记录如下。 2,归纳 SQL是结构化查询语言。 关系数据库有三级模式结构。 基本表和视图一样都是关系。 举例…...
爬虫2—用爬虫爬取壁纸(想爬多少张爬多少张)
先看效果图: 我这个是爬了三页的壁纸60张。 上代码了。 import requests import re import os from bs4 import BeautifulSoupcount0 img_path "./壁纸图片/"#指定保存地址 if not os.path.exists(img_path):os.mkdir(img_path) headers{ "User-Ag…...

学习Android的第九天
目录 Android Button 按钮 基本的按钮 StateListDrawable 范例 使用颜色值绘制圆角按钮 自制水波纹效果 Android ImageButton 图片按钮 ImageButton 不同状态下的 ImageButton Android RadioButton 单选按钮 RadioButton 获得选中的值 Android Button 按钮 在 And…...

课时21:内置变量_脚本相关
2.4.1 脚本相关 学习目标 这一节,我们从 基础知识、简单实践、小结 三个方面来学习 基础知识 脚本相关的变量解析 序号变量名解析1$0获取当前执行的shell脚本文件名2$n获取当前执行的shell脚本的第n个参数值,n1…9,当n为0时表示脚本的文…...

ubuntu22.04@laptop OpenCV Get Started: 006_annotating_images
ubuntu22.04laptop OpenCV Get Started: 006_annotating_images 1. 源由2. line/circle/rectangle/ellipse/text 应用Demo3 image_annotation3.1 C应用Demo3.2 Python应用Demo3.3 重点过程分析3.3.1 划线3.3.2 画圆3.3.3 矩形3.3.4 椭圆3.3.5 文字 4. 总结5. 参考资料 1. 源由 …...

【制作100个unity游戏之23】实现类似七日杀、森林一样的生存游戏10(附项目源码)
本节最终效果演示 文章目录 本节最终效果演示系列目录前言快捷栏绘制UI代码控制快捷列表信息 源码完结 系列目录 前言 欢迎来到【制作100个Unity游戏】系列!本系列将引导您一步步学习如何使用Unity开发各种类型的游戏。在这第23篇中,我们将探索如何制作…...
uniapp vue3怎么调用uni-popup组件的this.$refs.message.open() ?
vue2代码 <!-- 提示信息弹窗 --><uni-popup ref"message" type"message"><uni-popup-message :type"msgType" :message"messageText" :duration"2000"></uni-popup-message></uni-popup>typ…...

【深度学习:语义分割】语义分割简介
【深度学习:语义分割】语义分割简介 什么是图像分割?了解语义分割数据采集语义分割的深度学习实现全卷积网络上采样跳跃连接U-NetDeepLab多尺度物体检测金字塔场景解析网络(PSPNet) 语义分割的应用医学影像自动驾驶汽车农业图片处…...

前端开发_AJAX基本使用
AJAX概念 AJAX是异步的JavaScript和XML(Asynchronous JavaScript And XML)。 简单点说,就是使用XMLHttpRequest对象与服务器通信。 它可以使用JSON,XML,HTML和text文本等格式发送和接收数据。 AJAX最吸引人的就是它的“异步"特性&am…...
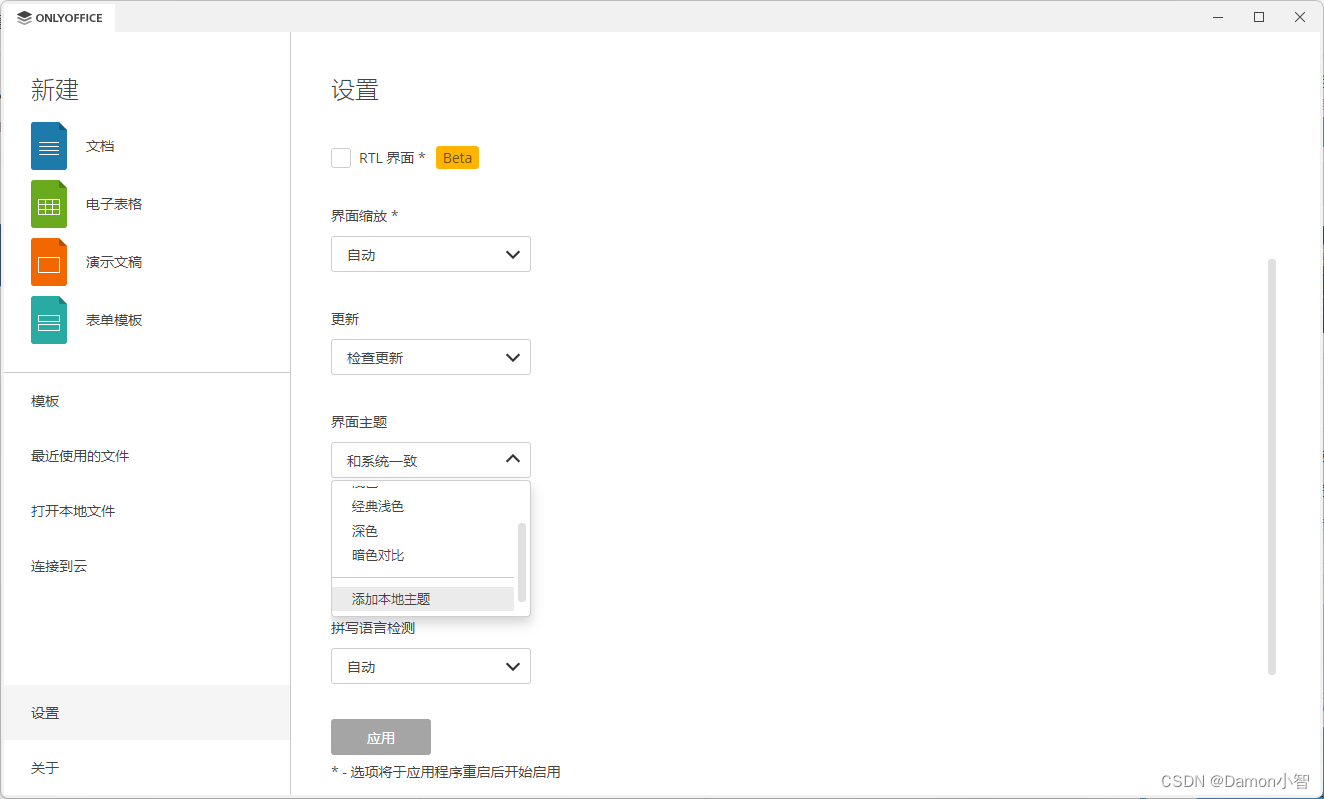
OnlyOffice-8.0版本深度测评
OnlyOffice 是一套全面的开源办公协作软件,不断演进的 OnlyOffice 8.0 版本为用户带来了一系列引人瞩目的新特性和功能改进。OnlyOffice 8.0 版本在功能丰富性、安全性和用户友好性上都有显著提升,为用户提供了更为强大、便捷和安全的文档处理和协作环境…...
)
rknn优化教程(二)
文章目录 1. 前述2. 三方库的封装2.1 xrepo中的库2.2 xrepo之外的库2.2.1 opencv2.2.2 rknnrt2.2.3 spdlog 3. rknn_engine库 1. 前述 OK,开始写第二篇的内容了。这篇博客主要能写一下: 如何给一些三方库按照xmake方式进行封装,供调用如何按…...

Unity3D中Gfx.WaitForPresent优化方案
前言 在Unity中,Gfx.WaitForPresent占用CPU过高通常表示主线程在等待GPU完成渲染(即CPU被阻塞),这表明存在GPU瓶颈或垂直同步/帧率设置问题。以下是系统的优化方案: 对惹,这里有一个游戏开发交流小组&…...

多场景 OkHttpClient 管理器 - Android 网络通信解决方案
下面是一个完整的 Android 实现,展示如何创建和管理多个 OkHttpClient 实例,分别用于长连接、普通 HTTP 请求和文件下载场景。 <?xml version"1.0" encoding"utf-8"?> <LinearLayout xmlns:android"http://schemas…...

vscode(仍待补充)
写于2025 6.9 主包将加入vscode这个更权威的圈子 vscode的基本使用 侧边栏 vscode还能连接ssh? debug时使用的launch文件 1.task.json {"tasks": [{"type": "cppbuild","label": "C/C: gcc.exe 生成活动文件"…...

深入理解JavaScript设计模式之单例模式
目录 什么是单例模式为什么需要单例模式常见应用场景包括 单例模式实现透明单例模式实现不透明单例模式用代理实现单例模式javaScript中的单例模式使用命名空间使用闭包封装私有变量 惰性单例通用的惰性单例 结语 什么是单例模式 单例模式(Singleton Pattern&#…...
Mobile ALOHA全身模仿学习
一、题目 Mobile ALOHA:通过低成本全身远程操作学习双手移动操作 传统模仿学习(Imitation Learning)缺点:聚焦与桌面操作,缺乏通用任务所需的移动性和灵活性 本论文优点:(1)在ALOHA…...

C#中的CLR属性、依赖属性与附加属性
CLR属性的主要特征 封装性: 隐藏字段的实现细节 提供对字段的受控访问 访问控制: 可单独设置get/set访问器的可见性 可创建只读或只写属性 计算属性: 可以在getter中执行计算逻辑 不需要直接对应一个字段 验证逻辑: 可以…...

华为OD机试-最短木板长度-二分法(A卷,100分)
此题是一个最大化最小值的典型例题, 因为搜索范围是有界的,上界最大木板长度补充的全部木料长度,下界最小木板长度; 即left0,right10^6; 我们可以设置一个候选值x(mid),将木板的长度全部都补充到x,如果成功…...

2.3 物理层设备
在这个视频中,我们要学习工作在物理层的两种网络设备,分别是中继器和集线器。首先来看中继器。在计算机网络中两个节点之间,需要通过物理传输媒体或者说物理传输介质进行连接。像同轴电缆、双绞线就是典型的传输介质,假设A节点要给…...

webpack面试题
面试题:webpack介绍和简单使用 一、webpack(模块化打包工具)1. webpack是把项目当作一个整体,通过给定的一个主文件,webpack将从这个主文件开始找到你项目当中的所有依赖文件,使用loaders来处理它们&#x…...
