最大子序和+旅行问题——单调队列
一、最大子序和
输入一个长度为 n 的整数序列,从中找出一段长度不超过 m 的连续子序列,使得子序列中所有数的和最大。
注意: 子序列的长度至少是 1。
输入
第一行输入两个整数 n,m (1 ≤ n,m ≤ 300000)。
第二行输入 n 个数,代表长度为 n 的整数序列。
同一行数之间用空格隔开。
输出
输出一个整数,代表该序列的最大子序和。
Input
6 4
1 -3 5 1 -2 3
Output
7
解析:
在长度不超过m的连续子序列,找到和最大的连续子序列。
集合按照终点的不同划分,划分成 n 个子集,答案就是不同子集的最大值。
假如,终点是 k 的连续子序列,它的最大和就是 max({a[k],a[k]+a[k-1],a[k]+a[k-1]+a[k-2],……,a[k]+…a[k-m+1]});
可以发现就是 s[k]-s[k-j] 的最大值,(其中1≤j≤m,s[N]是前缀和);
又因为终点 k 是确定不动的,这道题就转化成求在区间长度不超过 m 的 s[k-j]的最小值,典型的滑动窗口问题。
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=2e6+10;
int n,m;
int s[N];
int q[N];
void solve()
{cin>>n>>m;for (int i=1;i<=n;i++) cin>>s[i],s[i] +=s[i-1];int hh=0,tt=1; //最开始队列不空,有s[0]int ans=s[1];for (int i=1;i<=n;i++){if (hh<=tt&&i-q[hh]>m) hh++;ans=max(ans,s[i]-s[q[hh]]); //比较每个子集,更新答案while (hh<=tt&&s[q[tt]]>=s[i]) tt--;q[++tt]=i;}cout<<ans;
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}二、 旅行问题
John 打算驾驶一辆汽车周游一个环形公路。
公路上总共有 n 个车站,每站都有若干升汽油(有的站可能油量为零),每升油可以让汽车行驶一千米。
John 必须从某个车站出发,一直按顺时针(或逆时针)方向走遍所有的车站,并回到起点。
在一开始的时候,汽车内油量为零,John 每到一个车站就把该站所有的油都带上(起点站亦是如此),行驶过程中不能出现没有油的情况。
任务:判断以每个车站为起点能否按条件成功周游一周。
输入
第一行是一个整数 n (3 ≤ n ≤ 1e6),表示环形公路上的车站数;
接下来 n 行,每行两个整数 pi,di (0 ≤ pi ≤ 2e9,0 ≤ di ≤ 2e9),分别表示表示第 i 号车站的存油量和第 i 号车站到 顺时针方向 下一站的距离。
输出
输出共 n 行,如果从第 i 号车站出发,一直按顺时针(或逆时针)方向行驶,能够成功周游一圈,则在第 i 行输出 TAK,否则输出 NIE。
Input
5
3 1
1 2
5 2
0 1
5 4
Output
TAK
NIE
TAK
NIE
TAK

解析:
破链成环,可以根据顺时针和逆时针分开求;
下面先考虑顺时针的情况:
开一个数组存储的是 当前点的油量*100-到下一点的距离的前缀和 ;
而我们判断的是 当前点绕一圈,能否到达每一个点,就等价于 从当前点开始,到最后,每一个点的前缀和是否都大于 0 ;
而判断每个点的前缀和是否都大于0,就等价于判断最小值是否大于 0 ;
综上所述,就转化为求以每个点为起点,求在长度不超过 n 的数组的最小值是否大于0,即 区间[i,i+n-1]的最小值是否大于0,又转化成经典的滑动窗口问题!!!
(为什么要判断每个点的前缀和大于0? 如果能从起点到达当前点,那一定是之前每个站点的油量*1000之和-到达之前点的每段距离大于0,恰好就是这个新开数组能表达这种关系)
#include <bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
#define ios ios::sync_with_stdio(false),cin.tie(nullptr),cout.tie(nullptr);
int gcd(int a,int b) { return b? gcd(b,a%b) : a; }
typedef pair<int,int> PII;
const double PI=acos(-1.0);
const int N=2e6+10;
int n;
int o[N],d[N];
int s[N];
int q[N];
bool vis[N];
void solve()
{cin>>n;for (int i=1;i<=n;i++) cin>>o[i]>>d[i];for (int i=1;i<=n;i++) s[i+n]=s[i]=o[i]-d[i];for (int i=1;i<=2*n;i++) s[i] +=s[i-1];int hh=0,tt=0;q[0]=2*n+1;for (int i=2*n;i>=0;i--){if (hh<=tt&&q[hh]>i+n) hh++;if (i<n){if(s[q[hh]]-s[i]>=0) vis[i+1]=1;}while (hh<=tt&&s[q[tt]]>=s[i]) tt--;q[++tt]=i;}d[0]=d[n];for (int i=1;i<=n;i++) s[i+n]=s[i]=o[i]-d[i-1];for (int i=1;i<=2*n;i++) s[i] +=s[i-1];hh=0,tt=0;q[0]=0;for (int i=1;i<=2*n;i++){if (hh<=tt&&q[hh]<i-n) hh++;if (i>n){if (s[i]-s[q[hh]]>=0) vis[i-n]=1;}while (hh<=tt&&s[q[tt]]<=s[i]) tt--;q[++tt]=i;}for (int i=1;i<=n;i++){if (vis[i]) cout<<"TAK\n";else cout<<"NIE\n";}
}
signed main()
{ios;int T=1;//cin>>T;while (T--) solve();return 0;
}相关文章:

最大子序和+旅行问题——单调队列
一、最大子序和 输入一个长度为 n 的整数序列,从中找出一段长度不超过 m 的连续子序列,使得子序列中所有数的和最大。 注意: 子序列的长度至少是 1。 输入 第一行输入两个整数 n,m (1 ≤ n,m ≤ 300000)。 第二行输入 n 个数,代…...
Unity设备分级策略
Unity设备分级策略 前言 之前自己做的设备分级策略,在此做一个简单的记录和思路分享。希望能给大家带来帮助。 分级策略 根据拟定的评分标准,预生成部分已知机型的分级信息,且保存在包内;如果设备没有被评级过,则优…...

自己在开发AI应用的过程总结的 Prompt - 持续更新
自己在开发AI应用的过程总结的 Prompt - 持续更新 0. 引言1. 让模型以"中文"进行回复2. 控制模型仅输出"hi"3. 让模型"提供简单、清晰而具体的回答"4. 让模型"在最后说谢谢" 0. 引言 我想,我们多半有着相似的经历…...

STM32——OLED菜单
文章目录 一.补充二. 二级菜单代码 简介:首先在我的51 I2C里面有OLED详细讲解,本期代码从51OLED基础上移植过来的,可以先看完那篇文章,在看这个,然后按键我是用的定时器扫描不会堵塞程序,可以翻开我的文章有单独的定时…...
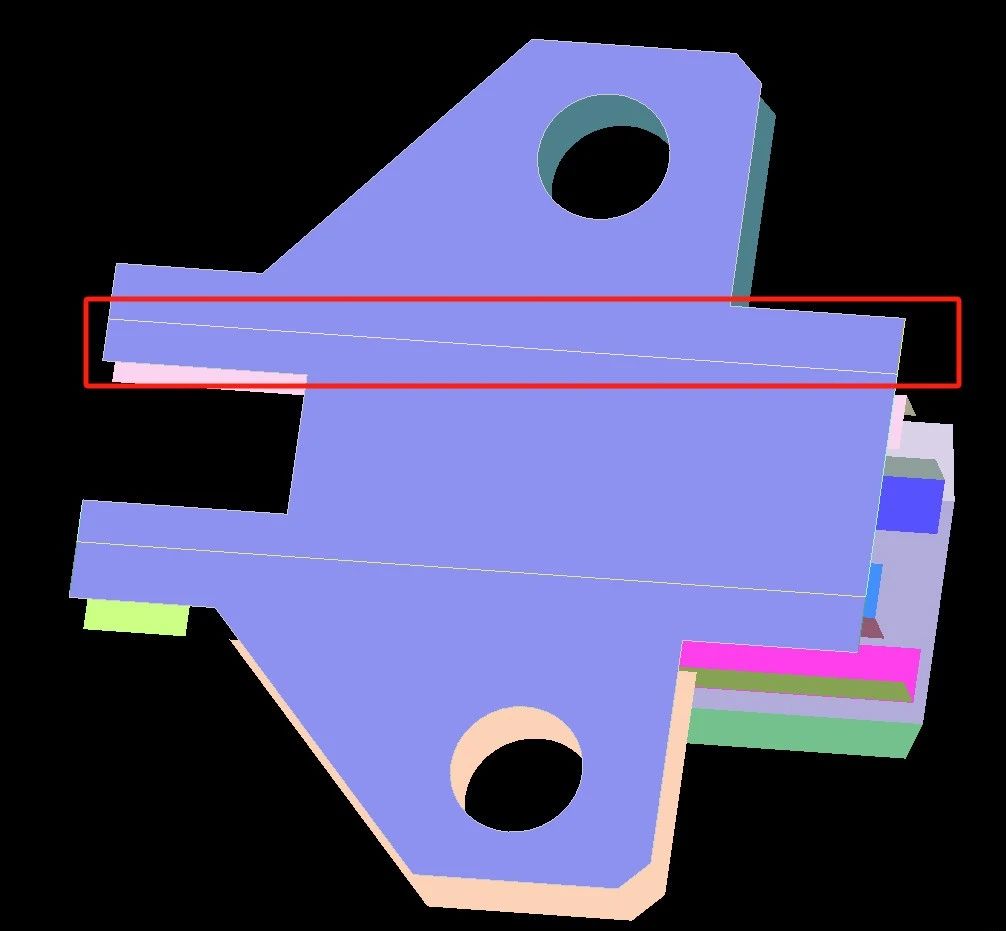
Open CASCADE学习|布尔运算后消除内部拓扑
在CAD建模中,布尔运算是一种逻辑运算方法,通过这种方法,可以创建、修改或组合几何对象。布尔运算主要包括并集(UNION)、交集(INTERSECT)和差集(SUBTRACT)三种运算。 并集…...
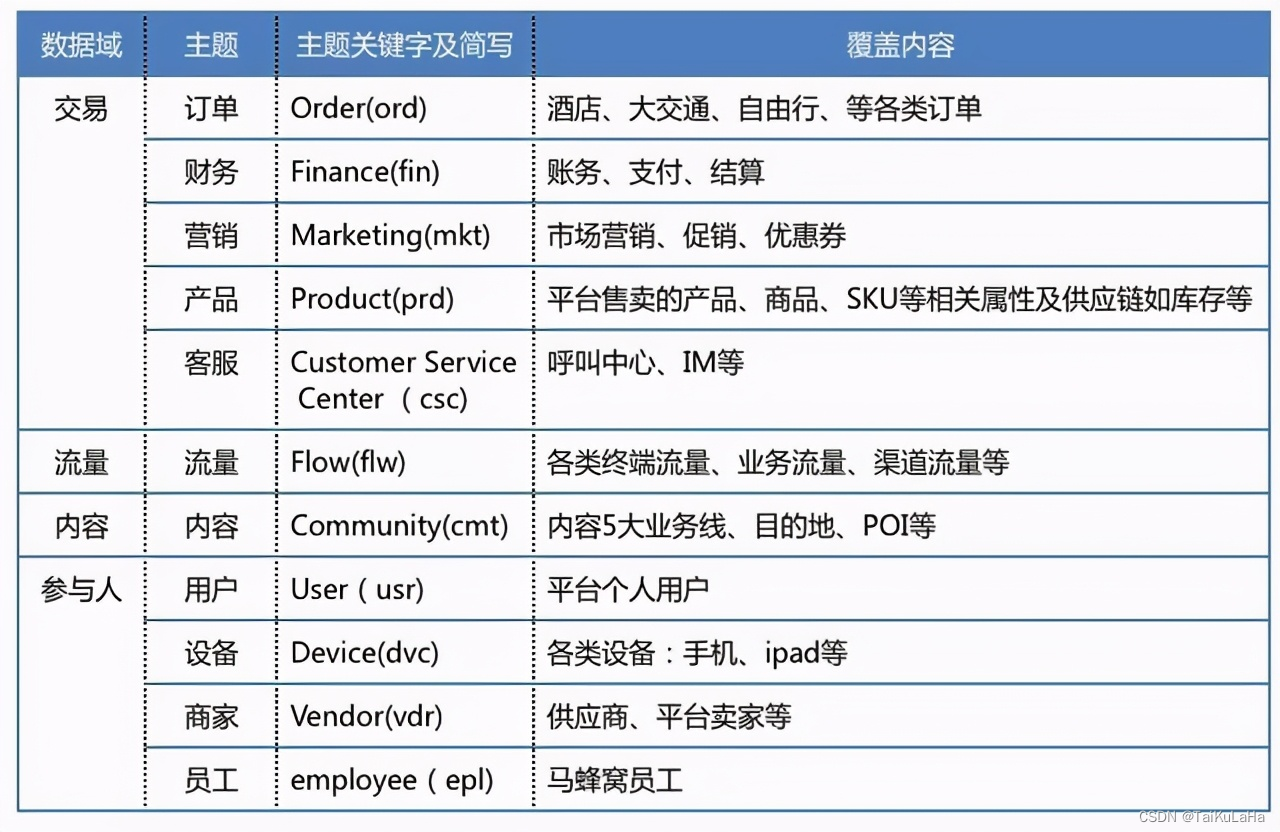
【数据仓库】主题域和数据域
数据域与主题域区别 https://www.cnblogs.com/datadance/p/16898254.html 数据域是自下而上,以业务数据视角来划分数据,一般进行完业务系统数据调研之后就可以进行数据域的划分。针对公共明细层(DWD)进行主题划分。主题域则自上而…...
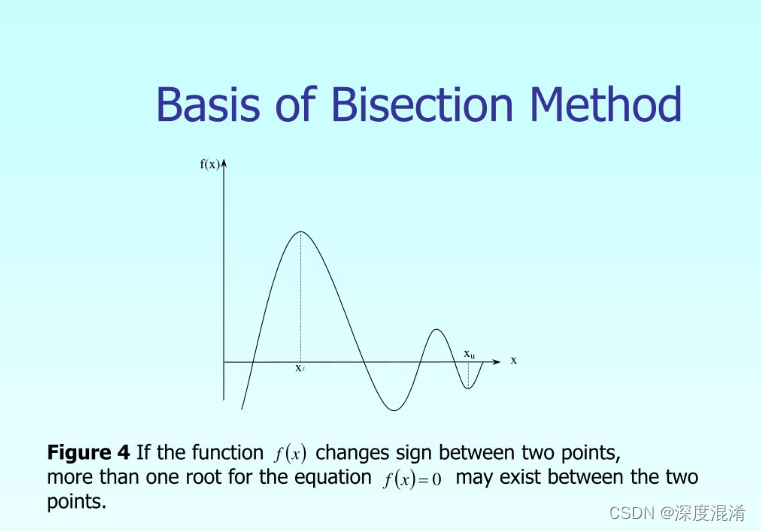
C#,二分法(Bisection Method)求解方程的算法与源代码
1 二分法 二分法是一种分治算法,是一种数学思维。 对于区间[a,b]上连续不断且f(a)f(b)<0的函数yf(x),通过不断地把函数f(x)的零点所在的区间…...

Portainer安装/快速上手
前置: 管理docker容器的工具 Portainer: Container Management Software for Kubernetes and Docker https://docs.portainer.io/v/ce-2.9/start/install/server/docker/linux 官网安装教程 Install Portainer CE with Docker on Linux - Portainer Documentat…...
恢复被.target勒索病毒加密的数据文件:拒绝向.target勒索病毒支付赎金
引言: 在当今数字时代,勒索病毒已成为网络安全领域的一大威胁,而.target勒索病毒是其中引起广泛关注的一种变种。本文将深入探讨.target勒索病毒的特点以及被其加密的数据文件恢复方法。数据的重要性不容小觑,您可添加我们的技术…...
【Linux网络编程六】服务器守护进程化Daemon
【Linux网络编程六】服务器守护进程化Daemon 一.背景知识:前台与后台二.相关操作三.Linux的进程间关系四.自成会话五.守护进程四步骤六.服务器守护进程化 一.背景知识:前台与后台 核心知识就是一个用户在启动Linux时,都会给一个session会话&a…...

MySQL之json数据操作
1 MySQL之JSON数据 总所周知,mysql5.7以上提供了一种新的字段格式json,大概是mysql想把非关系型和关系型数据库一口通吃,所以推出了这种非常好用的格式,这样,我们的很多基于mongoDB的业务都可以用mysql去实现了。当然…...
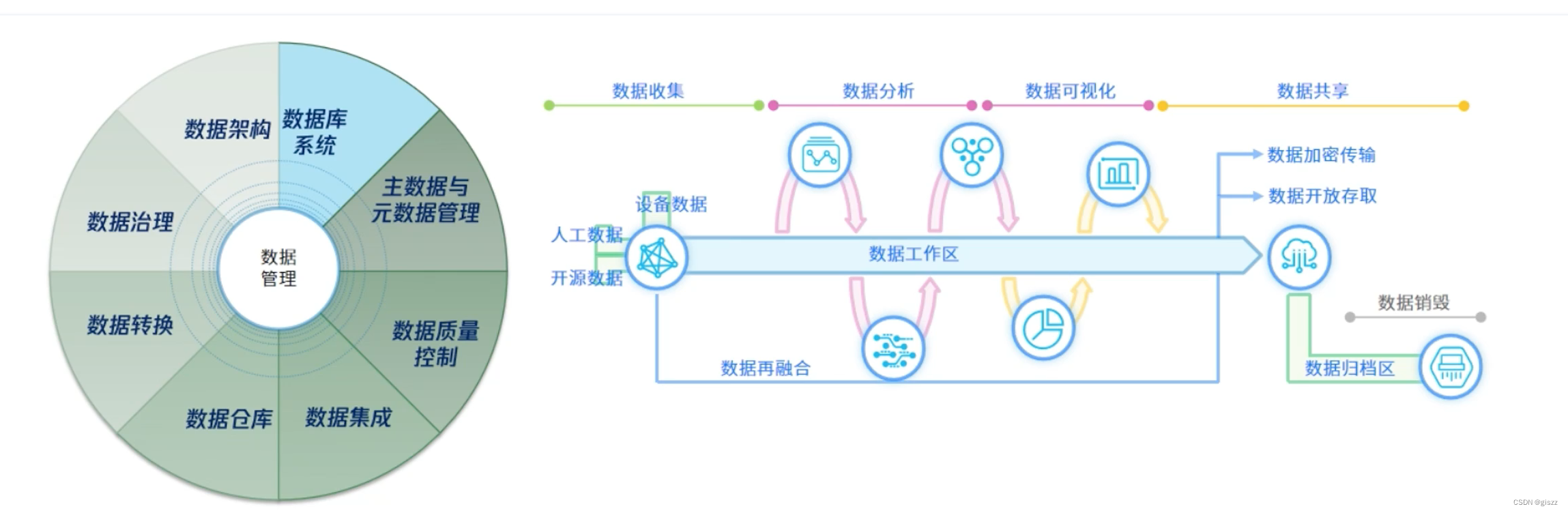
【大厂AI课学习笔记】【2.1 人工智能项目开发规划与目标】(5)数据管理
今天学习了数据管理,以及数据管理和数据治理的区别和联系。 数据管理:利用计算机硬件和软件技术对数据进行有效的收集、存储、处理和应用的过程其目的在于充分有效地发挥数据的作用。 实现数据有效管理的关键是数据组织。 数据管理和数据治理的区别&am…...

Linux满载CPU和运行内存的方法
查询CPU详细信息命令如下: 查看物理CPU型号: cat /proc/cpuinfo | grep name | cut -f2 -d: | uniq -c查看物理CPU个数 cat /proc/cpuinfo| grep "physical id"| sort| uniq| wc -l查看每个物理CPU中core的个数(即核数) cat /proc/cpuinfo…...

每日五道java面试题之java基础篇(九)
目录: 第一题 你们项⽬如何排查JVM问题第二题 ⼀个对象从加载到JVM,再到被GC清除,都经历了什么过程?第三题 怎么确定⼀个对象到底是不是垃圾?第四题 JVM有哪些垃圾回收算法?第五题 什么是STW? 第…...

spring @Transactional注解参数详解
事物注解方式: Transactional 当标于类前时, 标示类中所有方法都进行事物处理 , 例子: 1 Transactional public class TestServiceBean implements TestService {}当类中某些方法不需要事物时: Transactional public class TestServiceBean implements TestService {private…...

D - 串结构练习——字符串连接
串结构练习——字符串连接 Description 给定两个字符串string1和string2,将字符串string2连接在string1的后面,并将连接后的字符串输出。 连接后字符串长度不超过110。 Input 输入包含多组数据,每组测试数据包含两行,第一行代表s…...

什么样的服务器是高性能服务器?
首先,高性能服务器应具备高处理能力。随着业务的不断扩展和数据量的爆炸性增长,高性能服务器需要具备强大的计算能力,能够快速处理各种复杂的业务和数据。这要求高性能服务器采用先进的处理器技术,如多核处理器、GPU加速等&#x…...

数学建模【线性规划】
一、线性规划简介 线性规划通俗讲就是“有限的资源中获取最大的收益”(优化类问题)。而且所有的变量关系式都是线性的,不存在x、指数函数、对数函数、反比例函数、三角函数等。此模型要优化的就是在一组线性约束条件下,求线性目标…...

ChatGPT的大致原理
国外有个博主写了一篇博文,名字叫TChatGPT: Explained to KidsQ」, 直译过来就是,给小孩子解释什么是ChatGPT。 因为现实是很多的小孩子已经可以用父母的手机版ChatGPT玩了 ,ChatGPT几乎可以算得上无所不知,起码给小孩…...
蓝桥杯备赛_python_BFS搜索算法_刷题学习笔记
1 bfs广度优先搜索 1.1 是什么 1.2怎么实现 2案例学习 2.1.走迷宫 2.2.P1443 马的遍历 2.3. 九宫重排(看答案学的,实在写不来) 2.4.青蛙跳杯子(学完九宫重排再做bingo) 2.5. 长草 3.总结 1 bfs广度优先搜索 【P…...

DockerHub与私有镜像仓库在容器化中的应用与管理
哈喽,大家好,我是左手python! Docker Hub的应用与管理 Docker Hub的基本概念与使用方法 Docker Hub是Docker官方提供的一个公共镜像仓库,用户可以在其中找到各种操作系统、软件和应用的镜像。开发者可以通过Docker Hub轻松获取所…...

镜像里切换为普通用户
如果你登录远程虚拟机默认就是 root 用户,但你不希望用 root 权限运行 ns-3(这是对的,ns3 工具会拒绝 root),你可以按以下方法创建一个 非 root 用户账号 并切换到它运行 ns-3。 一次性解决方案:创建非 roo…...

基于Docker Compose部署Java微服务项目
一. 创建根项目 根项目(父项目)主要用于依赖管理 一些需要注意的点: 打包方式需要为 pom<modules>里需要注册子模块不要引入maven的打包插件,否则打包时会出问题 <?xml version"1.0" encoding"UTF-8…...

IoT/HCIP实验-3/LiteOS操作系统内核实验(任务、内存、信号量、CMSIS..)
文章目录 概述HelloWorld 工程C/C配置编译器主配置Makefile脚本烧录器主配置运行结果程序调用栈 任务管理实验实验结果osal 系统适配层osal_task_create 其他实验实验源码内存管理实验互斥锁实验信号量实验 CMISIS接口实验还是得JlINKCMSIS 简介LiteOS->CMSIS任务间消息交互…...

多种风格导航菜单 HTML 实现(附源码)
下面我将为您展示 6 种不同风格的导航菜单实现,每种都包含完整 HTML、CSS 和 JavaScript 代码。 1. 简约水平导航栏 <!DOCTYPE html> <html lang"zh-CN"> <head><meta charset"UTF-8"><meta name"viewport&qu…...

【C++从零实现Json-Rpc框架】第六弹 —— 服务端模块划分
一、项目背景回顾 前五弹完成了Json-Rpc协议解析、请求处理、客户端调用等基础模块搭建。 本弹重点聚焦于服务端的模块划分与架构设计,提升代码结构的可维护性与扩展性。 二、服务端模块设计目标 高内聚低耦合:各模块职责清晰,便于独立开发…...

Unity | AmplifyShaderEditor插件基础(第七集:平面波动shader)
目录 一、👋🏻前言 二、😈sinx波动的基本原理 三、😈波动起来 1.sinx节点介绍 2.vertexPosition 3.集成Vector3 a.节点Append b.连起来 4.波动起来 a.波动的原理 b.时间节点 c.sinx的处理 四、🌊波动优化…...

回溯算法学习
一、电话号码的字母组合 import java.util.ArrayList; import java.util.List;import javax.management.loading.PrivateClassLoader;public class letterCombinations {private static final String[] KEYPAD {"", //0"", //1"abc", //2"…...

智能AI电话机器人系统的识别能力现状与发展水平
一、引言 随着人工智能技术的飞速发展,AI电话机器人系统已经从简单的自动应答工具演变为具备复杂交互能力的智能助手。这类系统结合了语音识别、自然语言处理、情感计算和机器学习等多项前沿技术,在客户服务、营销推广、信息查询等领域发挥着越来越重要…...

Golang——7、包与接口详解
包与接口详解 1、Golang包详解1.1、Golang中包的定义和介绍1.2、Golang包管理工具go mod1.3、Golang中自定义包1.4、Golang中使用第三包1.5、init函数 2、接口详解2.1、接口的定义2.2、空接口2.3、类型断言2.4、结构体值接收者和指针接收者实现接口的区别2.5、一个结构体实现多…...
