备战蓝桥杯---动态规划(入门3之子串问题)
本专题再介绍几种经典的字串问题。

这是一个两个不重叠字串和的问题,我们只要去枚举分界点c即可,我们不妨让c作为右区间的左边界,然后求[1,c)上的单个字串和并用max数组维护。对于右边,我们只要反向求单个字串和然后选左边界为c的一组即可。
下面是AC代码:
#include<stdio.h>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
long long t,a[50010],b[50010],max1[50010],n,ck[50010],hh;
int main(){scanf("%lld",&t);while(t--){memset(a,0,sizeof(a));memset(b,0,sizeof(b));memset(max1,0,sizeof(max1));scanf("%lld",&n);for(int i=1;i<=n;i++) scanf("%lld",&ck[i]);for(int i=1;i<=n;i++){if(i==1){a[i]=ck[i];max1[i]=ck[i];}else{a[i]=max(ck[i],ck[i]+a[i-1]);max1[i]=max(max1[i-1],a[i]);}}for(int i=n;i>=1;i--){if(i==n) b[i]=ck[i];else b[i]=max(ck[i],ck[i]+b[i+1]);}hh=-0x3f;for(int c=2;c<=n;c++){hh=max(hh,max1[c-1]+b[c]);}printf("%lld\n",hh);}
}接下来,我们加点难度:

现在2变成了m,我们进行升维操作,我们令f[i][j]为前j个数(第j个数必须取)组成的i个不相交子段最大和。
当我们要从j-->j+1时,对于第j+1,它可以作为最后一个子段的末尾,也可以不做末尾而是起点,而此时我们要去得到i-1个不相交子段的max,因此,我们易得转移方程为:
f[i][j]=max(f[i][j-1]+a[j],f[i-1][k]+a[j])
复杂度为o(n^2*m)
我们考虑优化一下:
f[i][j]=a[j]+max(f[i][j-1],f[i-1][k]).
我们只要维护每一个点对应的一列上从上到下的max即可。
至于初始条件,0组的情况都为0(就比如m=1,有一种情况就是只选他自己,因此要赋0)
下面是AC代码(dp数组用滚动即可):
#include<bits/stdc++.h>
using namespace std;
int n,m,a[1000100],mmm;
int ans,dp[1000100];
int ck[1000100];
int main(){while(scanf("%d%d",&m,&n)!=EOF){ans=-0x3f;for(int i=1;i<=n;i++) scanf("%d",&a[i]);memset(dp,0,sizeof(dp));memset(ck,0,sizeof(ck));for(int i=1;i<=m;i++){mmm=-0x3f;for(int j=i;j<=n;j++){dp[j]=max(dp[j-1],ck[j-1])+a[j];ck[j-1]=mmm;mmm=max(mmm,dp[j]);}}printf("%d\n",mmm); }
}让我们再加点难度:如果是环状呢?
有一道石子合并的通过复制一份来解决,但是因为这个不能利用上一次划分的情况,换句话说,这一次每次断开都要重新求(原因在于不是区间dp),于是我们不妨想一想另一种方法:
我们知道假如n与1没有被当成一段取,跟上面的就一样了。
如果n与1被当成一段取,那么我们在n与1断开的时候就相当于要求m+1段区间,其中第一段必须包含第一个元素,最后一个必须包含最后一个元素。
下面是AC代码(呜呜呜,直接初值赋了-0x3f,结果当成16进制,检查了好久):
#include<bits/stdc++.h>
using namespace std;
int n,m,a[200100],mmm,mmm1;
int ans,dp[200100],dp1[200100];
int ck[200100],ck1[200100],hou[200100],maxx[200100];
int main(){scanf("%d",&n);ck1[0]=-10000000;ans=-10000000;for(int i=1;i<=n;i++) scanf("%d",&a[i]);for(int i=1;i<=n;i++) dp1[i]=a[i]+dp1[i-1];for(int i=1;i<=n;i++) ck1[i]=max(dp1[i],ck1[i-1]);for(int i=n;i>=1;i--) hou[i]=a[i]+hou[i+1];for(int i=n;i>=1;i--){if(i==n) maxx[i]=a[i];else maxx[i]=max(maxx[i+1],hou[i]);}for(int i=1;i<=2;i++){mmm=-10000000;for(int j=i;j<=n;j++){dp[j]=max(dp[j-1],ck[j-1])+a[j];ck[j-1]=mmm;mmm=max(mmm,dp[j]);}}mmm1=-10000000;for(int j=2;j<=n;j++){dp1[j]=max(dp1[j-1],ck1[j-1])+a[j];ck1[j-1]=mmm1;mmm1=max(mmm1,dp1[j]);}for(int i=2;i<=n-1;i++){ans=max(ans,dp1[i]+maxx[i+1]);}printf("%d\n",max(mmm,ans)); }接下来,让我们再看看公共子序列问题吧:

我们以前也写过,我们把dp扩展成3维即可。
同时对于方案,我们一般用last数组记录上一次的情况,显然在这里就比较麻烦。我们可以用一个字符串,每次3个的最后一个元素相等时记录一下即可。
相关文章:

备战蓝桥杯---动态规划(入门3之子串问题)
本专题再介绍几种经典的字串问题。 这是一个两个不重叠字串和的问题,我们只要去枚举分界点c即可,我们不妨让c作为右区间的左边界,然后求[1,c)上的单个字串和并用max数组维护。对于右边,我们只要反向求单个字串和然后选左边界为c的…...

JavaScript:隐式类型转换与显式类型转换
文章目录 隐式类型转换(Implicit Type Conversion)1、字符串与数字的转换2、非布尔值到布尔值的转换3、在相等性比较中的转换4、对象到基础类型的转换5、在算术运算符中的其他转换 显式类型转换(Explicit Type Conversion)1、Numb…...

【电路笔记】-LR串联电路
LR串联电路 文章目录 LR串联电路1、概述2、示例1所有线圈、电感器、扼流圈和变压器都会在其周围产生磁场,由电感与电阻串联组成,形成 LR 串联电路。 1、概述 在本节有关电感器的第一个文章中,我们简要介绍了电感器的时间常数,指出流过电感器的电流不会瞬时变化,而是会以恒…...
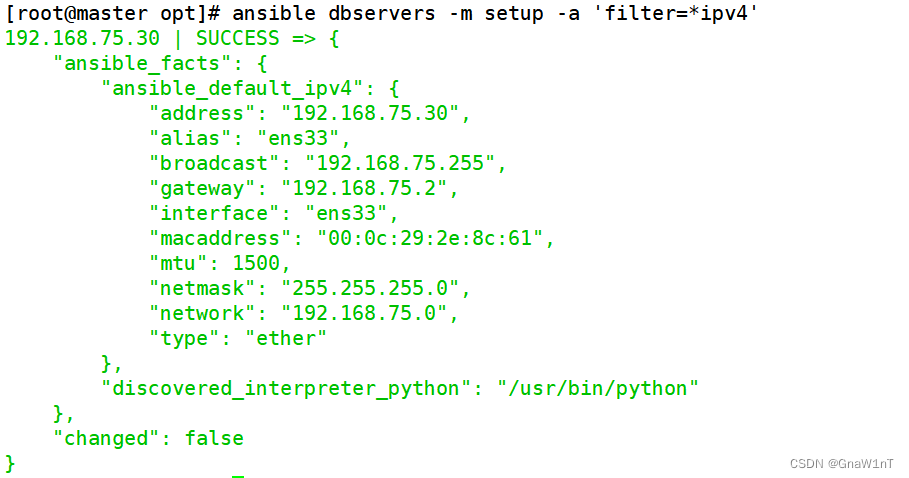
Ansible 自动化运维工具的使用
目录 Ansible的简介 ansible 环境安装部署 ansible 命令行模块 command 模块 shell 模块 cron 模块 user 模块 group 模块 copy 模块 file 模块 hostname 模块 ping 模块 yum 模块 service/systemd 模块 script 模块 mount 模块 archive 模块 unarchive 模…...

亚马逊、ozon、速卖通、Lazada等跨境平台为什么评论老是被删
对于卖家而言,最难的并不是销售量,最难的是让客户在购买后能够留下一个高质量的review,毕竟现在的市场,以listing的排名为基准,以review数量多少和质量的高低来评判店铺的好坏 几乎所有的卖家都会有索评的烦恼&#x…...

手把手带你在Linux上安装带GPU加速的opencv库(C++版本)
1.安装依赖 sudo apt-get install build-essential cmake git libgtk2.0-dev pkg-config libavcodec-dev libavformat-dev libswscale-dev sudo apt-get install python-dev python-numpy python3-dev python3-numpy sudo apt-get install libtbb2 libtbb-dev libjpeg-dev l…...

【Linux】软件包管理器 yum | vim编辑器
前言: 软件包管理器 yum和vim编辑器讲解 文章目录 软件包管理器 yum编辑器-vim四种模式普通模式批量化注释和批量化去注释末行模式临时文件 软件包管理器 yum yum(Yellowdog Updater, Modified)是一个在基于 RPM(管理软件包的格式和工具集合&…...

vue常见问题
文章目录 data为什么是一个函数,而不是一个对象?什么情况下可以使用对象?key的作用,为什么不能用Index?render函数,h函数,和template什么关系?vue 是怎么解析template的? template会…...
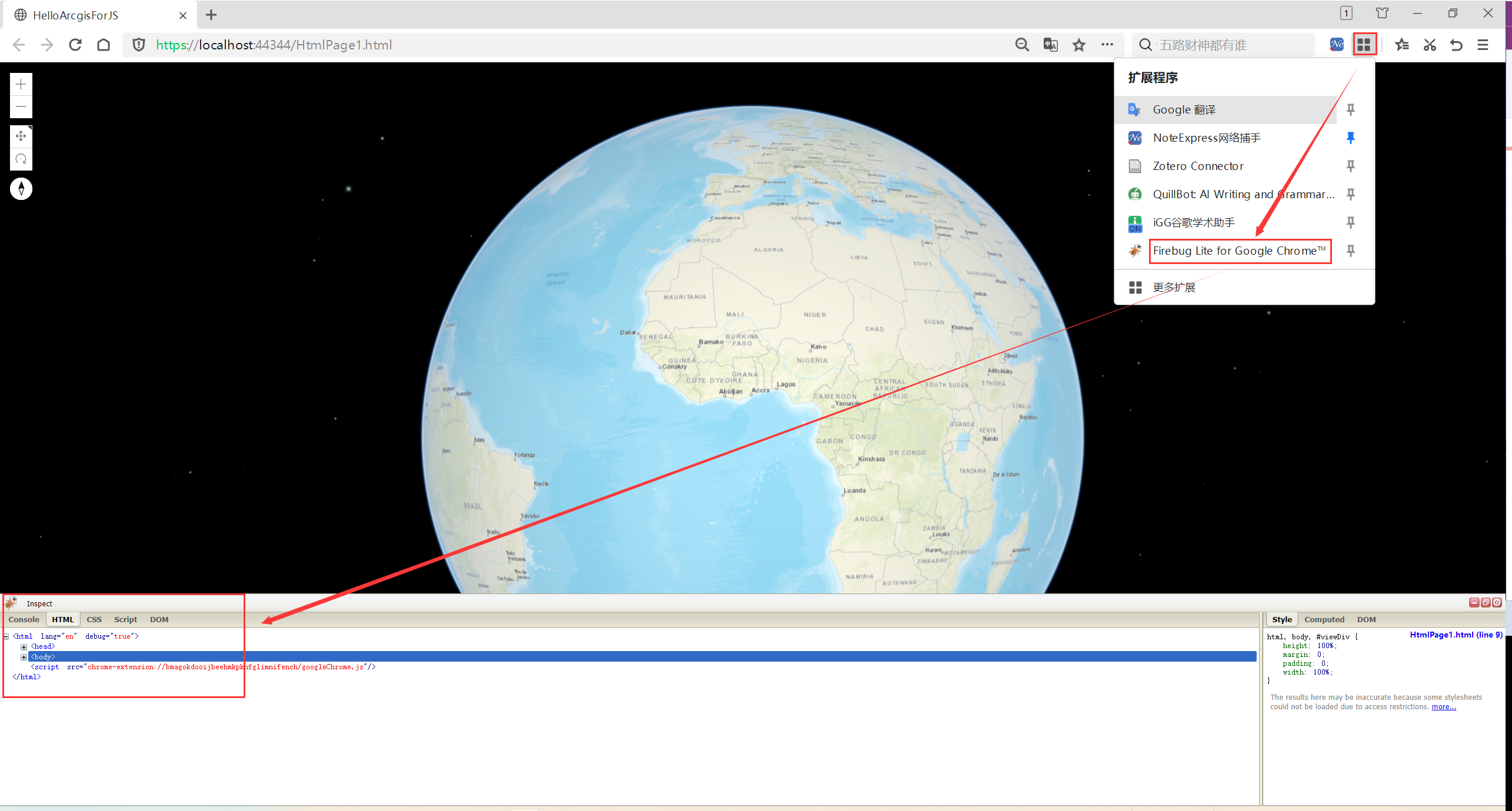
ArcgisForJS基础
文章目录 0.引言1.第一个ArcgisForJS应用程序1.1.安装部署ArcgisForJS1.2.实现ArcgisForJS应用程序 2.开发与调试工具2.1.集成开发环境2.2.调试工具2.3.Firebug 0.引言 ArcGIS API for JavaScript是一款由Esri公司开发的用于创建WebGIS应用的JavaScript库。它允许开发者通过调…...
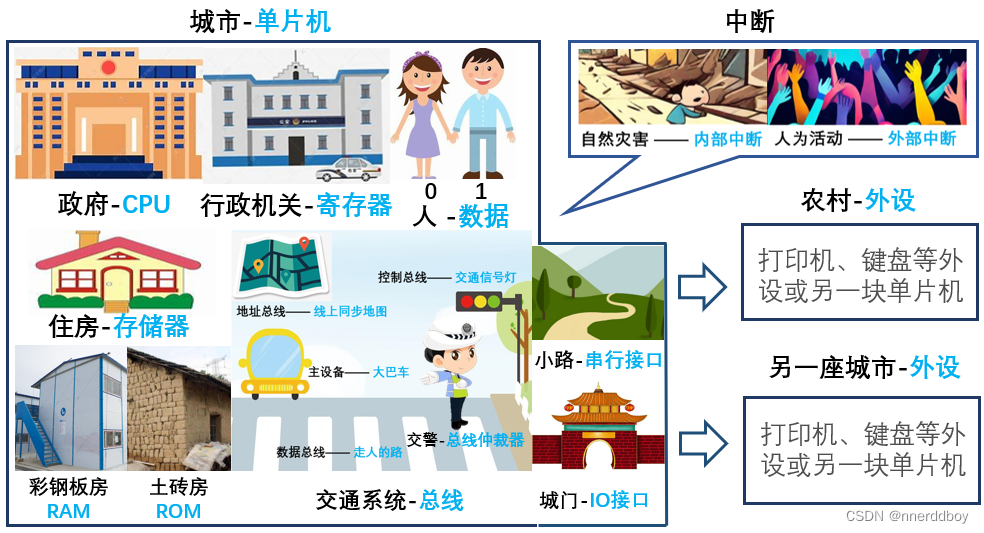
白话微机:5.解释串行接口以及一些考研面试问题
一. 前言(回顾世界观) 很久很久以前,有这样一个世界,这个世界有着现实世界一样的元素:那里的人又有一个别的名字叫做“数据”,人有0有1;人们也有住房,这些住房在这个世界叫做“存储器…...

版本控制(Git)
Fork 本课程网站的仓库 将版本历史可视化并进行探索是谁最后修改了 README.md文件?(提示:使用 git log 命令并添加合适的参数)最后一次修改_config.yml 文件中 collections: 行时的提交信息是什么?(提示&am…...

USB-C音频转接器:实现边充电边听歌的新选择 | LDR6020P
随着科技浪潮的推进,Type-C接口已逐渐成为电子设备的主流选择,以其正反随意插、高速传输和强大功能等独特优势,在日常生活中占据越来越重要的地位。而Type-C音频转接器,作为连接Type-C接口与音频设备的桥梁,正引领着音…...

C/C++ 怎么把多个静态库给整合成一个静态库?
来源:https://www.wikitechy.com/tutorials/linux/how-to-merge-two-ar-static-libraries-into-one 使用 libtool (这也是可移植性最强的方式)(但这通常要求两个子库也是 libtool 制作的) libtool --modelink cc -static -o libaz.la libab…...

OBD部署OceanBase集群-配置文件方式
前一篇文章介绍了OBD白屏可视化方式部署OceanBase集群 ,其原理是把可视化设置生成为一个配置文件,然后使用OBD命令部署集群 本篇想使用命令行加配置文件方式,只部署OceanBase和ODProxy两个组件 服务器参数配置和 oceanbase-all-in-one-*.ta…...
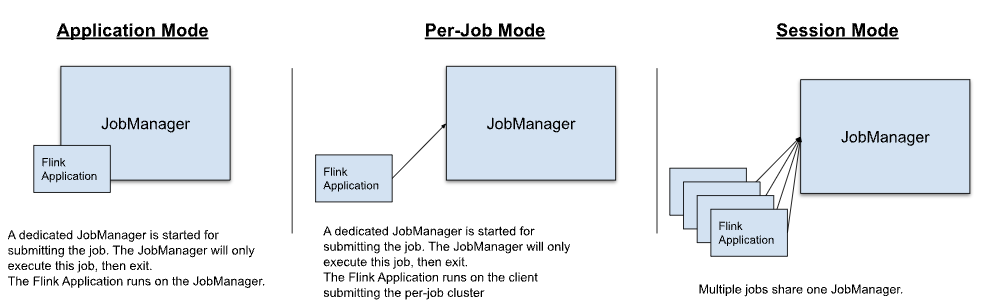
Flink介绍
Flink 介绍 文章目录 Flink 介绍1. 简介1.1 背景1.2 用途 2. 核心概念2.1 流(Stream)2.2 转换(Transformation)2.3 窗口(Window)2.4 状态(State) 3. 编程模型3.1 编程模型介绍3.2 程…...
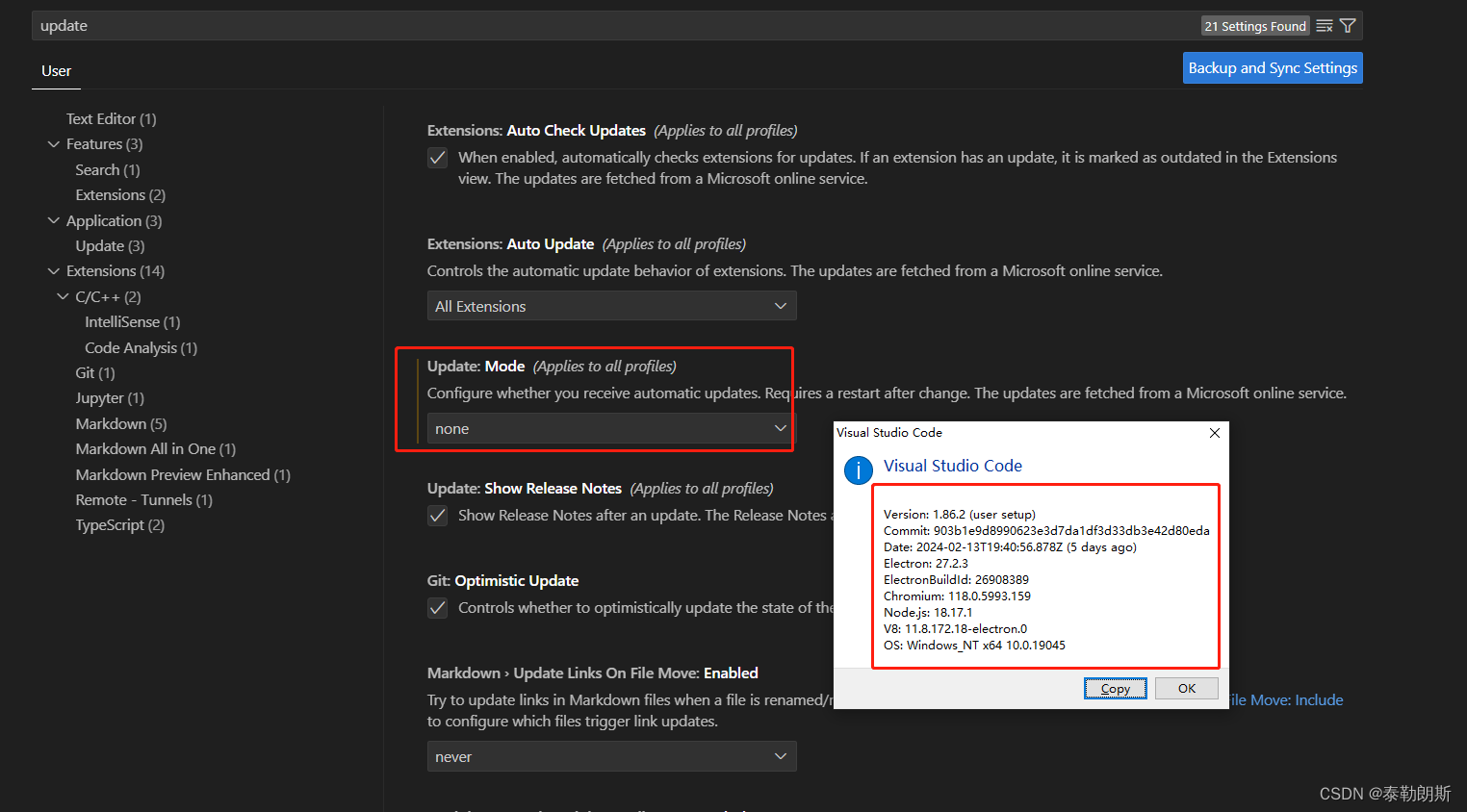
vscode突然连不上服务器了,以前都可以的,并且ssh等其它方式是可以连接到服务器的
过完年回来准备开工干活,突然发现vscode连不上服务器了,奇了怪了,年前都可以的,看了一下报错,如下, 以为是服务器挂了,结果执行ssh xxxxxx 发现是可以远程连接的,看来服务器没有问题…...

【shell】Shell学习后篇
Linux 常用 Shell 文章目录 Linux 常用 ShellBanner设置字体颜色设置提示操作系统操作系统版本号系统处理器架构关闭防火墙和SELinux系统操作防火墙相关获取当前目录判断文件是否存在判断目录是否存在后台挂起静默执行判断之前的命令是否成功 Banner 设置字体颜色 RED\033[31…...

协同程序原理
一、协程的本质 //协程可以分为两个部分 //1.协程函数本体 //2.协程调度器 //协程本体就是一个能够中间暂停返回的函数 //协程调度器是Unity内部实现的,会在对应的时机帮我们继续执行协程函数 //Unity只实现了协程调度器部分 //协程的本体本质上就是 C#的一个迭代…...

怎样保证数据库和redis里的数据一致性
使用缓存更新策略:在更新数据库时,同时更新Redis中相应的数据。这可以通过编写代码来实现,在数据库更新操作完成后,同步更新Redis中对应的数据。这可以通过在代码中使用事务来保证更新的原子性,确保数据库和Redis中的数…...
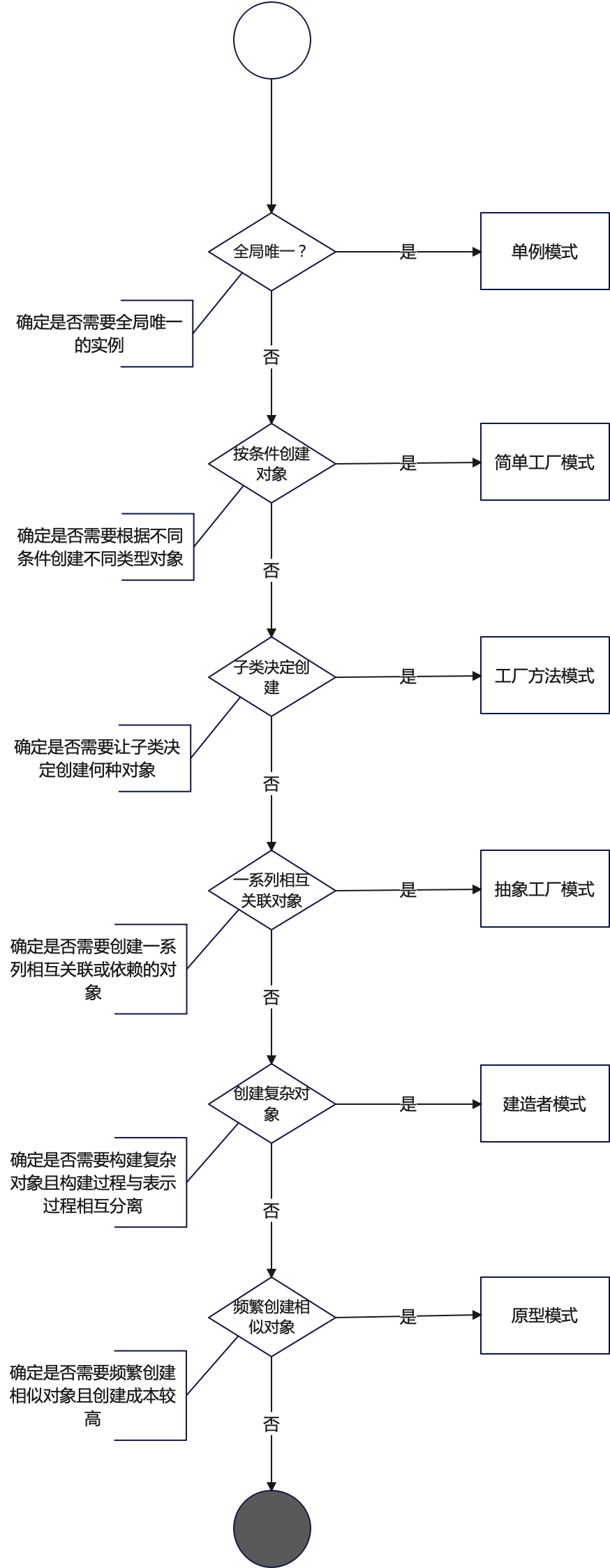
探索设计模式的魅力:创建型设计模式的比较与决策
设计模式专栏:http://t.csdnimg.cn/U54zu 目录 一、设计模式概览 1.1 创建型模式 二、比较创建型设计模式 1.1 适用场景典型用例 1.2 关键要素与差异对比 1.3 结构图 三、模式选择指南 3.1 场景分析 3.2 决策流程图 四、结语 4.1 优势 4.2 考量因素 一、…...

使用VSCode开发Django指南
使用VSCode开发Django指南 一、概述 Django 是一个高级 Python 框架,专为快速、安全和可扩展的 Web 开发而设计。Django 包含对 URL 路由、页面模板和数据处理的丰富支持。 本文将创建一个简单的 Django 应用,其中包含三个使用通用基本模板的页面。在此…...

Flask RESTful 示例
目录 1. 环境准备2. 安装依赖3. 修改main.py4. 运行应用5. API使用示例获取所有任务获取单个任务创建新任务更新任务删除任务 中文乱码问题: 下面创建一个简单的Flask RESTful API示例。首先,我们需要创建环境,安装必要的依赖,然后…...

<6>-MySQL表的增删查改
目录 一,create(创建表) 二,retrieve(查询表) 1,select列 2,where条件 三,update(更新表) 四,delete(删除表…...

【算法训练营Day07】字符串part1
文章目录 反转字符串反转字符串II替换数字 反转字符串 题目链接:344. 反转字符串 双指针法,两个指针的元素直接调转即可 class Solution {public void reverseString(char[] s) {int head 0;int end s.length - 1;while(head < end) {char temp …...

优选算法第十二讲:队列 + 宽搜 优先级队列
优选算法第十二讲:队列 宽搜 && 优先级队列 1.N叉树的层序遍历2.二叉树的锯齿型层序遍历3.二叉树最大宽度4.在每个树行中找最大值5.优先级队列 -- 最后一块石头的重量6.数据流中的第K大元素7.前K个高频单词8.数据流的中位数 1.N叉树的层序遍历 2.二叉树的锯…...
)
Android第十三次面试总结(四大 组件基础)
Activity生命周期和四大启动模式详解 一、Activity 生命周期 Activity 的生命周期由一系列回调方法组成,用于管理其创建、可见性、焦点和销毁过程。以下是核心方法及其调用时机: onCreate() 调用时机:Activity 首次创建时调用。…...
多光源(Multiple Lights))
C++.OpenGL (14/64)多光源(Multiple Lights)
多光源(Multiple Lights) 多光源渲染技术概览 #mermaid-svg-3L5e5gGn76TNh7Lq {font-family:"trebuchet ms",verdana,arial,sans-serif;font-size:16px;fill:#333;}#mermaid-svg-3L5e5gGn76TNh7Lq .error-icon{fill:#552222;}#mermaid-svg-3L5e5gGn76TNh7Lq .erro…...

深度剖析 DeepSeek 开源模型部署与应用:策略、权衡与未来走向
在人工智能技术呈指数级发展的当下,大模型已然成为推动各行业变革的核心驱动力。DeepSeek 开源模型以其卓越的性能和灵活的开源特性,吸引了众多企业与开发者的目光。如何高效且合理地部署与运用 DeepSeek 模型,成为释放其巨大潜力的关键所在&…...

智能职业发展系统:AI驱动的职业规划平台技术解析
智能职业发展系统:AI驱动的职业规划平台技术解析 引言:数字时代的职业革命 在当今瞬息万变的就业市场中,传统的职业规划方法已无法满足个人和企业的需求。据统计,全球每年有超过2亿人面临职业转型困境,而企业也因此遭…...

npm安装electron下载太慢,导致报错
npm安装electron下载太慢,导致报错 背景 想学习electron框架做个桌面应用,卡在了安装依赖(无语了)。。。一开始以为node版本或者npm版本太低问题,调整版本后还是报错。偶尔执行install命令后,可以开始下载…...
