曲线生成 | 图解B样条曲线生成原理(基本概念与节点生成算法)
目录
- 0 专栏介绍
- 1 什么是B样条曲线?
- 2 基函数的de Boor递推式
- 3 B样条曲线基本概念图解
- 4 节点生成公式
0 专栏介绍
🔥附C++/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等);局部规划(DWA、APF等);曲线优化(贝塞尔曲线、B样条曲线等)。
🚀详情:图解自动驾驶中的运动规划(Motion Planning),附几十种规划算法
1 什么是B样条曲线?
为了解决贝塞尔曲线无法局部修正、控制性减弱、曲线次数过高、不易拼接的缺陷,引入B样条曲线(B-Spline)。对贝塞尔曲线不了解的同学请看曲线生成 | 图解贝塞尔曲线生成原理(附ROS C++/Python/Matlab仿真)
B样条曲线是一种用于表示和描绘曲线的数学工具,它在计算机图形学、计算机辅助设计、计算机动画和数值分析等领域得到广泛应用。其名称中的B代表了基本(basis),而样条则是在各个领域中广泛应用的一种绘制曲线的技术,例如计算机图形学、物理学模拟、金融和经济分析等。在计算机图形学中,样条通常用于创建平滑的曲线和曲面,以便在三维场景中呈现出更真实的效果。在物理学模拟中,样条可用于描述物体的运动轨迹和变形过程。

B样条曲线的性质包括平滑性、局部控制性、递归计算和多项式插值。通过调整控制点的位置、权重和节点序列,可以改变B样条曲线的形状,从而实现对曲线的精确控制。B样条曲线常用于描述自然曲线和复杂曲线,如汽车外形、飞机机翼、艺术造型等。在计算机图形学中,B样条曲线可以用来生成圆滑的曲线路径,进行形状建模和渲染,以及实现动画效果等。
在运动规划中,B样条曲线也是一种很强大的曲线生成和轨迹优化工具,接下来介绍其基本原理。
2 基函数的de Boor递推式
B样条曲线的核心是具有局部性的基函数(Basic function)——当改变一个控制节点时,只会变动该点旁边有限段曲线(样条曲线则需要重新计算整条曲线,因为它由一组控制点唯一确定),而非“牵一发动全身”。如图所示给出了B样条与贝塞尔曲线基函数的区别。

采用Cox-de Boor递推定义B样条曲线的基函数
N i , k ( t ) = t − t i t i + k − t i N i , k − 1 ( t ) + t i + k + 1 − t t i + k + 1 − t i + 1 N i + 1 , k − 1 ( t ) N_{i,k}\left( t \right) =\frac{t-t_i}{t_{i+k}-t_i}N_{i,k-1}\left( t \right) +\frac{t_{i+k+1}-t}{t_{i+k+1}-t_{i+1}}N_{i+1,k-1}\left( t \right) Ni,k(t)=ti+k−tit−tiNi,k−1(t)+ti+k+1−ti+1ti+k+1−tNi+1,k−1(t)
其中 N i , k ( t ) N_{i,k}\left( t \right) Ni,k(t)称为第 i i i个控制节点的 k k k次( k + 1 k+1 k+1阶)B样条基函数, i = 0 , 1 , ⋯ , n − 1 i=0,1,\cdots ,n-1 i=0,1,⋯,n−1, k ⩾ 1 k\geqslant 1 k⩾1且规定 0 / 0 = 0 {{0}/{0}}=0 0/0=0。特别地,有
N i , 0 ( t ) = { 1 , t ∈ [ t i , t i + 1 ) 0 , o t h e r w i s e N_{i,0}\left( t \right) =\begin{cases} 1,t\in \left[ t_i,t_{i+1} \right)\\ 0,\mathrm{otherwise}\\\end{cases} Ni,0(t)={1,t∈[ti,ti+1)0,otherwise
即高次B样条基函数为若干低次B样条基函数的线性组合。 N i , k ( t ) N_{i,k}\left( t \right) Ni,k(t)的次数 k k k与控制节点的个数 n n n无关,因此B样条曲线自由度更大——允许定义多个控制点而不用担心曲线次数过高导致计算困难。
3 B样条曲线基本概念图解
B样条曲线定义为用基函数加权的控制节点
P ( t ) = ∑ i = 0 n − 1 p i N i , k ( t ) , t ∈ [ t k , t n ) \boldsymbol{P}\left( t \right) =\sum_{i=0}^{n-1}{\boldsymbol{p}_iN_{i,k}\left( t \right)}, t\in \left[ t_k,t_n \right) P(t)=i=0∑n−1piNi,k(t),t∈[tk,tn)
其中 T = { t 0 , t 1 , ⋯ , t m − 1 } T=\left\{ t_0,t_1,\cdots ,t_{m-1} \right\} T={t0,t1,⋯,tm−1}是一个一维单调非递减序列,称为节点向量(knot vector),其中的元素 t i t_i ti称为节点(knot),区间 [ t i , t i + 1 ) \left[ t_i,t_{i+1} \right) [ti,ti+1)称为第 i i i个节点区间(knot range),节点在样条曲线上的映射 P ( t i ) \boldsymbol{P}\left( t_i \right) P(ti)称为曲节点(knot point)。
在节点向量中,若某节点 t i t_i ti出现 l l l次,则称 t i t_i ti是重复度为 l l l的多重节点,否则为简单节点。与贝塞尔曲线不同,仅当B样条曲线首末节点重复度为 k + 1 k+1 k+1时,曲线本身才穿过首末控制点。
接下来分析B样条曲线的局部支撑性。基函数 N i , k ( t ) N_{i,k}\left( t \right) Ni,k(t)在区间 [ t i , t i + k + 1 ] \left[ t_i,t_{i+k+1} \right] [ti,ti+k+1]上非零,因为该区间上总存在不为零的零阶基函数 N i , 0 N_{i,0} Ni,0,该区间称为支撑区间,对应样条曲线上的区段称为支撑曲线。由于 N i , k ( t ) N_{i,k}\left( t \right) Ni,k(t)直接与控制节点 p i \boldsymbol{p}_i pi相乘,所以 p i \boldsymbol{p}_i pi只影响其支撑区间 [ t i , t i + k + 1 ] \left[ t_i,t_{i+k+1} \right] [ti,ti+k+1]上对应支撑曲线的形状。所以B样条曲线也可视为若干段贝塞尔曲线的拼接,是贝塞尔曲线的推广,相邻贝塞尔曲线间存在若干重合节点,保留了对称性、几何不变性、变差伸缩性等优良特性。

为使每个控制节点都有合法的支撑区间与之匹配,节点数量应满足
m = n + k + 1 m=n+k+1 m=n+k+1
B样条曲线的次数指基函数多项式的最高次数,阶数则可视为控制节点 p i \boldsymbol{p}_i pi所影响的节点数。当节点区间 [ t i , t i + 1 ) \left[ t_i,t_{i+1} \right) [ti,ti+1)上的非零 k k k次基函数达到最大数量 k + 1 k+1 k+1个时,令其满足
∑ j = i − k i N j , k = 1 \sum_{j=i-k}^i{N_{j,k}}=1 j=i−k∑iNj,k=1
称为基函数的加权性质。显然,对于 k k k次基函数,节点区间 [ t 0 , t k ) \left[ t_0,t_k \right) [t0,tk)与 [ t n , t n + k ) \left[ t_n,t_{n+k} \right) [tn,tn+k)上的非零基函数不足 k + 1 k+1 k+1个,它们的加权和不为零,在这些区间计算B样条曲线会导致错误,因此B样条曲线定义在区间 [ t k , t n ) \left[ t_k,t_n \right) [tk,tn)上。如图所示是关于B样条曲线定义区间的实例说明。

4 节点生成公式
B样条曲线由控制节点与节点向量唯一确定,通过改变节点向量中节点的分布特征,可以构造不同类型的B样条曲线
-
均匀B样条曲线(Uniform B-Spline Curve)
节点向量中的节点沿数轴方向等距离均匀分布,所有节点区间等距,即 t i + 1 − t i = c o n s t > 0 , i = 0 , 1 , ⋯ , n + k t_{i+1}-t_i=\mathrm{const}>0, i=0,1,\cdots ,n+k ti+1−ti=const>0,i=0,1,⋯,n+k
-
准均匀B样条曲线(quasi-Uniform B-Spline Curve)
节点向量中的首末节点重复度为 k + 1 k+1 k+1,其余节点沿数轴方向等距均匀分布且重复度为1。可以证明该情况下,当 k = n k=n k=n时,B样条基函数 N i , k ( t ) N_{i,k}\left( t \right) Ni,k(t)退化为伯恩斯坦多项式,即B样条曲线退化为贝塞尔曲线。
-
非均匀B样条曲线(non-Uniform B-Spline Curve)
节点向量任意分布
节点生成通常有两种方法:
- 均匀法
{ t 0 = t 1 = ⋯ = t k = 0 t k + i = i n − k + 1 , i = 1 , 2 , ⋯ , n − k − 1 t n = t n + 1 = ⋯ = t n + k = 1 \begin{cases} t_0=t_1=\cdots =t_k=0\\ t_{k+i}=\frac{i}{n-k+1}, i=1,2,\cdots ,n-k-1\\ t_n=t_{n+1}=\cdots =t_{n+k}=1\\\end{cases} ⎩ ⎨ ⎧t0=t1=⋯=tk=0tk+i=n−k+1i,i=1,2,⋯,n−k−1tn=tn+1=⋯=tn+k=1
该方法不依赖于参数选择。 - De Boor法
{ t 0 = t 1 = ⋯ = t k = 0 t k + i = 1 k ∑ j = i i + k − 1 u j , i = 1 , 2 , ⋯ , n − k − 1 t n = t n + 1 = ⋯ = t n + k = 1 \begin{cases} t_0=t_1=\cdots =t_k=0\\ t_{k+i}=\frac{1}{k}\sum_{j=i}^{i+k-1}{u_j}, i=1,2,\cdots ,n-k-1\\ t_n=t_{n+1}=\cdots =t_{n+k}=1\\\end{cases} ⎩ ⎨ ⎧t0=t1=⋯=tk=0tk+i=k1∑j=ii+k−1uj,i=1,2,⋯,n−k−1tn=tn+1=⋯=tn+k=1
该方法对选择的参数进行窗口平滑。
下一节将继续介绍B样条曲线的计算算法——近似和插值应用,并给出代码实现。
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …
相关文章:

曲线生成 | 图解B样条曲线生成原理(基本概念与节点生成算法)
目录 0 专栏介绍1 什么是B样条曲线?2 基函数的de Boor递推式3 B样条曲线基本概念图解4 节点生成公式 0 专栏介绍 🔥附C/Python/Matlab全套代码🔥课程设计、毕业设计、创新竞赛必备!详细介绍全局规划(图搜索、采样法、智能算法等)…...

CyberDAO:web3时代的引领者
Web3.0正在改写着世界运行的规则,AGI将为人类未来的生产效率、工作方式与目标带来改变,区块链经过十余年发展开启了去中心化新格局,带来生产关系的变革。人类正在从过往以时间换取收入、听命完成工作,转变为以个性化、自主追求人生…...
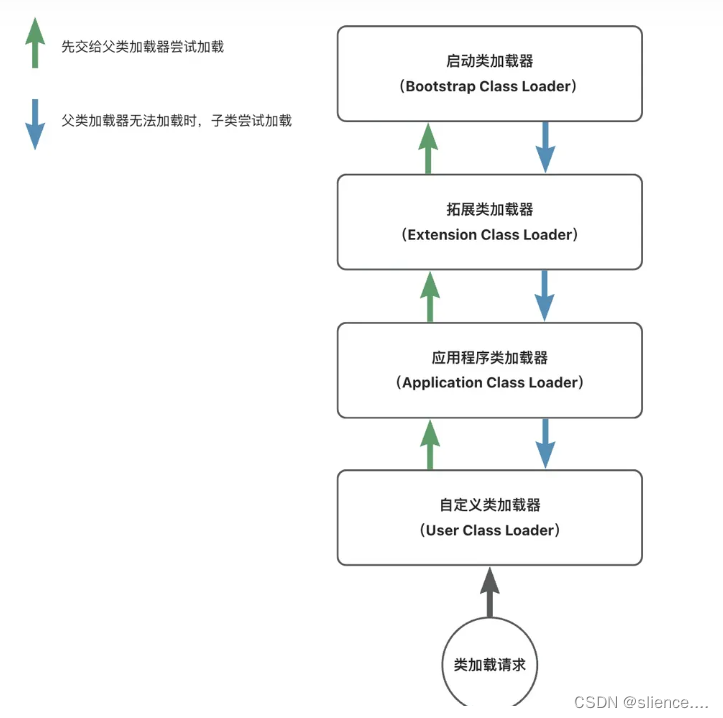
java以及android类加载机制
类加载机制 一、Java类加载机制 java中,每一个类或者接口,在编译后,都会生成一个.class文件。 类加载机制指的是将这些.class文件中的二进制数据读入到内存中并对数据进行校验,解析和初始化。最终,每一个类都会在方…...

【Go】四、rpc跨语言编程基础与rpc的调用基础原理
Go管理工具 早期 Go 语言不使用 go module 进行包管理,而是使用 go path 进行包管理,这种管理方式十分老旧,两者最显著的区别就是:Go Path 创建之后没有 go.mod 文件被创建出来,而 go module 模式会创建出一个 go.mod…...

Linux CentOS系统安装SQL Server并结合内网穿透实现公网访问本地数据
🔥博客主页: 小羊失眠啦. 🎥系列专栏:《C语言》 《数据结构》 《C》 《Linux》 《Cpolar》 ❤️感谢大家点赞👍收藏⭐评论✍️ 前些天发现了一个巨牛的人工智能学习网站,通俗易懂,风趣幽默&…...
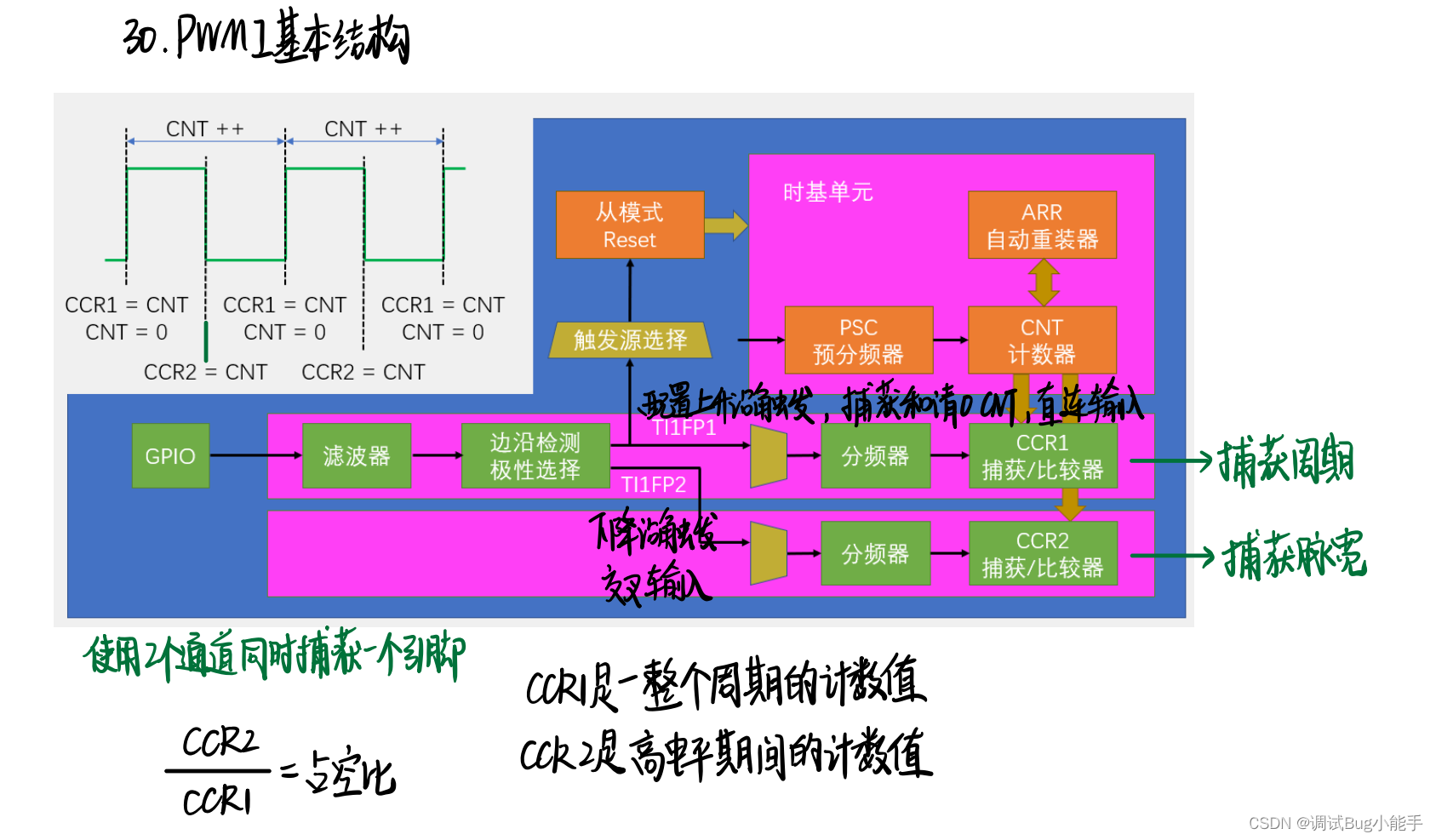
输入捕获模式测频率PWM输入模式(PWMI)测占空比
一、概念介绍 输出比较: 比较电路输入的CNT、CCR大小关系 ,在通道引脚输出高低电平 二、*频率知识、测量方法补充 * N/fc得到标准频率的时长,也就是待测频率的周期 测频法代码实现:修改对射式红外传感器计次(上升沿…...

解锁VIP会员漫画:用Python爬虫轻松实现高清漫画下载
嗨喽~大家好呀,这里是魔王呐 ❤ ~! python更多源码/资料/解答/教程等 点击此处跳转文末名片免费获取 环境使用: Python 3.10 Pycharm 模块使用: requests >>> pip install requests 数据请求模块 parsel >>> pip install parsel 数据解析模块…...

备战蓝桥杯---动态规划(入门3之子串问题)
本专题再介绍几种经典的字串问题。 这是一个两个不重叠字串和的问题,我们只要去枚举分界点c即可,我们不妨让c作为右区间的左边界,然后求[1,c)上的单个字串和并用max数组维护。对于右边,我们只要反向求单个字串和然后选左边界为c的…...

JavaScript:隐式类型转换与显式类型转换
文章目录 隐式类型转换(Implicit Type Conversion)1、字符串与数字的转换2、非布尔值到布尔值的转换3、在相等性比较中的转换4、对象到基础类型的转换5、在算术运算符中的其他转换 显式类型转换(Explicit Type Conversion)1、Numb…...

【电路笔记】-LR串联电路
LR串联电路 文章目录 LR串联电路1、概述2、示例1所有线圈、电感器、扼流圈和变压器都会在其周围产生磁场,由电感与电阻串联组成,形成 LR 串联电路。 1、概述 在本节有关电感器的第一个文章中,我们简要介绍了电感器的时间常数,指出流过电感器的电流不会瞬时变化,而是会以恒…...
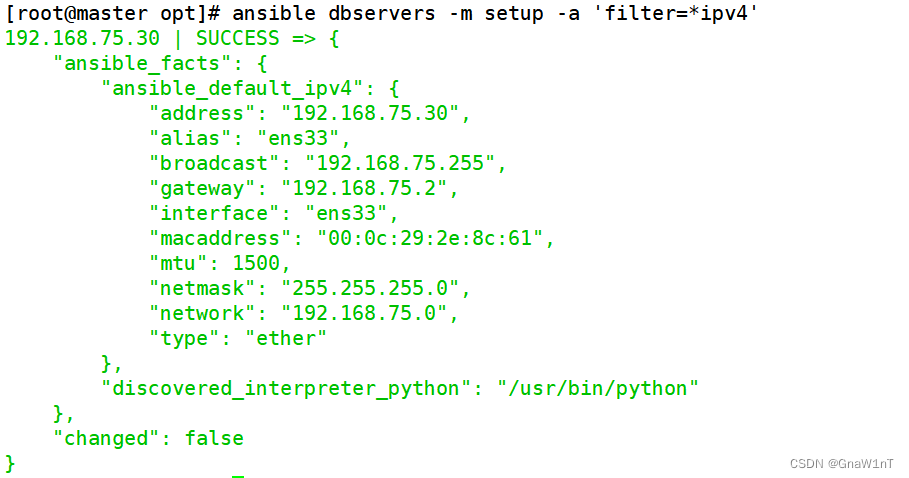
Ansible 自动化运维工具的使用
目录 Ansible的简介 ansible 环境安装部署 ansible 命令行模块 command 模块 shell 模块 cron 模块 user 模块 group 模块 copy 模块 file 模块 hostname 模块 ping 模块 yum 模块 service/systemd 模块 script 模块 mount 模块 archive 模块 unarchive 模…...

亚马逊、ozon、速卖通、Lazada等跨境平台为什么评论老是被删
对于卖家而言,最难的并不是销售量,最难的是让客户在购买后能够留下一个高质量的review,毕竟现在的市场,以listing的排名为基准,以review数量多少和质量的高低来评判店铺的好坏 几乎所有的卖家都会有索评的烦恼&#x…...

手把手带你在Linux上安装带GPU加速的opencv库(C++版本)
1.安装依赖 sudo apt-get install build-essential cmake git libgtk2.0-dev pkg-config libavcodec-dev libavformat-dev libswscale-dev sudo apt-get install python-dev python-numpy python3-dev python3-numpy sudo apt-get install libtbb2 libtbb-dev libjpeg-dev l…...

【Linux】软件包管理器 yum | vim编辑器
前言: 软件包管理器 yum和vim编辑器讲解 文章目录 软件包管理器 yum编辑器-vim四种模式普通模式批量化注释和批量化去注释末行模式临时文件 软件包管理器 yum yum(Yellowdog Updater, Modified)是一个在基于 RPM(管理软件包的格式和工具集合&…...

vue常见问题
文章目录 data为什么是一个函数,而不是一个对象?什么情况下可以使用对象?key的作用,为什么不能用Index?render函数,h函数,和template什么关系?vue 是怎么解析template的? template会…...
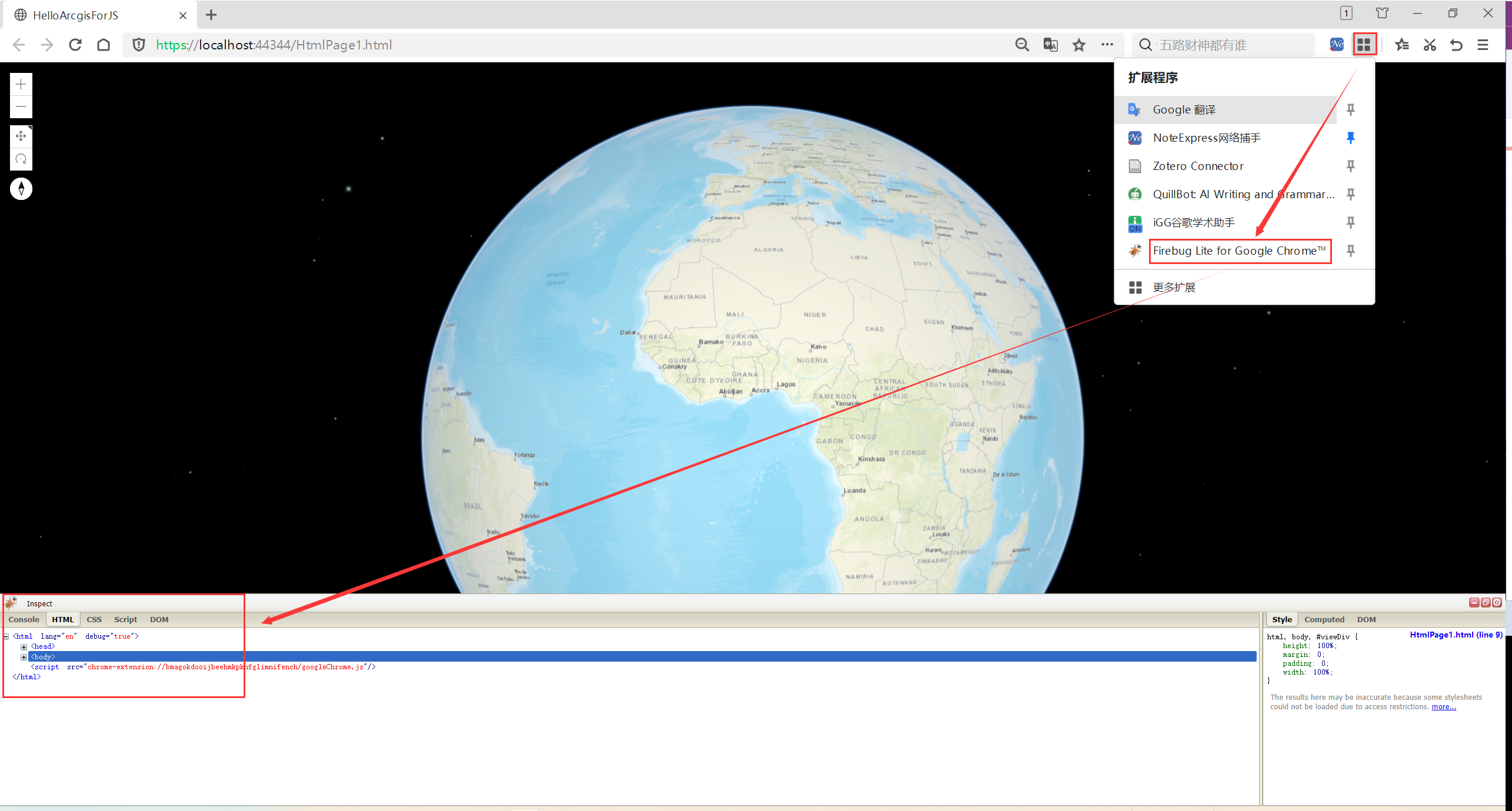
ArcgisForJS基础
文章目录 0.引言1.第一个ArcgisForJS应用程序1.1.安装部署ArcgisForJS1.2.实现ArcgisForJS应用程序 2.开发与调试工具2.1.集成开发环境2.2.调试工具2.3.Firebug 0.引言 ArcGIS API for JavaScript是一款由Esri公司开发的用于创建WebGIS应用的JavaScript库。它允许开发者通过调…...
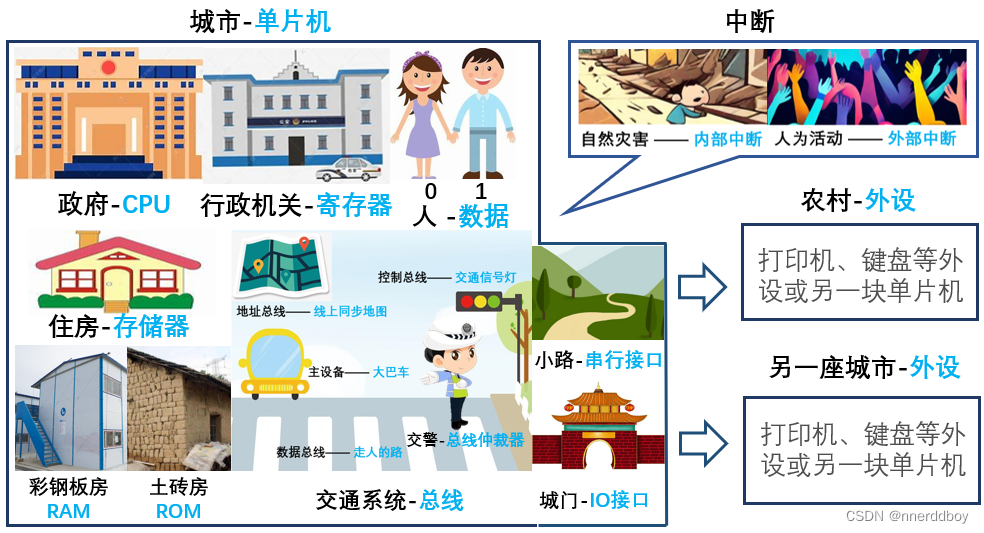
白话微机:5.解释串行接口以及一些考研面试问题
一. 前言(回顾世界观) 很久很久以前,有这样一个世界,这个世界有着现实世界一样的元素:那里的人又有一个别的名字叫做“数据”,人有0有1;人们也有住房,这些住房在这个世界叫做“存储器…...

版本控制(Git)
Fork 本课程网站的仓库 将版本历史可视化并进行探索是谁最后修改了 README.md文件?(提示:使用 git log 命令并添加合适的参数)最后一次修改_config.yml 文件中 collections: 行时的提交信息是什么?(提示&am…...

USB-C音频转接器:实现边充电边听歌的新选择 | LDR6020P
随着科技浪潮的推进,Type-C接口已逐渐成为电子设备的主流选择,以其正反随意插、高速传输和强大功能等独特优势,在日常生活中占据越来越重要的地位。而Type-C音频转接器,作为连接Type-C接口与音频设备的桥梁,正引领着音…...

C/C++ 怎么把多个静态库给整合成一个静态库?
来源:https://www.wikitechy.com/tutorials/linux/how-to-merge-two-ar-static-libraries-into-one 使用 libtool (这也是可移植性最强的方式)(但这通常要求两个子库也是 libtool 制作的) libtool --modelink cc -static -o libaz.la libab…...

【SpringBoot】100、SpringBoot中使用自定义注解+AOP实现参数自动解密
在实际项目中,用户注册、登录、修改密码等操作,都涉及到参数传输安全问题。所以我们需要在前端对账户、密码等敏感信息加密传输,在后端接收到数据后能自动解密。 1、引入依赖 <dependency><groupId>org.springframework.boot</groupId><artifactId...

关于iview组件中使用 table , 绑定序号分页后序号从1开始的解决方案
问题描述:iview使用table 中type: "index",分页之后 ,索引还是从1开始,试过绑定后台返回数据的id, 这种方法可行,就是后台返回数据的每个页面id都不完全是按照从1开始的升序,因此百度了下,找到了…...

STM32标准库-DMA直接存储器存取
文章目录 一、DMA1.1简介1.2存储器映像1.3DMA框图1.4DMA基本结构1.5DMA请求1.6数据宽度与对齐1.7数据转运DMA1.8ADC扫描模式DMA 二、数据转运DMA2.1接线图2.2代码2.3相关API 一、DMA 1.1简介 DMA(Direct Memory Access)直接存储器存取 DMA可以提供外设…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

在Ubuntu24上采用Wine打开SourceInsight
1. 安装wine sudo apt install wine 2. 安装32位库支持,SourceInsight是32位程序 sudo dpkg --add-architecture i386 sudo apt update sudo apt install wine32:i386 3. 验证安装 wine --version 4. 安装必要的字体和库(解决显示问题) sudo apt install fonts-wqy…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Linux系统部署KES
1、安装准备 1.版本说明V008R006C009B0014 V008:是version产品的大版本。 R006:是release产品特性版本。 C009:是通用版 B0014:是build开发过程中的构建版本2.硬件要求 #安全版和企业版 内存:1GB 以上 硬盘…...

QT开发技术【ffmpeg + QAudioOutput】音乐播放器
一、 介绍 使用ffmpeg 4.2.2 在数字化浪潮席卷全球的当下,音视频内容犹如璀璨繁星,点亮了人们的生活与工作。从短视频平台上令人捧腹的搞笑视频,到在线课堂中知识渊博的专家授课,再到影视平台上扣人心弦的高清大片,音…...

Matlab实现任意伪彩色图像可视化显示
Matlab实现任意伪彩色图像可视化显示 1、灰度原始图像2、RGB彩色原始图像 在科研研究中,如何展示好看的实验结果图像非常重要!!! 1、灰度原始图像 灰度图像每个像素点只有一个数值,代表该点的亮度(或…...

echarts使用graphic强行给图增加一个边框(边框根据自己的图形大小设置)- 适用于无法使用dom的样式
pdf-lib https://blog.csdn.net/Shi_haoliu/article/details/148157624?spm1001.2014.3001.5501 为了完成在pdf中导出echarts图,如果边框加在dom上面,pdf-lib导出svg的时候并不会导出边框,所以只能在echarts图上面加边框 grid的边框是在图里…...
