QT-通信编码格式问题
这里写目录标题
- 一、项目场景
- 1.QT客户端与服务端通信时,转化步骤如下:
- 2.原数据示例
- 3.转化后数据
- 二、问题描述
- 1.采用Soap协议
- 2.采用HTTP协议
- 三、原因分析
- 四、解决方案
一、项目场景
1.QT客户端与服务端通信时,转化步骤如下:
- 1)客户端先将数据进行json序列化
- 2)利用SharpZipLib::GZip_Compress进行压缩
- 3)转化成Base64格式
2.原数据示例
"{ "Function" : "GetSysTime", "IsMutipleReturn" : false, "MessageContent" : "systime", "MessageSequence" : 0, "MsgGuid" : "", "Passport" : "IcsonPDA", "Totals" : 1, "Usage" : "User" }"
3.转化后数据
"H4sIAAAAAAAA/y2NwQ6CMBBEf6Xp2YNevRmMhAMJEfgAUkfSBLfY3R6I8d/tVo47783sx9hbIic+kDVnY2tIv/HgX7AHYxtuk/h1wR2SYjGe08LIqAXzNKMKJCApXd5Y9uJOe7wTyEHxUWOe6+QfxVatm5jXEP/1xnGg7npRMATJfzQ+5WvUreKMjGjN9wf8hZuAtgAAAA=="
二、问题描述
1.采用Soap协议
客户端采用Soap协议进行通信,服务端利用Zip和GZipInputStream可以解压成功,但接受到的数据不可读格式。在将数据转化为字符串类型后显示为乱码。
2.采用HTTP协议
客户端采用HTTP协议进行通信,服务端利用Zip和GZipInputStream解压报错。错误信息为Error GZIP header, second magic byte doesn’t match。
三、原因分析
猜测服务器在解析Soap协议时,按照byte数组进行解析,所以服务端解析会报错。
四、解决方案
1)先将byte数据转化为字符串;
2)再利用Convert.FromBase64String转换为8-bit unsigned byte array
Convert.FromBase64String(System.Text.Encoding.Default.GetString(requestbytes))
相关文章:

QT-通信编码格式问题
这里写目录标题 一、项目场景1.QT客户端与服务端通信时,转化步骤如下:2.原数据示例3.转化后数据 二、问题描述1.采用Soap协议2.采用HTTP协议 三、原因分析四、解决方案 一、项目场景 1.QT客户端与服务端通信时,转化步骤如下: 1&…...

一文了解Web3.0真实社交先驱ERA
Web2时代,少数科技巨头垄断了全球近60亿人口的网络社交数据,并用之为自己牟利,用户无法掌控个人数据,打破该局面逐渐成为共识,于是,不少人看到了Web3社交赛道蕴含的巨大机遇,标榜着去中心化和抗…...
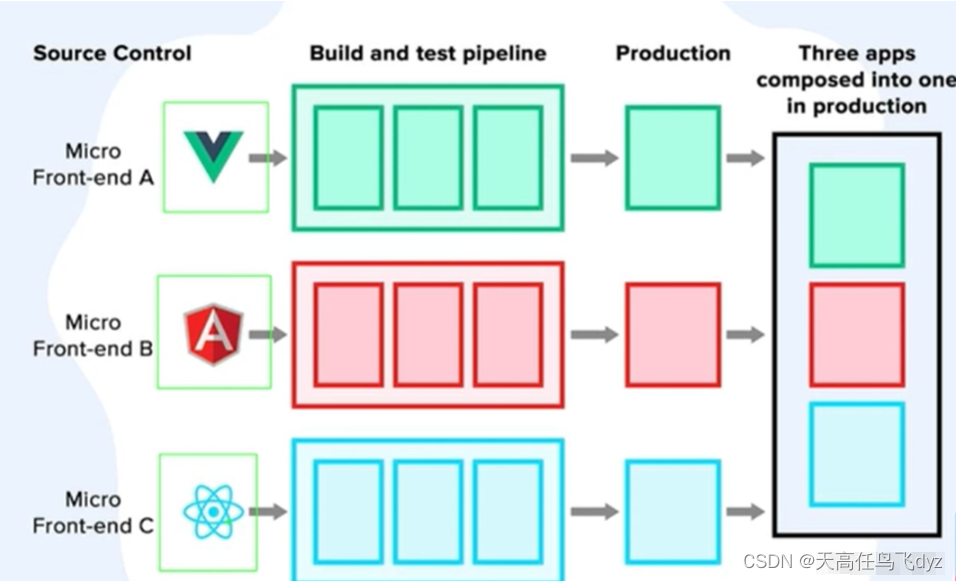
微前端(qiankun)vue3+vite
目录 一、什么是微前端 二、主应用接入 qiankun 1.按照qiankun插件 2.注册微应用引用 3.挂载容器 三、微应用接入 qiankun 1.vite.config.ts 2.main.ts ps:手动加载微应用方式 ps:为什么不用 iframe 一、什么是微前端 微前端是一种多个团队通过独…...
根据Ruoyi做二开
Ruoyi二开 前言菜单代码生成新建微服务网关添加微服务的路由 vue页面和对应的js文件js中方法的url和controller中方法的url总结 前言 之前写过一篇文章,若依微服务版本搭建,超详细,就介绍了怎么搭建若依微服务版本,我们使用若依就…...
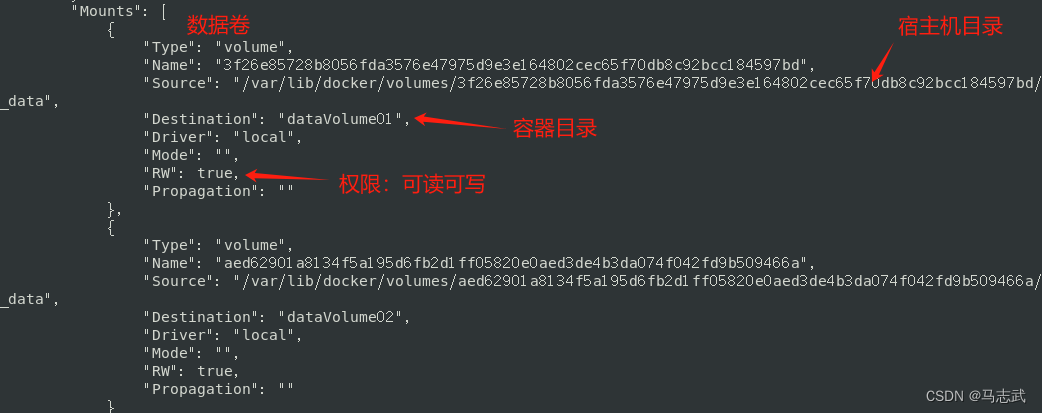
DockerFile的应用
DockerFile的应用 一、介绍1 构建的三步骤2 构建的过程 二、常用命令三、DockerFile案例1 创建DockerFile文件2 使用DockerFile文件构建镜像3 启动容器并验证 四 DockerFile添加数据卷 一、介绍 DockerFile是用来构建Docker镜像的构建文件,是由一系列命令和参数构成…...
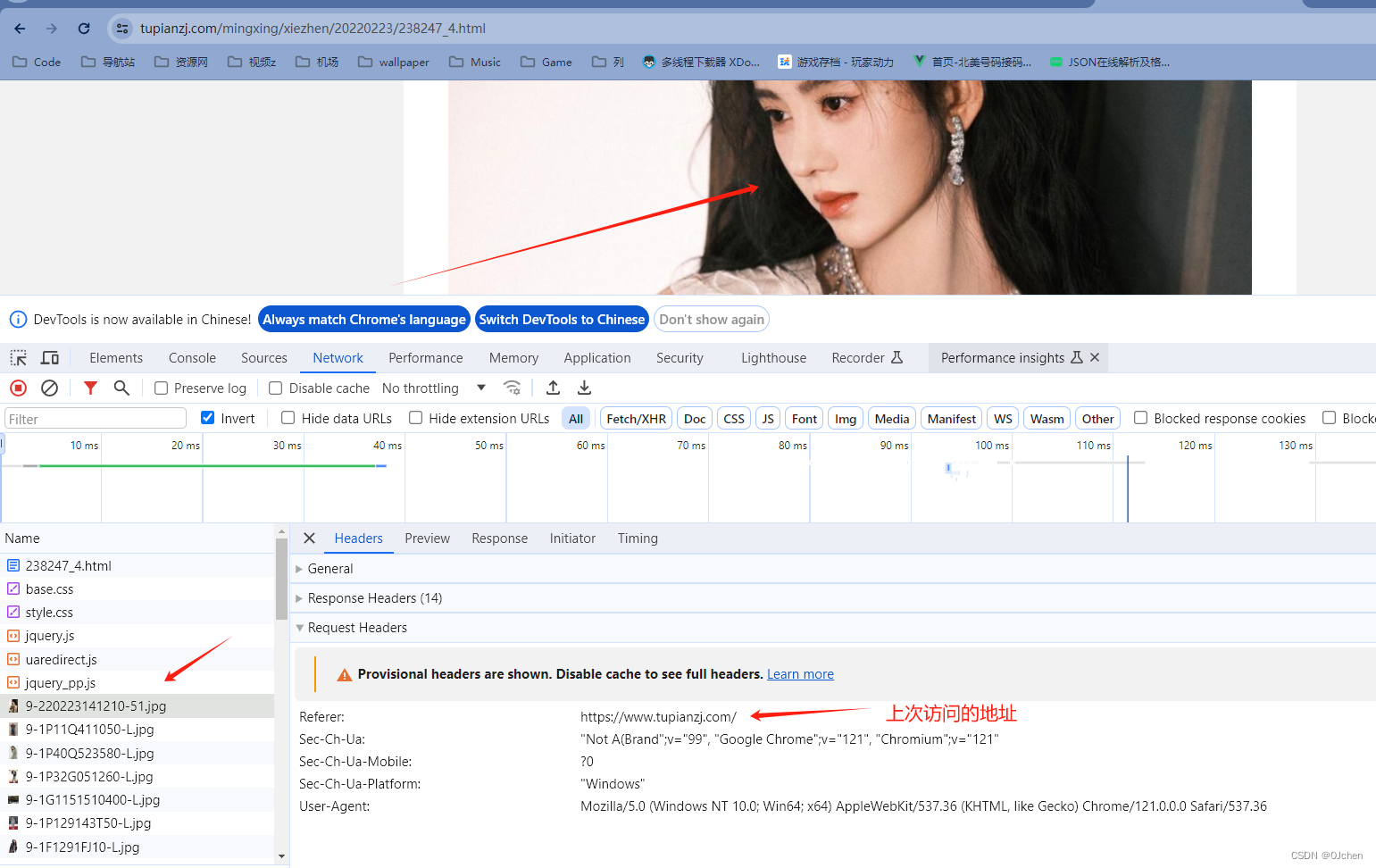
爬虫入门一
文章目录 一、什么是爬虫?二、爬虫基本流程三、requests模块介绍四、requests模块发送Get请求五、Get请求携带参数六、携带请求头七、发送post请求八、携带cookie方式一:放在请求头中方式二:放在cookie参数中 九、post请求携带参数十、模拟登…...

2024-02-16 web3-区块链-keypass记录
摘要: 2024-02-16 web3-区块链-keypass记录 文档: Introduction - Keypass Docs What is KEYPASS? - Keypass Docs What is KEYPASS? KeyPass Wallet is a new smart contract wallet that provides a secure and customizable registration…...

使用 JMimeMagic 在 Java 中识别文件类型
在 Java 中,我们可以使用 JMimeMagic 库来识别文件类型,尤其是在需要准确区分文件类型时。下面是一个简单的使用 JMimeMagic 的示例代码。 添加依赖 首先,在你的项目中添加 JMimeMagic 依赖。你可以在 Maven 项目中的 pom.xml 文件中加入以…...
yolov8源码解读Detect层
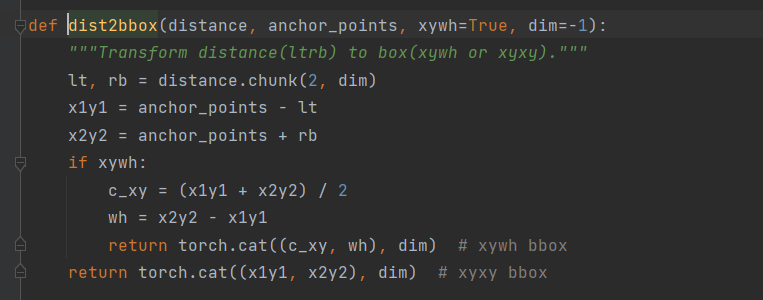
yolov8源码解读Detect层 Detect层解读网络各层解读及detect层后的处理 关于网络的backbone,head,以及detect层后处理,可以参考文章结尾博主的文章。 Detect层解读 先贴一下全部代码,下面一一解读。 class Detect(nn.Module):"""YOLOv8 …...
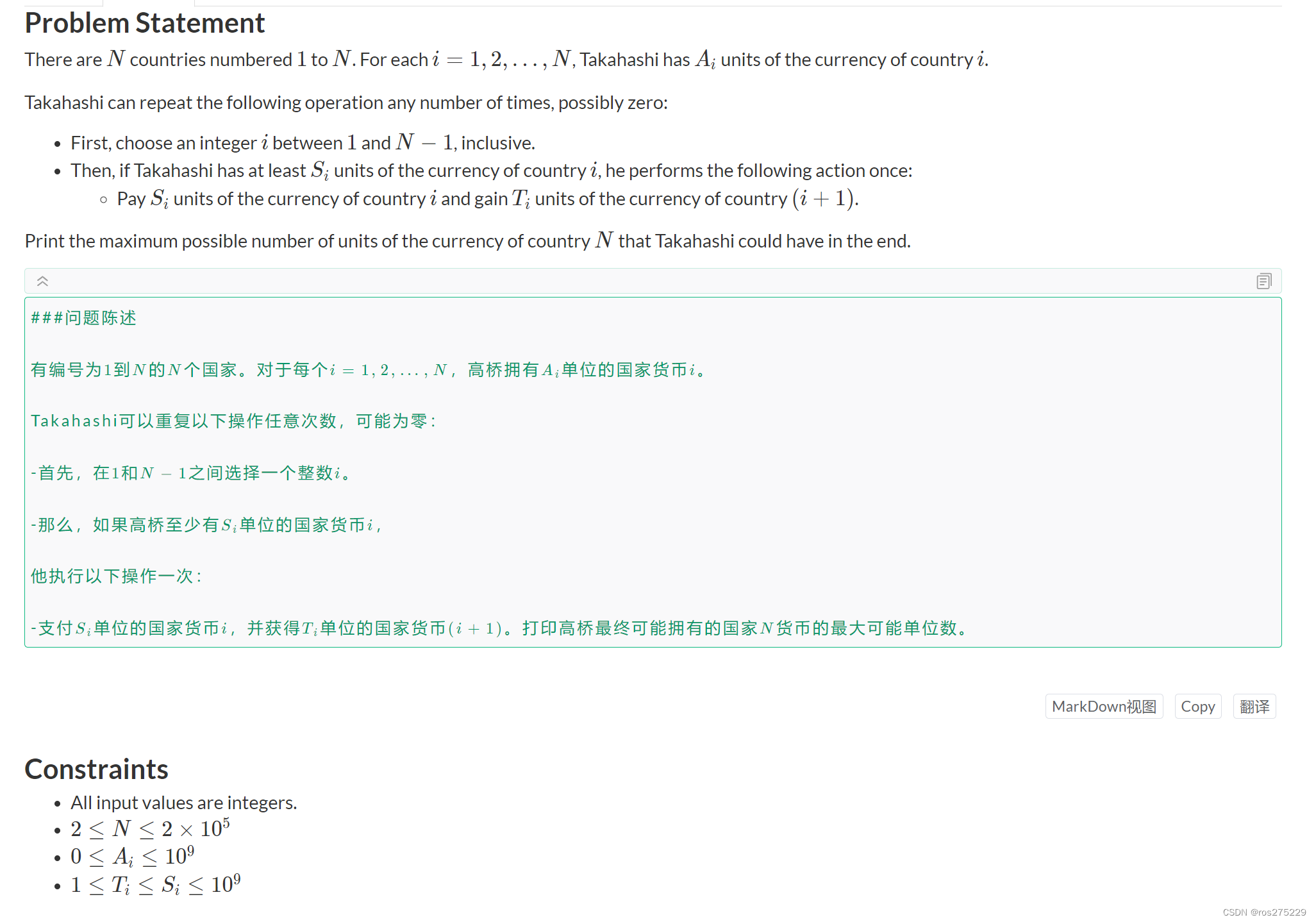
(AtCoder Beginner Contest 341)(A - D)
比赛地址 : Tasks - Toyota Programming Contest 2024#2(AtCoder Beginner Contest 341) A . Print 341 模拟就好了 , 先放一个 1 , 然后放 n 个 01 ; #include<bits/stdc.h> #define IOS ios::sync_with_stdio(0);cin.tie(0);cout…...

python Flask与微信小程序 统计管理
common/models/stat/StatDailyMember.py DROP TABLE IF EXISTS stat_daily_member;CREATE TABLE stat_daily_member (id int(11) unsigned NOT NULL AUTO_INCREMENT,date date NOT NULL COMMENT 日期,member_id int(11) NOT NULL DEFAULT 0 COMMENT 会员id,total_shared_count …...

光伏企业助力乡村振兴
光伏是一种利用太阳能生产电能的发电技术,属于可再生能源。近年来我国的光伏企业发展迅速,已经称霸全球,同时也为乡村振兴贡献了力量。 一、光伏企业助力乡村 1.推动农业发展 光伏发电和农业种植、畜牧、渔业、水产等有机结合,…...

root MUSIC 算法补充说明
root MUSIC 算法补充说明 多项式求根root MUSIC 算法原理如何从 2 M − 2 2M-2 2M−2 个根中确定 K K K 个根从复数域上观察 2 M − 2 2M-2 2M−2 个根的分布 这篇笔记是上一篇关于 root MUSIC 笔记的补充。 多项式求根 要理解 root MUSIC 算法,需要理解多项式求…...

关于Django的中间件使用说明。
目录 1.中间件2. 为什么要中间件?3. 具体使用中间件3.1 中间件所在的位置:在django的settings.py里面的MIDDLEWARE。3.2 中间件的创建3.3 中间件的使用 4. 展示成果 1.中间件 中间件的大概解释:在浏览器在请求服务器的时候,首先要…...

Chapter 8 - 15. Congestion Management in TCP Storage Networks
User Actions After learning the states of queue utilization, the following are the actions that admins and operators can take while using TCP transport for storage traffic. 了解了队列利用率的状态后,管理员和操作员在使用 TCP 传输存储流量时可以采取以下措施。…...

前端技巧之svg精灵图svg-sprite-loader
首先说明精灵图的必要性,其可以让我们只需要向服务器请求一次图片资源,就能加载很多图片,即能够减轻http请求造成的服务器压力。 然后这里要说明的是这个插件是webpack上面的,所以在vue2中比较好用,如果在vue3中&…...

IO线程-day2
1> 使用fread和fwrite完成两个文件的拷贝 程序: #define MAXSIZE 1024 #include<myhead.h>int main(int argc, char const *argv[]) {FILE *srcfpNULL;FILE *destfpNULL;if(!(srcfpfopen("pm.bmp","r")))PRINT_ERR("");if…...
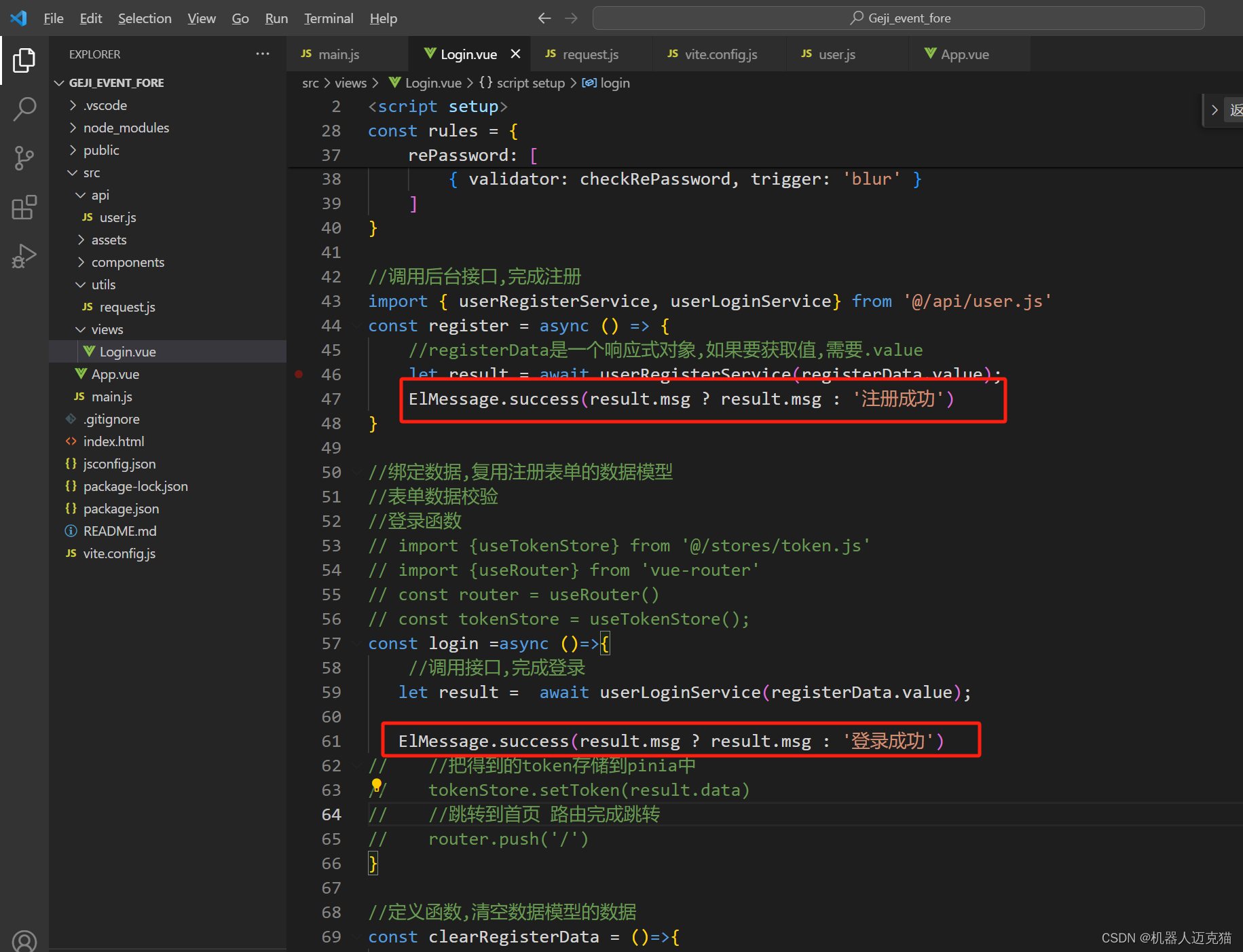
Spring Boot 笔记 024 登录页面
1.1 登录接口 //导入request.js请求工具 import request from /utils/request.js//提供调用注册接口的函数 export const userRegisterService (registerData)>{//借助于UrlSearchParams完成传递const params new URLSearchParams()for(let key in registerData){params.a…...

09_Java集合
一、Java集合框架概述 一方面, 面向对象语言对事物的体现都是以对象的形式,为了方便对多个对象的操作,就要对对象进行存储。另一方面,使用Array存储对象方面具有一些弊端,而Java 集合就像一种容器,可以动态…...

HCIA-HarmonyOS设备开发认证V2.0-3.2.轻量系统内核基础-软件定时器
目录 一、软件定时器基本概念二、软件定时器运行机制三、软件定时器状态四、软件定时器模式五、软件定时器开发流程六、软件定时器使用说明七、软件定时器接口八、代码分析(待续...)坚持就有收获 一、软件定时器基本概念 软件定时器,是基于系…...
结构体的进阶应用)
基于算法竞赛的c++编程(28)结构体的进阶应用
结构体的嵌套与复杂数据组织 在C中,结构体可以嵌套使用,形成更复杂的数据结构。例如,可以通过嵌套结构体描述多层级数据关系: struct Address {string city;string street;int zipCode; };struct Employee {string name;int id;…...

Linux相关概念和易错知识点(42)(TCP的连接管理、可靠性、面临复杂网络的处理)
目录 1.TCP的连接管理机制(1)三次握手①握手过程②对握手过程的理解 (2)四次挥手(3)握手和挥手的触发(4)状态切换①挥手过程中状态的切换②握手过程中状态的切换 2.TCP的可靠性&…...

MODBUS TCP转CANopen 技术赋能高效协同作业
在现代工业自动化领域,MODBUS TCP和CANopen两种通讯协议因其稳定性和高效性被广泛应用于各种设备和系统中。而随着科技的不断进步,这两种通讯协议也正在被逐步融合,形成了一种新型的通讯方式——开疆智能MODBUS TCP转CANopen网关KJ-TCPC-CANP…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

今日学习:Spring线程池|并发修改异常|链路丢失|登录续期|VIP过期策略|数值类缓存
文章目录 优雅版线程池ThreadPoolTaskExecutor和ThreadPoolTaskExecutor的装饰器并发修改异常并发修改异常简介实现机制设计原因及意义 使用线程池造成的链路丢失问题线程池导致的链路丢失问题发生原因 常见解决方法更好的解决方法设计精妙之处 登录续期登录续期常见实现方式特…...

腾讯云V3签名
想要接入腾讯云的Api,必然先按其文档计算出所要求的签名。 之前也调用过腾讯云的接口,但总是卡在签名这一步,最后放弃选择SDK,这次终于自己代码实现。 可能腾讯云翻新了接口文档,现在阅读起来,清晰了很多&…...

4. TypeScript 类型推断与类型组合
一、类型推断 (一) 什么是类型推断 TypeScript 的类型推断会根据变量、函数返回值、对象和数组的赋值和使用方式,自动确定它们的类型。 这一特性减少了显式类型注解的需要,在保持类型安全的同时简化了代码。通过分析上下文和初始值,TypeSc…...
)
安卓基础(Java 和 Gradle 版本)
1. 设置项目的 JDK 版本 方法1:通过 Project Structure File → Project Structure... (或按 CtrlAltShiftS) 左侧选择 SDK Location 在 Gradle Settings 部分,设置 Gradle JDK 方法2:通过 Settings File → Settings... (或 CtrlAltS)…...

通过MicroSip配置自己的freeswitch服务器进行调试记录
之前用docker安装的freeswitch的,启动是正常的, 但用下面的Microsip连接不上 主要原因有可能一下几个 1、通过下面命令可以看 [rootlocalhost default]# docker exec -it freeswitch fs_cli -x "sofia status profile internal"Name …...

ZYNQ学习记录FPGA(一)ZYNQ简介
一、知识准备 1.一些术语,缩写和概念: 1)ZYNQ全称:ZYNQ7000 All Pgrammable SoC 2)SoC:system on chips(片上系统),对比集成电路的SoB(system on board) 3)ARM:处理器…...
