代码随想录算法训练营day17||二叉树part04、110.平衡二叉树 、257. 二叉树的所有路径 、404.左叶子之和
110.平衡二叉树 (优先掌握递归)
题目:给定一个二叉树,判断它是否是高度平衡的二叉树。
本题中,一棵高度平衡二叉树定义为:一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过1。
示例 1:给定二叉树 [3,9,20,null,null,15,7] 返回 true 。 示例2:返回false


题外话
咋眼一看这道题目和104.二叉树的最大深度 (opens new window)很像,其实有很大区别。
这里强调一波概念:
- 二叉树节点的深度:指从根节点到该节点的最长简单路径边的条数。
- 二叉树节点的高度:指从该节点到叶子节点的最长简单路径边的条数。
但leetcode中强调的深度和高度很明显是按照节点来计算的,如图:

注意:关于根节点的深度究竟是1 还是 0,不同的地方有不一样的标准,leetcode的题目中都是以节点为一度,即根节点深度是1。但维基百科上定义用边为一度,即根节点的深度是0,我们暂时以leetcode为准(毕竟要在这上面刷题)。
因为求深度可以从上到下去查 所以需要前序遍历(中左右),而高度只能从下到上去查,所以只能后序遍历(左右中)
有的同学一定疑惑,为什么104.二叉树的最大深度 (opens new window)中求的是二叉树的最大深度,也用的是后序遍历。
那是因为代码的逻辑其实是求的根节点的高度,而根节点的高度就是这棵树的最大深度,所以才可以使用后序遍历。
本题思路:(此时大家应该明白了既然要求比较高度,必然是要后序遍历。)采用递归法
递归三步曲分析:
1.明确递归函数的参数和返回值
参数:当前传入节点。 返回值:以当前传入节点为根节点的树的高度。
那么如何标记左右子树是否差值大于1呢?
如果当前传入节点为根节点的二叉树已经不是二叉平衡树了,还返回高度的话就没有意义了。
所以如果已经不是二叉平衡树了,可以返回-1 来标记已经不符合平衡树的规则了。
2.明确终止条件
递归的过程中依然是遇到空节点了为终止,返回0,表示当前节点为根节点的树高度为0
3.明确单层递归的逻辑
如何判断以当前传入节点为根节点的二叉树是否是平衡二叉树呢?当然是其左子树高度和其右子树高度的差值。
分别求出其左右子树的高度,然后如果差值小于等于1,则返回当前二叉树的高度,否则返回-1,表示已经不是二叉平衡树了。
class Solution {public boolean isBalanced(TreeNode root) {//递归法return getHeight(root) != -1;}private int getHeight(TreeNode root){if(root == null ) return 0;int leftHeight = getHeight(root.left);if(leftHeight == -1) return -1;int rightHeight = getHeight(root.right);if(rightHeight == -1) return -1;//左右子树高度差大于1,return -1表示已经不是平衡二叉树了if(Math.abs(leftHeight - rightHeight) > 1) {return -1;}return Math.max(leftHeight,rightHeight) + 1;}
}257. 二叉树的所有路径 (优先掌握递归)
这是大家第一次接触到回溯的过程, 我在视频里重点讲解了 本题为什么要有回溯,已经回溯的过程。 如果对回溯 似懂非懂,没关系, 可以先有个印象。
题目:给定一个二叉树,返回所有从根节点到叶子节点的路径。
说明: 叶子节点是指没有子节点的节点。

思路
这道题目要求从根节点到叶子的路径,所以需要前序遍历,这样才方便让父节点指向孩子节点,找到对应的路径。
在这道题目中将第一次涉及到回溯,因为我们要把路径记录下来,需要回溯来回退一个路径再进入另一个路径。
前序遍历以及回溯的过程如图:

class Solution {public List<String> binaryTreePaths(TreeNode root) {//递归法List<String> res = new ArrayList<>(); //用于存储最终结果集的List,其中每个元素都是一个表示路径的字符串。if(root == null) return res;List<Integer> paths = new ArrayList<>();//用于在递归过程中构建路径的List,其中每个元素都是二叉树节点的值。traversal(root,paths,res);return res;}//traversal 方法是递归的核心部分,它接受当前节点、路径列表和结果列表作为参数。private void traversal(TreeNode root,List<Integer> paths,List<String> res){paths.add(root.val); //前序遍历,中!//遇到叶子节点时(左右子树都为空的节点)if(root.left == null && root.right == null){//输出StringBuilder sb = new StringBuilder();//创建一个StringBuilder对象sb用来拼接字符串,速度更快//遍历路径列表,将paths中的元素按顺序连接成一个路径,并将该路径添加到res集合中。for(int i = 0;i < paths.size()-1; i++){ sb.append(paths.get(i)).append("->");}sb.append(paths.get(paths.size() - 1));//记录最后一个节点res.add(sb.toString());//收集一个路径return;}//递归和回溯是同时进行的,所以要放在同一个花括号里if(root.left != null){ traversal(root.left,paths,res); //左paths.remove(paths.size() - 1); //回溯}if(root.right != null){traversal(root.right,paths,res); //右paths.remove(paths.size() - 1); //回溯}}
}注意:
traversal方法:
traversal方法是递归的核心部分。它接受当前节点、路径列表和结果列表作为参数。- 将当前节点的值添加到路径列表中。
- 如果当前节点是叶子节点(左右子节点都为空),则执行以下操作:
- 创建一个
StringBuilder对象sb。- 通过遍历路径列表,将节点值连接成路径字符串,并使用
->分隔。- 将路径字符串添加到结果列表中。
- 无论当前节点是否为叶子节点,都会递归地对左子节点和右子节点执行相同的操作(如果存在的话)。在递归之后,会通过
paths.remove(paths.size() - 1);进行回溯,移除刚刚添加的节点值,以恢复到上一层的状态。
这行代码
paths.remove(paths.size() - 1);是在回溯过程中使用的。在递归遍历左子树或右子树之后,程序需要回到当前节点的父节点,继续遍历其他子节点或者回溯到更上层的节点。
因为
paths列表记录了从根节点到当前节点的路径,当递归返回到父节点时,需要将当前节点从路径中移除,以便继续探索其他分支或者回溯到更上层的节点,保证paths列表中记录的是当前路径上的节点序列。这就是为什么在回溯时,需要移除paths列表中的最后一个元素的原因。
class Solution {//方式二:递归法,精简版,并隐藏了回溯过程List<String> result = new ArrayList<>();//用于存储最终结果集的List,其中每个元素都是一个表示路径的字符串。public List<String> binaryTreePaths(TreeNode root) {traversal(root, "");return result;}public void traversal(TreeNode node, String sb) {//当前节点为空时if (node == null)return;//当前节点为 叶子节点时,将当前节点的值添加到字符串s后面,并将整个字符串添加到结果列表中。if (node.left == null && node.right == null) {result.add(new StringBuilder(sb).append(node.val).toString()); //中return;}//创建一个临时字符串 tmp,它是在字符串s后面添加了当前节点的值和箭头 ->。String tmp = new StringBuilder(sb).append(node.val).append("->").toString(); traversal(node.left, tmp); //左traversal(node.right, tmp); //右}
}
traversal方法:
- 如果当前节点为空,直接返回。
- 如果当前节点是叶子节点(左右子节点都为空),则将当前节点的值添加到字符串
s后面,并将整个字符串添加到结果列表中。- 创建一个临时字符串
tmp,它是在字符串s后面添加了当前节点的值和->。- 然后分别对左子节点和右子节点递归调用
traversal方法,并将临时字符串tmp作为参数传递下去。总体逻辑:
- 通过递归调用
traversal方法,在每个叶子节点处将路径字符串添加到结果列表中。- 递归过程中使用临时字符串来构建路径,简化了代码的实现。
这种方法的核心思想与之前的代码类似,都是通过递归遍历二叉树,并在叶子节点处构建路径字符串。但是,这个精简版的代码隐藏了回溯过程,通过临时字符串tmp和直接在叶子节点处添加路径字符串来简化了代码的结构。
404.左叶子之和 (优先掌握递归)
其实本题有点文字游戏,搞清楚什么是左叶子,剩下的就是二叉树的基本操作。

思路
首先要注意是判断左叶子,不是二叉树左侧节点,所以不要上来想着层序遍历。
因为题目中其实没有说清楚左叶子究竟是什么节点,那么我来给出左叶子的明确定义:节点A的左孩子不为空,且左孩子的左右孩子都为空(说明是叶子节点),那么A节点的左孩子为左叶子节点
大家思考一下如下图中二叉树,左叶子之和究竟是多少? 没有左叶子!

再看这个图的左叶子之和是多少?
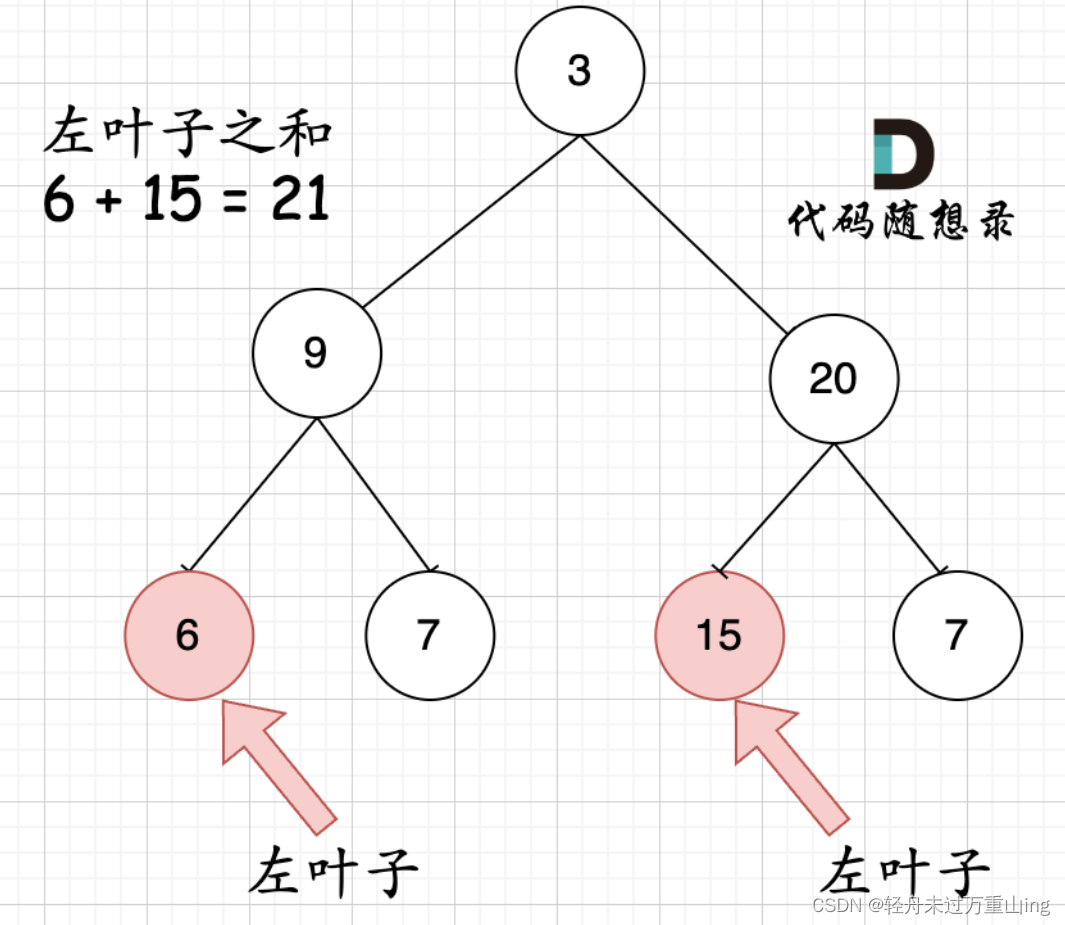
相信通过这两个图,大家对最左叶子的定义有明确理解了。
那么判断当前节点是不是左叶子是无法判断的,必须要通过节点的父节点来判断其左孩子是不是左叶子。
如果该节点的左节点不为空,该节点的左节点的左节点为空,该节点的左节点的右节点为空,则找到了一个左叶子,判断代码如下:
if (node->left != NULL && node->left->left == NULL && node->left->right == NULL) {左叶子节点处理逻辑
}递归法
递归的遍历顺序为后序遍历(左右中),是因为要通过递归函数的返回值来累加求取左叶子数值之和。
递归三部曲:
1.确定递归函数的参数和返回值
判断一个树的左叶子节点之和,那么一定要传入树的根节点,递归函数的返回值为数值之和,所以为int
使用题目中给出的函数就可以了。
2.确定终止条件
如果遍历到空节点,那么左叶子值一定是0
注意,只有当前遍历的节点是父节点,才能判断其子节点是不是左叶子。 所以如果当前遍历的节点是叶子节点,那其左叶子也必定是0,那么终止条件为:
if (root == NULL) return 0;
if (root->left == NULL && root->right== NULL) return 0; //其实这个也可以不写,如果不写不影响结果,但就会让递归多进行了一层。3.确定单层递归的逻辑
当遇到左叶子节点的时候,记录数值,然后通过递归求取左子树左叶子之和,和 右子树左叶子之和,相加便是整个树的左叶子之和。
class Solution {public int sumOfLeftLeaves(TreeNode root) {//递归法,后序遍历if(root == null) return 0;int leftValue = sumOfLeftLeaves(root.left); //左int rightValue = sumOfLeftLeaves(root.right); //右int midValue = 0;//判断左叶子的关键语句,该节点的左节点不为空,但左节点的左节点和左节点的右节点为空! //则把该节点的左节点赋值给midValueif(root.left != null && root.left.left == null && root.left.right == null){midValue = root.left.val;}int sum = midValue + leftValue + rightValue; //中return sum;}
}相关文章:

代码随想录算法训练营day17||二叉树part04、110.平衡二叉树 、257. 二叉树的所有路径 、404.左叶子之和
注意:迭代法,可以先过,二刷有精力的时候 再去掌握迭代法。 110.平衡二叉树 (优先掌握递归) 再一次涉及到,什么是高度,什么是深度,可以巩固一下。 题目:给定一个二叉树&am…...

three.js 3D可视化地图
threejs地图 可视化地图——three.js实现 this.provinceInfo document.getElementById(provinceInfo); // 渲染器 this.renderer new THREE.WebGLRenderer({antialias: true }); this.renderer.setSize(window.innerWidth, window.innerHeight); this.container.appendChild…...

Unity所有关于旋转的方法详解
前言:欧拉角和四元数的简单描述 我们在Inspector面板上看到的rotation其实是欧拉角, 我们将Inspector面板设置成Debug模式,此时看到的local Rotation才是四元数。 Unity中的欧拉旋转是按照Z-X-Y顺规执行的旋转,一组欧拉旋转过程中…...

Vue3
目录 一、 Vue3简介 1. 性能的提升 2. 源码的升级 3. 拥抱TypeScript 4. 新的特性 二、 创建Vue3工程 1. 基于 vue-cli 创建 2. 基于 vite 创建(推荐) 3. 一个简单的效果 三、Vue3核心语法 1. OptionsAPI 与 CompositionAPI (1)Options API …...
浅谈业务场景中缓存的使用
浅谈缓存 一、背景二、缓存分类1.本地缓存2.分布式缓存 三、缓存读写模式1.读请求2.写请求 四、缓存穿透1.缓存空对象2.请求校验3.请求来源限制4.布隆过滤器 五、缓存击穿1.改变过期时间2.串行访问数据库 六、缓存雪崩1.避免集中过期2.提前更新缓存 七、缓存与数据库一致性1.设…...

Itext生成pdf文件,html转pdf时中文一直显示不出来
之前使用freemark模板渲染ftl页面,转出的pdf中,css2有些样式好像不支持,比较常用的居中样式都没有效果,text-align:center 改造成使用html页面来转pdf,css2的样式可以生效,itext是不支持css3的弹性布局的ITextRenderer pdfRendere…...

题目 1138: C语言训练-求矩阵的两对角线上的元素之和
问题描述: 求矩阵的两对角线上的元素之和 样例输入: 3 1 2 3 4 5 6 7 8 9 样例输出: 25 问题分析: 因为奇数阶矩阵的主对角线和副对角线上的元素有重复,偶数阶矩阵的主对角线和副对角线上的元素无重复&#x…...
第6讲自定义icon实现
自定义icon实现 component下新建SvgIcon目录,再新建index.vue 定义svg-icon组件 <template><svg class"svg-icon" aria-hidden"true"><use :xlink:href"iconName"></use></svg> </template>&…...

花费200元,我用全志H616和雪糕棒手搓了一台可UI交互的视觉循迹小车
常见的视觉循迹小车都具备有路径识别、轨迹跟踪、转向避障、自主决策等基本功能,如果不采用红外避障的方案,那么想要完全满足以上这些功能,摄像头、电机、传感器这类关键部件缺一不可,由此一来小车成本也就难以控制了。 但如果&a…...

AUTOSAR OS TASK
什么是TASK? 我们在裸机中跑代码,程序永远只能单活动流水执行,当程序需要等待的时候,CPU就一直在waiting状态,无法高效的利用CPU,这个时候就引入了并发运行需求。一个系统能同时执行多个不同活动的系统叫做并发系统。其中这个系统中的每个并发执行的活动都由TASK(任务)…...
陇剑杯 2021刷题记录
题目位置:https://www.nssctf.cn/上有 陇剑杯 2021 1. 签到题题目描述分析答案小结 2. jwt问1析1答案小结 问2析2答案小结 问3析3答案 问4析4答案 问5析5答案 问6析6答案 3. webshell问1析1答案 问2析2答案 问3析3答案 1. 签到题 题目描述 此时正在进行的可能是_…...
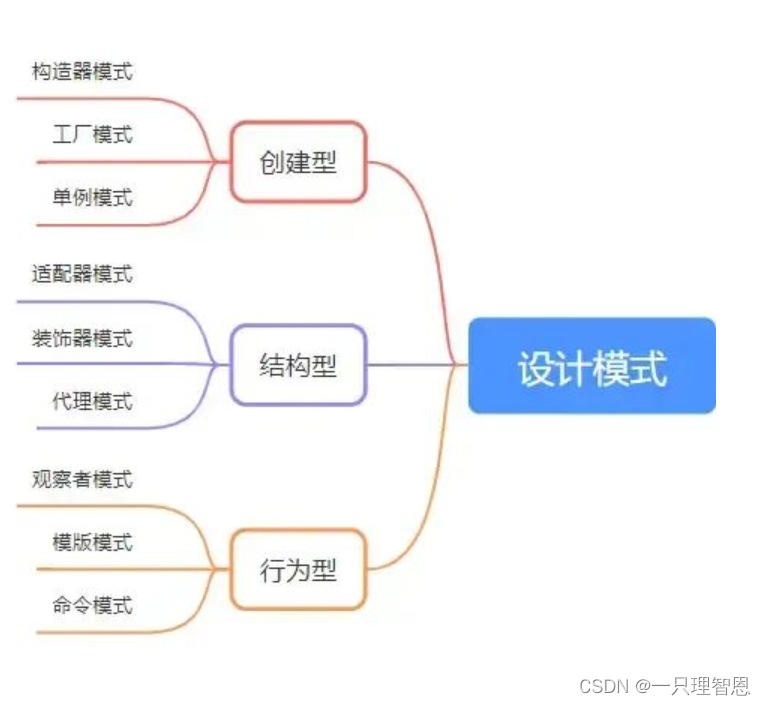
前端常见的设计模式
说到设计模式,大家想到的就是六大原则,23种模式。这么多模式,并非都要记住,但作为前端开发,对于前端出现率高的设计模式还是有必要了解并掌握的,浅浅掌握9种模式后,整理了这份文章。 六大原则&…...
OpenAI视频生成模型Sora的全面解析:从ViViT、扩散Transformer到NaViT、VideoPoet
前言 真没想到,距离视频生成上一轮的集中爆发(详见《Sora之前的视频生成发展史:从Gen2、Emu Video到PixelDance、SVD、Pika 1.0》)才过去三个月,没想OpenAI一出手,该领域又直接变天了 自打2.16日OpenAI发布sora以来(其开发团队包…...

3个密码学相关的问题
一、离散对数问题(Discrete Logarithm Problem, DLP) 问题描述:给定 有限阿贝尓群 G中的2个元素a和b,找出最小的正整数x满足:b a ^^ x (或者证明这样的x不存在)。 二、阶数问题(O…...

5G网络eMBB、uRLLC、mMTC
ITU(国际电信联盟)于2015年9月正式定义了5G的三大应用场景:eMBB(增强型移动宽带)、uRLLC(低时延高可靠通信)、mMTC(海量物联网通信)。 eMBB是4G MBB(移动宽带…...
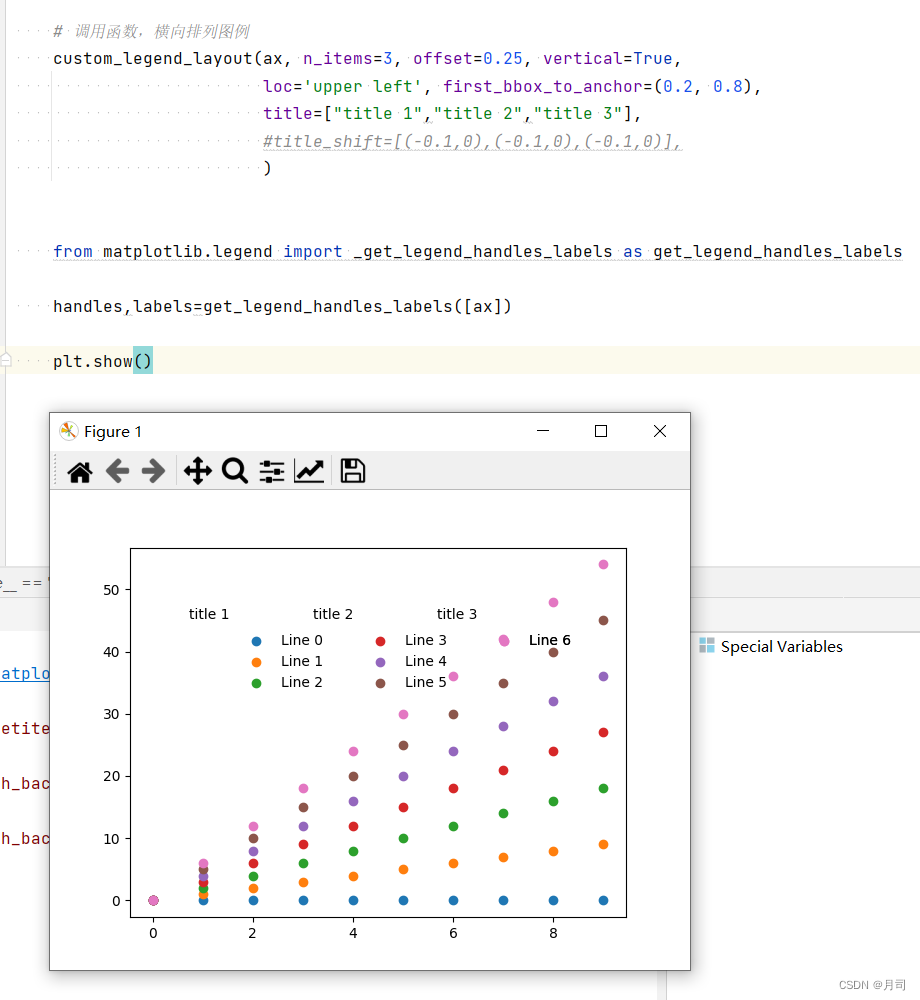
matplotlib图例使用案例1.1:在不同行或列的图例上添加title
我们将图例进行行显示或者列显示后,只能想继续赋予不同行或者列不同的title来进行分类。比较简单的方式,就是通过ax.annotate方法添加标签,这样方法复用率比较低,每次使用都要微调ax.annotate的显示位置。比较方便的方法是在案例1…...

nginx 日志改为json格式
nginx 日志改为json格式 场景描述效果变更旧样式新样式 场景描述 正常使用nginx时,使用默认的日志输出格式,对于后续日志接入其他第三方日志收集、清洗环节,因分隔符问题可能不是很友好。 xxxx - - [19/Feb/2024:11:16:48 0800] "GET …...
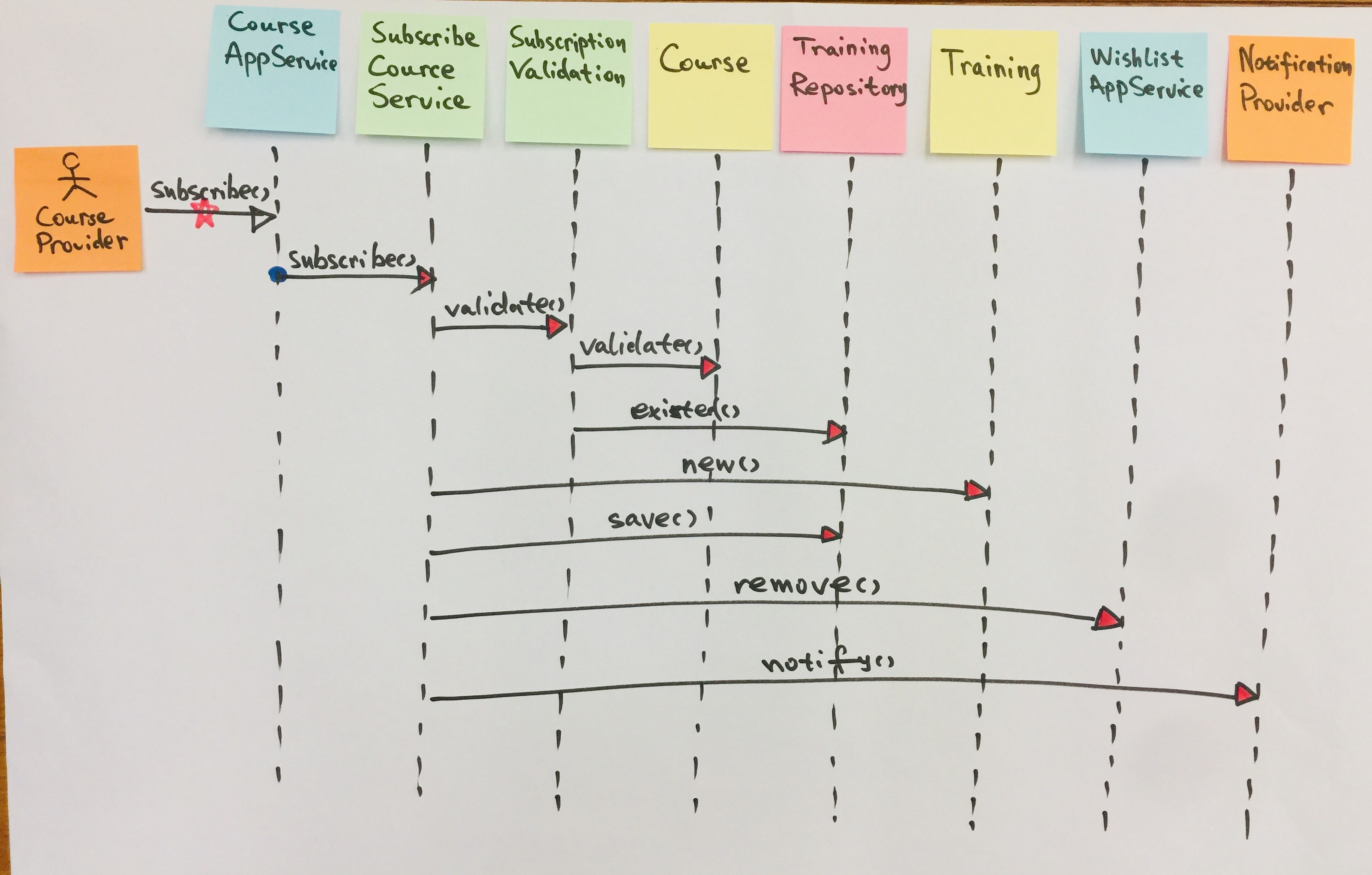
【DDD】学习笔记-应用服务
Eric Evans 为运用领域驱动设计的系统架构划定了层次,在领域层和展现层之间引入了应用层(Application Layer):“应用层要尽量简单,不包含业务规则或者知识,而只为下一层(指领域层)中…...
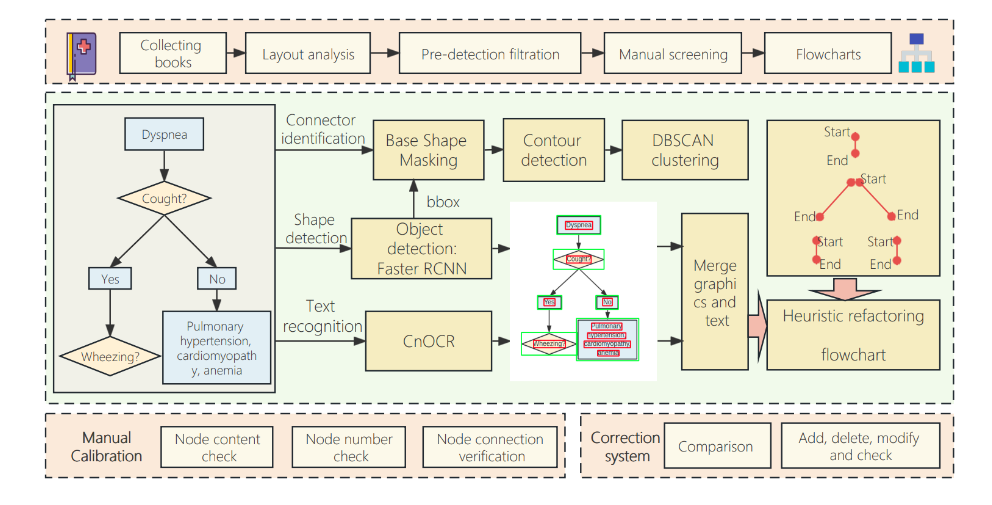
【医学大模型】MEDDM LLM-Executable CGT 结构化医学知识: 将临床指导树结构化,便于LLM理解和应用
MEDDM LLM-Executable CGT 结构化医学知识: 将临床指导树结构化,便于LLM理解和应用 提出背景对比传统医学大模型流程步骤临床指导树流程图识别临床决策支持系统 总结解决方案设计数据收集与处理系统实施临床决策支持 提出背景 论文:https://arxiv.org/p…...

YOLOV8改进系列指南
基于Ultralytics的YOLOV8改进项目.(69.9) 为了感谢各位对V8项目的支持,本项目的赠品是yolov5-PAGCP通道剪枝算法.具体使用教程 专栏改进汇总 二次创新系列 ultralytics/cfg/models/v8/yolov8-RevCol.yaml 使用(ICLR2023)Reversible Column Networks对yolov8主干进行重设计,里…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

什么是库存周转?如何用进销存系统提高库存周转率?
你可能听说过这样一句话: “利润不是赚出来的,是管出来的。” 尤其是在制造业、批发零售、电商这类“货堆成山”的行业,很多企业看着销售不错,账上却没钱、利润也不见了,一翻库存才发现: 一堆卖不动的旧货…...

在四层代理中还原真实客户端ngx_stream_realip_module
一、模块原理与价值 PROXY Protocol 回溯 第三方负载均衡(如 HAProxy、AWS NLB、阿里 SLB)发起上游连接时,将真实客户端 IP/Port 写入 PROXY Protocol v1/v2 头。Stream 层接收到头部后,ngx_stream_realip_module 从中提取原始信息…...

使用van-uploader 的UI组件,结合vue2如何实现图片上传组件的封装
以下是基于 vant-ui(适配 Vue2 版本 )实现截图中照片上传预览、删除功能,并封装成可复用组件的完整代码,包含样式和逻辑实现,可直接在 Vue2 项目中使用: 1. 封装的图片上传组件 ImageUploader.vue <te…...
)
Java入门学习详细版(一)
大家好,Java 学习是一个系统学习的过程,核心原则就是“理论 实践 坚持”,并且需循序渐进,不可过于着急,本篇文章推出的这份详细入门学习资料将带大家从零基础开始,逐步掌握 Java 的核心概念和编程技能。 …...

C++使用 new 来创建动态数组
问题: 不能使用变量定义数组大小 原因: 这是因为数组在内存中是连续存储的,编译器需要在编译阶段就确定数组的大小,以便正确地分配内存空间。如果允许使用变量来定义数组的大小,那么编译器就无法在编译时确定数组的大…...

打手机检测算法AI智能分析网关V4守护公共/工业/医疗等多场景安全应用
一、方案背景 在现代生产与生活场景中,如工厂高危作业区、医院手术室、公共场景等,人员违规打手机的行为潜藏着巨大风险。传统依靠人工巡查的监管方式,存在效率低、覆盖面不足、判断主观性强等问题,难以满足对人员打手机行为精…...

Golang——9、反射和文件操作
反射和文件操作 1、反射1.1、reflect.TypeOf()获取任意值的类型对象1.2、reflect.ValueOf()1.3、结构体反射 2、文件操作2.1、os.Open()打开文件2.2、方式一:使用Read()读取文件2.3、方式二:bufio读取文件2.4、方式三:os.ReadFile读取2.5、写…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...

在 Spring Boot 项目里,MYSQL中json类型字段使用
前言: 因为程序特殊需求导致,需要mysql数据库存储json类型数据,因此记录一下使用流程 1.java实体中新增字段 private List<User> users 2.增加mybatis-plus注解 TableField(typeHandler FastjsonTypeHandler.class) private Lis…...
