【剑指Offer】JZ14--剪绳子
剪绳子详解
- 1.问题描述
- 2.解题思路
- 3.具体实现
1.问题描述

2.解题思路
- 首先想到的思路:因为是求乘积的最大值,所以如果截取剩下的是1,那还是它本身就没有意义。从此出发,考虑绳子长度是2、3、4、5…通过穷举法来找规律。
值–》拆分–》最大乘积
2 --》0+2 1+1 --》2
3 --》0+3 1+2 --》3
4 --》1+3 2+2 --》4
5 --》1+4 2+3 --》6
6 --》1+5 2+4 3+3 --》9
7 --》1+6 2+5 3+4 --》12
8 --》1+7 2+6 3+5 4+4 --》18
发现:2,、3、4最大值都是他们本身,5的最大值是可能拆成的数A+B的A的最大值与B的最大值的乘积,由此或许会联想到动态规划。但是用动态规划比较复杂,首先需要将其拆分成两项(一直拆到有值/2的数出现),接着需要还需要对每个拆分项进行拆分(出口就是2、3、4)。
2.于是我接着思考,是否还有哪些规律可以利用。因此我从最大值之间的联系与绳子长度进行分析
发现:最大值一般都是在 n/2 附近出现的,再进一步发现都是通过拆成3来实现最大值,一直拆到最后一个值大于1,因为拆成1没有意义。通过这个规律会发现代码实现就很容易了
6 3+3 3+2+1–>9 3+2
7 3+4 3+2+2–>12 3+2+2
8 1+7 2+6 3+5 4+4–>18 3+3+2
9 1+8 2+7 3+6 4+5–>27 3+3+3
3.具体实现
package offer230304;
import java.util.*;
/*** 剪绳子* 长度是n >1* 剪成整数长的m段 >1 <=n`在这里插入代码片`* 每段绳子的长度是 k[1]....k[m]* * 可以想为是一个* 1* 2 1+1 0+2 --》2* 3 1+2 -->3* 4 2+2 1+3 -->4* 5 2+3 1+4-->6* 6 3+3 3+2+1-->9 3+2* 7 3+4 3+2+2-->12 3+2+2* 8 1+7 2+6 3+5 4+4-->18 3+3+2* 9 1+8 2+7 3+6 4+5-->27 3+3+3* 10 1+9 2+8 3+7 4+6 5+5-->36 3+3+4* 11 3+8 4+7 5+6 -->54 3+3+3+2* 拆成3而且最后不能是1,因为拆成1没有意义* 1--1 2--2 3--3* 4--4 3+1(3后面剩下的不能是1,最少是2)* 》3的值似乎都是和3有关* @author wen yang* @230304*/
public class JZ14 {public static void main(String[] args) {// TODO Auto-generated method stub//被我找到规律的Scanner scanner=new Scanner(System.in);int target = scanner.nextInt();//将它以3进行拆分,剩下的如果不大于1,那就不拆了ArrayList<Integer> partList = new ArrayList<>();System.out.println(getMaxMul(target, partList));}public static int getMaxMul(int target,ArrayList<Integer> partList) {int maxMul=1;int partTarget=target;//判断是否大于4,直接list的大小/*if(target<=4) {return maxMul*target;}*///进行拆分剩下的如果不大于1,那就不拆了while(partTarget-3>1) {partList.add(3);partTarget-=3;}//判断是否大于4,if(partList.size()==0) {return maxMul*target;}//拆到最后的也加入集合中partList.add(partTarget);for(int i=0;i<partList.size();i++) {maxMul*=partList.get(i);}return maxMul;}}
相关文章:

【剑指Offer】JZ14--剪绳子
剪绳子详解1.问题描述2.解题思路3.具体实现1.问题描述 2.解题思路 首先想到的思路:因为是求乘积的最大值,所以如果截取剩下的是1,那还是它本身就没有意义。从此出发,考虑绳子长度是2、3、4、5…通过穷举法来找规律。 值–》拆分–…...
raspberry pi播放音视频
文章目录目的QMediaPlayerGStreamerwhat is GStreamer体系框架优势omxplayerwhat is omxplayercommand Linekey bindings运行过程中错误ALSA目的 实现在树莓派下外接扬声器, 播放某段音频, 进行回音测试。 QMediaPlayer 首先我的安装是5.11版本。 优先…...
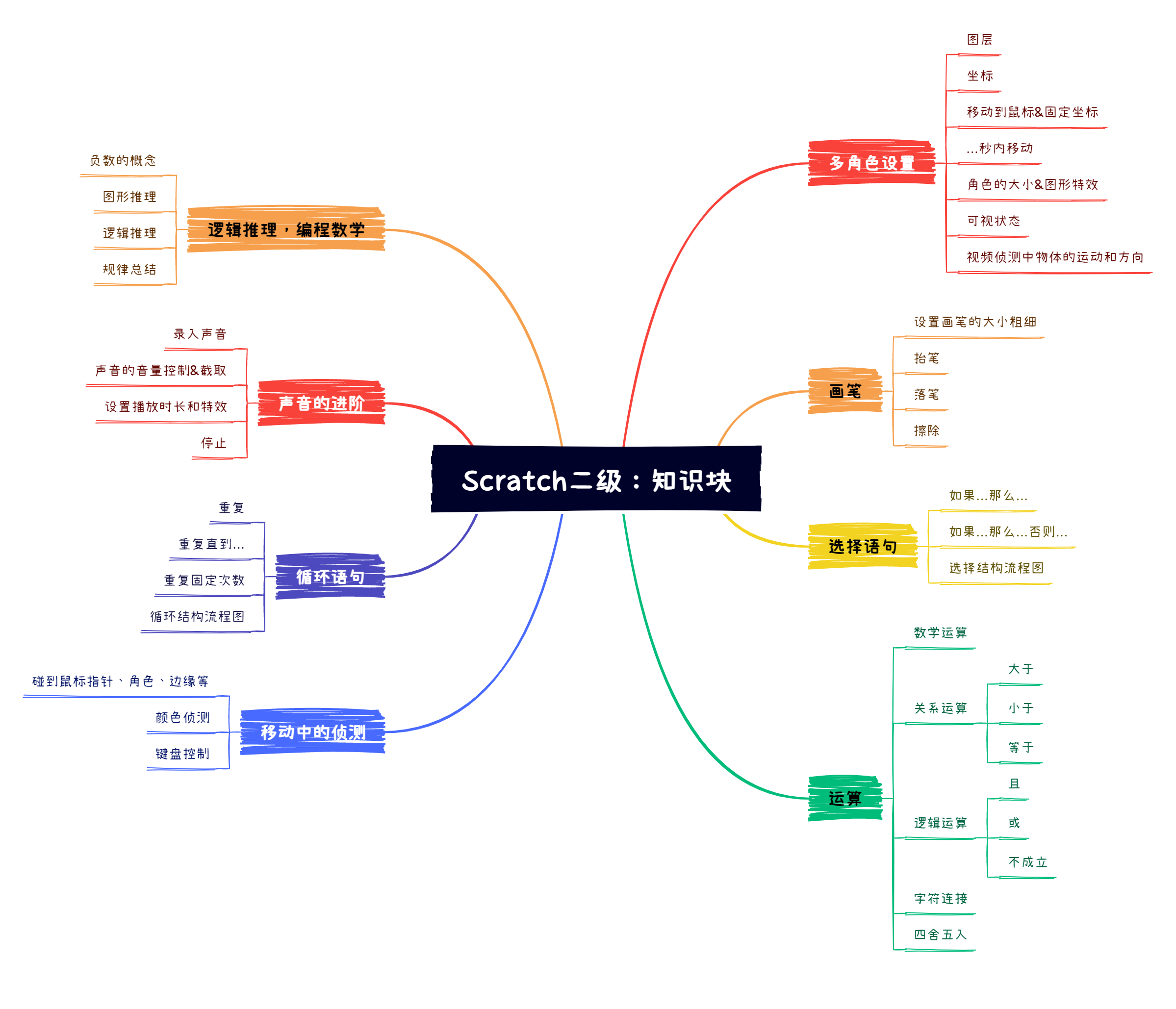
【电子学会】2022年12月图形化二级 -- 老鹰捉小鸡
老鹰捉小鸡 小鸡正在农场上玩耍,突然从远处飞来一只老鹰,小鸡要快速回到鸡舍中,躲避老鹰的抓捕。 1. 准备工作 (1)删除默认白色背景,添加背景Farm; (2)删除默认角色小…...
C++的双端队列
双端队列介绍1.双端队列知识需知2.大试牛刀1.双端队列知识需知 由于队列是一种先进先出(FIFO)的数据结构,因此无法直接从队列的底部删除元素。如果希望从队列的底部删除元素,可以考虑使用双端队列(deque)。…...
)
【独家】华为OD机试 - 拼接 URL(C 语言解题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明本期…...
为什么使用Junit单元测试?Junit的详解
Hi I’m Shendi 为什么使用Junit单元测试?Junit的详解 Junit简介 Junit是一个Java语言的单元测试框架。 单元测试是一个对单一实体(类或方法)的测试 JUnit是由 Erich Gamma 和 Kent Beck 编写的一个回归测试框架(regression test…...

怎么学好嵌入式Linux系统和驱动
嵌入式专业是一门实践性非常强的学科,只有多动手,多实践,多编程,多调试,多看书,多思考才能真正掌握好嵌入式开发技术。 现在很多同学也意识到了学校培养模式和社会需求脱节问题,有一部分同学也先…...

Spring Aware总结
概述 Spring中Aware到底是什么意思? 我们在看Spring源码的时候,经常可以看到xxxAwarexxx的身影,通常我会很疑惑,Aware到底是什么意思呢? 比如图片中这些包含Aware关键字的类或者接口。 我对下面3个类或接口进行了解…...

【RocketMQ】源码详解:Broker端消息刷盘流程
消息刷盘 同步入口:org.apache.rocketmq.store.CommitLog.GroupCommitService 异步入口:org.apache.rocketmq.store.CommitLog.FlushRealTimeService 刷盘有同步和异步两种,在实例化Commitlog的时候,会根据配置创建不同的服务 p…...
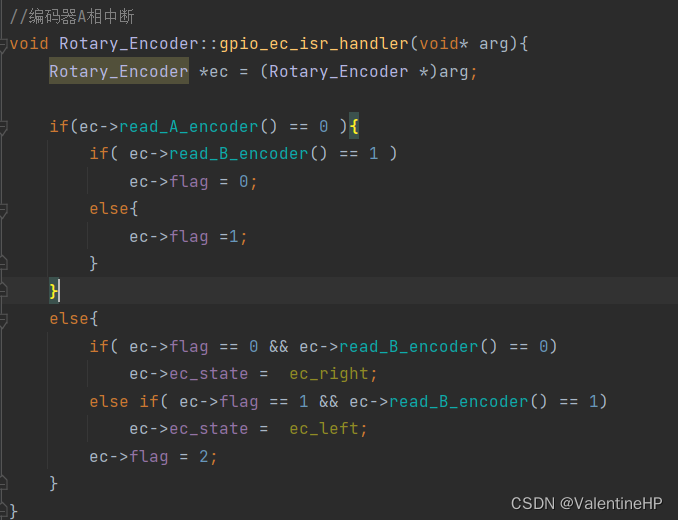
编码器SIQ-02FVS3驱动
一.简介 此编码器可以是功能非常强大,可以检测左右转动,和按键按下,所以说这一个编码器可以抵三个按键,而且体积非常小,使用起来比三个按键要高大尚,而且驱动也简单。唯一不足的点就是价格有点小贵6-8元才…...

【2021.9.7】记一次exe手动添加shellcode
【2021.9.7】记一次exe手动添加shellcode 文章目录【2021.9.7】记一次exe手动添加shellcode0.大致思路1.获取MessageBox的真实地址VA2.通过OD在代码段添加shellcode3.dump出数据,设置程序OEP4.测试dump出来的exe5.方法总结测试的exe和添加了shellcode的exe:链接&…...

常用训练tricks,提升你模型的鲁棒性
目录一、对抗训练FGM(Fast Gradient Method): ICLR2017代码实现二、权值平均1.指数移动平均(Exponential Moving Average,EMA)为什么EMA会有效?代码实现2. 随机权值平均(Stochastic Weight Averaging,SWA&a…...

具有精密内部基准的 DACx0502 简介及驱动应用示例
DACx0502 说明 16 位 DAC80502、14 位 DAC70502 和 12 位DAC60502 (DACx0502) 数模转换器 (DAC) 均为具有电压输出的高精度、低功耗器件。 DACx0502 线性度小于 1LSB。凭借高精度和微型封装特性,DACx0502 非常适合以下 应用: 增益和失调电压校准、电流…...
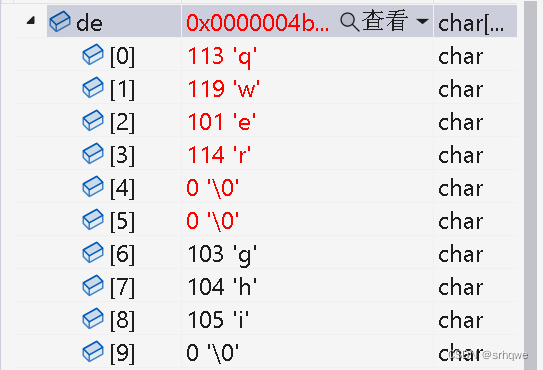
C语言函数:字符串函数及模拟实现strncpy()、strncat()、strncmp()
C语言函数:字符串函数及模拟实现strncpy()、strncat()、strncmp() 在了解strncpy、strncat()、前,需要先了解strcpy()、strncat(): C语言函数:字符串函数及模拟实现strlen() 、strcpy()、 strcat()_srhqwe的博客-CSDN博客 strncp…...

学术论文插图要求简介
1. 类型 位图和矢量图是两种不同的图像类型,它们在存储和处理图像时使用不同的方法。以下是它们之间的详细区别: 图像构成方式:位图使用像素(或图像的最小单元)来构建图像,每个像素都有自己的颜色和亮度值。…...
)
【独家】华为OD机试 - 斗地主 2(C 语言解题)
最近更新的博客 华为od 2023 | 什么是华为od,od 薪资待遇,od机试题清单华为OD机试真题大全,用 Python 解华为机试题 | 机试宝典【华为OD机试】全流程解析+经验分享,题型分享,防作弊指南)华为od机试,独家整理 已参加机试人员的实战技巧文章目录 最近更新的博客使用说明本期…...

力扣-计算特殊奖金
大家好,我是空空star,本篇带大家了解一道简单的力扣sql练习题。 文章目录前言一、题目:1873. 计算特殊奖金二、解题1.正确示范①提交SQL运行结果2.正确示范②提交SQL运行结果3.正确示范③提交SQL运行结果4.正确示范④提交SQL运行结果5.其他总…...

华为校招机试真题目录
专栏介绍 本专栏将逐步收集历年华为校招算法真题 专栏权益 每篇博客都包含: 算法考点解析(文字+画图)算法源码(支持 Java / JS / Python)每晚9:00 ~ 11:00 在线答疑 真题目录 时间题目考点 or 实现2022.11.27...
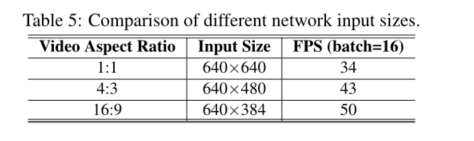
EdgeYOLO学习笔记
EdgeYOLO学习笔记 EdgeYOLO: An Edge-Real-Time Object Detector Abstract 本文基于最先进的YOLO框架,提出了一种高效、低复杂度、无锚的目标检测器,该检测器可以在边缘计算平台上实时实现。为了有效抑制训练过程中的过拟合,我们开发了一种…...

【分布式】什么是分布式锁?正文揭晓
分布式锁的概念 分布式锁其实可以理解为:控制分布式系统有序的去对共享资源进行操作,通过互斥来保持一致性。 举个例子:假设共享的资源就是一个房子,里面有各种书,分布式系统就是要进屋看书的人, 分布式锁…...

synchronized 学习
学习源: https://www.bilibili.com/video/BV1aJ411V763?spm_id_from333.788.videopod.episodes&vd_source32e1c41a9370911ab06d12fbc36c4ebc 1.应用场景 不超卖,也要考虑性能问题(场景) 2.常见面试问题: sync出…...

【杂谈】-递归进化:人工智能的自我改进与监管挑战
递归进化:人工智能的自我改进与监管挑战 文章目录 递归进化:人工智能的自我改进与监管挑战1、自我改进型人工智能的崛起2、人工智能如何挑战人类监管?3、确保人工智能受控的策略4、人类在人工智能发展中的角色5、平衡自主性与控制力6、总结与…...

在rocky linux 9.5上在线安装 docker
前面是指南,后面是日志 sudo dnf config-manager --add-repo https://download.docker.com/linux/centos/docker-ce.repo sudo dnf install docker-ce docker-ce-cli containerd.io -y docker version sudo systemctl start docker sudo systemctl status docker …...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

如何为服务器生成TLS证书
TLS(Transport Layer Security)证书是确保网络通信安全的重要手段,它通过加密技术保护传输的数据不被窃听和篡改。在服务器上配置TLS证书,可以使用户通过HTTPS协议安全地访问您的网站。本文将详细介绍如何在服务器上生成一个TLS证…...

tree 树组件大数据卡顿问题优化
问题背景 项目中有用到树组件用来做文件目录,但是由于这个树组件的节点越来越多,导致页面在滚动这个树组件的时候浏览器就很容易卡死。这种问题基本上都是因为dom节点太多,导致的浏览器卡顿,这里很明显就需要用到虚拟列表的技术&…...

CSS设置元素的宽度根据其内容自动调整
width: fit-content 是 CSS 中的一个属性值,用于设置元素的宽度根据其内容自动调整,确保宽度刚好容纳内容而不会超出。 效果对比 默认情况(width: auto): 块级元素(如 <div>)会占满父容器…...

AI病理诊断七剑下天山,医疗未来触手可及
一、病理诊断困局:刀尖上的医学艺术 1.1 金标准背后的隐痛 病理诊断被誉为"诊断的诊断",医生需通过显微镜观察组织切片,在细胞迷宫中捕捉癌变信号。某省病理质控报告显示,基层医院误诊率达12%-15%,专家会诊…...

安全突围:重塑内生安全体系:齐向东在2025年BCS大会的演讲
文章目录 前言第一部分:体系力量是突围之钥第一重困境是体系思想落地不畅。第二重困境是大小体系融合瓶颈。第三重困境是“小体系”运营梗阻。 第二部分:体系矛盾是突围之障一是数据孤岛的障碍。二是投入不足的障碍。三是新旧兼容难的障碍。 第三部分&am…...

【电力电子】基于STM32F103C8T6单片机双极性SPWM逆变(硬件篇)
本项目是基于 STM32F103C8T6 微控制器的 SPWM(正弦脉宽调制)电源模块,能够生成可调频率和幅值的正弦波交流电源输出。该项目适用于逆变器、UPS电源、变频器等应用场景。 供电电源 输入电压采集 上图为本设计的电源电路,图中 D1 为二极管, 其目的是防止正负极电源反接, …...
