机器视觉【3】非线性求解相机几何参数
线性求解相机几何参数的缺点
上一章节介绍学习了(DLT)线性求解相机几何参数,了解到线性求解法当中比较明显的缺点:
- 没有考虑到镜头畸变的影响
- 不能引入更多的约束条件融入到DLT算法当中优化
- 最关键的是,代数距离并不是计算相机矩阵的最佳距离函数
基于以上问题点,提出非线性求解方法。
- 将包括镜头畸变参数、内外参矩阵等所有信息都当做待求解
- 定义一个比代数距离更好的距离函数
- 通过迭代的非线性最优化算法,最优化上述距离函数,从而得到待求解
在《计算机视觉中的多视角几何》的第7.2节中,用一个插图来说明了线性求解出来的代数距离的几何意义。可以看见,代数距离实际上优化的是已知的3D点X和2D点Xi的反投影点Xi'之间的距离。这并不是一个最优的距离函数。
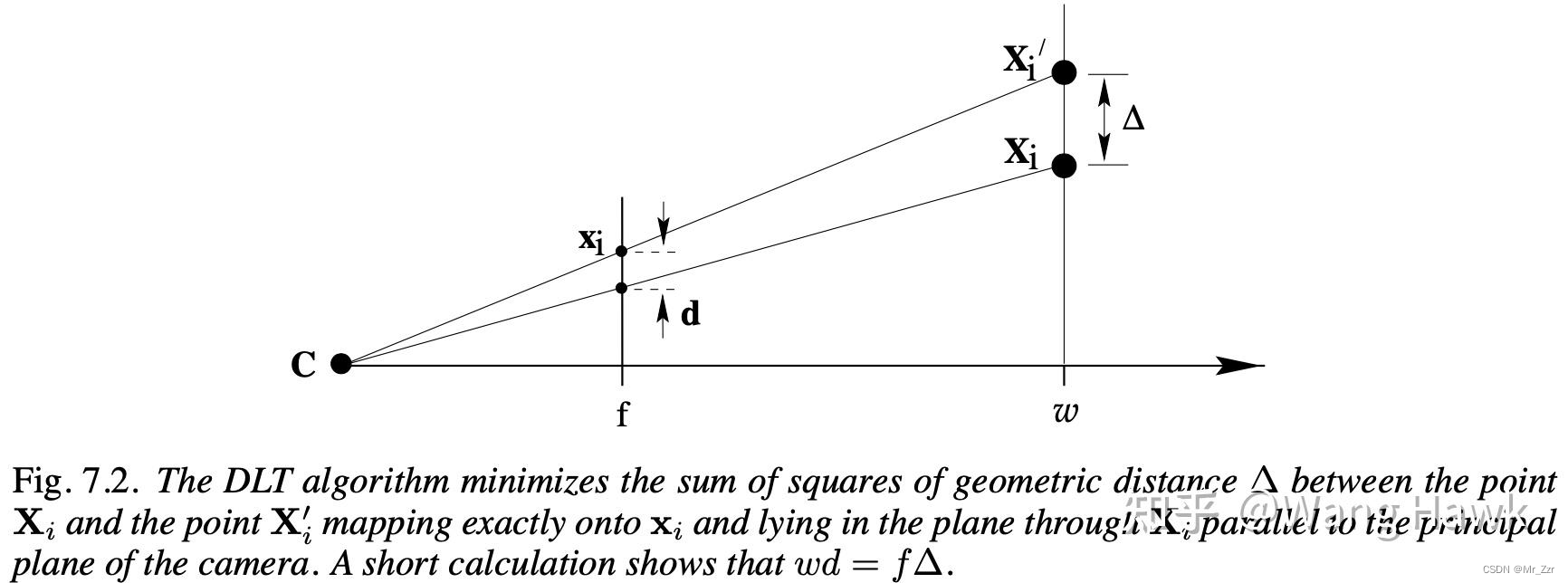
下面我们来看看几何距离,这里假设3D点的位置是准确的(比如我们有一个制作得非常精确的标定板),如下图所示。那么几何距离就是3D点Xi通过投影矩阵投影的2D点xi'和实际成像的2D点xi之间的距离(下图中的红线段)
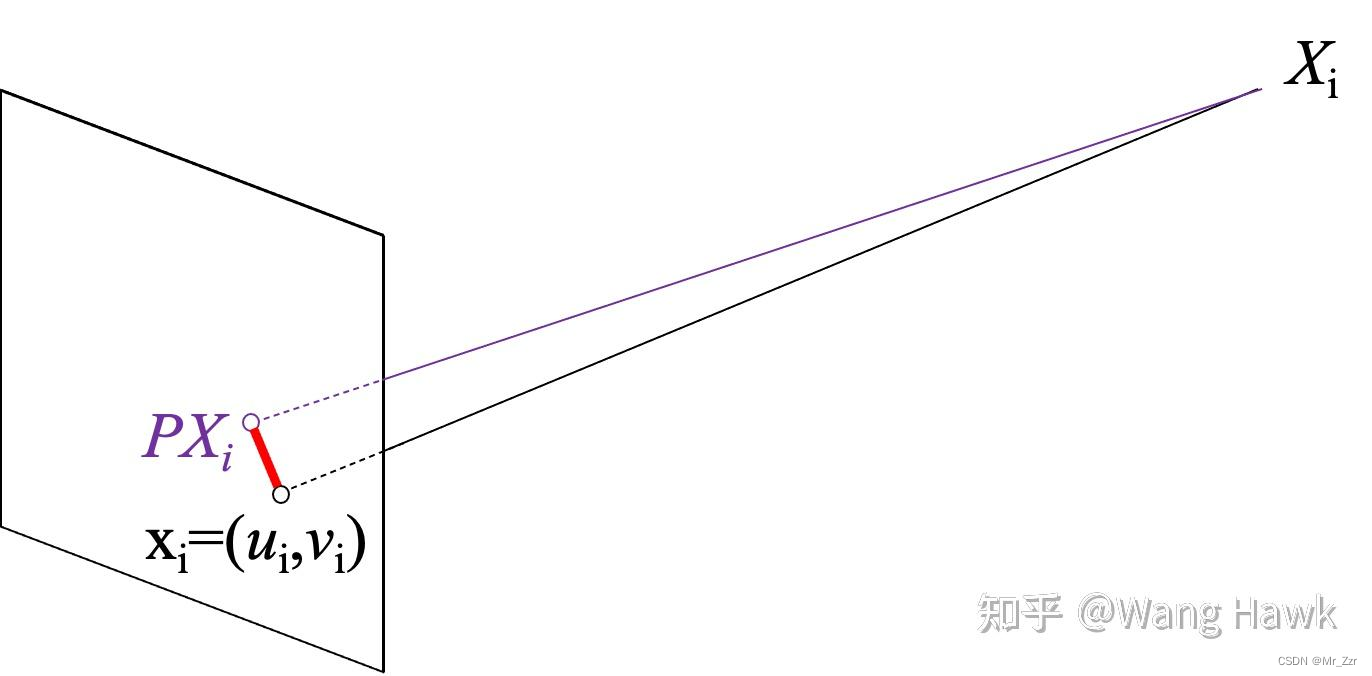
用公式表达式如下所示,整个优化过程就变成了最小化这个距离的过程,如(2)式
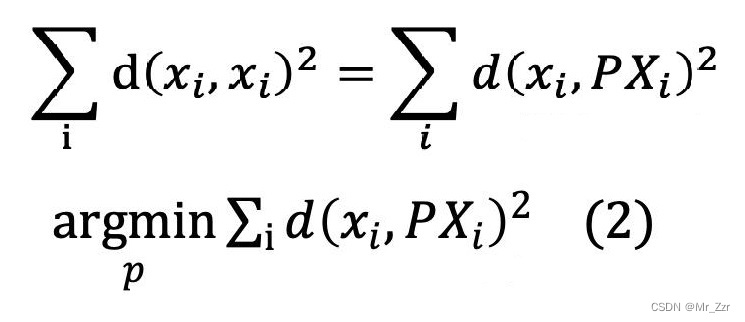
结合之前在 相机的成像(畸变)模型 中的数学模型,式子(2)又可以演变为如下的式子(3)
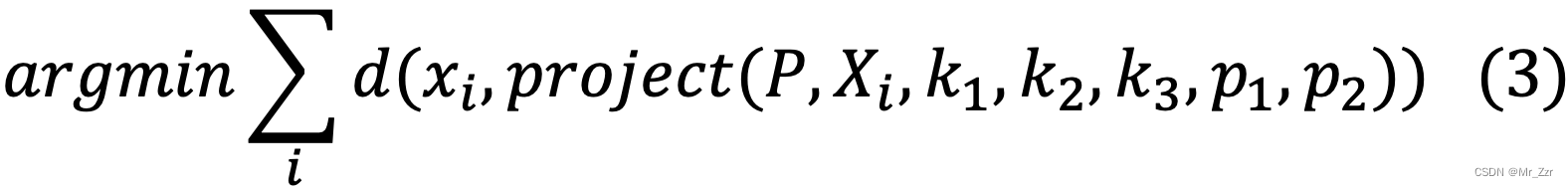
为了执行这个最优化的过程,需要给相机矩阵及畸变参数初始值。其中P的初始值可以用第一节所讲述的DLT算法得到。而畸变参数的初值可以先设置为0。
张正友标定法的实现和完整的过程
在相机几何标定的各种算法中,最出名的无疑是张正友博士发明的“张氏标定法”,这个算法在整个业界得到了广泛的应用,它最大的特点就是灵活、鲁棒、低成本。整个标定过程只需要用相机在不同的方向拍摄平面标定板(最少两次),而它实际上的核心思想就是我上面描述的非线性优化求解方法。
在Matlab和OpenCV中都有张氏标定法的实现,具体使用时先准备好一个足够平整的棋盘格标定板,然后通过不同的方向对标定板进行拍摄,然后进行计算。不需要提前知道相机和标定板之间的具体位姿关系,每次拍摄时的相机和标定板的位姿变换也是独立的,整个使用过程非常友好。

在Matlab中,把上面这些图像输入算法,算法会自动检测出棋盘格角点,并利用前面说的方法优化出各项参数,如果某幅图的平均投影误差超出了用户设置的阈值,还可以方便的过滤掉这幅图来重新进行优化计算。甚至还可以可视化每次拍摄时相机和标定板的位姿,非常方便。
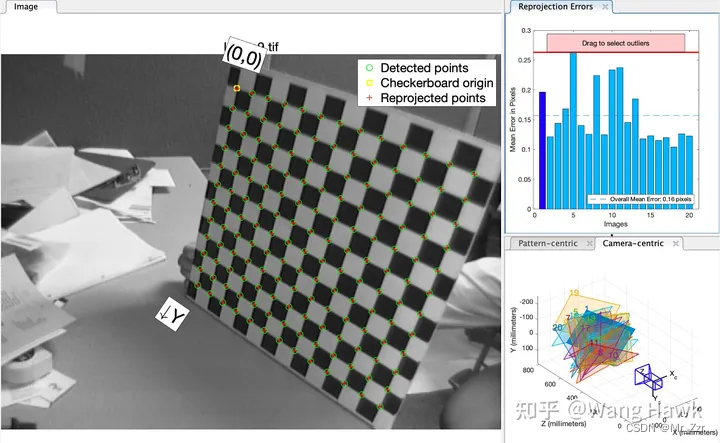
下面简单介绍张正友标定法的关键知识要点。
要点1:引入新的约束条件,从而可以采用平面标定板替代立体标定板
之前讲过标定板需要是立体的,否则无法唯一确定相机矩阵。 然而,立体的标定板是较难去制作的,张氏标定法追求的是低成本的标定方式,因此采用了多次拍摄平面标定板的方式来执行标定。而正因为是多次拍摄,所以每次拍摄时相机矩阵都是变化的,之前讲解的约束条件不再适用:

因此,张氏标定法重新寻求了新的约束条件,用于对内参矩阵进行约束,进而进行求解。作者观察到平面板上的点和对应的像点之间可以用一个单应矩阵H关联在一起,而且只要平面板上的角点足够多(单应矩阵有8个自由度,一对点提供2个约束,所以理论上超过4个即可),就可以求出这个单应矩阵,求解方法类似于上一节所介绍的DLT方法;或者之前学习过的 几何变换模型 中的透视模型,利用最小二乘法求解。
接下重点:作者将单应矩阵表达为H,并观察到内参矩阵K和单应矩阵之间存在着一对约束关系。
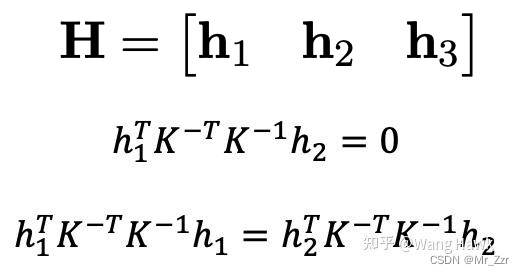
怎么理解上面的两个等式?回想 机器视觉【1】相机的成像(畸变)模型 整合:世界坐标系→像素坐标系的知识点
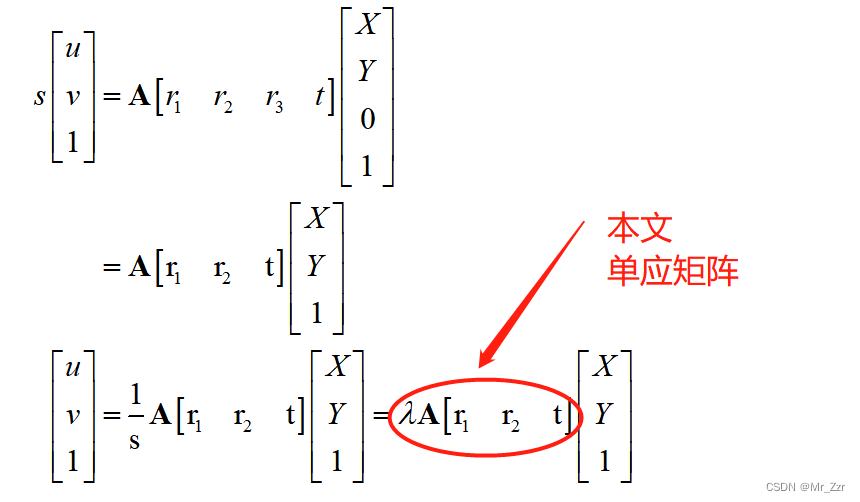
这里的λ只是1/s的另一种表示,只是换了一种写法
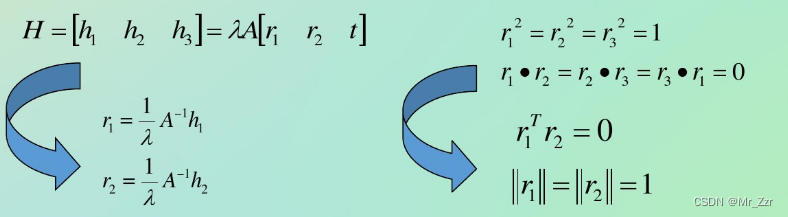
这里有人会不理解,r1=和r2=是怎么来的?其实自己可以推导一下,把A设成[3X3]的矩阵,乘进去,应该能够看到,组成了[Ar1 Ar2 Ar3],它们互相还是独立的。至于为什么A到A逆,这个是线性代数最基本的转换,左右同时左乘A逆,就变过来了。
这里的A其实就是内参矩阵K,上面两个式子其实不难证明 (以下 A' 为 矩阵A的逆 即上图示的A-1)
由前置知识:A'H = A' · λ · A · [r1 r2 t] = [r1 r2 t],λ是常数可暂时忽略
根据线性代数基本规律:(AB)T = BT · AT 即 矩阵A和B相乘之后的转置等于B的转置乘A的转置
那么:(h1)T * (A)−T * (A)−1 * h2 = r1T * r2 = 0
第一个公式证得r1和r2是正交的关系。
对第二个式子左右两边进行上述变换,得 r1T * r1 = r2T * r2,由此可知 r1和r2是单位正交。
最后,我们把上述的两个式子中间 (K)-T*(K)-1的部分记作B,其余h部分利用线性基础变换写出另外一部分。即如下表示
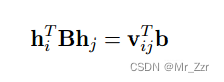
这样,我们又可以用SVD奇异值分解的方式,求得b,进而求得K的各个元素。当求得了K之后,就很容易得到这一次拍摄时的外参信息(旋转R和平移t)了。上面讲的方法用于初始化内参矩阵K和每次拍摄的外参R和t,我们假设一共进行n次拍摄,每次拍摄可以获得m个成像点,那么就可以利用非线性最优化方法,来最优化待解参数了。具体表达式如下:
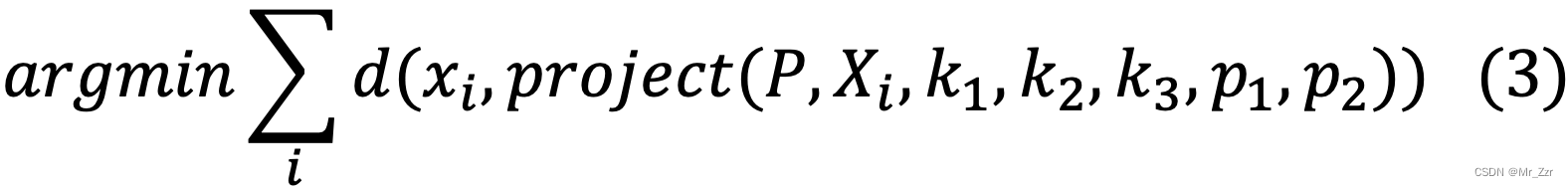
要点2:在多次拍摄时,需要改变标定板的方向
在张博士的论文中详述了如果两次拍摄时的标定板是平行的,那么实际上并没有提供额外的信息,也因此无法求解出需要的参数。
要点3:最少需要拍摄几幅图?
前面讲到,每一幅拍摄的标定板图像提供了2个对内参矩阵K的约束,而我们内参矩阵K一共有5个未知参数,所以理论上至少需要拍摄3幅图像,才能求得K:

如果我们认为s=0,即传感器像素是规整方形的,那么内参矩阵就只有4个未知参数了,这样就只需要拍摄两幅图像就能进行标定了。
前面讲过,这样的约束关系是为了求得比较好初始化内参矩阵K的。如果你能够事先知道K中元素的大概值,比如你认为s=0, 主点位于图像的中心, 而焦距又是已知的,那么理论上你只需要拍摄一幅平面的标定板一次,就可以通过非线性最小二乘法标定出相机的内外参数。
Reference:
张正友相机标定全解析_定焦相机张正友标定法怎么用-CSDN博客
相机标定(具体过程详解)张正友、单应矩阵、B、R、T_已知内参数下标定r、t-CSDN博客
总结
前文和本文中讲解了相机标定的两大类方法:线性求解方法,以及非线性求解方法。
不管是哪种方法,我都提到了数据归一化的重要性,因为在求解过程中的矩阵元素如果不经过归一化,值差异较大,很容易放大数值误差,需要特别注意这点。经过相机的标定,我们就可以获得了包括畸变参数在内的相机内参,以及每次拍摄时的外参。
博主我的自述:
说实话,之前是知道这一块比较复杂,但没想过是这么复杂。现实接触的情况都是用现成的库或者软件工具一键处理,这次花力气去理解算是 "拨开云雾见天日,守得云开见月明",新的一年祝大家工作顺利,万事如意,大家加油!
相关文章:

机器视觉【3】非线性求解相机几何参数
线性求解相机几何参数的缺点 上一章节介绍学习了(DLT)线性求解相机几何参数,了解到线性求解法当中比较明显的缺点: 没有考虑到镜头畸变的影响不能引入更多的约束条件融入到DLT算法当中优化最关键的是,代数距离并不是…...
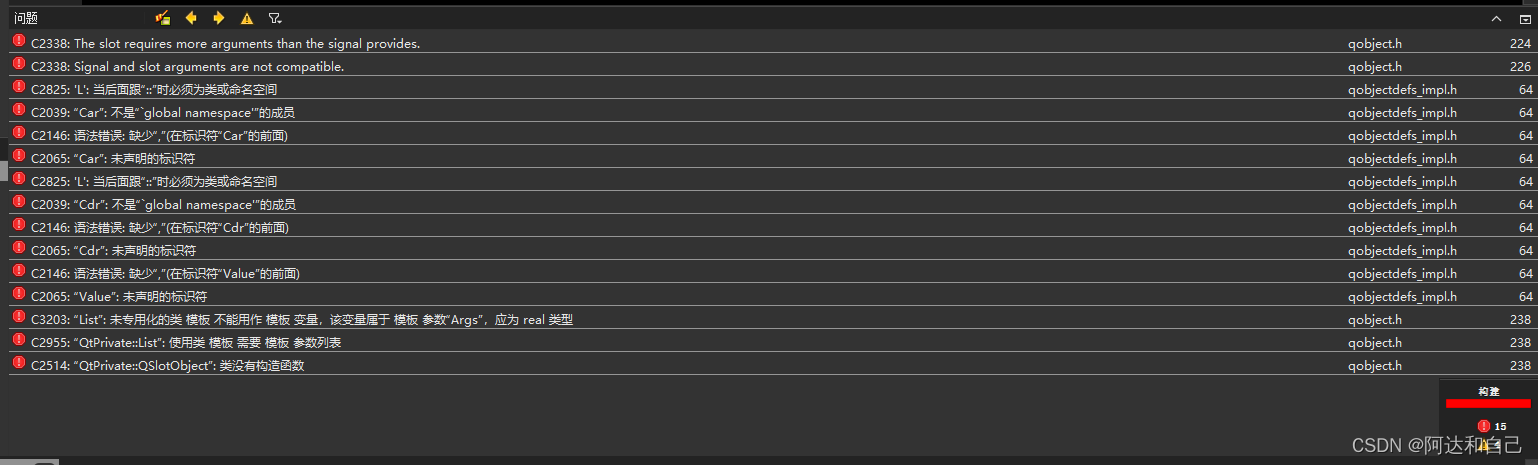
Qt编译报错:The slot requires more arguments than the signal provides.
编译时代码没有提示错误的地方,报错的地方在qt的文件,还以为什么莫名其妙的错误呢,原来就是连接的信号和槽函数参数不匹配,有个信号是没有参数的,但我的槽函数有个参数,然后就报错了。 改下槽函数的参数就…...
【Unity】提示No valid Unity Editor liscense found.Please active your liscense.
有两个软件,如果只有一个,点黑的不会有效果、、、、(楼主是这个原因,可以对号入座一下) 简而言之,就是去下载Unity Hub,再里面激活管理通行证 问题情境: 点击unity出现以下弹窗&a…...
如何在 Tomcat 中为 Web 应用程序启用和配置缓存?
在Tomcat中为Web应用程序启用和配置缓存通常涉及到对Tomcat的连接器(Connector)进行配置,以及可能的话,配置Web应用程序本身以支持缓存。 1. 配置Tomcat连接器以启用缓存 Tomcat的连接器可以通过其配置来启用各种…...

QEMU开发入门
1. 简介 QEMU(Quick EMUlator)是一个开源的虚拟化软件,它能够模拟多种硬件平台,并在这些平台上运行各种操作系统。QEMU可以在不同的主机架构之间进行虚拟化,例如x86、ARM、PowerPC、Risc-V等。QEMU是一个功能强大且灵…...
10-pytorch-完整模型训练
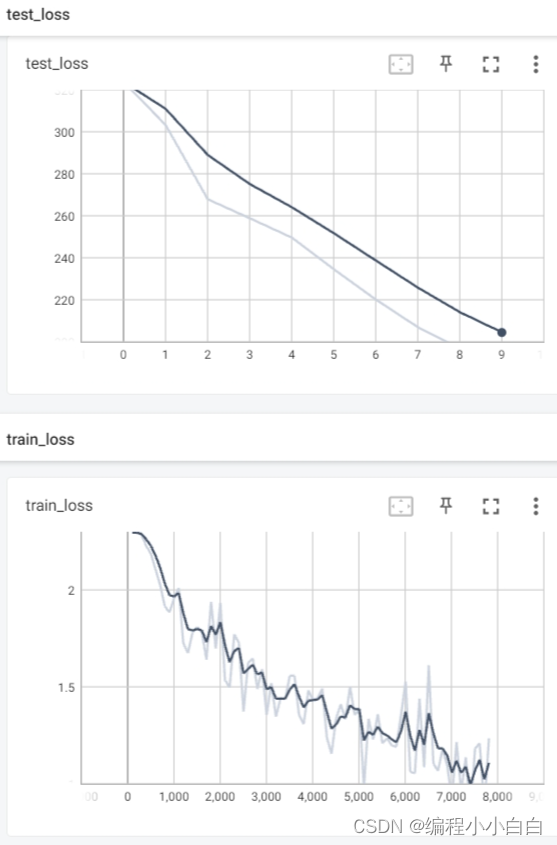
b站小土堆pytorch教程学习笔记 一、从零开始构建自己的神经网络 1.模型构建 #准备数据集 import torch import torchvision from torch.utils.tensorboard import SummaryWriterfrom model import * from torch.utils.data import DataLoadertrain_datatorchvision.datasets.…...
高级RAG:重新排名,从原理到实现的两种主流方法
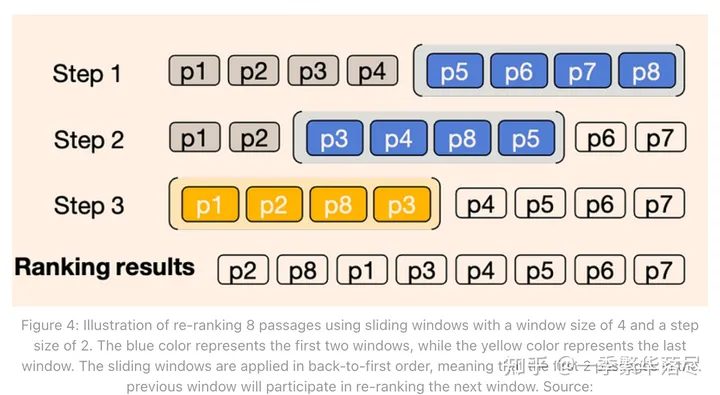
原文地址:https://pub.towardsai.net/advanced-rag-04-re-ranking-85f6ae8170b1 2024 年 2 月 14 日 重新排序在检索增强生成(RAG)过程中起着至关重要的作用。在简单的 RAG 方法中,可以检索大量上下文,但并非所有上下…...
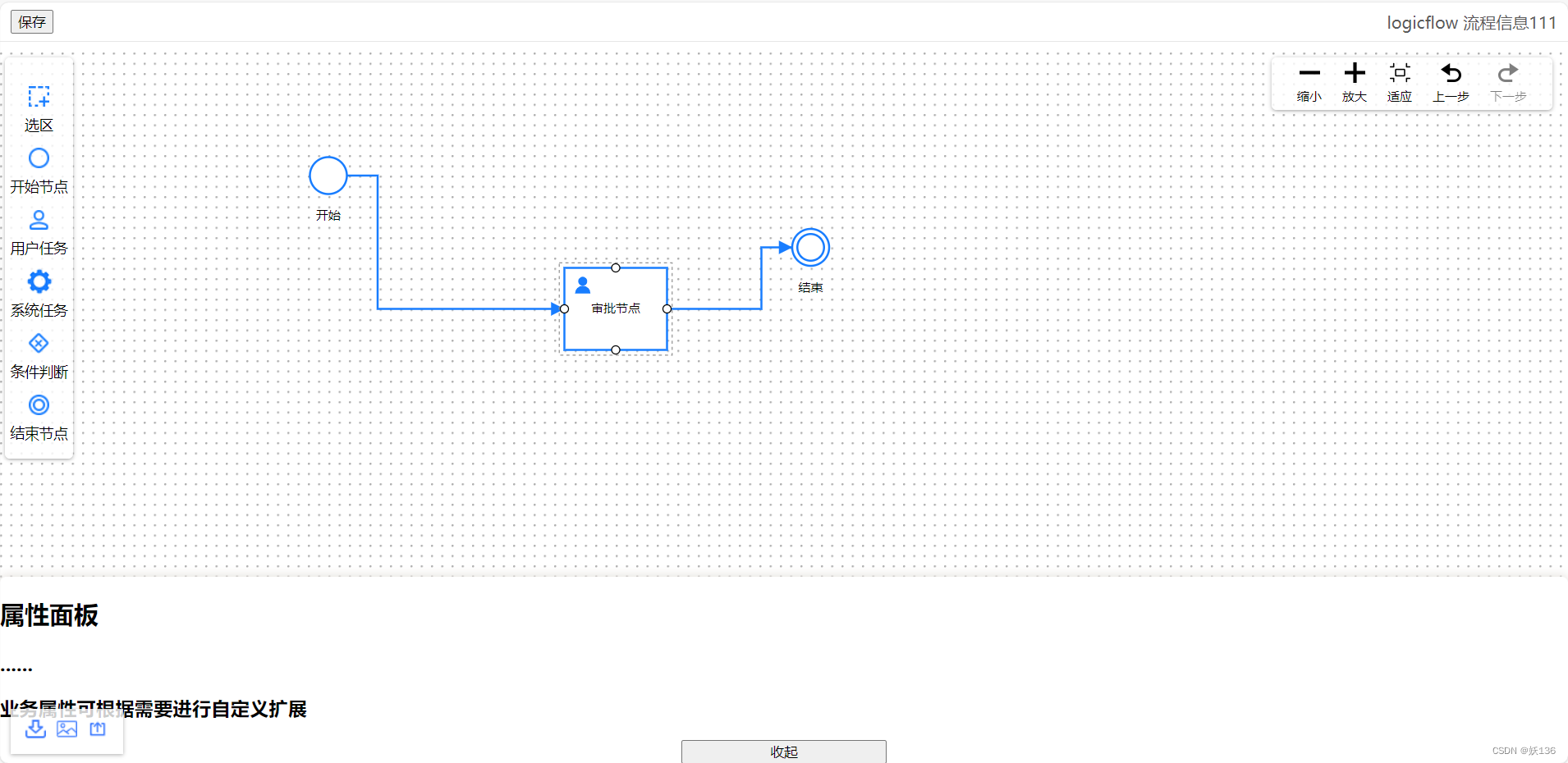
使用logicflow流程图实例
一.背景 需要使用流程引擎开发项目,没有使用flowable、activiti这类的国外流程引擎,想使用国内的引擎二次开发,缺少单例模式的流程画图程序,都是vue、react、angluer的不适合,从网上找了antx6、logicflow、bpmn.js。感…...

Stable Diffusion 绘画入门教程(webui)-ControlNet(IP2P)
上篇文章介绍了深度Depth,这篇文章介绍下IP2P(InstructP2P), 通俗理解就是图生图,给原有图加一些效果,比如下图,左边为原图,右边为增加了效果的图: 文章目录 一、选大模型二、写提示词三、基础参…...
)
五力分析(Porter‘s Five Forces)
五力分析是一种用于评估竞争力的框架,由哈佛商学院教授迈克尔波特(Michael Porter)提出。它通过分析一个行业的五个关键力量(竞争对手、供应商、顾客、替代品和新进入者)来评估一个企业或行业的竞争环境。这个框架可以…...
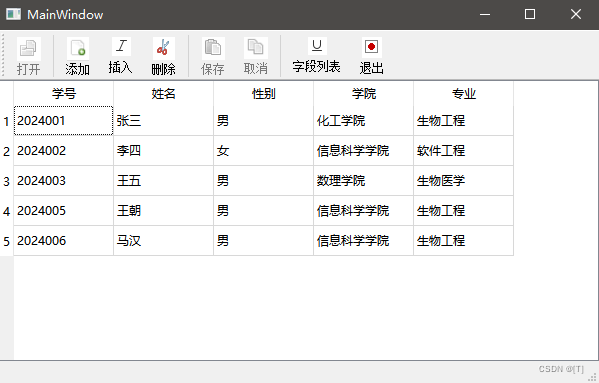
十一、Qt数据库操作
一、Sql介绍 Qt Sql模块包含多个类,实现数据库的连接,Sql语句的执行,数据获取与界面显示,数据与界面直接使用Model/View结构。1、使用Sql模块 (1)工程加入 QT sql(2)添加头文件 …...
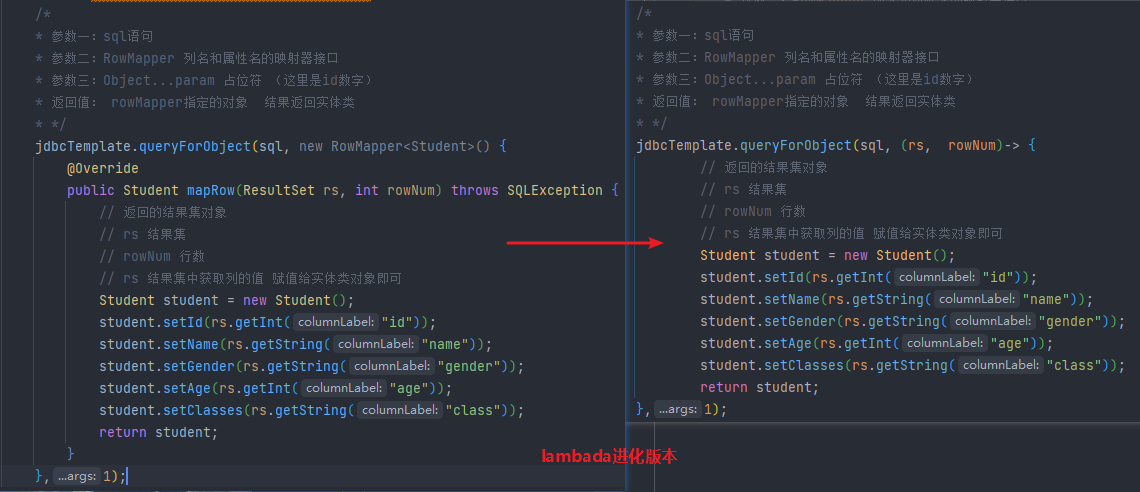
【Spring】IoC容器 控制反转 与 DI依赖注入 XML实现版本 第二期
文章目录 基于 XML 配置方式组件管理前置 准备项目一、 组件(Bean)信息声明配置(IoC):1.1 基于无参构造1.2 基于静态 工厂方法实例化1.3 基于非静态 工厂方法实例化 二、 组件(Bean)依赖注入配置…...
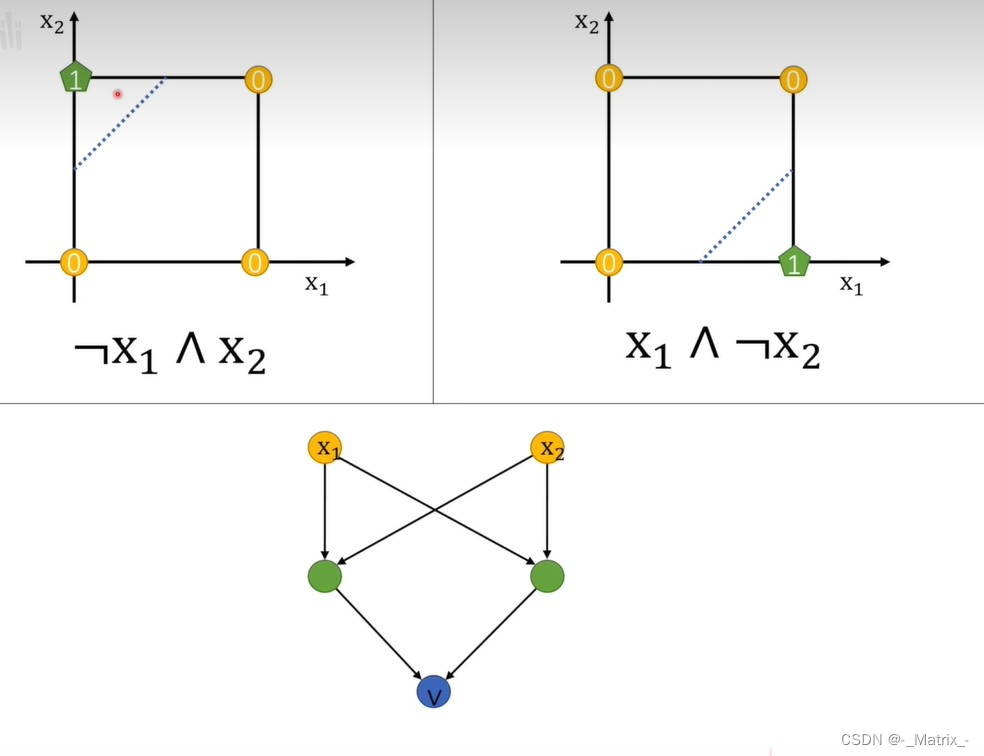
神经网络系列---感知机(Neuron)
文章目录 感知机(Neuron)感知机(Neuron)的决策函数可以表示为:感知机(Neuron)的学习算法主要包括以下步骤:感知机可以实现逻辑运算中的AND、OR、NOT和异或(XOR)运算。 感知机(Neuron) 感知机(Neuron)是一种简单而有效的二分类算法,用于将输入…...

k8s(2)
目录 一.二进制部署k8s 常见的K8S安装部署方式: k8s部署 二进制与高可用的区别 二.部署k8s 初始化操作: 每台node安装docker: 在 master01 节点上操作; 准备cfssl证书生成工具:: 执行脚本文件: 拉入etcd压缩包…...
利用nginx内部访问特性实现静态资源授权访问
在nginx中,将静态资源设为internal;然后将前端的静态资源地址改为指向后端,在后端的响应头部中写上静态资源地址。 近期客户对我们项目做安全性测评,暴露出一些安全性问题,其中一个是有些静态页面(*.html&…...
fly-barrage 前端弹幕库(1):项目介绍
fly-barrage 是我写的一个前端弹幕库,由于经常在 Bilibili 上看视频,所以对网页的弹幕功能一直蛮感兴趣的,所以做了这个库,可以帮助前端快速的实现弹幕功能。 项目官网地址:https://fly-barrage.netlify.app/ÿ…...

jetcache如果一个主体涉及多个缓存时编辑或者删除时如何同时失效多个缓存
在实际使用过程中,可能会遇到这种情形:一个主体会有多个缓存,比如用户基础信息缓存、用户详情缓存,那么当删除用户信息后就需要同时失效多个缓存中该主体数据,那么jetcache支持这种应用场景么,答案是支持&a…...

uni-app 实现拍照后给照片加水印功能
遇到个需求需要实现,研究了一下后写了个demo 本质上就是把拍完照后的照片放到canvas里,然后加上水印样式然后再重新生成一张图片 代码如下,看注释即可~使用的话记得还是得优化下代码 <template><view class"content"&g…...

【ArcGIS】利用DEM进行水文分析:流向/流量等
利用DEM进行水文分析 ArcGIS实例参考 水文分析通过建立地表水文模型,研究与地表水流相关的各种自然现象,在城市和区域规划、农业及森林、交通道路等许多领域具有广泛的应用。 ArcGIS实例 某流域30m分辨率DEM如下: (1)…...

论文阅读笔记——PathAFL:Path-Coverage Assisted Fuzzing
文章目录 前言PathAFL:Path-Coverage Assisted Fuzzing1、解决的问题和目标2、技术路线2.1、如何识别 h − p a t h h-path h−path?2.2、如何减少 h − p a t h h-path h−path的数量?2.3、哪些h-path将被添加到种子队列?2.4、种…...

C++实现分布式网络通信框架RPC(3)--rpc调用端
目录 一、前言 二、UserServiceRpc_Stub 三、 CallMethod方法的重写 头文件 实现 四、rpc调用端的调用 实现 五、 google::protobuf::RpcController *controller 头文件 实现 六、总结 一、前言 在前边的文章中,我们已经大致实现了rpc服务端的各项功能代…...

《基于Apache Flink的流处理》笔记
思维导图 1-3 章 4-7章 8-11 章 参考资料 源码: https://github.com/streaming-with-flink 博客 https://flink.apache.org/bloghttps://www.ververica.com/blog 聚会及会议 https://flink-forward.orghttps://www.meetup.com/topics/apache-flink https://n…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

网络编程(UDP编程)
思维导图 UDP基础编程(单播) 1.流程图 服务器:短信的接收方 创建套接字 (socket)-----------------------------------------》有手机指定网络信息-----------------------------------------------》有号码绑定套接字 (bind)--------------…...

如何在网页里填写 PDF 表格?
有时候,你可能希望用户能在你的网站上填写 PDF 表单。然而,这件事并不简单,因为 PDF 并不是一种原生的网页格式。虽然浏览器可以显示 PDF 文件,但原生并不支持编辑或填写它们。更糟的是,如果你想收集表单数据ÿ…...
)
Angular微前端架构:Module Federation + ngx-build-plus (Webpack)
以下是一个完整的 Angular 微前端示例,其中使用的是 Module Federation 和 npx-build-plus 实现了主应用(Shell)与子应用(Remote)的集成。 🛠️ 项目结构 angular-mf/ ├── shell-app/ # 主应用&…...
实现跳一跳小游戏)
鸿蒙(HarmonyOS5)实现跳一跳小游戏
下面我将介绍如何使用鸿蒙的ArkUI框架,实现一个简单的跳一跳小游戏。 1. 项目结构 src/main/ets/ ├── MainAbility │ ├── pages │ │ ├── Index.ets // 主页面 │ │ └── GamePage.ets // 游戏页面 │ └── model │ …...

数据结构:泰勒展开式:霍纳法则(Horner‘s Rule)
目录 🔍 若用递归计算每一项,会发生什么? Horners Rule(霍纳法则) 第一步:我们从最原始的泰勒公式出发 第二步:从形式上重新观察展开式 🌟 第三步:引出霍纳法则&…...

CMS内容管理系统的设计与实现:多站点模式的实现
在一套内容管理系统中,其实有很多站点,比如企业门户网站,产品手册,知识帮助手册等,因此会需要多个站点,甚至PC、mobile、ipad各有一个站点。 每个站点关联的有站点所在目录及所属的域名。 一、站点表设计…...

使用homeassistant 插件将tasmota 接入到米家
我写一个一个 将本地tasmoat的的设备同通过ha集成到小爱同学的功能,利用了巴法接入小爱的功能,将本地mqtt转发给巴法以实现小爱控制的功能,前提条件。1需要tasmota 设备, 2.在本地搭建了mqtt服务可, 3.搭建了ha 4.在h…...
