欧几里得和《几何原本》
欧几里得和《几何原本》
欧几里得(Euclid),公元前约300年生于古希腊,被认为是几何学的奠基人之一。他的主要成就是编写了一本名为《几何原本》(Elements)的著作,这本书成为了几何学的经典教材,并且在整个古代和中世纪都广泛使用。
《几何原本》是一本包含了几何学基本原理、定理和证明的书籍,被分为13个卷,涵盖了平面几何、立体几何、数论等不同领域。第 1~4 卷主要为平面几何, 但间杂了数的理论——比如第 2 卷给出了乘法对加法的分配律等, 并求解了若干代数方程; 第 5~6 卷为比例理论及相似理论, 但同样间杂了数的理论, 且其中第 5 卷关于数有很深刻的洞见; 第 7~9 卷以对数学分支的现代分类观之, 是对几何与数的相对比例的的逆转——转入了以数为主的数论范畴, 其中包括了对 “素数有无穷多个” (第 9 卷命题 20) 等重要命题的证明; 第 10 卷对 “不可公度量” (incommensurable)——也就是无理数——做了详细讨论; 第 11~13 卷对包括 “柏拉图正多面体” (Plato solid) 在内的诸多立体几何话题的探讨。欧几里得在书中使用了严格的演绎推理和逻辑,建立了一个完整的几何体系,并以此为基础,推导出了许多重要的几何定理,如直角三角形的勾股定理等。
欧几里得的《几何原本》对后世的数学发展影响深远。它不仅在古代和中世纪被广泛教授和学习,而且在现代数学中仍然具有重要地位。这本书的几何思想和证明方法影响了许多后来的数学家,包括笛卡尔和牛顿等。欧几里得的贡献被认为是几何学的里程碑,也为后来的数学研究奠定了基础。
在《几何原本》中,欧几里得从一些基本的几何概念和公理出发,逐步推导出各种几何定理,构建了一个完善的几何体系。这个体系不仅包括了平面几何和立体几何的知识,还涉及了数论和几何代数等领域。通过逻辑推理和演绎方法,欧几里得展示了几何学的严密性和逻辑性,使得《几何原本》成为了几何学的经典教材,被广泛传颂和学习。
《几何原本》,是古希腊数学家欧几里得(Euclid)所著的一部数学著作,完成于公元前300年左右。这部著作是一本系统介绍几何学和数学原理的书籍,对后世的数学、科学乃至哲学产生了深远的影响。
中文书名由来
1577 年意大利人利玛窦获准赴遥远的东方传教,1582年利玛窦来到了澳门,1598年他到了南京。 两年后(1600年),一位从上海进京赶考的读书人在南京拜访了利玛窦。他们交谈十分投机,这位读书人便是徐光启。1604年, 四十三岁的徐光启第三次参加会试终于考取了进士,成为翰林院庶吉士。而此时利玛窦也终于获明神宗同意在北京定居传教。从1606年秋天开始,每天安排固定的三、四个小时功课。先由利玛窦口头翻译并讲解,再由徐光启草录,两人再反复推敲验证,之后再由徐光启撰写成典雅的中文。【利玛窦和徐光启翻译的底本是利玛窦在罗马学院的数学老师克拉乌(Christoph Clavius)审订和注释的拉丁文版《欧几里得的基本原理》(Euclidis Elementorum)。欧几里德的著作Στοιχεα本来只有十三卷,克拉乌在后面又增添了两卷注释,这样总共十五卷。】
《几何原本》希腊文的名称Στοιχεα,意思是“原理”,英文书名the Elements,自拉丁文的Elementa,元素。利玛窦徐光启就把拉丁文Elementa翻译为“原本”,意为本原,原始,将中文书名确定为《几何原本》。 “平行线”、“三角形”、“对角”、“直角”、“锐角”、“钝角”、“相似” 这些我们如今已耳熟能详的术语,也都是利玛窦与徐光启反复推敲确定下来的。
顺便说明,1610年,58岁的利玛窦病逝。《几何原本》后9卷的翻译在利玛窦逝世后便搁置了。这一搁就是250年。直到1857年才由清朝数学家李善兰(1811-1882年)与英国伦敦会传教士伟烈亚力(Alexander Wylie, 1815-1887年)共同翻译完成。
《几何原本》13卷,有人做了较详细的统计:
第1卷由23条定义、5条公设、5条公理以及48个命题组成,全部讲解平面几何知识。其中命题47对勾股定理进行了证明,该命题也是本卷最重要的一条命题。第2卷由2条定义、14个命题组成,主要讲解的代数恒等式。第3卷由11条定义、37个命题组成,第4卷由5条定义、16个命题组成。第3卷、第4卷全部讲解圆的知识。第5卷由18条定义、25个命题组成,主要探讨比例。希思认为,希腊数学中没有什么发现比本卷中的理论更能令人夸耀。霍金《上帝创造整数》一书追溯了数学史上2500年间17位数学家31篇著作,该书对本卷全部25个命题进行了详细的讲解,而第1卷中仅有命题47勾股定理被收录了。可见本卷内容价值很高。第6卷由3条定义、33个命题,主要讲解相似图形。第7卷由22条定义、39个命题组成,主要讲解初等数论。霍金在《上帝创造整数》一书中,对本卷全部39个命题进行了详细的讲解。第8卷由26个命题组成。第7卷、第8卷对奇数、偶数、平方数等进行了定义,主要讲解了素数。第9卷由36个命题组成。本卷对有理数、无理数进行了深入的讲解。第10卷由4个定义、115个命题组成。本卷是全书命题数最多的一卷,主要讲解不可公度量。第11卷由28个定义、39个命题组成。第12卷由18个命题组成。第13卷由18个命题组成。这3卷全部讨论的立体几何学知识,并在一些命题证明中使用了穷竭法。
参考:
中意交往史上的琴箫合奏——利玛窦徐光启合译《几何原本》 (qq.com)
相关文章:

欧几里得和《几何原本》
欧几里得和《几何原本》 欧几里得(Euclid),公元前约300年生于古希腊,被认为是几何学的奠基人之一。他的主要成就是编写了一本名为《几何原本》(Elements)的著作,这本书成为了几何学的经典教材&a…...

linux c++ 开发 tensorrt 安装
tensorrt 官方下载地址(需要注册账号登录):Log in | NVIDIA Developer 根据系统发行版和CUDA版本 (nvcc -V) 选择合适的安装包 EA(early access)版本代表抢先体验。 GA(general availability)代…...
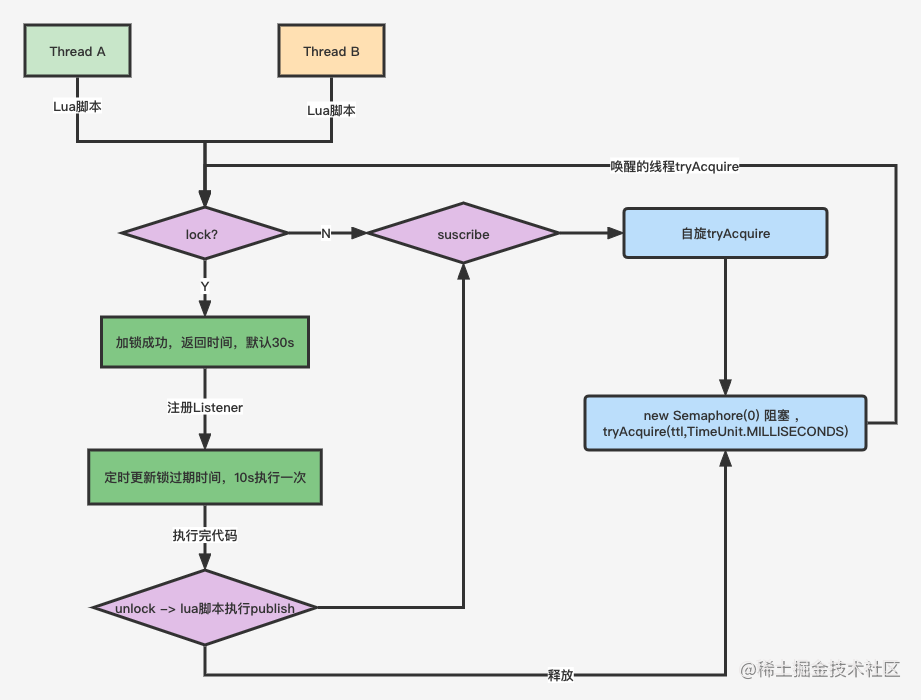
Redis高并发分布锁实战
Redis高并发分布锁实战 问题场景 场景一: 没有捕获异常 // 仅仅加锁 // 读取 stock15 Boolean ret stringRedisTemplate.opsForValue().setIfAbsent("lock_key", "1"); // jedis.setnx(k,v) // TODO 业务代码 stock-- stringRedisTemplate.delete(&quo…...

Kotlin基础——DSL
DSL(领域特定语言) 常见的DSL就是SQL和正则表达式,用于操作数据库和文本字符串,Kotlin DSL通常为嵌套的Lambda表达式或链式方法,如 https://github.com/gradle/gradle-script-kotlin 用于构建Gradle脚本https://gith…...

《Docker 简易速速上手小册》第4章 Docker 容器管理(2024 最新版)
文章目录 4.1 容器生命周期管理4.1.1 重点基础知识4.1.2 重点案例:启动并管理 Python Flask 应用容器4.1.3 拓展案例 1:调试运行中的容器4.1.4 拓展案例 2:优雅地停止和清理容器 4.2 容器数据管理与持久化4.2.1 重点基础知识4.2.2 重点案例&a…...
【人脸朝向识别与分类预测】基于PNN神经网络
课题名称:基于PNN神经网络的人脸朝向识别分类 版本日期:2024-02-20 运行方式:直接运行PNN0503.m文件 代码获取方式:私信博主或 QQ:491052175 模型描述: 采集到一组人脸朝向不同角度时的图像,图像来自不…...
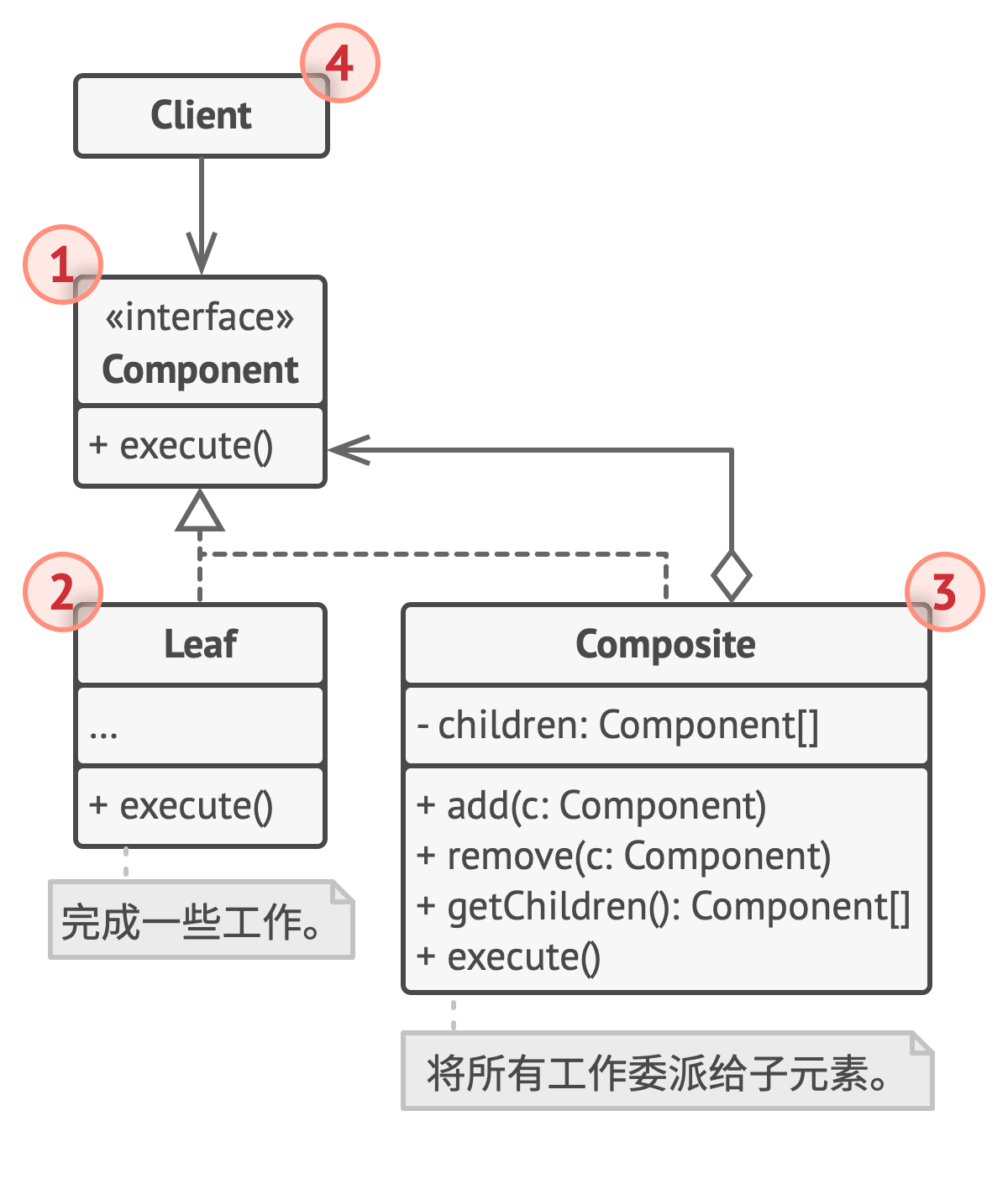
【Python笔记-设计模式】组合模式
一、说明 组合模式是一种结构型设计模式, 你可以使用它将对象组合成树状结构, 并且能像使用独立对象一样使用它们。 (一) 解决问题 处理树形结构:可以很好地处理树形结构的数据,使得用户可以统一对待单个对象和对象组合。统一接…...

51单片机学习(5)-----蜂鸣器的介绍与使用
前言:感谢您的关注哦,我会持续更新编程相关知识,愿您在这里有所收获。如果有任何问题,欢迎沟通交流!期待与您在学习编程的道路上共同进步。 目录 一. 蜂鸣器的介绍 1.蜂鸣器介绍 2.压电式蜂鸣器 (无源…...

-bash: /root/.ssh/authorized_keys: Read-only file system
问题背景 由于跳板机不支持 ssh-copy-id 命令,为了配置免密登录,考虑在服务器上手动使用 cat 命令写入跳板机公钥 cat <<EOL >> ~/.ssh/authorized_keys [Your public key] EOL但却出现了以下错误 -bash: /root/.ssh/authorized_keys: Re…...
3,设备无关位图显示
建立了一个类Dib Dib.h #pragma once #include “afx.h” class CDib :public CObject { public: CDib(); ~CDib(); char* GetFileName(); BOOL IsValid(); DWORD GetSize(); UINT GetWidth(); UINT GetHeight(); UINT GetNumberOfColors(); RGBQUAD* GetRGB(); BYTE* GetDat…...

转前端了!!
大家好,我是冰河~~ 没错,为了更好的设计和开发分布式IM即时通讯系统,也为了让大家能够直观的体验到分布式IM即时通讯系统的功能,冰河开始转战前端了。也就是说,整个项目从需求立项到产品设计,从架构设计到…...

RESTful API如何使用它构建 web 应用程序。
链接:华为机考原题 RESTful API(Representational State Transfer)是一种基于网络的软件架构风格,用于设计和访问网络资源。它是一种轻量级、灵活、可扩展的架构,常用于构建Web应用程序和服务。 使用RESTful API构建Web应用程序的步骤如下&…...

现在学Oracle是49年入国军么?
今天周末,不聊技术,聊聊大家说的最多的一个话题 先说明一下,防止挨喷😆 本人并不是职业dba,对数据库就是爱好,偶尔兼职,以下仅个人观点分析,如有不同观点请轻喷,哈哈&…...

【回溯】组合问题||
给定一个候选人编号的集合 candidates 和一个目标数 target ,找出 candidates 中所有可以使数字和为 target 的组合。 candidates 中的每个数字在每个组合中只能使用 一次 。 注意:解集不能包含重复的组合。 示例 1: 输入: candidates [10,1,2,7,6,…...
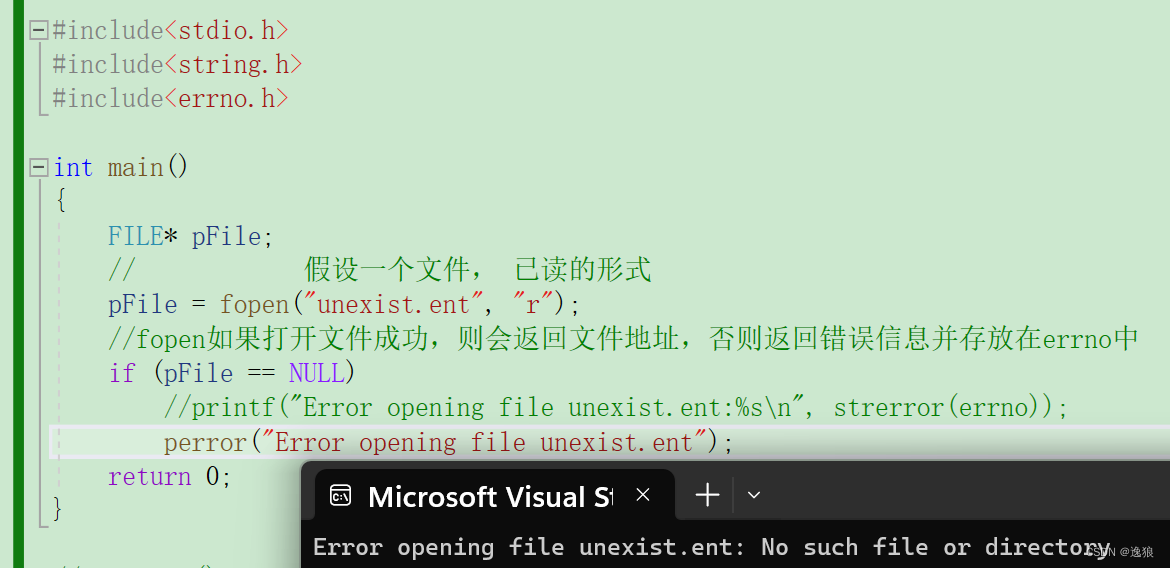
【c语言】字符函数和字符串函数(下)
前言 书接上回 【c语言】字符函数和字符串函数(上) 上一篇讲解的strcpy、strcat、strcmp函数的字符串长度是不受限制的 而本篇strncpy、strncat、strcnmp函数的字符串长度是受限制的 欢迎关注个人主页:逸狼 创造不易,可以点点赞吗~ 如有错误,…...

基于Java的艺培管理解决方案
✍✍计算机毕业编程指导师 ⭐⭐个人介绍:自己非常喜欢研究技术问题!专业做Java、Python、微信小程序、安卓、大数据、爬虫、Golang、大屏等实战项目。 ⛽⛽实战项目:有源码或者技术上的问题欢迎在评论区一起讨论交流! ⚡⚡ Java、…...

Python算法题集_实现 Trie [前缀树]
Python算法题集_实现 Trie [前缀树] 题208:实现 Trie (前缀树)1. 示例说明2. 题目解析- 题意分解- 优化思路- 测量工具 3. 代码展开1) 标准求解【定义数据类默认字典】2) 改进版一【初始化字典无额外类】3) 改进版二【字典保存结尾信息无额外类】 4. 最优算法5. 相关…...

pytorch简单新型模型测试参数
import torch from torch.nn import Conv2d,MaxPool2d,Sequential,Flatten,Linear import torchvision import torch.optim.optimizer from torch.utils.data import DataLoader,dataset from torch import nn import torch.optim.optimizer# 建模 model nn.Linear(2,1)#损失 …...
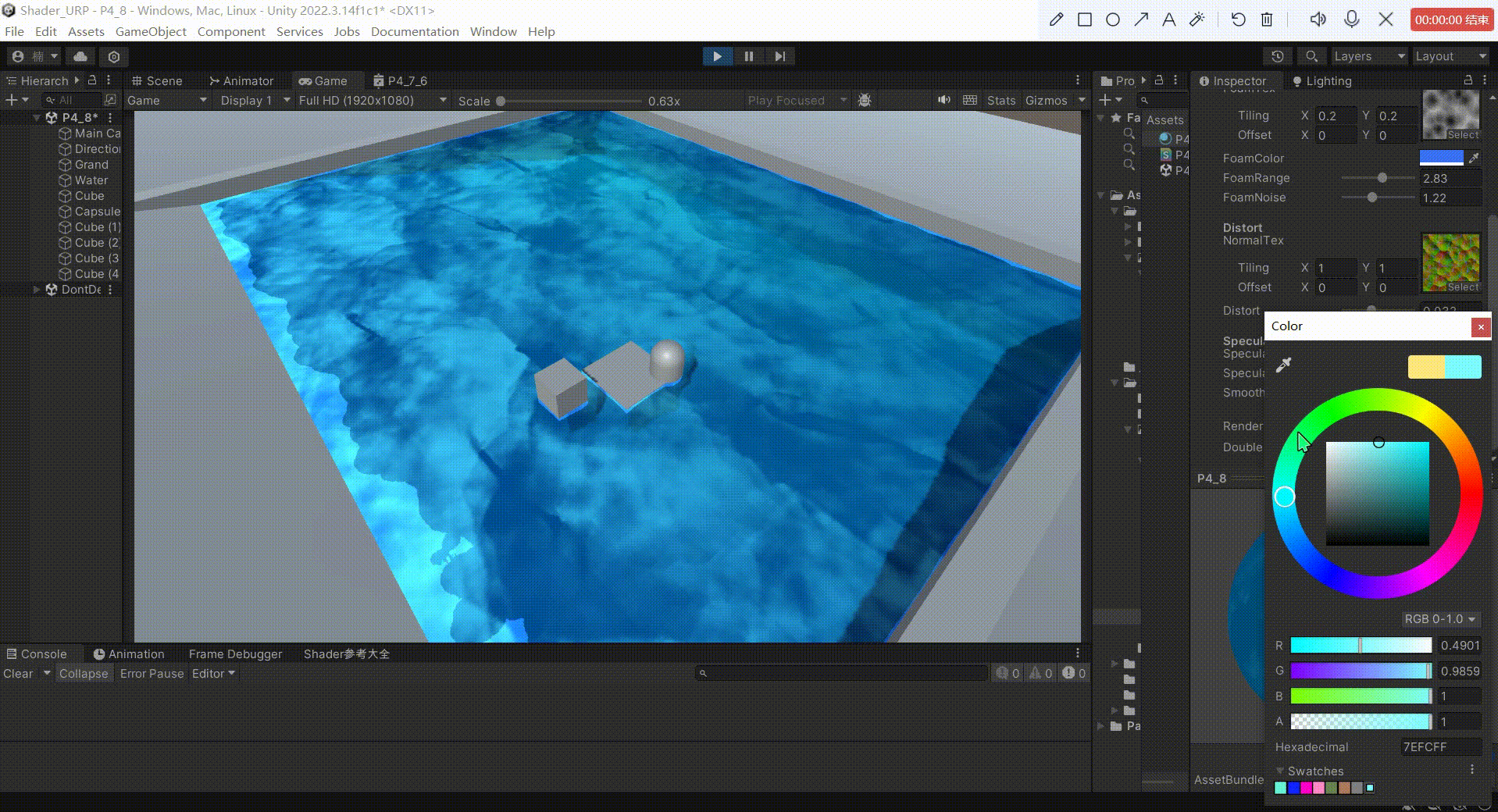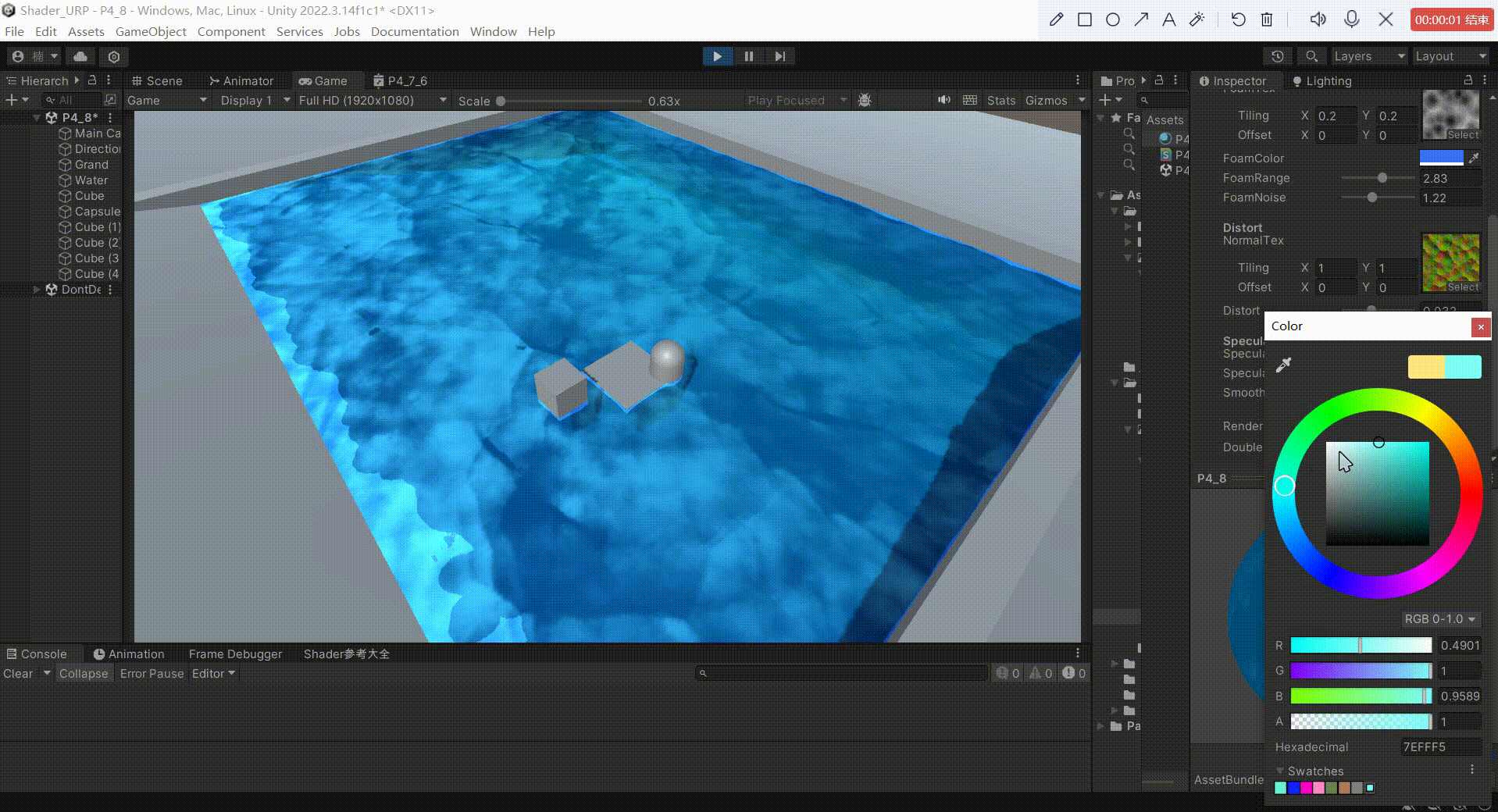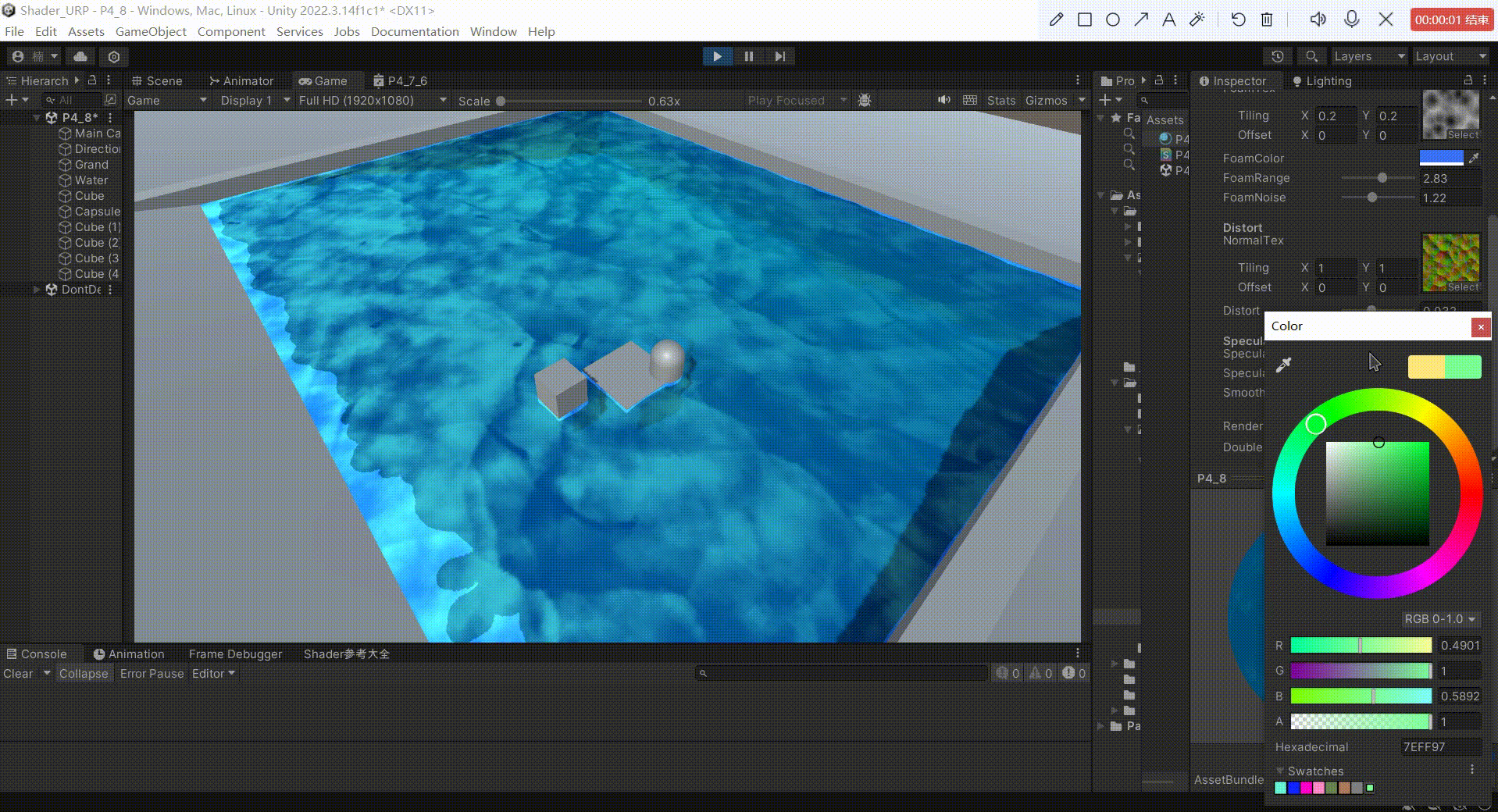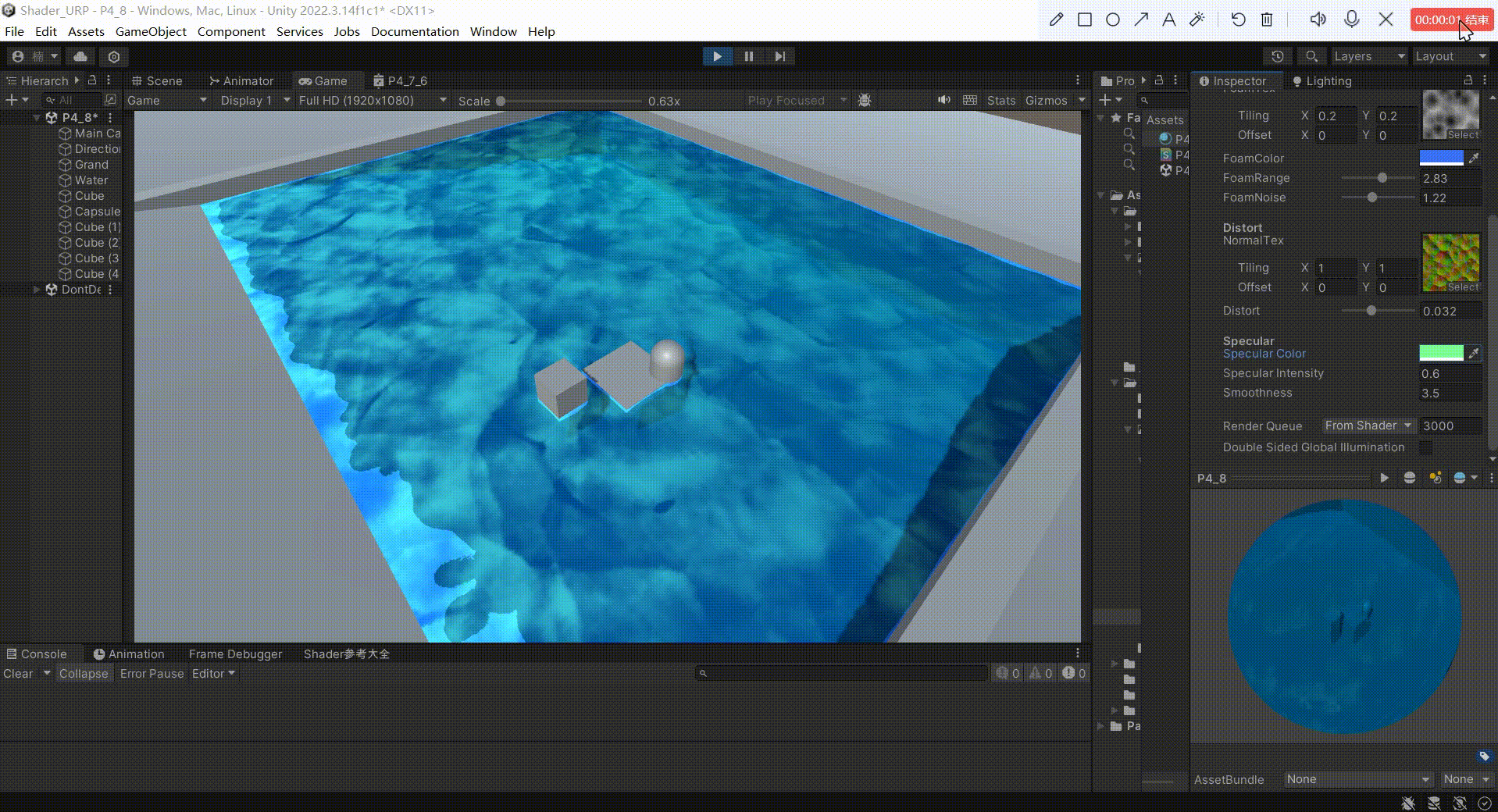
Unity中URP下实现水体(水面高光)
文章目录 前言一、实现高光反射原理1、原理:2、公式: 二、实现1、定义 _SpecularColor 作为高光反射的颜色2、定义 _SpecularIntensity 作为反射系数,控制高光反射的强度3、定义 _Smoothness 作为高光指数,用于模型高光范围4、模拟…...

26.HarmonyOS App(JAVA)列表对话框
列表对话框的单选模式: //单选模式 // listDialog.setSingleSelectItems(new String[]{"第1个选项","第2个选项"},1);//单选 // listDialog.setOnSingleSelectListener(new IDialog.ClickedListener() { // Override …...

Prompt Tuning、P-Tuning、Prefix Tuning的区别
一、Prompt Tuning、P-Tuning、Prefix Tuning的区别 1. Prompt Tuning(提示调优) 核心思想:固定预训练模型参数,仅学习额外的连续提示向量(通常是嵌入层的一部分)。实现方式:在输入文本前添加可训练的连续向量(软提示),模型只更新这些提示参数。优势:参数量少(仅提…...

突破不可导策略的训练难题:零阶优化与强化学习的深度嵌合
强化学习(Reinforcement Learning, RL)是工业领域智能控制的重要方法。它的基本原理是将最优控制问题建模为马尔可夫决策过程,然后使用强化学习的Actor-Critic机制(中文译作“知行互动”机制),逐步迭代求解…...

【WiFi帧结构】
文章目录 帧结构MAC头部管理帧 帧结构 Wi-Fi的帧分为三部分组成:MAC头部frame bodyFCS,其中MAC是固定格式的,frame body是可变长度。 MAC头部有frame control,duration,address1,address2,addre…...

视频字幕质量评估的大规模细粒度基准
大家读完觉得有帮助记得关注和点赞!!! 摘要 视频字幕在文本到视频生成任务中起着至关重要的作用,因为它们的质量直接影响所生成视频的语义连贯性和视觉保真度。尽管大型视觉-语言模型(VLMs)在字幕生成方面…...

HBuilderX安装(uni-app和小程序开发)
下载HBuilderX 访问官方网站:https://www.dcloud.io/hbuilderx.html 根据您的操作系统选择合适版本: Windows版(推荐下载标准版) Windows系统安装步骤 运行安装程序: 双击下载的.exe安装文件 如果出现安全提示&…...

uniapp微信小程序视频实时流+pc端预览方案
方案类型技术实现是否免费优点缺点适用场景延迟范围开发复杂度WebSocket图片帧定时拍照Base64传输✅ 完全免费无需服务器 纯前端实现高延迟高流量 帧率极低个人demo测试 超低频监控500ms-2s⭐⭐RTMP推流TRTC/即构SDK推流❌ 付费方案 (部分有免费额度&#x…...

【数据分析】R版IntelliGenes用于生物标志物发现的可解释机器学习
禁止商业或二改转载,仅供自学使用,侵权必究,如需截取部分内容请后台联系作者! 文章目录 介绍流程步骤1. 输入数据2. 特征选择3. 模型训练4. I-Genes 评分计算5. 输出结果 IntelliGenesR 安装包1. 特征选择2. 模型训练和评估3. I-Genes 评分计…...

CRMEB 中 PHP 短信扩展开发:涵盖一号通、阿里云、腾讯云、创蓝
目前已有一号通短信、阿里云短信、腾讯云短信扩展 扩展入口文件 文件目录 crmeb\services\sms\Sms.php 默认驱动类型为:一号通 namespace crmeb\services\sms;use crmeb\basic\BaseManager; use crmeb\services\AccessTokenServeService; use crmeb\services\sms\…...

LangFlow技术架构分析
🔧 LangFlow 的可视化技术栈 前端节点编辑器 底层框架:基于 (一个现代化的 React 节点绘图库) 功能: 拖拽式构建 LangGraph 状态机 实时连线定义节点依赖关系 可视化调试循环和分支逻辑 与 LangGraph 的深…...

uniapp 小程序 学习(一)
利用Hbuilder 创建项目 运行到内置浏览器看效果 下载微信小程序 安装到Hbuilder 下载地址 :开发者工具默认安装 设置服务端口号 在Hbuilder中设置微信小程序 配置 找到运行设置,将微信开发者工具放入到Hbuilder中, 打开后出现 如下 bug 解…...
