数据结构之二叉树的精讲
𝙉𝙞𝙘𝙚!!👏🏻‧✧̣̥̇‧✦👏🏻‧✧̣̥̇‧✦ 👏🏻‧✧̣̥̇:Solitary_walk
⸝⋆ ━━━┓
- 个性标签 - :来于“云”的“羽球人”。 Talk is cheap. Show me the code
┗━━━━━━━ ➴ ⷯ本人座右铭 : 欲达高峰,必忍其痛;欲戴王冠,必承其重。
👑💎💎👑💎💎👑
💎💎💎自💎💎💎
💎💎💎信💎💎💎
👑💎💎 💎💎👑 希望在看完我的此篇博客后可以对你有帮助哟👑👑💎💎💎👑👑 此外,希望各位大佬们在看完后,可以互相支持,蟹蟹!
👑👑👑💎👑👑👑
对二叉树的基本概念性的理解,若有不明白的友友们,可以看一下前期写的关于堆与二叉树的精讲
链接在此:
有了大家对二叉树的基本理解接下来,对以下知识的理解应该是易如反掌!
1.二叉树的链式结构的实现
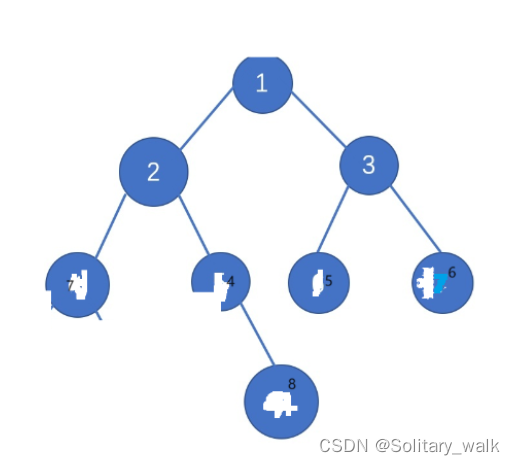
对于任何一个二叉树的节点来说:都是由值域,左孩子,右孩子构成,只不过对于某些节点而言左右孩子为空
1.1定义一个二叉树的结构体
typedef int BT_DataType;
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left; //左孩子struct BinaryTreeNode* right;//右孩子BT_DataType val; //值域}BT;1.2二叉树的链式结构
为了方便对二叉树的理解,我暂时手动创建节点,进行连接
BT* BT_Create()
{BT* n1 = BuyNode( 1);BT* n2 = BuyNode( 2);BT* n3 = BuyNode( 3);BT* n4 = BuyNode( 4);BT* n5 = BuyNode(5);BT* n6 = BuyNode( 6);BT* n7 = BuyNode( 7);BT* n8= BuyNode( 8);BT* n9 = BuyNode( 9);BT* n10 = BuyNode( 10);n1->left = n2;n1->right = n3;n2->right = n4;n3->left = n5;n3->right = n6;n2->left = n7;n4->left = n8;return n1;
}2.二叉树的遍历
2.1前序遍历(先序遍历)
先访问根节点,其次访问左子树,左后访问右子树,注意这是一个递归的定义。
见图如下:

代码:
void Pre_order(BT* root)
{if (root == NULL){printf("%c ", 'n');//返回n表示为空return;}printf("%d ", root->val);Pre_order(root->left);Pre_order(root->right);
}递归展开图的解释:
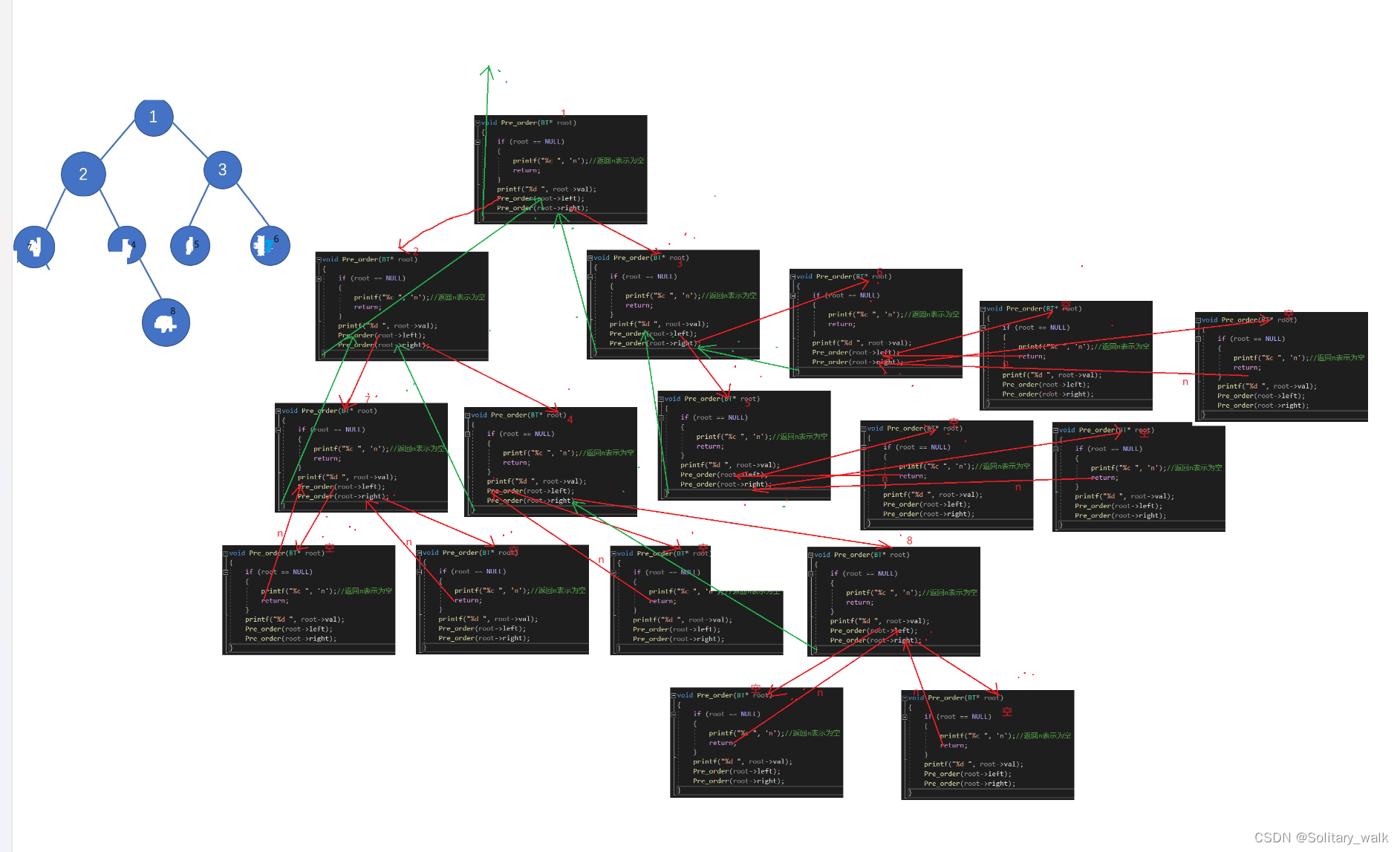
2.2中序遍历
先访问左子树,在访问根节点最后访问右子树,依然是一个递归的定义
分析如下:
代码:
void In_Order(BT* root)
{if (root == NULL){printf("%c ", 'n');//返回n表示为空return;}In_Order(root->left);printf("%d ", root->val);In_Order(root->right);
}2.3后续遍历
先访问左子树,再访问右子树,最后访问根节点,依然是递归定义
分析见下:
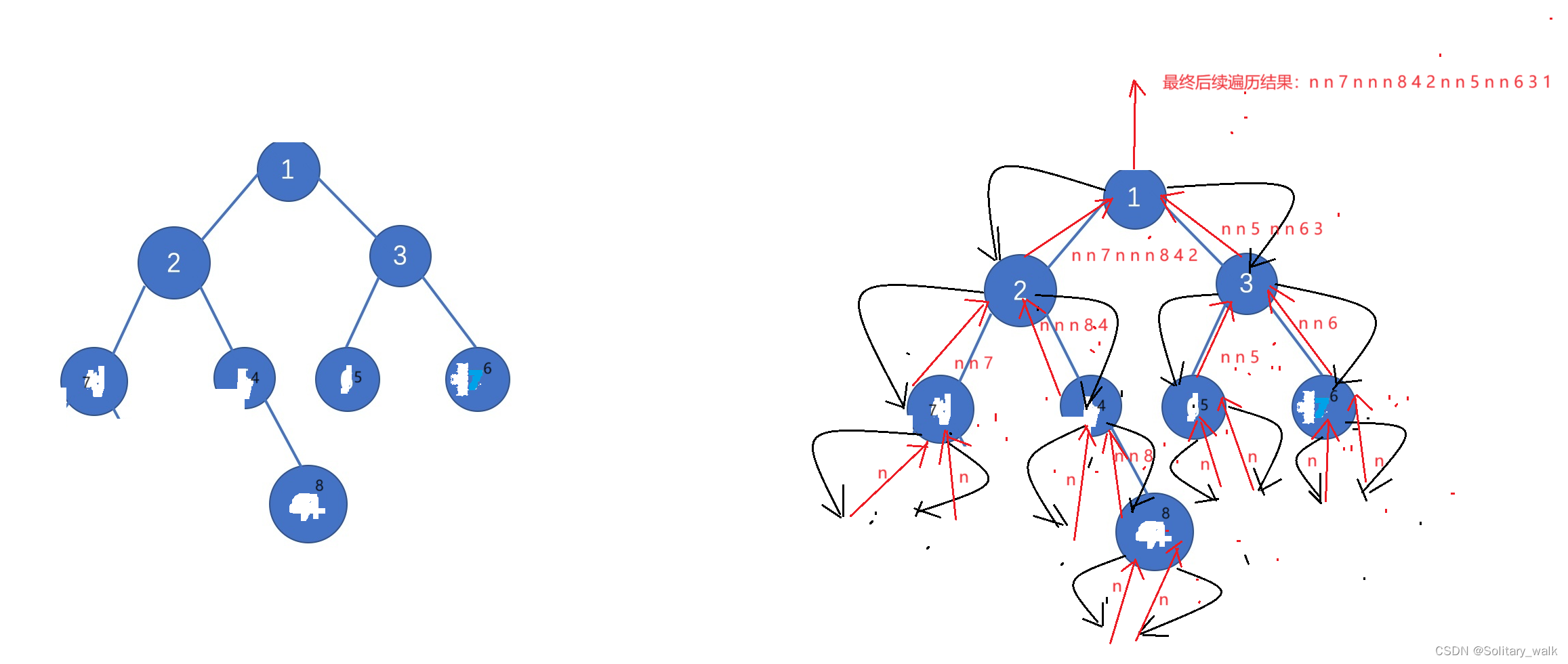
代码:
void Post_Order(BT* root)
{if (root == NULL){printf("%c ", 'n');//返回n表示为空return;}Post_Order(root->left);Post_Order(root->right);printf("%d ", root->val);}3.与二叉树相关节点的求解
3.1求二叉树所有节点个数
可能有些老铁们会说:直接进行计数就可以了:只有是当前节点不为空就让计数器(size)加一,采用前序遍历的方法。没错也可以这样但是这样有些坑需要注意一下否则一不小心就掉进坑里了。
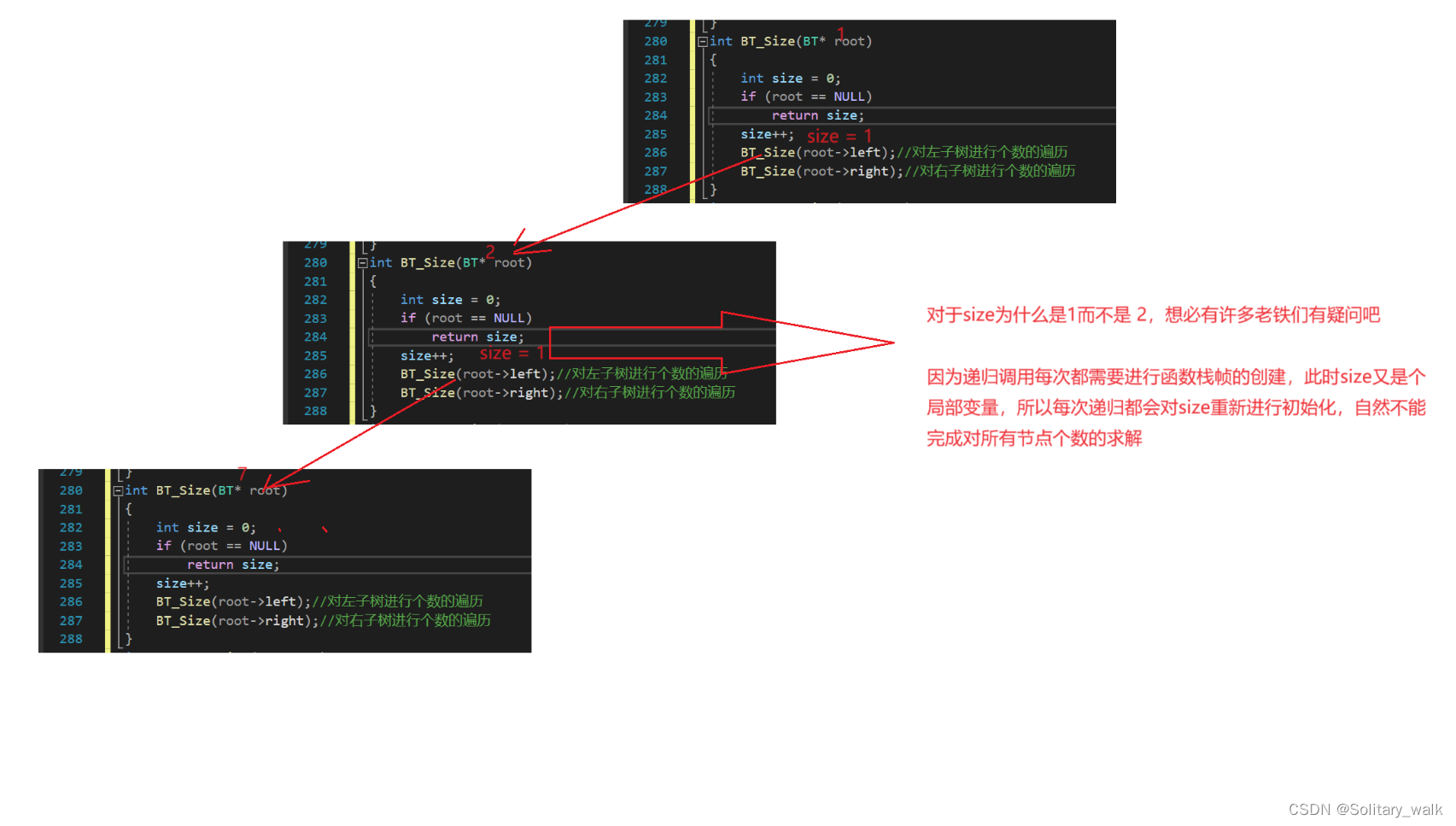
这时候可能有老铁会说,直接定义一个全局变量不就OK了,注意当我们连续调用BT_Size()这个函数进行求个数的话会有问题滴!
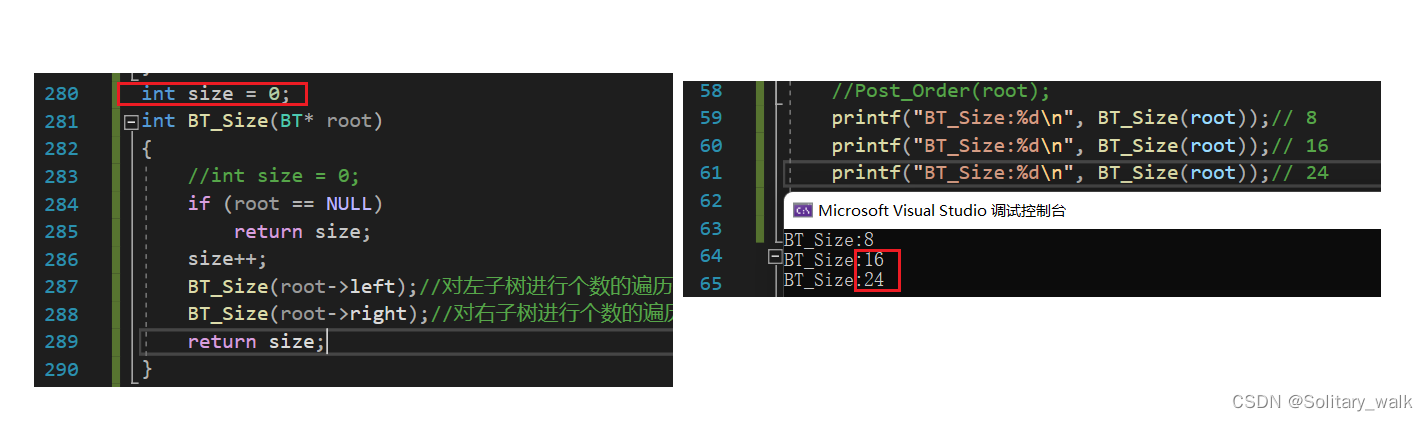
因为szie作为一个全局变量,第一调用确实为8没有错,但是当我们后续在进行调用的时候就需要把size 手动进行置零,(关于这个问题详解,感兴趣的友友们,可以看前期我写的博客:链接在此,自取,蟹蟹支持!)要不然只会在当前size = 8 的基础上进行相加,这也就是为什么最后会出现16,24的这样结果了,也就不以为奇了。
代码:
int size = 0;
int BT_Size(BT* root)
{//int size = 0;if (root == NULL)return size;size++;BT_Size(root->left);//对左子树进行个数的遍历BT_Size(root->right);//对右子树进行个数的遍历return size;
}运行结果:
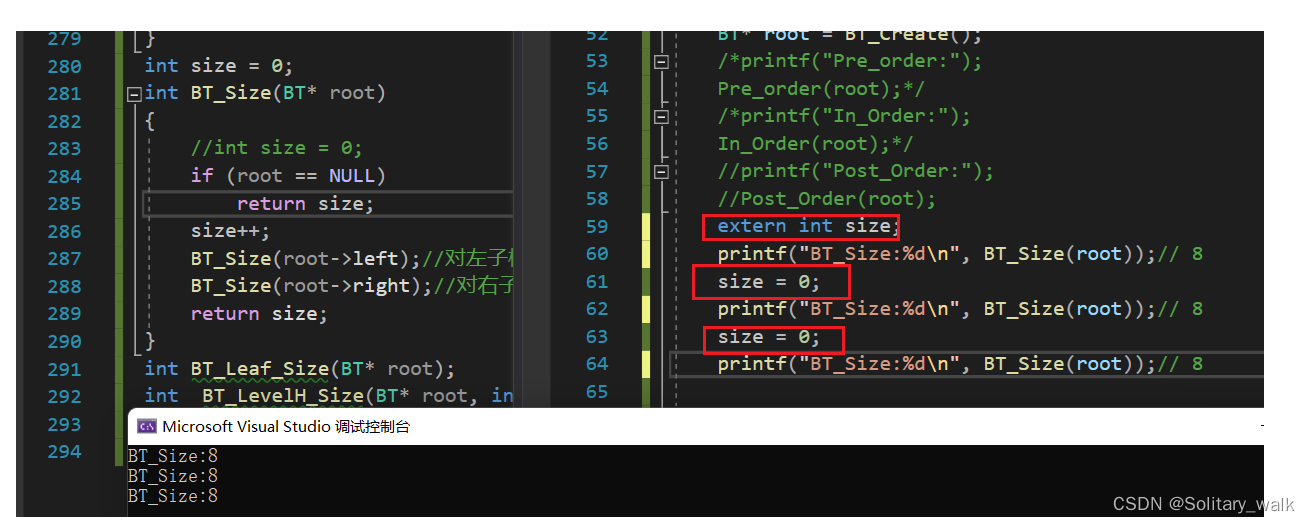
3.2求二叉树叶节点个数
既然是让咱求叶节点个数,咱就需要知道什么是叶节点:度为0的节点(没有左孩子,也没有右孩子的节点)
通过前面对二叉树的遍历咱们应该渐渐对递归要有些体悟了,当一个问题很大的时候,可以化大为小,化繁为简。这样岂不是很爽!

分析见下: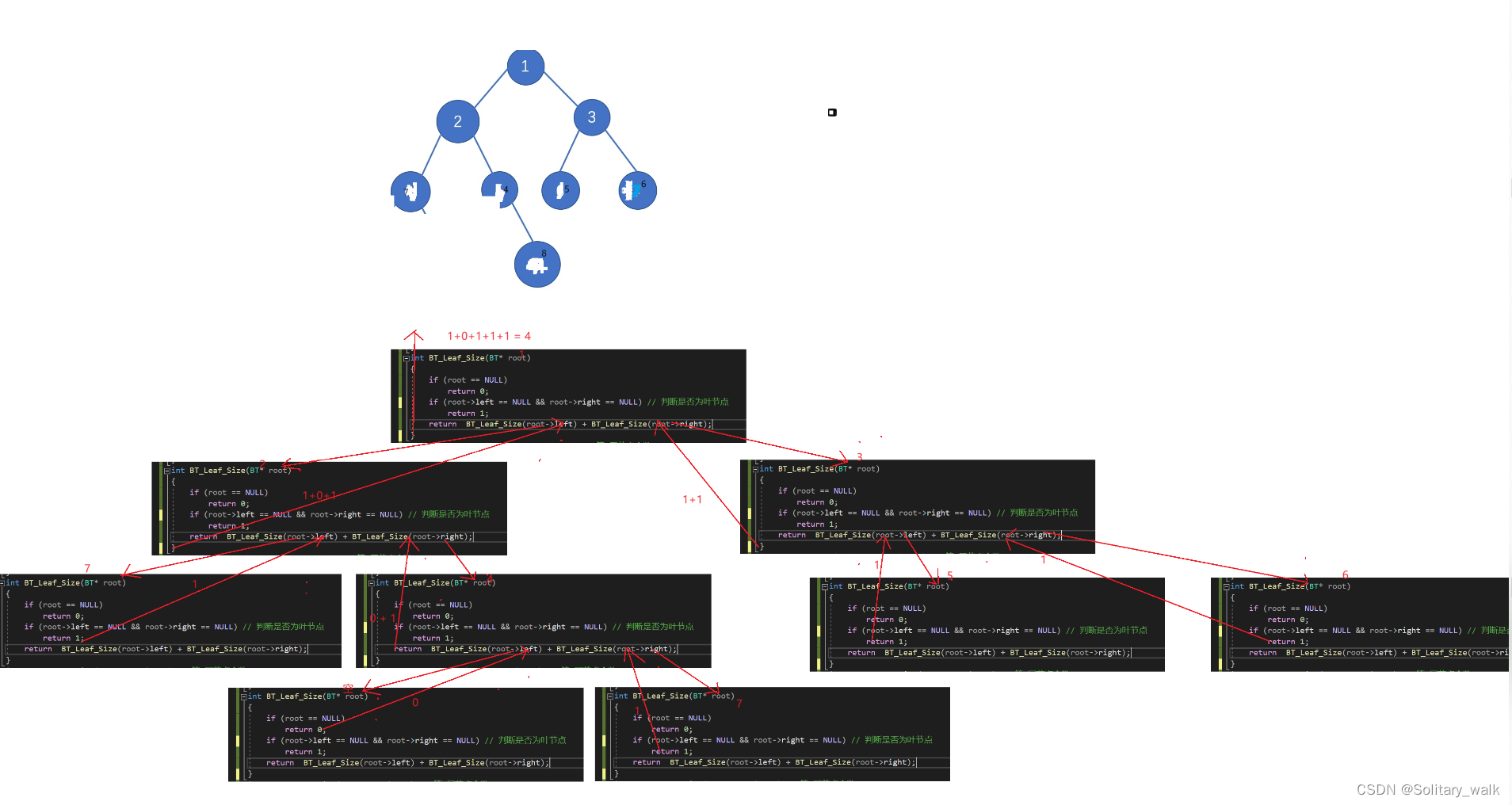
代码:
int BT_Leaf_Size(BT* root)
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL) // 判断是否为叶节点return 1;return BT_Leaf_Size(root->left) + BT_Leaf_Size(root->right);
}3.3求二叉树第H层节点个数
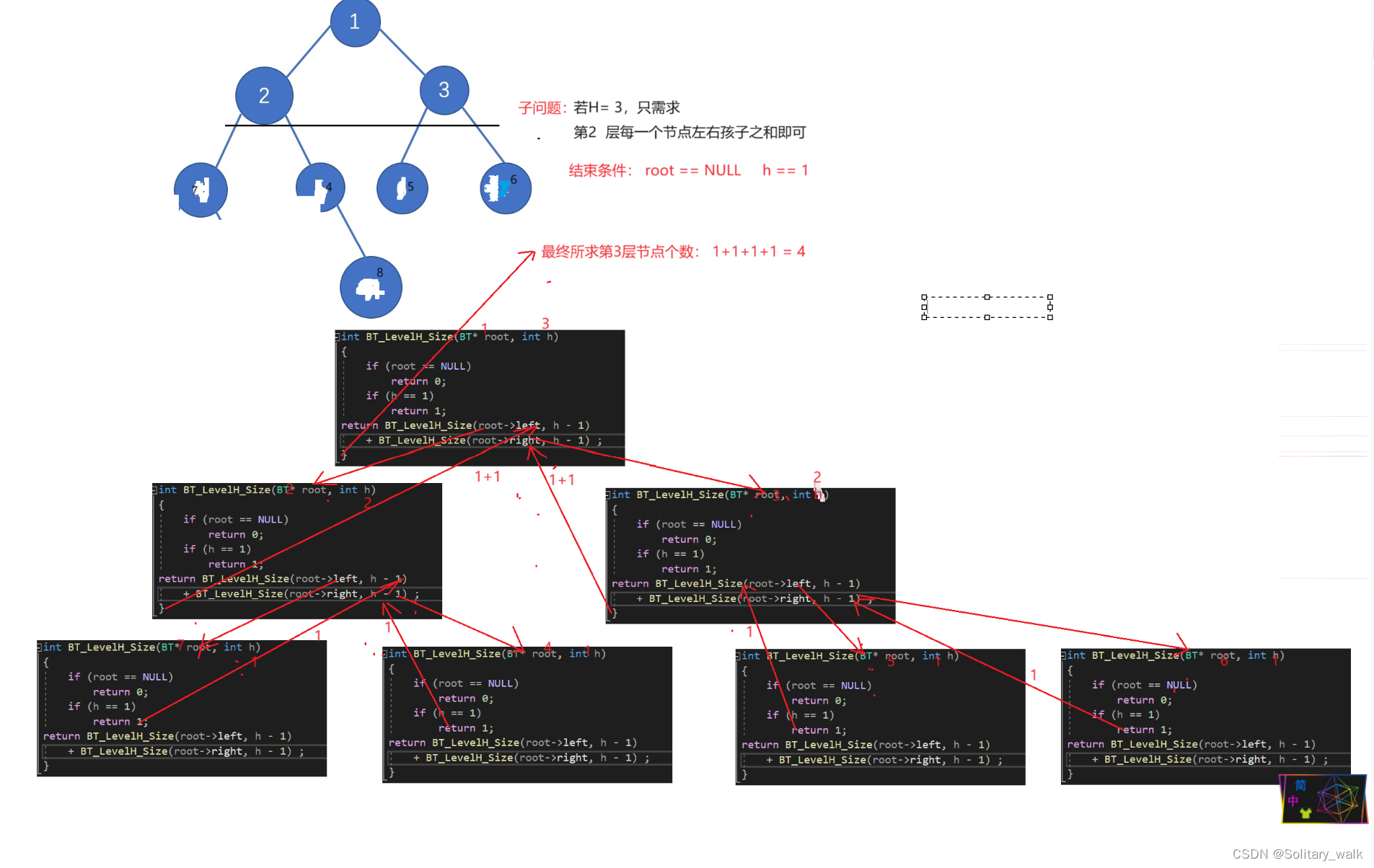
假设根节点所在层次就是第一层,依次下推,第H层的每个节点必然是第(H-1)层节点的左右孩子,这不就解决问题了嘛:求二叉树第H层节点个数转化为求二叉树第H-1层每个节点的左右孩子之和不就OK了。
分析见下:
代码:
int BT_LevelH_Size(BT* root, int h)
{if (root == NULL)return 0;if (h == 1)return 1;
return BT_LevelH_Size(root->left, h - 1)+ BT_LevelH_Size(root->right, h - 1) ;
}4.二叉树高度的求解
对于一个二叉树而言,树的高度是左子树与右子树相比高度最大的一个再加1
还是如此,借助递归思想
子问题:左子树与右子树相比高度最大的一个再加1
结束条件:判断当前节点是否为空,其次当前节点是否为叶节点
分析见下:
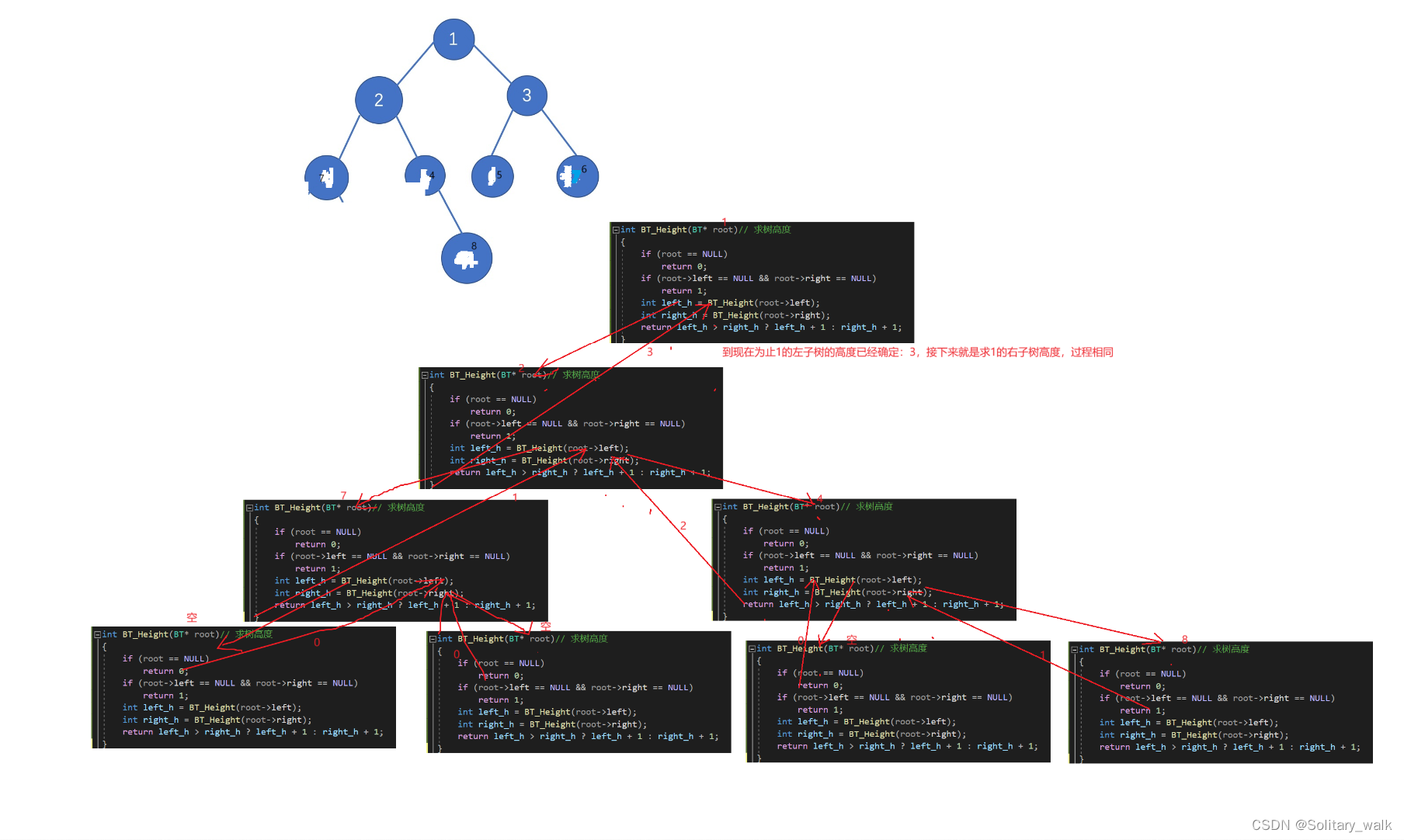
代码:
int BT_Height(BT* root)// 求树高度
{if (root == NULL)return 0;if (root->left == NULL && root->right == NULL)return 1;int left_h = BT_Height(root->left);int right_h = BT_Height(root->right);return left_h > right_h ? left_h + 1 : right_h + 1;
}5.二叉树的销毁
注意这是链式二叉树,不能直接进行删除,更为直接的是采用后续遍历来进行销毁
代码:
void BT_Destroy(BT* root)
{if (root == NULL)return;BT_Destroy(root->left);BT_Destroy(root->right);free(root);
}6.二叉树的层次遍历
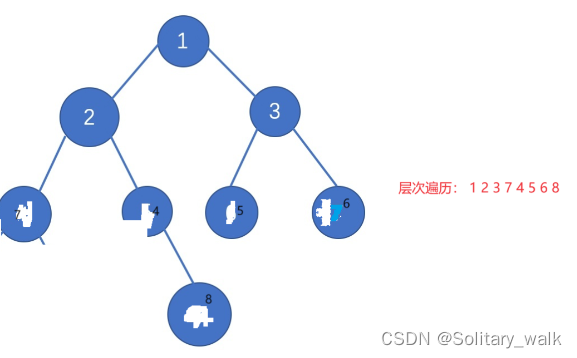
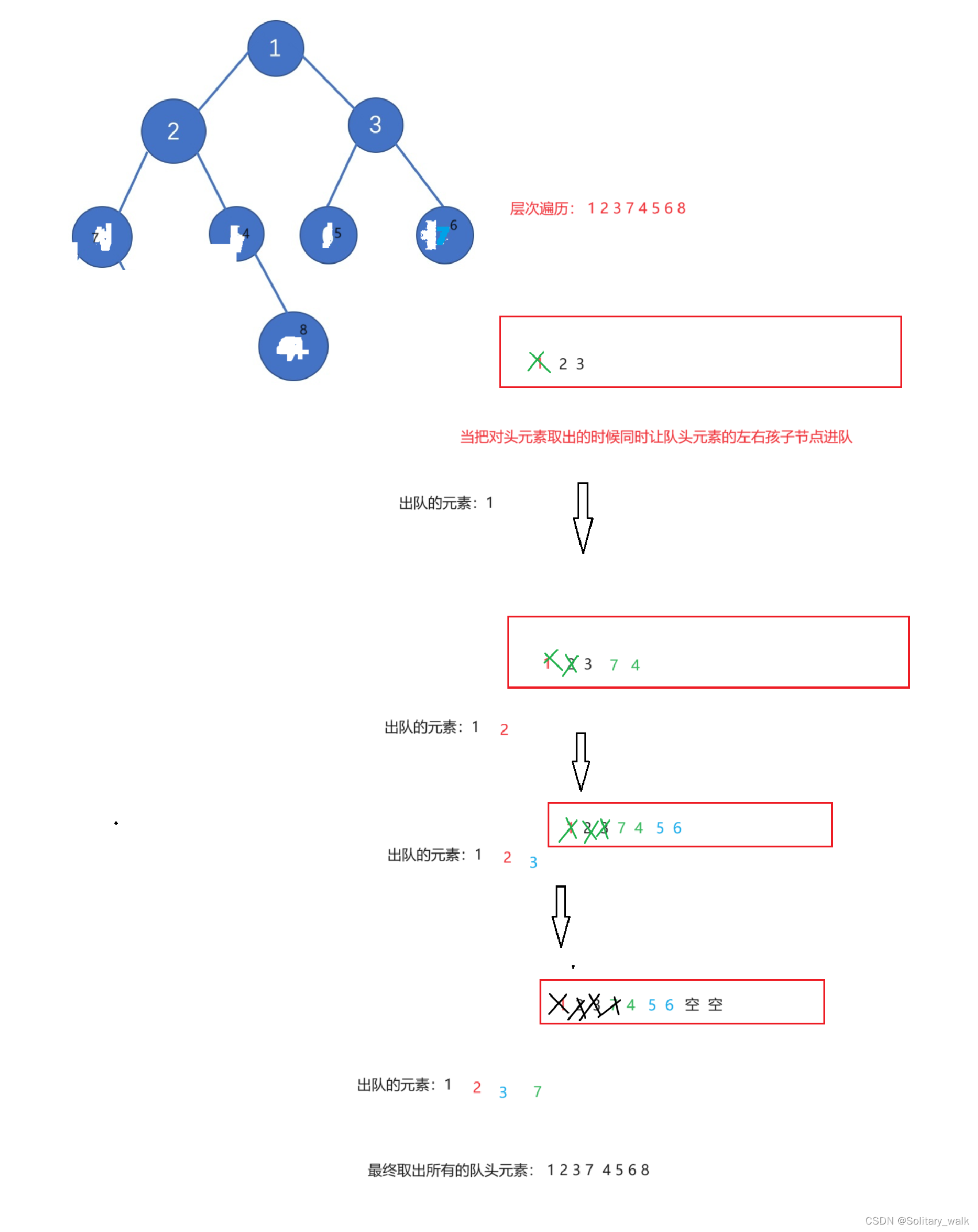
对于二叉树的层次遍历很显然就是一层一层进行遍历,在这里借助队的性质先进先出,来实现对二叉树的层次遍历
当队头元素出队的时候同时让队头元素的左右孩子节点也进队
这里需要借助咱们之前写的队列的相关代码才可以玩哟!
代码:
void Level_order(BT* root)
{Queque q;QuqueInit(&q);QuquePush(&q, root);while (!QuequeEmpty(&q)){BT* front = QuequeFront(&q);//取队头元素if (front)printf("%d ", front->val);QuquePop(&q);//删除队头元素//队头元素的左右孩子进队if (front) {QuquePush(&q, front->left);QuquePush(&q, front->right);}}QuqueDestroy(&q);
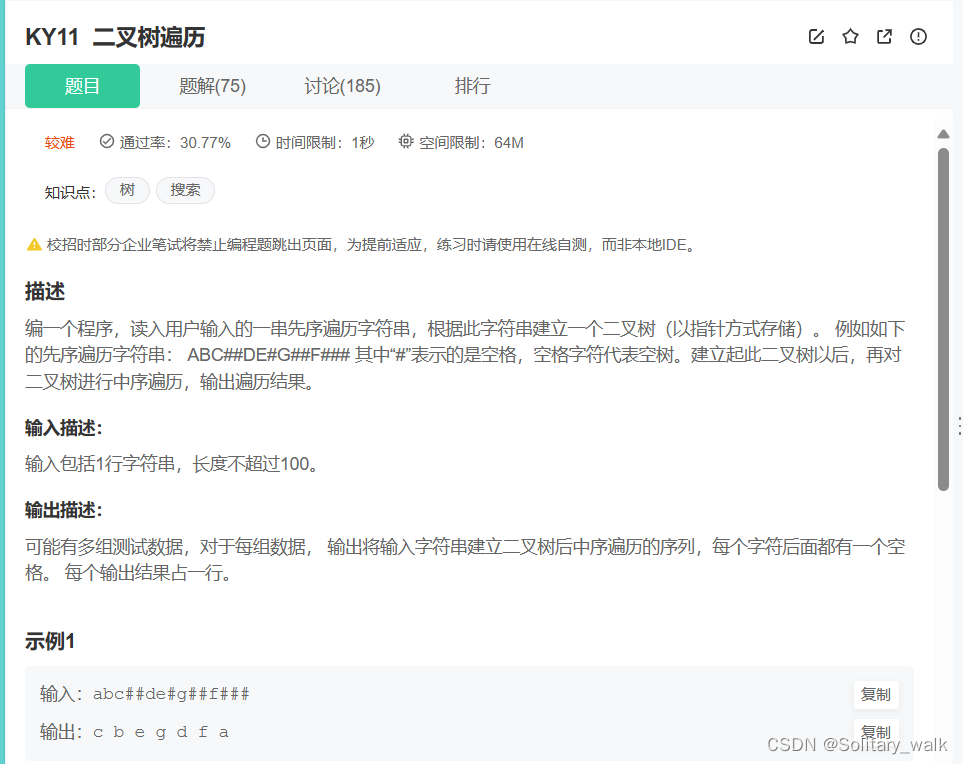
}7.借助二叉树前序遍历的结果实现对二叉树的构建
分析: 还是分治的思想,层层递归,直到遇到空返回,把每一个节点看作一个新的根节点,只要当前节点不为空,就继续先序遍历
首先这是一个IO型的,所以完全需要自己手撕代码,
先把当前字符串的内容进行接收
其次利用递归:先序建立二叉树
子问题:先序建立 结束条件:遇到空,直接返回
最后利用递归写一个中序遍历
辅助:需要我们每一个数据开辟节点
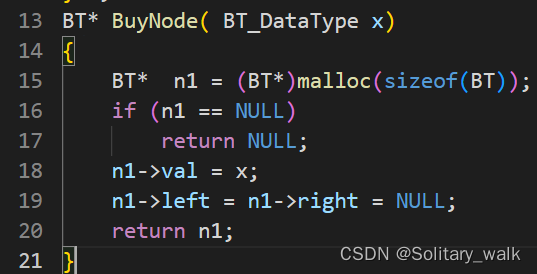
定义一个二叉树的结构体:
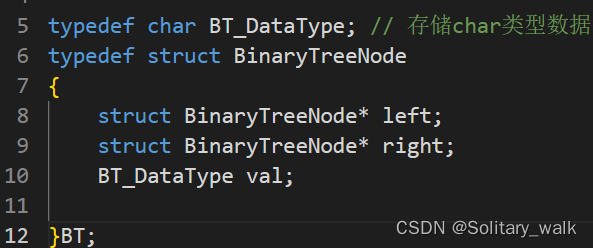
递归建立二叉树:
注意这里必须是 (*pi)++,不能是 *pi++。因为是递归调用每一次都需要进行栈帧建立,这样就不能做保证下标正确性,问题本质同二叉树求节点个数中的size
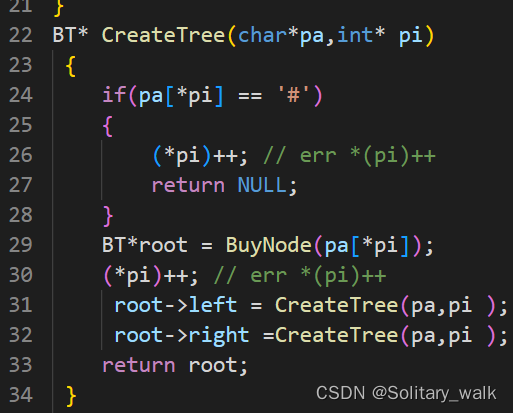
完整代码:
#include <stdio.h>
#include <stdlib.h>
#include <string.h>typedef char BT_DataType; // 存储char类型数据
typedef struct BinaryTreeNode
{struct BinaryTreeNode* left;struct BinaryTreeNode* right;BT_DataType val;}BT;
BT* BuyNode( BT_DataType x)
{BT* n1 = (BT*)malloc(sizeof(BT));if (n1 == NULL)return NULL;n1->val = x;n1->left = n1->right = NULL;return n1;
}
BT* CreateTree(char*pa,int* pi){if(pa[*pi] == '#'){(*pi)++; // err *(pi)++return NULL;}BT*root = BuyNode(pa[*pi]);(*pi)++; // err *(pi)++root->left = CreateTree(pa,pi );root->right =CreateTree(pa,pi );return root;}void In_Order(BT*root){if(root == NULL)return ;In_Order(root->left);printf("%c ",root->val);In_Order(root->right);}int main()
{char a[100];scanf("%s",a);int i = 0;// 下标访问数组BT* root = CreateTree(a,&i);In_Order(root);
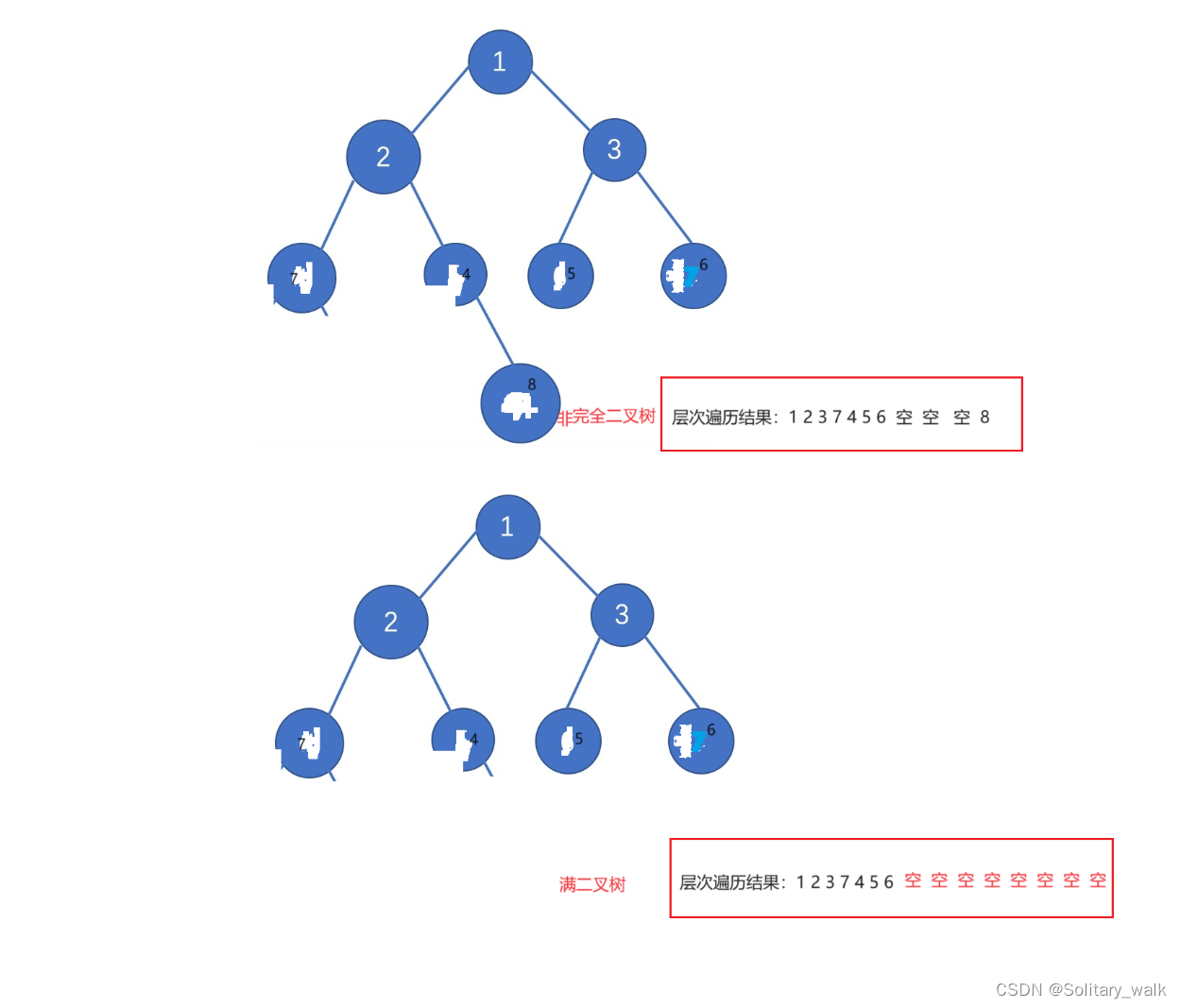
}8.判断一棵树是否为完全二叉树
对于这个,可以借助层次遍历的思想来玩。只要是在出队的时候连续全部为空即为完全二叉树;否则就不是完全二叉树
代码:
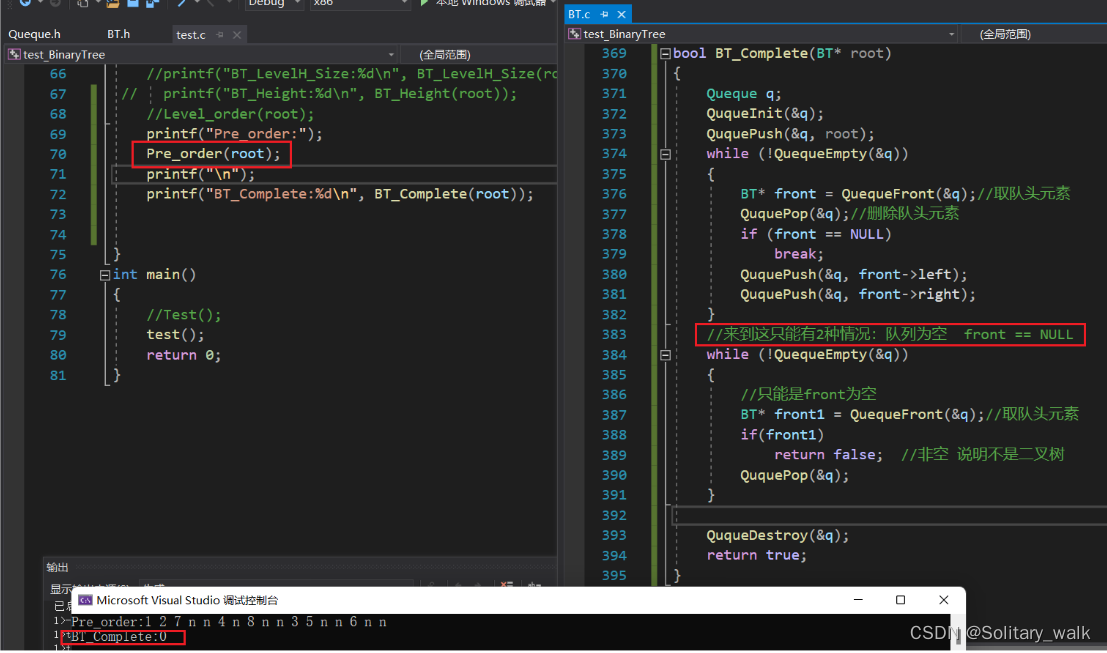
bool BT_Complete(BT* root)
{Queque q;QuqueInit(&q);QuquePush(&q, root);while (!QuequeEmpty(&q)){BT* front = QuequeFront(&q);//取队头元素QuquePop(&q);//删除队头元素if (front == NULL)break;QuquePush(&q, front->left);QuquePush(&q, front->right);}//来到这只能有2种情况:队列为空 front == NULLwhile (!QuequeEmpty(&q)){//只能是front为空BT* front1 = QuequeFront(&q);//取队头元素if(front1)return false; //非空 说明不是二叉树QuquePop(&q);}QuqueDestroy(&q);return true;
}9:二叉树的查找
查找某个节点的值是否存在,若存在则返回该节点的地址,否则返回NULL
可以用先序来遍历
错误示例:当我想查找3这个节点时候
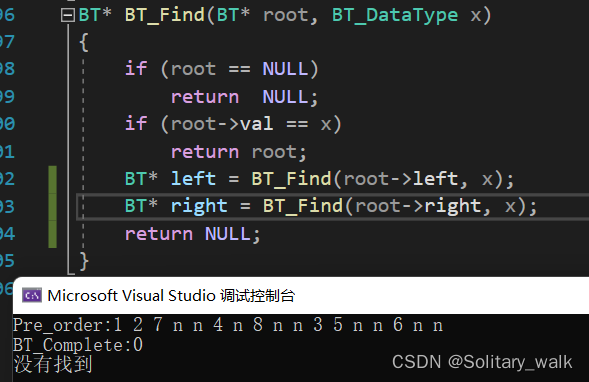
相信有不少老铁们一开始就会这样写吧,但是明明3这个节点存在为什么会没有找到呢?
其实通过我们调试发现这样写的逻辑是有Bug的,及时当要查找的节点存在时,也会造成把已找到的节点覆盖掉,其实这个查找逻辑的代码重在对return 返回的考察
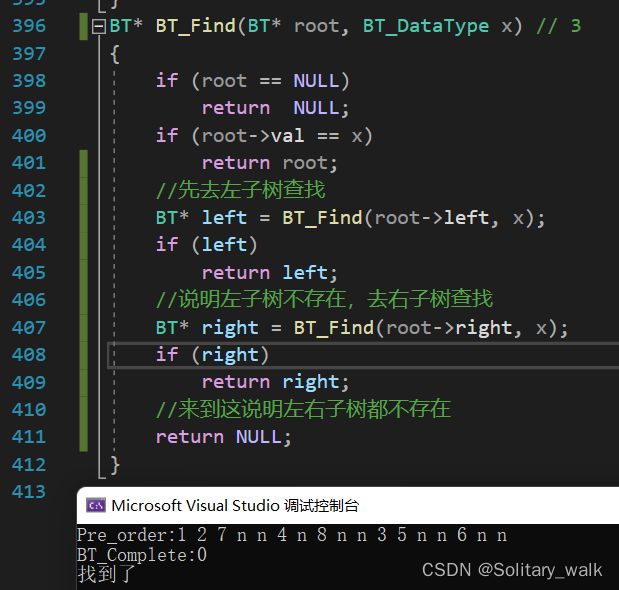
正确代码:
BT* BT_Find(BT* root, BT_DataType x) // 3
{if (root == NULL)return NULL;if (root->val == x)return root; //先去左子树查找BT* left = BT_Find(root->left, x);if (left)return left;//说明左子树不存在,去右子树查找BT* right = BT_Find(root->right, x);if (right)return right;//来到这说明左右子树都不存在return NULL;
}运行结果:
10.二叉树相关OJ的练习
10.1 单值二叉树
解题分析:
其实一个遍历就直接搞定了。拿双亲节点的值与孩子节点对应的值进行比较,若是不相等直接 return false
是不是看着比较简单,但是写起来是有坑滴!

运行结果:
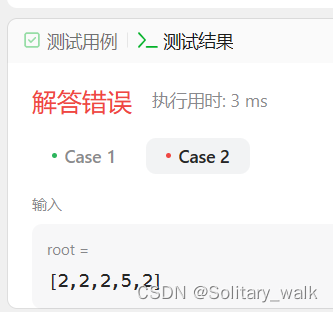
其实走读一遍代码大概就找到问题所在了:return 语句返回是返回到调用当前函数的上一个函数里,并不是直接返回到最外层
这个问题的本质同二叉树查找指定数据是一样的
OJ代码:
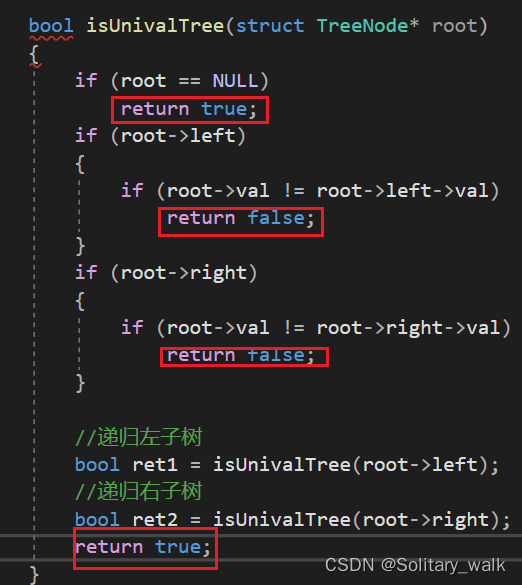
bool isUnivalTree(struct TreeNode* root)
{if(root == NULL)return true;if(root->left){if(root->val != root->left->val)return false;}if(root->right){if(root->val != root->right->val)return false;}//递归左子树bool ret1 = isUnivalTree(root->left);//递归右子树bool ret2= isUnivalTree(root->right);return ret1 && ret2;
}10.2 判断2个二叉树是否相同
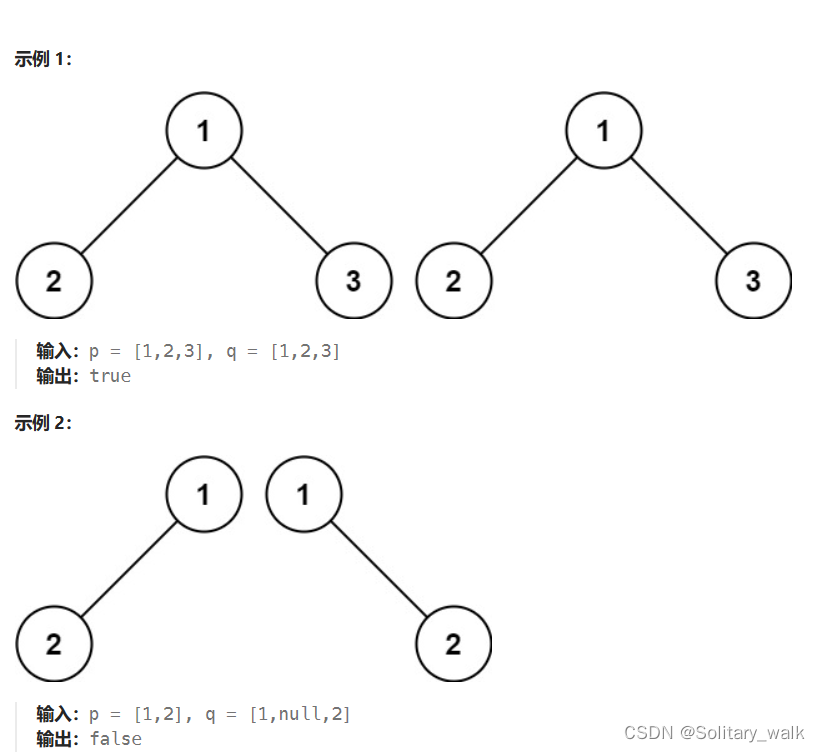
解题分析:
采用遍历的方式,根节点与根节点进行对比,左孩子与左孩子对比,右孩子与右孩子对比,注意是对比val而不是对比节点所对应的地址
OJ代码:
bool isSameTree(struct TreeNode* p, struct TreeNode* q){if(p == NULL &&q == NULL)return true;if(p == NULL || q == NULL)return false;//来到这说明都不为空if(p->val != q->val)return false;return isSameTree(p->left,q->left) && isSameTree(p->right,q->right);//注意这里必须是 逻辑且的关系,不能是逻辑或
}OK,以上就是我今日要为大家分享的,希望各位都有得!对于二叉树这部分是数据结构初阶比较难的一部分了,初学的时候是不好理解,事事都有个过渡期,当然自己有空的时候也不要忘了敲敲代码!
相关文章:

数据结构之二叉树的精讲
𝙉𝙞𝙘𝙚!!👏🏻‧✧̣̥̇‧✦👏🏻‧✧̣̥̇‧✦ 👏🏻‧✧̣̥̇:Solitary_walk ⸝⋆ ━━━┓ - 个性标签 - :来于“云”的“羽球人”。…...
ETL是什么
一、ETL概念 ETL,是英文Extract-Transform-Load的缩写,用来描述将数据从来源端经过抽取(extract)、转换(transform)、加载(load)至目的端的过程。ETL一词较常用在数据仓库ÿ…...
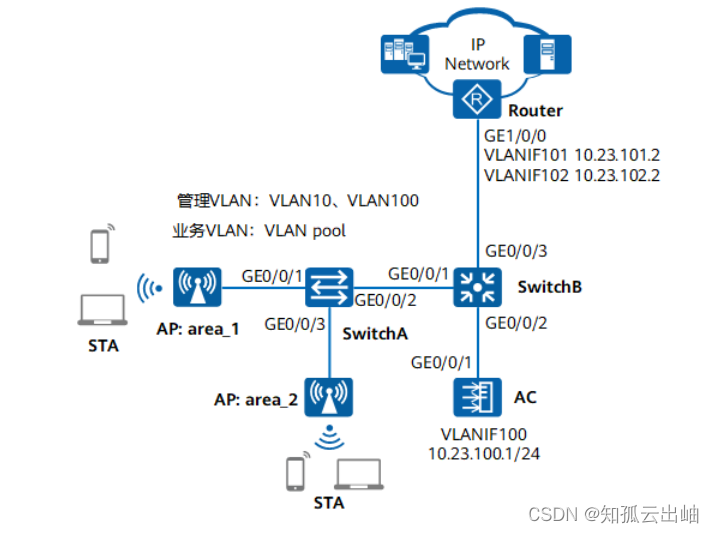
华为配置WLAN高密业务示例
配置WLAN高密业务示例 组网图形 图1 配置高密WLAN环境网络部署组网图 业务需求组网需求数据规划配置思路配置注意事项操作步骤配置文件 业务需求 体育场由于需要接入用户数量很大,AP间部署距离较小,因此AP间的干扰较大,可能导致用户上网网…...
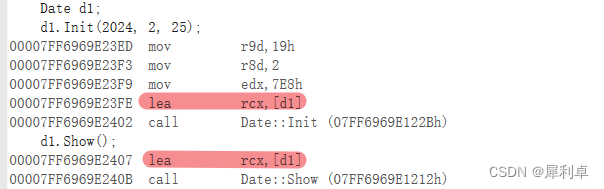
C++——类和对象(1)
1. 类 我们之前提及过C语言是面向过程的语言,其解决问题的方式是关注问题过程,然后逐步解决。而C是面向对象编程,聚焦于对象,依靠多个对象之间的交互关系解决问题。而类这个概念的引入则是面向对象的最深刻体现。 1.1 C中的结构体…...
vue+element ui上传图片到七牛云服务器
本来打算做一个全部都是前端完成的资源上传到七牛云的demo,但是需要获取token,经历了九九八十一难,最终还是选择放弃,token从后端获取(springboot)。如果你们有前端直接能解决的麻烦记得私我哦!…...
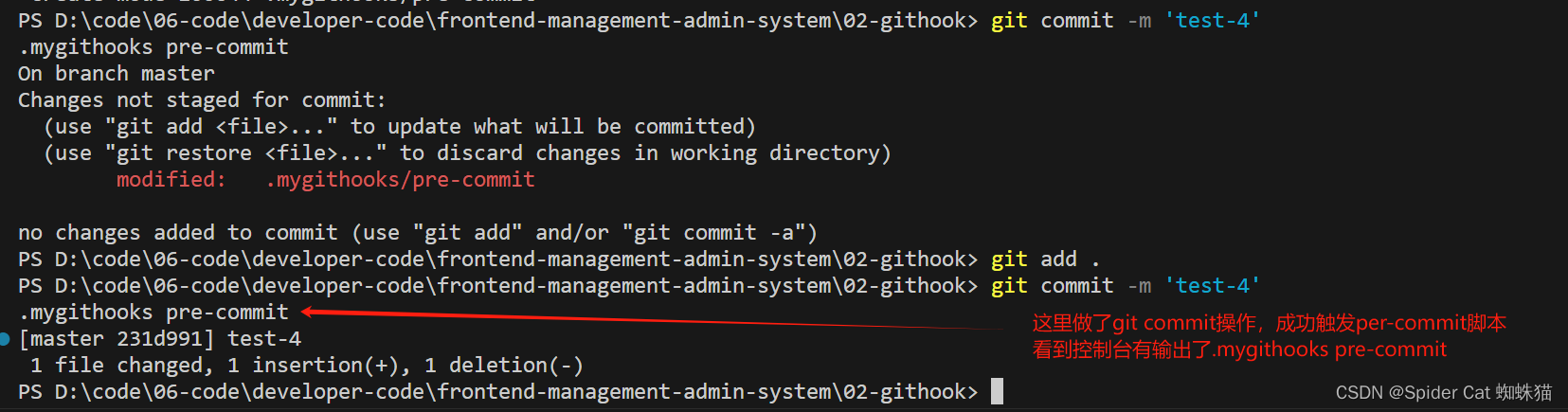
学不动系列-git-hooks和husky+lintstage
git-hooks 为了保证提交的代码符合规范,可以在上传代码时进行校验。常用husky来协助进行代码提交时的eslint校验。husky是基于git-hooks来实现,在使用husky之前,我们先来研究一下git-hooks。 构建git-hooks测试项目 需要使用git-hooks就需…...

K8S相关小技巧《四》
需求: 我作为Kubernetes的集群管理员,前一段时间有收到一个需求,需要我创建一个受限访问的用户kubeconfig,提供给跳板机的某用户。 该kubeconfig需要在非Kubernetes节点的某跳板机上由指定的非root用户使用,该用户仅能…...
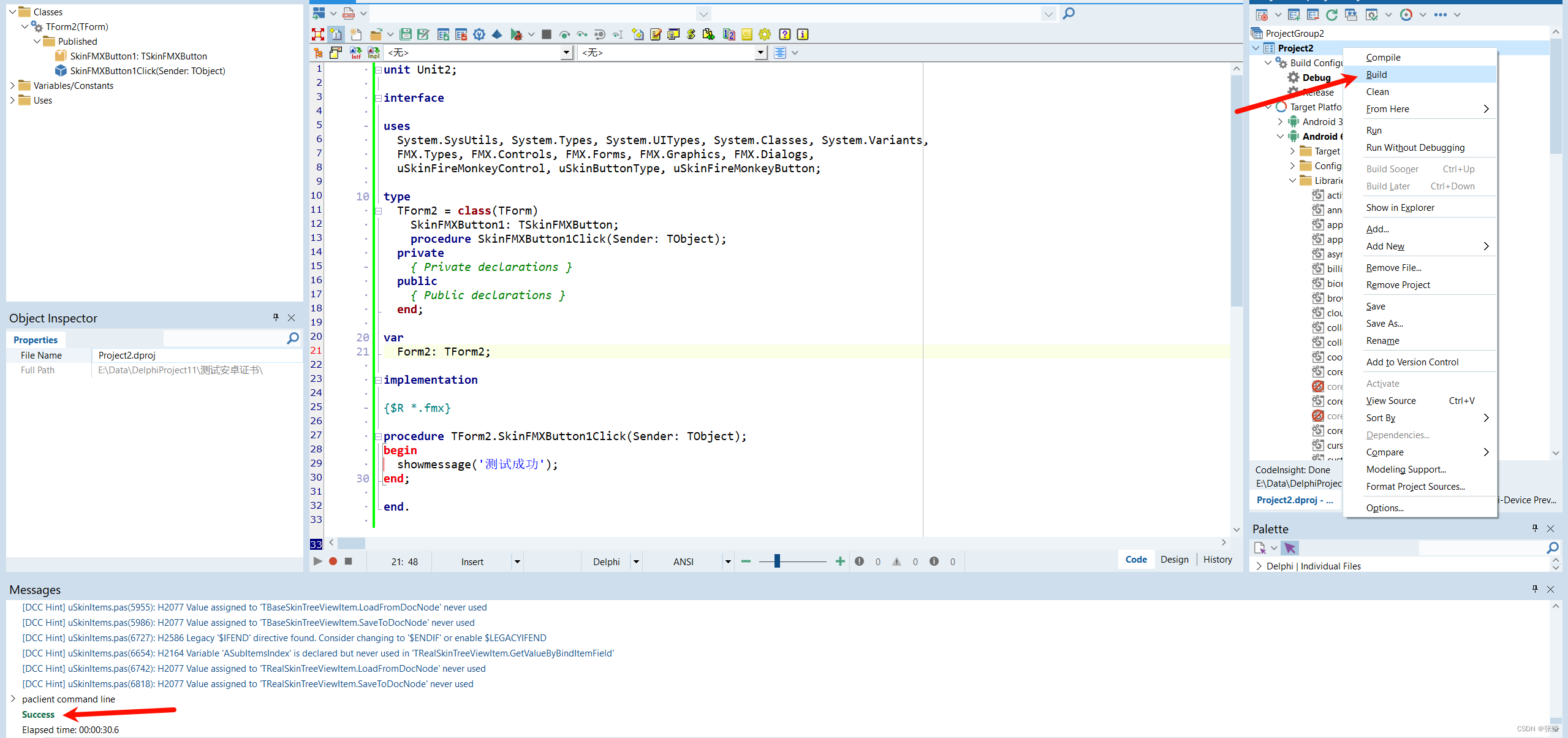
Delphi 报错 Type androidx.collection.ArraySet is defined multiple times
Delphi 11 建立一个新的 Multi-Device Application 编译成app的时候报错 报错信息 [PAClient Error] Error: E7688 Unable to execute "E:\Program\Java\jdk1.8.0_301\bin\java.exe" -cp "e:\program\embarcadero\studio\22.0\bin\Android\r8-3.3.28.jar"…...

Post请求中文乱码问题
url*************************************这里填写自己请求的网址 response requests.post(url, datajson.dumps(body),headersheader) r response.text print 打印乱码长这样: data:{“code”:0,“data”:{“end”:false,“message”:“{\n “ˆ—¡A”: [“…...

LeetCode -- 79.单词搜索
1. 问题描述 给定一个 m x n 二维字符网格 board 和一个字符串单词 word 。如果 word 存在于网格中,返回 true ;否则,返回 false 。 单词必须按照字母顺序,通过相邻的单元格内的字母构成,其中“相邻”单元格是那些水…...

单元测试、集成测试、系统测试有什么不同?
单元测试、集成测试和系统测试是软件测试开发中不可或缺的部分。 单元测试: 范围:单元测试是对软件中最小的可测试单元的测试,通常是函数、方法或类。 目的:它的目标是验证每个单独的单元是否按照预期工作,以增加代码…...
数据迁移DTS | 云上MySQL 数据库迁移至达梦数据库
引入 云上 MySQL 数据库 —> 向达梦国产化数据库迁移 下载&安装 达梦客户端工具 DM->可参考之前国产化专栏达梦文章 创建模式 在客户端分别依次执行以下命令脚本(这里没有通过客户端管理工具去创建达梦数据库的模式,当然也可以通过图形化界…...

Linux进程管理:(二)进程调度原语
文章说明: Linux内核版本:5.0 架构:ARM64 参考资料及图片来源:《奔跑吧Linux内核》 Linux 5.0内核源码注释仓库地址: zhangzihengya/LinuxSourceCode_v5.0_study (github.com) 进程调度的概念比较简单,…...

Compose 介绍
Compose 介绍 Android Compose 是 Google 官方推出的用于构建原生 Android UI 的现代工具包。它使用 Kotlin 语言编写,可以帮助开发人员更轻松、更快速地创建精美、响应式和高性能的 Android 应用。 Compose 的优势 声明式 UI: Compose 使用声明式 UI…...

5分钟搞定Python中函数的参数
函数的灵活性非常高,除了常规定义的位置参数以外,还支持默认参数、关键字参数、以及可变参数 ... 这样以来,不但能应对各种复杂的情况,甚至还可以简化调用者的代码。 位置参数 在调用函数时,一般会根据函数定义的参数…...
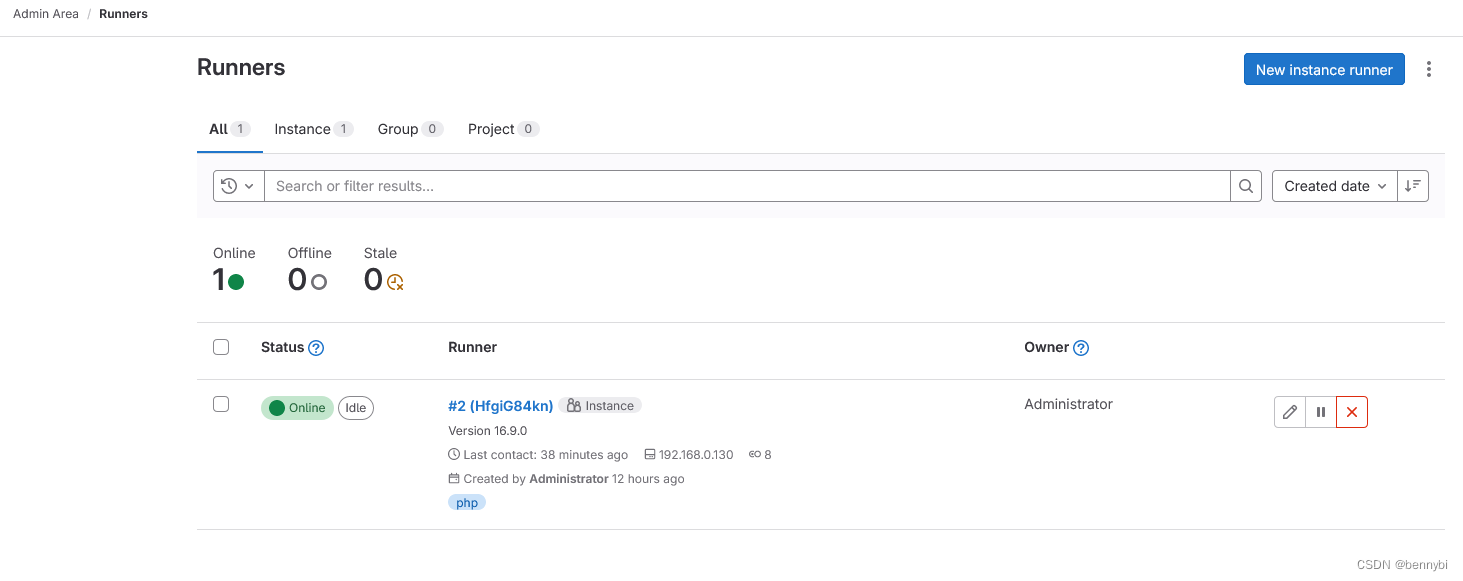
Gitlab: 私有化部署
目录 1. 说明 2. 资源要求 3. 安装 4. 配置实践 4.1 服务器 4.2 人员与项目 4.2 部署准备 4.2.1 访问变量及用户账号设置 4.2.2 Runner设置 4.2.3 要点 5. 应用项目 CI/CD 6. 参考 1. 说明 gitlab是一个强大且免费的代码管理/部署工具,能统一集成代码仓…...

深入理解Linux线程(LWP):概念、结构与实现机制(2)
🎬慕斯主页:修仙—别有洞天 ♈️今日夜电波:会いたい—Naomile 1:12━━━━━━️💟──────── 4:59 🔄 ◀️ ⏸ ▶️ ☰ &a…...

VBS脚本搞定,快速批量提取一堆Excel文件中的数据
1.需求诞生 小王就职于一家国有大型企业,工作业务十分繁忙,在处理企业某业务数据时,需要从上千个Excel文件中提取某一单元格位置的数据,并整理到另一个Excel文件。要说是这样的Excel文件仅有几个或者十几个也还好,手动…...
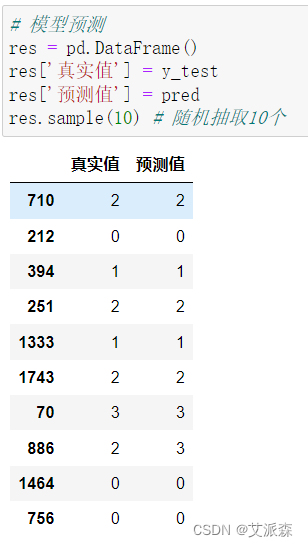
大数据分析案例-基于SVM支持向量机算法构建手机价格分类预测模型
🤵♂️ 个人主页:艾派森的个人主页 ✍🏻作者简介:Python学习者 🐋 希望大家多多支持,我们一起进步!😄 如果文章对你有帮助的话, 欢迎评论 💬点赞Ǵ…...

WPF 滑动条样式
效果图: 浅色: 深色: 滑动条部分代码: <Style x:Key"RepeatButtonTransparent" TargetType"{x:Type RepeatButton}"><Setter Property"OverridesDefaultStyle" Value"true"/&g…...

7.4.分块查找
一.分块查找的算法思想: 1.实例: 以上述图片的顺序表为例, 该顺序表的数据元素从整体来看是乱序的,但如果把这些数据元素分成一块一块的小区间, 第一个区间[0,1]索引上的数据元素都是小于等于10的, 第二…...

label-studio的使用教程(导入本地路径)
文章目录 1. 准备环境2. 脚本启动2.1 Windows2.2 Linux 3. 安装label-studio机器学习后端3.1 pip安装(推荐)3.2 GitHub仓库安装 4. 后端配置4.1 yolo环境4.2 引入后端模型4.3 修改脚本4.4 启动后端 5. 标注工程5.1 创建工程5.2 配置图片路径5.3 配置工程类型标签5.4 配置模型5.…...

Go 语言接口详解
Go 语言接口详解 核心概念 接口定义 在 Go 语言中,接口是一种抽象类型,它定义了一组方法的集合: // 定义接口 type Shape interface {Area() float64Perimeter() float64 } 接口实现 Go 接口的实现是隐式的: // 矩形结构体…...

在 Nginx Stream 层“改写”MQTT ngx_stream_mqtt_filter_module
1、为什么要修改 CONNECT 报文? 多租户隔离:自动为接入设备追加租户前缀,后端按 ClientID 拆分队列。零代码鉴权:将入站用户名替换为 OAuth Access-Token,后端 Broker 统一校验。灰度发布:根据 IP/地理位写…...

如何理解 IP 数据报中的 TTL?
目录 前言理解 前言 面试灵魂一问:说说对 IP 数据报中 TTL 的理解?我们都知道,IP 数据报由首部和数据两部分组成,首部又分为两部分:固定部分和可变部分,共占 20 字节,而即将讨论的 TTL 就位于首…...

docker 部署发现spring.profiles.active 问题
报错: org.springframework.boot.context.config.InvalidConfigDataPropertyException: Property spring.profiles.active imported from location class path resource [application-test.yml] is invalid in a profile specific resource [origin: class path re…...

让回归模型不再被异常值“带跑偏“,MSE和Cauchy损失函数在噪声数据环境下的实战对比
在机器学习的回归分析中,损失函数的选择对模型性能具有决定性影响。均方误差(MSE)作为经典的损失函数,在处理干净数据时表现优异,但在面对包含异常值的噪声数据时,其对大误差的二次惩罚机制往往导致模型参数…...

MySQL 部分重点知识篇
一、数据库对象 1. 主键 定义 :主键是用于唯一标识表中每一行记录的字段或字段组合。它具有唯一性和非空性特点。 作用 :确保数据的完整性,便于数据的查询和管理。 示例 :在学生信息表中,学号可以作为主键ÿ…...

python爬虫——气象数据爬取
一、导入库与全局配置 python 运行 import json import datetime import time import requests from sqlalchemy import create_engine import csv import pandas as pd作用: 引入数据解析、网络请求、时间处理、数据库操作等所需库。requests:发送 …...

0x-3-Oracle 23 ai-sqlcl 25.1 集成安装-配置和优化
是不是受够了安装了oracle database之后sqlplus的简陋,无法删除无法上下翻页的苦恼。 可以安装readline和rlwrap插件的话,配置.bahs_profile后也能解决上下翻页这些,但是很多生产环境无法安装rpm包。 oracle提供了sqlcl免费许可,…...