深度学习 | 入个Pytorch的小门
本文主要参考 1’ 2’ 3
更新:2023 / 3 / 1
深度学习 | 入个Pytorch的小门 - 1. 常见数据操作
- 创建
- 操作
- 算术操作
- 加法
- 索引
- 形状
- 查询形状
- 改变形状
- 广播机制
- 广播条件
- 运算
- 数据类型转换
- Tensor转NumPy
- NumPy转Tensor
- 线性回归
- 线性回归的基本要素
- 1. 模型
- 2. 数据集
- 3. 损失函数
- 4. 优化函数 - 随机梯度下降
- 线性回归模型从零开始的实现
- 数据集
- 生成数据集
- 读取数据集
- 初始化模型参数
- 定义模型
- 定义损失函数
- 定义优化函数
- 训练
- 线性回归模型使用pytorch的简洁实现
- 数据集
- 生成数据集
- 读取数据集
- 定义模型
- 初始化模型参数
- 定义损失函数
- 定义优化函数
- 训练
- 多层感知机
- 参考链接
先通过下面的方式确认 Pytorch 已经被正确地安装到你的电脑上,
import torch
torch.manual_seed(0)
torch.cuda.manual_seed(0)print(torch.__version__) // 输出pytorch的版本号
# 1.13.1
创建
- 创建一个
5 x 3的未初始化的Tensor:
tensor1 = torch.empty(5,3)
# tensor([[0.0000e+00, 0.0000e+00, 0.0000e+00],
# [0.0000e+00, 0.0000e+00, -0.0000e+00],
# [0.0000e+00, 0.0000e+00, 0.0000e+00],
# [1.4013e-45, 0.0000e+00, 0.0000e+00],
# [0.0000e+00, 0.0000e+00, 0.0000e+00]])
- 创建一个
5x3的随机初始化的Tensor:
tensor2 = torch.rand(5,3)
# tensor([[0.1898, 0.4211, 0.0858],
# [0.8893, 0.1100, 0.4439],
# [0.3058, 0.6456, 0.3877],
# [0.4485, 0.0570, 0.3891],
# [0.6083, 0.0609, 0.2034]])
- 创建一个
5x3的long型全0的Tensor:
tensor3 = torch.zeros(5,3, dtype=torch.long)
# tensor([[0, 0, 0],
# [0, 0, 0],
# [0, 0, 0],
# [0, 0, 0],
# [0, 0, 0]])
- 直接根据数据创建
tensor4 = torch.tensor([5.5, 3])
# tensor([5.5000, 3.0000])
- 通过现有的
Tensor来创建,此方法会默认重用输入Tensor的一些属性。
tensor5 = torch.zeros(5, 3, dtype=torch.long)
# tensor([[0, 0, 0],
# [0, 0, 0],
# [0, 0, 0],
# [0, 0, 0],
# [0, 0, 0]])
#
# <class 'torch.Tensor'>
#
# torch.int64
#
# cputensor5 = tensor3.new_ones(5, 3, dtype=torch.float64)
# tensor([[1., 1., 1.],
# [1., 1., 1.],
# [1., 1., 1.],
# [1., 1., 1.],
# [1., 1., 1.]], dtype=torch.float64)
#
# <class 'torch.Tensor'>
#
# torch.float64
#
# cputensor5 = torch.randn_like(tensor3, dtype=torch.float)
# tensor([[ 9.8904e-01, 3.8009e-01, -1.5320e-03],
# [-7.3697e-01, -1.6366e+00, -4.0838e-02],
# [-3.4675e-01, 2.5153e+00, 5.3277e-01],
# [-1.5581e+00, 3.5077e-01, 7.3052e-01],
# [-1.9839e+00, 6.9044e-01, 7.0959e-01]])
#
# <class 'torch.Tensor'>
#
# torch.float32
#
# cpu
操作
算术操作
加法
x+y
x = torch.rand(5, 3)
# tensor([[0.3004, 0.9549, 0.5942],
# [0.5424, 0.8032, 0.5955],
# [0.7312, 0.1777, 0.4129],
# [0.3030, 0.4114, 0.8384],
# [0.1771, 0.9954, 0.1406]])y = torch.rand(5, 3)
# tensor([[0.7122, 0.9141, 0.4856],
# [0.7774, 0.5033, 0.6968],
# [0.4215, 0.9920, 0.4468],
# [0.4443, 0.4337, 0.7687],
# [0.1705, 0.5133, 0.2859]])sum = x + y
# tensor([[1.0126, 1.8690, 1.0799],
# [1.3198, 1.3065, 1.2924],
# [1.1527, 1.1697, 0.8597],
# [0.7474, 0.8451, 1.6071],
# [0.3475, 1.5087, 0.4265]])
torch.add(x+y)
x = torch.rand(5, 3)
# tensor([[0.9455, 0.2307, 0.7058],
# [0.1013, 0.2585, 0.1135],
# [0.0834, 0.1876, 0.6470],
# [0.0526, 0.3814, 0.6729],
# [0.5239, 0.7080, 0.2696]])y = torch.rand(5, 3)
# tensor([[0.2314, 0.0348, 0.7387],
# [0.2778, 0.8723, 0.3599],
# [0.8507, 0.5841, 0.0185],
# [0.7318, 0.6347, 0.5771],
# [0.3608, 0.7299, 0.9747]])sum = torch.add(x, y)
# tensor([[1.1768, 0.2655, 1.4445],
# [0.3791, 1.1308, 0.4734],
# [0.9342, 0.7717, 0.6655],
# [0.7844, 1.0161, 1.2500],
# [0.8847, 1.4379, 1.2443]])
或者,
x = torch.rand(5, 3)
# tensor([[0.7198, 0.1457, 0.2093],
# [0.6683, 0.8254, 0.0505],
# [0.8574, 0.1102, 0.5093],
# [0.4496, 0.4313, 0.6737],
# [0.6938, 0.2051, 0.5161]])y = torch.rand(5, 3)
# tensor([[0.2923, 0.7317, 0.6552],
# [0.7680, 0.7655, 0.2276],
# [0.1741, 0.7202, 0.4799],
# [0.0494, 0.8067, 0.1426],
# [0.5097, 0.9381, 0.8655]])result = torch.empty(5, 3)
torch.add(x, y, out=result)
# tensor([[1.0121, 0.8774, 0.8645],
# [1.4363, 1.5909, 0.2781],
# [1.0315, 0.8304, 0.9893],
# [0.4990, 1.2379, 0.8163],
# [1.2035, 1.1432, 1.3816]])
y.add_(x)
x = torch.rand(5, 3)
# tensor([[0.6877, 0.7691, 0.8871],
# [0.4104, 0.2438, 0.4188],
# [0.7285, 0.8033, 0.1320],
# [0.1622, 0.5556, 0.1193],
# [0.6330, 0.6507, 0.2798]])y = torch.rand(5, 3)
# tensor([[0.6695, 0.8028, 0.8364],
# [0.2491, 0.7611, 0.6267],
# [0.5496, 0.1332, 0.4203],
# [0.6156, 0.8650, 0.2299],
# [0.1354, 0.7796, 0.3397]])sum = y.add_(x)
# tensor([[1.3572, 1.5719, 1.7235],
# [0.6595, 1.0049, 1.0454],
# [1.2781, 0.9365, 0.5523],
# [0.7777, 1.4206, 0.3493],
# [0.7683, 1.4303, 0.6195]])
索引
x = torch.rand(5, 3)
# tensor([[0.7302, 0.3153, 0.1036],
# [0.6712, 0.1971, 0.0408],
# [0.4045, 0.8566, 0.6853],
# [0.6205, 0.7717, 0.3650],
# [0.1714, 0.8397, 0.6293]])y = x[0, :] // 引用源tensor的第一行
# tensor([0.7302, 0.3153, 0.1036])
y += 1
# tensor([1.7302, 1.3153, 1.1036])
#
# torch.Size([3])print(x) // # 源tensor也被改了
# tensor([[1.7302, 1.3153, 1.1036],
# [0.6712, 0.1971, 0.0408],
# [0.4045, 0.8566, 0.6853],
# [0.6205, 0.7717, 0.3650],
# [0.1714, 0.8397, 0.6293]])
形状
查询形状
可以通过 shape 或者 size() 来获取 Tensor,比如 tensor1 的形状:
print(tensor1.size())
print(tensor1.shape)
输出为:
torch.Size([5, 3])
torch.Size([5, 3])
注意:返回的 torch.Size 的数据类型是 <class 'torch.Size'>,可以像 tuple 对其进行操作。
改变形状
用 view() 来改变 Tensor 的形状:
x = torch.rand(5, 3)
# tensor([[0.4086, 0.6557, 0.1230],
# [0.0248, 0.0442, 0.0657],
# [0.1682, 0.8937, 0.3877],
# [0.5520, 0.0309, 0.1907],
# [0.0817, 0.9466, 0.7049]])y = x.view(15)
# tensor([0.4086, 0.6557, 0.1230, 0.0248, 0.0442, 0.0657, 0.1682, 0.8937, 0.3877,
# 0.5520, 0.0309, 0.1907, 0.0817, 0.9466, 0.7049])
#
# torch.Size([15])z = x.view(-1, 5)
# tensor([[0.4086, 0.6557, 0.1230, 0.0248, 0.0442],
# [0.0657, 0.1682, 0.8937, 0.3877, 0.5520],
# [0.0309, 0.1907, 0.0817, 0.9466, 0.7049]])
#
# torch.Size([3, 5])
此时如果对 x 操作,y 的值也是会跟着变的,如下所示:
x += 1
# tensor([[1.4086, 1.6557, 1.1230],
# [1.0248, 1.0442, 1.0657],
# [1.1682, 1.8937, 1.3877],
# [1.5520, 1.0309, 1.1907],
# [1.0817, 1.9466, 1.7049]])print(y)
# tensor([1.4086, 1.6557, 1.1230, 1.0248, 1.0442, 1.0657, 1.1682, 1.8937, 1.3877,
# 1.5520, 1.0309, 1.1907, 1.0817, 1.9466, 1.7049])
如果不想共享内存,推荐先用 clone 创造一个副本然后再使用 view。
x_cp = x.clone().view(15)
# tensor([1.4086, 1.6557, 1.1230, 1.0248, 1.0442, 1.0657, 1.1682, 1.8937, 1.3877,
# 1.5520, 1.0309, 1.1907, 1.0817, 1.9466, 1.7049])x -= 1
# tensor([[0.4086, 0.6557, 0.1230],
# [0.0248, 0.0442, 0.0657],
# [0.1682, 0.8937, 0.3877],
# [0.5520, 0.0309, 0.1907],
# [0.0817, 0.9466, 0.7049]])
广播机制
在 Pytorch 中,两个张量形状不同有时也可以进行运算,这涉及到了 Pytorch 中的广播机制,也就是 Pytorch 会自动扩充两个张量,使两个张量的形状相同,然后再进行运算。
下面具体说明 4’ 5:
广播条件
如果两个张量满足下面两个条件,就可以广播:
- 每个张量都至少有一个维度;
x=torch.empty((0,)) # 不能广播,因为两个张量都必须只有一个维度
y=torch.empty(2,2)
- 对两个张量的维度从后往前处理,维度的大小(这个维度的长度)必须要么相等,要么其中一个为
1,或者其中一个张量后面不存在维度了。
x=torch.empty(5,7,3) # 可以广播,对于相同的形状
y=torch.empty(5,7,3)
x=torch.empty(5,3,4,1)
y=torch.empty( 3,1,1) # 可以广播,倒数第一个维度相等,倒数第二个维度不等但其中一个为1,倒数第三个维度相等;
x=torch.empty(3,2,4,1)
y=torch.empty( 3,1,1) # 不能广播,倒数第一个维度相等,倒数第二个维度不等但其中一个为1,倒数第三个维度不等且无1
运算
如果两个张量 x,y 是可广播的,结果的张量大小按如下方式计算:
- 如果
x和y的维度数量不同,对维度数量少的张量增加新的维度,且维度大小为1,使得两个张量的维度数量相同。 - 对每个维度,结果的维度大小是
x和y的维度大小的最大值。(其实如果某个维度大小不同,那么有一个维度大小肯定是1)
下面举几个例子,
x=torch.empty(5,1,4,1)
y=torch.empty( 3,1,1)
(x+y).size()
# torch.Size([5, 3, 4, 1])x=torch.empty(1)
y=torch.empty(3,1,7)
(x+y).size()
# torch.Size([3, 1, 7])x=torch.empty(5,2,4,1)
y=torch.empty(3,1,1)
(x+y).size()
# RuntimeError: The size of tensor a (2) must match the size of tensor b (3) at non-singleton dimension 1
数据类型转换
Tensor转NumPy
以下面的名为 x 的 tensor 为例,
x = torch.ones(5)
y = x.numpy()print(x)
print(type(x))
# tensor([1., 1., 1., 1., 1.])
# <class 'torch.Tensor'>print(y)
print(type(y))
# [1. 1. 1. 1. 1.]
# <class 'numpy.ndarray'>
下面,开始转换:
x += 1print(x)
print(type(x))
# tensor([2., 2., 2., 2., 2.])
# <class 'torch.Tensor'>print(y)
print(type(y))
# [2. 2. 2. 2. 2.]
# <class 'numpy.ndarray'>y += 1print(x)
print(type(x))
# tensor([3., 3., 3., 3., 3.])
# <class 'torch.Tensor'>print(y)
print(type(y))
# [3. 3. 3. 3. 3.]
# <class 'numpy.ndarray'>
NumPy转Tensor
以下面的名为 x 的 numpy.ndarray 为例,
x = np.ones(5)
y = torch.from_numpy(x)print(x)
print(type(x))
# [1. 1. 1. 1. 1.]
# <class 'numpy.ndarray'>print(y)
print(type(y))
# tensor([1., 1., 1., 1., 1.], dtype=torch.float64)
# <class 'torch.Tensor'>
下面,开始转换,
x += 1print(x)
print(type(x))
# [2. 2. 2. 2. 2.]
# <class 'numpy.ndarray'>print(y)
print(type(y))
# tensor([2., 2., 2., 2., 2.], dtype=torch.float64)
# <class 'torch.Tensor'>y += 1print(x)
print(type(x))
# [3. 3. 3. 3. 3.]
# <class 'numpy.ndarray'>print(y)
print(type(y))
# tensor([3., 3., 3., 3., 3.], dtype=torch.float64)
# <class 'torch.Tensor'>
线性回归
简单的说,线性回归预测是基于某个变量 X (自变量)来预测变量 Y(因变量)的值,当然前提是 X 和 Y 之间存在线性关系。这两个变量之间的线性关系可以用直线表示(称为回归线)6。
线性回归的基本要素
1. 模型
举个预测波士顿房价的例子,这里我们都进行了化简:假设房屋价格只取决于两个因素,即 面积(平方米)和 房龄(年)。
接下来我们希望探索价格与这两个因素的具体关系。线性回归假设输出与各个输入之间是线性关系:

2. 数据集
我们收集一系列的真实数据,例如多栋房屋的真实价格和对应的面积、房龄。我们希望在这个数据集上面来拟合模型参数使模型的预测价格与真实价格的误差达到最小。
在 ML 术语中,数据集被称为 训练集( training set ),一栋房屋被称为一个样本( sample ),其真实售出价格叫作标签( label ),用来预测标签的两个因素叫作特征( feature )。
3. 损失函数
在模型训练中,我们需要计算价格预测值与真实值之间的误差。一个常用的选择是平方函数。它在评估索引为的样本误差的表达式为:

4. 优化函数 - 随机梯度下降
当模型和损失函数形式较为简单时,误差最小化问题的解可以直接用公式表达出来,这类解叫作 解析解( analytical solution )。
本节使用的线性回归和平方误差刚好属于这个范畴。
还有一类模型并没有解析解,只能通过优化算法有限次迭代来尽可能降低损失函数的值。这类解叫作 数值解( numerical solution )。
求数值解的优化算法中,小批量随机梯度下降( mini-batch stochastic gradient descent )在深度学习中被广泛使用。先初始化模型参数的初始值;然后对参数进行多次迭代,使每次迭代都降低损失函数的值。
在每次迭代中,先随机均匀采样一个由固定数目训练数据样本所组成的小批量( mini-batch ),然后求小批量中数据样本的平均损失有关模型参数的导数(梯度),最后用此结果与预先设定的一个正数的乘积作为模型参数在本次迭代的减小量。

学习率:代表在每次优化中,能够学习的步长的大小
批量大小:是小批量计算中的批量大小 batch size
线性回归模型从零开始的实现
数据集
生成数据集
使用线性模型来生成数据集,生成一个 1000 个样本的数据集,下面是用来生成数据的线性关系:

import torch
from matplotlib import pyplot as plt
import numpy as np
import random# set input feature number: 1. 'area'; 2. 'age';
num_inputs = 2# set example number: 1000 sample, or, 1000 prices;
num_examples = 1000# set true weight and bias in order to generate corresponded label:
# 1. 'Warea' & 'Wage';
# 2. 'b';
true_w = [2, -3.4]
true_b = 4.2# generate a area and age tensor with torch.Size([1000, 2]);
features = torch.randn(num_examples, num_inputs, dtype=torch.float32)
# tensor([[-1.2659, 1.3218],
# [-1.3461, -0.3002],
# [ 0.6401, 2.2983],
# ...,
# [-0.5203, 0.5586],
# [ 0.0712, -0.3995],
# [-0.2995, 1.1682]])# generate 1000 samples, following the model below:
# price = Warea * area + Wage * age + b
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
# tensor([-2.8260e+00, 2.5284e+00, -2.3339e+00, 3.1779e+00, 2.3752e+00,
# 1.4073e+01, 2.1673e+00, 8.4260e-01, 7.1728e+00, -7.0487e-01,
# ...
# 3.1599e+00, 1.0972e+01, 1.4133e+01, 5.6141e+00, 6.6164e+00,
# 3.2544e+00, 3.9535e+00, 1.2600e+00, 5.7006e+00, -3.7077e-01])# generate a random seed array with (1000, ) size;
seeds = np.random.normal(0, 0.01, size=labels.size())
# [ 8.88058964e-03 3.53739524e-03 7.70576446e-03 -7.14245925e-03
# -6.22237319e-03 1.07257943e-02 4.48531221e-03 -3.44305054e-03
# ...
# - 6.88459456e-03 4.02737440e-03 - 1.95810746e-03 - 7.32376821e-03
# 3.46941304e-03 2.14670627e-03 1.32788726e-02 1.40899248e-02]# apply seed array on previously generated labels tensor;
labels += torch.tensor(seeds, dtype=torch.float32)
# tensor([-2.8172e+00, 2.5319e+00, -2.3262e+00, 3.1708e+00, 2.3690e+00,
# 1.4084e+01, 2.1717e+00, 8.3915e-01, 7.1672e+00, -7.0108e-01,
# ...
# 3.1597e+00, 1.0975e+01, 1.4126e+01, 5.6181e+00, 6.6144e+00,
# 3.2471e+00, 3.9570e+00, 1.2621e+00, 5.7139e+00, -3.5668e-01])
使用 散点图 来呈现上面所生成的数据,如下所示:
# plot with age as x, price as y
plt.scatter(features[:, 1].numpy(), labels.numpy(), 1)
plt.show()

读取数据集
def data_iter(batch_size, features, labels):''':param batch_size: size for a batch of data;:param features: an area and age tensor with torch.Size([1000, 2]);:param labels: price;:return:'''num_examples = len(features) # 1000个samples对应1000组featuresindices = list(range(num_examples)) # 1000个samples的初始索引值为[0, 1, ..., 998, 999]random.shuffle(indices) # 1000个samples的索引值被打乱后为[19, 711, ..., 796, 684, 708, 929, 721, 479, 864, 722, 548, 23]for i in range(0, num_examples, batch_size): # 在indices的列表范围中按序每次抽取10个索引值j = torch.LongTensor(indices[i: min(i + batch_size, num_examples)]) # the last time may be not enough for a whole batch# 最后一组被抽取到的10个索引值所组成的张量组为tensor([796, 684, 708, 929, 721, 479, 864, 722, 548, 23]),数据类型为<class 'torch.Tensor'>,张量大小为torch.Size([10])yield features.index_select(0, j), labels.index_select(0, j)# 按照最后一组10个索引值,对features和labels这两个张量进行索引匹配,所得到的张量如下,大小分别为torch.Size([10, 2]) torch.Size([10])# tensor([[1.6381, 0.5704],# [0.0539, -0.4795],# [-0.2489, 0.3873],# [-0.2030, 0.7919],# [0.6328, 0.8435],# [0.1003, -0.2580],# [0.6470, 1.7876],# [0.6788, -1.7129],# [0.6362, -1.2819],# [0.5954, -1.0731]])# tensor([5.5395, 5.9433, 2.3960, 1.1101, 2.6187, 5.2781, -0.5657, 11.3878,# 9.8319, 9.0328])batch_size = 10
for X, y in data_iter(batch_size, features, labels):print(X, '\n', y)
indices 是 1000 个 sample 值的索引序列。
先使用 random.shuffle 将索引序列 indices 打乱,然后在 [0, 1000] 这个范围内每 10 个为一组对被打乱的 indices 进行按序抽取。再根据抽取到的 10 个索引值,对 features 和 labels 这两个 tensor 进行按索引值进行映射,生成 features.index_select(0, j) 和 labels.index_select(0, j)。
初始化模型参数
num_inputs = 2w = torch.tensor(np.random.normal(0, 0.01, (num_inputs, 1)), dtype=torch.float32)
# tensor([[-0.0064],
# [-0.0057]])
# torch.Size([2, 1])b = torch.zeros(1, dtype=torch.float32)
# tensor([0.])
# torch.Size([1])w.requires_grad_(requires_grad=True)
# tensor([[-0.0064],
# [-0.0057]], requires_grad=True)
# torch.Size([2, 1])b.requires_grad_(requires_grad=True)
# tensor([0.], requires_grad=True)
# torch.Size([1])
通过 num_inputs 确定 features 有 2 个。再通过 require_grad=True 7’ 8 表示需要计算 Tensor 的梯度,告诉自动求导开始记录对 Tensor 的操作。
requires_grad=False可以用来冻结部分网络,只更新另一部分网络的参数。
定义模型
定义用来训练参数的训练模型:
def linreg(X, w, b): return torch.mm(X, w) + b
定义损失函数
我们使用的是 均方误差损失 函数,如下所示:

def squared_loss(y_hat, y): return (y_hat - y.view(y_hat.size())) ** 2 / 2
定义优化函数
在这里优化函数使用的是 小批量随机梯度下降:
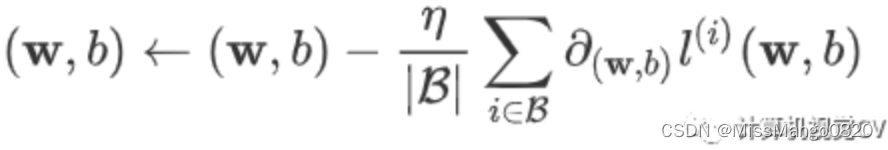
def sgd(params, lr, batch_size): for param in params:param.data -= lr * param.grad / batch_size
训练
lr = 0.03
num_epochs = 5 # 定义训练次数net = linreg # 初始化模型
loss = squared_loss # 初始化损失函数# 开始训练
for epoch in range(num_epochs): # 在每次训练中,dataset中的所有samples只呗使用一次for X, y in data_iter(batch_size, features, labels): # X代表小批量数据中的features, y代表小批量数据中的labelsl = loss(net(X, w, b), y).sum() # 计算小批量数据损失的gradientl.backward()sgd([w, b], lr, batch_size) # 使用w和b来迭代模型中的参数w.grad.data.zero_() # 将模型参数的gradient重置为0b.grad.data.zero_()train_l = loss(net(features, w, b), labels)print('epoch %d, loss %f' % (epoch + 1, train_l.mean().item()))
# epoch 1, loss 0.026009
# epoch 2, loss 0.000095
# epoch 3, loss 0.000049
# epoch 4, loss 0.000049
# epoch 5, loss 0.000049
线性回归模型使用pytorch的简洁实现
数据集
生成数据集
import torch
from torch import nn
import numpy as nptorch.manual_seed(1) # 设置CPU生成随机数的种子,方便下次复现
torch.set_default_tensor_type('torch.FloatTensor') # 设置pytorch中默认的浮点类型num_inputs = 2
num_examples = 1000true_w = [2, -3.4]
true_b = 4.2features = torch.randn(num_examples, num_inputs, dtype=torch.float32)# price = Warea * area + Wage * age + b
labels = true_w[0] * features[:, 0] + true_w[1] * features[:, 1] + true_b
seeds = np.random.normal(0, 0.01, size=labels.size())
labels += torch.tensor(seeds, dtype=torch.float32)
在这里,生成数据集 跟 线性回归模型从零开始的实现 的 生成数据集 的实现中是完全一样的。
torch.manual_seed() 的用法参考此处 9,主要用在随机函数前设置 CPU 生成随机数的种子,确保每次运行随机函数生成的结果都一样,方便下次复现实验结果。
torch.set_default_tensor_type() 的用法参考此处 10,主要用来设置 pytorch 中默认的浮点类型。
读取数据集
import torch.utils.data as Databatch_size = 10# combine features and labels of dataset
dataset = Data.TensorDataset(features, labels)
print(type(dataset))
# <class 'torch.utils.data.dataset.TensorDataset'>
print(dataset.__len__())
# 1000# put dataset into DataLoader
data_iter = Data.DataLoader(dataset=dataset, # torch TensorDataset formatbatch_size=batch_size, # mini batch sizeshuffle=True, # whether shuffle the data or notnum_workers=4, # read data in multithreading
)
print(type(data_iter))
# <class 'torch.utils.data.dataloader.DataLoader'>
print(data_iter.batch_size)
# 10if __name__ == '__main__':for x, y in data_iter:print(x, '\n', y)# tensor([[0.0191, 1.6940],# [-0.7821, -1.4237],# [-1.3451, -0.9675],# [2.0441, -1.3229],# [0.2044, 0.1639],# [0.2546, -0.5020],# [-1.2512, -0.2749],# [-0.2890, 0.1522],# [0.1878, 0.2935],# [0.0353, -0.3365]])# tensor([-1.5019, 7.4767, 4.7906, 12.7802, 4.0670, 6.4010, 2.6281, 3.1145,# 3.5805, 5.4059])print(x.shape, y.shape)# torch.Size([10, 2])# torch.Size([10])break
Data.DataLoader 的用法可以参考这里 11’ 12’ 13。
定义模型
from torch import nnclass LinearNet(nn.Module):def __init__(self, n_feature):super(LinearNet, self).__init__() # call father function to initself.linear = nn.Linear(n_feature, 1) # function prototype: `torch.nn.Linear(in_features, out_features, bias=True)`def forward(self, x):y = self.linear(x)return ynet = LinearNet(num_inputs)# ways to init a multilayer network# method Nr.1
net = nn.Sequential(nn.Linear(num_inputs, 1)# other layers can be added here
)# method Nr.2
net = nn.Sequential()
net.add_module('linear', nn.Linear(num_inputs, 1))
# net.add_module ......# method Nr.3
from collections import OrderedDict
net = nn.Sequential(OrderedDict([('linear', nn.Linear(num_inputs, 1))# ......
])
)
初始化模型参数
from torch.nn import initinit.normal_(net[0].weight, mean=0.0, std=0.01)
init.constant_(net[0].bias, val=0.0) # or you can use `net[0].bias.data.fill_(0)` to modify it directlyfor param in net.parameters():print(param)
# Parameter
# containing:
# tensor([[0.0044, -0.0017]], requires_grad=True)
#
# Parameter
# containing:
# tensor([0.], requires_grad=True)
定义损失函数
loss = nn.MSELoss() # nn built-in squared loss function# function prototype: `torch.nn.MSELoss(size_average=None, reduce=None, reduction='mean')`print(loss)
# MSELoss()print(type(loss))
# <class 'torch.nn.modules.loss.MSELoss'>
定义优化函数
import torch.optim as optimoptimizer = optim.SGD(net.parameters(), lr=0.03) # built-in random gradient descent function# function prototype: `torch.optim.SGD(params, lr=, momentum=0, dampening=0, weight_decay=0, nesterov=False)`
print(optimizer)
# SGD(
# Parameter
# Group
# 0
# dampening: 0
# differentiable: False
# foreach: None
# lr: 0.03
# maximize: False
# momentum: 0
# nesterov: False
# weight_decay: 0
# )print(type(optimizer))
# <class 'torch.optim.sgd.SGD'>
训练
num_epochs = 3
for epoch in range(1, num_epochs + 1):for X, y in data_iter:output = net(X)l = loss(output, y.view(-1, 1))optimizer.zero_grad() # reset gradient, equal to net.zero_grad()l.backward()optimizer.step()print('epoch %d, loss: %f' % (epoch, l.item()))
# epoch 1, loss: 0.000148
# epoch 2, loss: 0.000210
# epoch 3, loss: 0.000216
先后进行三次训练,得到每次的样本误差。
然后对用于生成数据集的 weight 和 bias 和经过训练计算而得到的 weight 和 bias 进行对比,如下所示:
# result comparision
dense = net[0]
print(f"weight:\n{true_w} V.S {dense.weight.data}")
print(f"bias:\n{true_b} V.S {dense.bias.data}")
# weight:
# [2, -3.4] V.S tensor([[ 1.9996, -3.3998]])
# bias:
# 4.2 V.S tensor([4.2004])
多层感知机
参考这里 14
参考链接
从零开始学Pytorch ↩︎
从零开始学Pytorch(一)之常见数据操作 ↩︎
PyTorch中文文档 ↩︎
pytorch中的广播机制 ↩︎
Pytorch中的广播机制 ↩︎
从零开始学Pytorch(二)之线性回归 ↩︎
Pytorch中requires_grad_(), detach(), torch.no_grad()的区别 ↩︎
TORCH.TENSOR.REQUIRES_GRAD_ ↩︎
【pytorch】torch.manual_seed()用法详解 ↩︎
pytorch每日一学8(torch.set_default_tensor_type(t)) ↩︎
RuntimeError: DataLoader worker (pid(s) 9528, 8320) exited unexpectedly ↩︎
RuntimeError: DataLoader worker exited unexpectedly ↩︎
pytorch-Dataloader多进程使用出错 ↩︎
从零开始学Pytorch(三)之多层感知机的实现 ↩︎
相关文章:
深度学习 | 入个Pytorch的小门
本文主要参考 1’ 2’ 3 更新:2023 / 3 / 1 深度学习 | 入个Pytorch的小门 - 1. 常见数据操作创建操作算术操作加法索引形状查询形状改变形状广播机制广播条件运算数据类型转换Tensor转NumPyNumPy转Tensor线性回归线性回归的基本要素1. 模型2. 数据集3. 损失函数4.…...

应用上云指导
应用上云指导方法论。应用上云指传统应用迁移到云上,云上应用采用K8S部署。本文旨在提供一种方法、流程,指导应用上云,以求优化上云工作,提供应用上云效率。主要包含以下内容:应用上云工作角色、分工应用上云标准流程及…...

进程概念~
进程概念 (冯诺依曼体系结构,操作系统,进程概念,进程状态,环境变量,程序地址空间) 冯诺依曼体系结构:(计算机硬件体系结构) 输入设备,输出设备&a…...

三天吃透Java基础八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...
YOLOv8训练自己的数据集(超详细)
一、准备深度学习环境本人的笔记本电脑系统是:Windows10YOLO系列最新版本的YOLOv8已经发布了,详细介绍可以参考我前面写的博客,目前ultralytics已经发布了部分代码以及说明,可以在github上下载YOLOv8代码,代码文件夹中…...
)
【洛谷 P1088】[NOIP2004 普及组] 火星人 题解(全排列+向量)
[NOIP2004 普及组] 火星人 题目描述 人类终于登上了火星的土地并且见到了神秘的火星人。人类和火星人都无法理解对方的语言,但是我们的科学家发明了一种用数字交流的方法。这种交流方法是这样的,首先,火星人把一个非常大的数字告诉人类科学…...

基于混合蛙跳算法优化SVM的滚动轴承故障诊断python实现
1.混合蛙跳算法(SFLA)原理 混合蛙跳算法(SFLA)是一种受自然生物模仿启示而产生的基于群体的协同搜索方法,由局部搜索和全局信息交换两部分组成。 混合蛙跳算法中,每个青蛙的位置代表了一个可行解。青蛙在沼泽中跳跃,沼泽在离散的地方有很多石头,青蛙可以跳过这些石头来找…...

如何让AI帮你干活-娱乐(2)
背景:好容易完成朋友的任务,帮忙给小朋友绘画比赛生成一些创意参考图片。他给我个挑战更高的问题,是否可以帮他用AI生成一些视频。这个乍一听以现在AI技术根本不太可能完成。奈何他各种坚持,无奈被迫营业。苦脸接受了这个不可能完…...

文件异步多备常用方案
业务需求上经常存在需要对同一个文件进行双上传,上传到不同云存储桶,以防出现某一个云厂商因各种意外导致自身服务出现不可用的情况,当然,还有其他措施可以避免,现在只针对通过程序业务代码而双写存储的这个场景。 业务…...
java面试八股文之------Redis夺命连环25问
java面试八股文之------Redis夺命连环25问👨🎓1.为什么redis这么快👨🎓2.redis的应用场景,为什么要用👨🎓3.redis6.0之前为什么一直不使用多线程,6.0为甚么又使用多线程了&…...
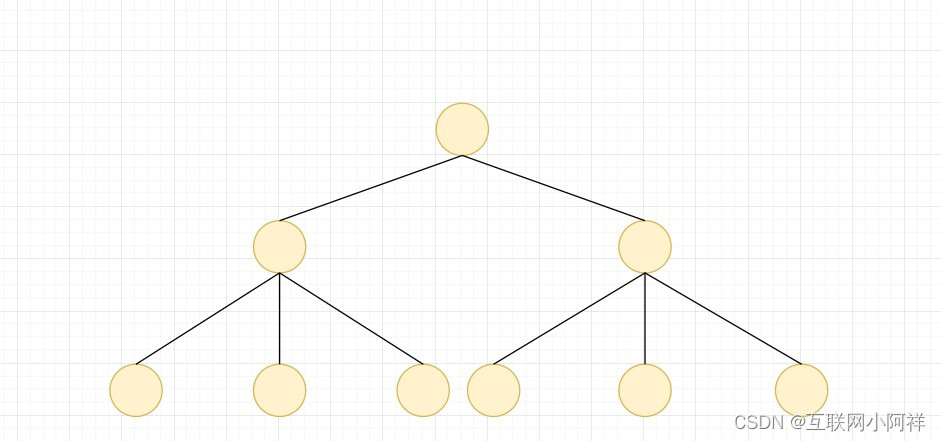
【数据结构】AVL平衡二叉树底层原理以及二叉树的演进之多叉树
1.AVL平衡二叉树底层原理 背景 二叉查找树左右子树极度不平衡,退化成为链表时候,相当于全表扫描,时间复杂度就变为了O(n) 插入速度没影响,但是查询速度变慢,比单链表都慢,每次都要判断左右子树是否为空 需…...

K8S篇-安装nfs插件
前言 有关k8s的搭建可以参考:http://t.csdn.cn/H84Zu 有关过程中使用到的nfs相关的nas,可以参考: http://t.csdn.cn/ACfoT http://t.csdn.cn/tPotK http://t.csdn.cn/JIn27 安装nfs存储插件 NFS-Subdir-External-Provisioner是一个自动配置…...
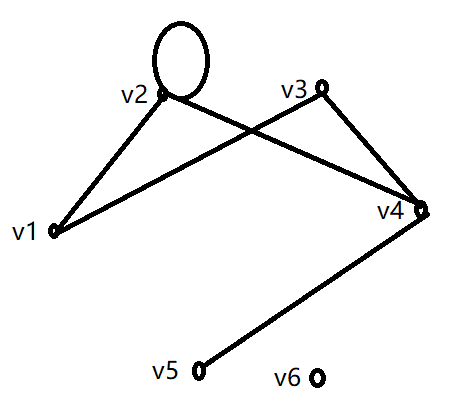
xmu 离散数学 卢杨班作业详解【4-7章】
文章目录第四章 二元关系和函数4.6.2911121618.120.222.1232834第五章 代数系统的一般概念2判断二元运算是否封闭348111214第六章 几个典型的代数系统1.5.6.7.11.12151618第七章 图的基本概念12479111215第四章 二元关系和函数 4. A{1,2,3} 恒等关系 IA{<1,1>,<2,2…...

多重背包问题中的二进制状态压缩
1.多重背包问题 经典的多重背包问题和01背包问题的相似之处在于二者的一维遍历顺序都是从右侧往左侧遍历。 同时多重背包的一维写法不比二维写法降低时间复杂度。 2.多重背包标准写法:(平铺展开形式) class Solution {public int maxValue(int N, int C, int[] s…...

汇编语言程序设计(四)之汇编指令
系列文章 汇编语言程序设计(一) 汇编语言程序设计(二)之寄存器 汇编语言程序设计(三)之汇编程序 汇编指令 1. 数据传输指令 指令包括:MOV、XCHG、XLAT、LEA、LDS、LES、PUSH、POP、PUSHF、LA…...

Vant2 源码分析之 vant-sticky
前言 原打算借鉴 vant-sticky 源码,实现业务需求的某个功能,第一眼看以为看懂了,拿来用的时候,才发现一知半解。看第二遍时,对不起,是我肤浅了。这里侧重分析实现原理,其他部分不拓展开来&…...
【自然语言处理】【大模型】大语言模型BLOOM推理工具测试
相关博客 【自然语言处理】【大模型】大语言模型BLOOM推理工具测试 【自然语言处理】【大模型】GLM-130B:一个开源双语预训练语言模型 【自然语言处理】【大模型】用于大型Transformer的8-bit矩阵乘法介绍 【自然语言处理】【大模型】BLOOM:一个176B参数…...
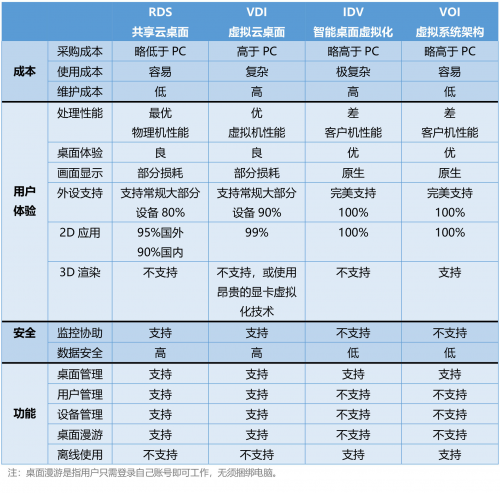
云桌面技术初识:VDI,IDV,VOI,RDS
VDI(Virtual Desktop Infrastucture,虚拟桌面架构),俗称虚拟云桌面 VDI构架采用的“集中存储、集中运算”构架,所有的桌面以虚拟机的方式运行在服务器硬件虚拟化层上,桌面以图像传输的方式发送到客户端。 …...

基于本地centos构建gdal2.4.4镜像
1.前言 基于基础镜像构建gdal环境一般特别大,一般少则1.6G,多则2G甚至更大,这对于镜像的迁移造成了极大的不便。究其原因在于容器中有大量的源码文件以及编译中间过程文件,还要大量编译需要的yum库。本文主要通过在centos系统上先…...

生产环境线程问题排查
线程状态的解读RUNNABLE线程处于运行状态,不一定消耗CPU。例如,线程从网络读取数据,大多数时间是挂起的,只有数据到达时才会重新唤起进入执行状态。只有Java代码显式调用sleep或wait方法时,虚拟机才可以精准获取到线程…...

【大模型RAG】拍照搜题技术架构速览:三层管道、两级检索、兜底大模型
摘要 拍照搜题系统采用“三层管道(多模态 OCR → 语义检索 → 答案渲染)、两级检索(倒排 BM25 向量 HNSW)并以大语言模型兜底”的整体框架: 多模态 OCR 层 将题目图片经过超分、去噪、倾斜校正后,分别用…...

《Playwright:微软的自动化测试工具详解》
Playwright 简介:声明内容来自网络,将内容拼接整理出来的文档 Playwright 是微软开发的自动化测试工具,支持 Chrome、Firefox、Safari 等主流浏览器,提供多语言 API(Python、JavaScript、Java、.NET)。它的特点包括&a…...

线程与协程
1. 线程与协程 1.1. “函数调用级别”的切换、上下文切换 1. 函数调用级别的切换 “函数调用级别的切换”是指:像函数调用/返回一样轻量地完成任务切换。 举例说明: 当你在程序中写一个函数调用: funcA() 然后 funcA 执行完后返回&…...

Leetcode 3577. Count the Number of Computer Unlocking Permutations
Leetcode 3577. Count the Number of Computer Unlocking Permutations 1. 解题思路2. 代码实现 题目链接:3577. Count the Number of Computer Unlocking Permutations 1. 解题思路 这一题其实就是一个脑筋急转弯,要想要能够将所有的电脑解锁&#x…...

Python爬虫(一):爬虫伪装
一、网站防爬机制概述 在当今互联网环境中,具有一定规模或盈利性质的网站几乎都实施了各种防爬措施。这些措施主要分为两大类: 身份验证机制:直接将未经授权的爬虫阻挡在外反爬技术体系:通过各种技术手段增加爬虫获取数据的难度…...

Axios请求超时重发机制
Axios 超时重新请求实现方案 在 Axios 中实现超时重新请求可以通过以下几种方式: 1. 使用拦截器实现自动重试 import axios from axios;// 创建axios实例 const instance axios.create();// 设置超时时间 instance.defaults.timeout 5000;// 最大重试次数 cons…...

浅谈不同二分算法的查找情况
二分算法原理比较简单,但是实际的算法模板却有很多,这一切都源于二分查找问题中的复杂情况和二分算法的边界处理,以下是博主对一些二分算法查找的情况分析。 需要说明的是,以下二分算法都是基于有序序列为升序有序的情况…...

Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信
文章目录 Linux C语言网络编程详细入门教程:如何一步步实现TCP服务端与客户端通信前言一、网络通信基础概念二、服务端与客户端的完整流程图解三、每一步的详细讲解和代码示例1. 创建Socket(服务端和客户端都要)2. 绑定本地地址和端口&#x…...

AirSim/Cosys-AirSim 游戏开发(四)外部固定位置监控相机
这个博客介绍了如何通过 settings.json 文件添加一个无人机外的 固定位置监控相机,因为在使用过程中发现 Airsim 对外部监控相机的描述模糊,而 Cosys-Airsim 在官方文档中没有提供外部监控相机设置,最后在源码示例中找到了,所以感…...

C/C++ 中附加包含目录、附加库目录与附加依赖项详解
在 C/C 编程的编译和链接过程中,附加包含目录、附加库目录和附加依赖项是三个至关重要的设置,它们相互配合,确保程序能够正确引用外部资源并顺利构建。虽然在学习过程中,这些概念容易让人混淆,但深入理解它们的作用和联…...
