【剑指Offer-Java】包含min函数的栈?
题目
定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。
MinStack minStack = new MinStack();
minStack.push(-2);
minStack.push(0);
minStack.push(-3);
minStack.min(); --> 返回 -3.
minStack.pop();
minStack.top(); --> 返回 0.
minStack.min(); --> 返回 -2.
提示:
各函数的调用总次数不超过 20000 次
实现
- 函数调用次数限制,因此min不能直接遍历大小,选择用两个栈,栈B用于存储较小数,严格降序排列。
- 直到A空,B才为空!
class MinStack {Stack<Integer> A, B;public MinStack() {A = new Stack<>();#栈 B = new Stack<>();}public void push(int x) {A.add(x);if(B.empty() || B.peek() >= x)B.add(x);}public void pop() {if(A.pop().equals(B.peek()))B.pop();}public int top() {return A.peek();}public int min() {return B.peek();}
}
总结
- Stack
- add(x)
- peek()
- pop()
- empty()
相关文章:

【剑指Offer-Java】包含min函数的栈?
题目 定义栈的数据结构,请在该类型中实现一个能够得到栈的最小元素的 min 函数在该栈中,调用 min、push 及 pop 的时间复杂度都是 O(1)。 MinStack minStack new MinStack(); minStack.push(-2); minStack.push(0); minStack.push(-3); minStack.min()…...

红队APT——邮件钓鱼攻击SwaksOffice漏洞RLO隐藏压缩释放
目录 (一)采用自己搭建Ewomail配合Swaks 0x01 搭建过程 0x02 配置转发信息 (二)网页钓鱼-克隆修改...

【Java|基础篇】超详细讲解运算符
文章目录1. 什么是运算符2. 算术运算符隐式类型转换强制类型转换字符串的拼接字符相加自增和自减运算符3.赋值运算符4. 关系运算符5. 逻辑运算符短路与(&&)和短路或(||)6.三目运算符7. 位运算符8. 移位运算1. 什么是运算符 运算符用于执行程序代码运算,会针…...
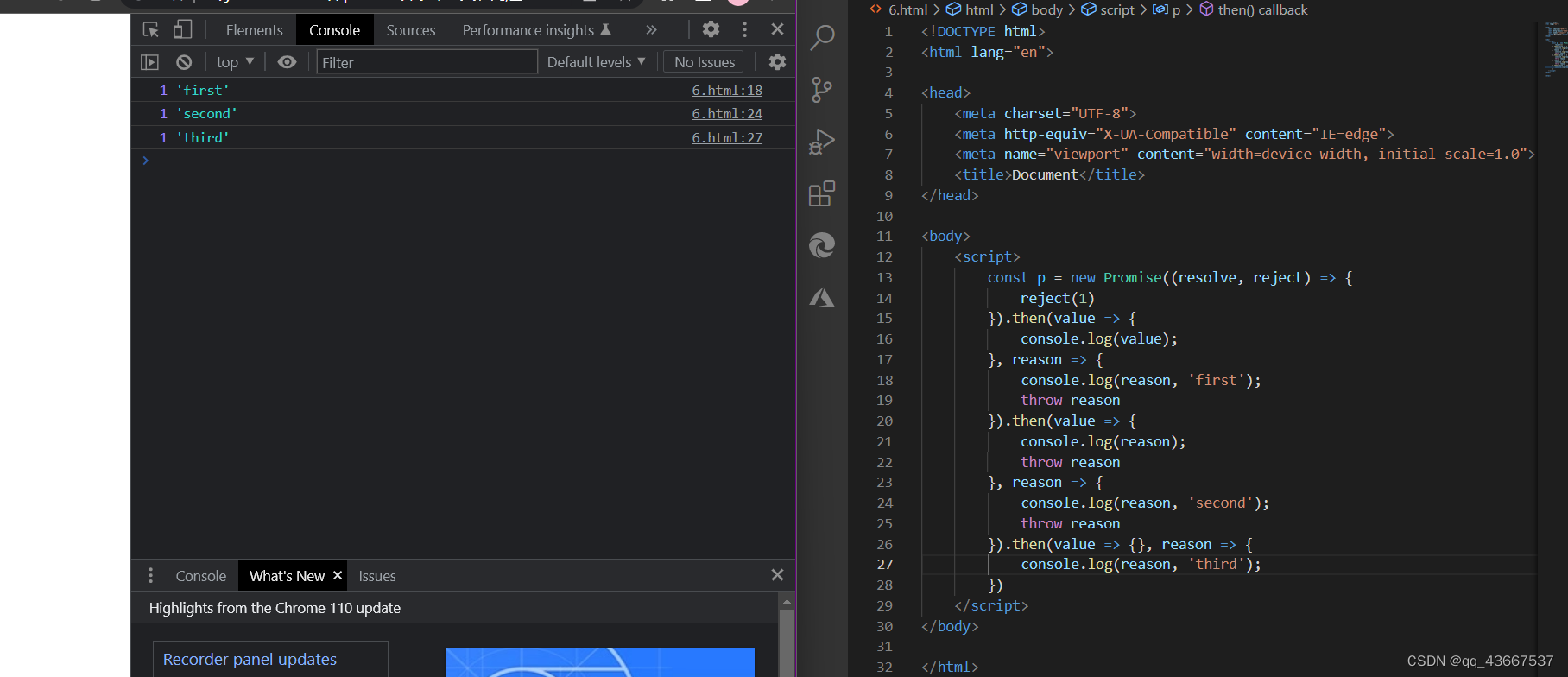
Promise-异步回调
1.理解Promise promise是ES6提出的异步编程的新的解决方案,通过链式调用解决ajax回调地狱 从语法上看,promise是一个构造函数,自己身上有all、reject、resolve方法,原型上有then、catch方法 从功能上看,Promise对象用…...

【设计模式之美 设计原则与思想:设计原则】21 | 理论七:重复的代码就一定违背DRY吗?如何提高代码的复用性?
在上一节课中,我们讲了 KISS 原则和 YAGNI 原则,KISS 原则可以说是人尽皆知。今天,我们再学习一个你肯定听过的原则,那就是 DRY 原则。它的英文描述为:Don’t Repeat Yourself。中文直译为:不要重复自己。将…...
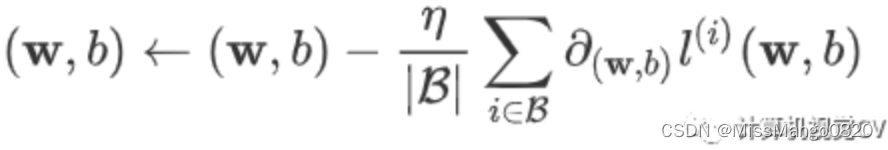
深度学习 | 入个Pytorch的小门
本文主要参考 1’ 2’ 3 更新:2023 / 3 / 1 深度学习 | 入个Pytorch的小门 - 1. 常见数据操作创建操作算术操作加法索引形状查询形状改变形状广播机制广播条件运算数据类型转换Tensor转NumPyNumPy转Tensor线性回归线性回归的基本要素1. 模型2. 数据集3. 损失函数4.…...

应用上云指导
应用上云指导方法论。应用上云指传统应用迁移到云上,云上应用采用K8S部署。本文旨在提供一种方法、流程,指导应用上云,以求优化上云工作,提供应用上云效率。主要包含以下内容:应用上云工作角色、分工应用上云标准流程及…...

进程概念~
进程概念 (冯诺依曼体系结构,操作系统,进程概念,进程状态,环境变量,程序地址空间) 冯诺依曼体系结构:(计算机硬件体系结构) 输入设备,输出设备&a…...

三天吃透Java基础八股文
本文已经收录到Github仓库,该仓库包含计算机基础、Java基础、多线程、JVM、数据库、Redis、Spring、Mybatis、SpringMVC、SpringBoot、分布式、微服务、设计模式、架构、校招社招分享等核心知识点,欢迎star~ Github地址:https://github.com/…...
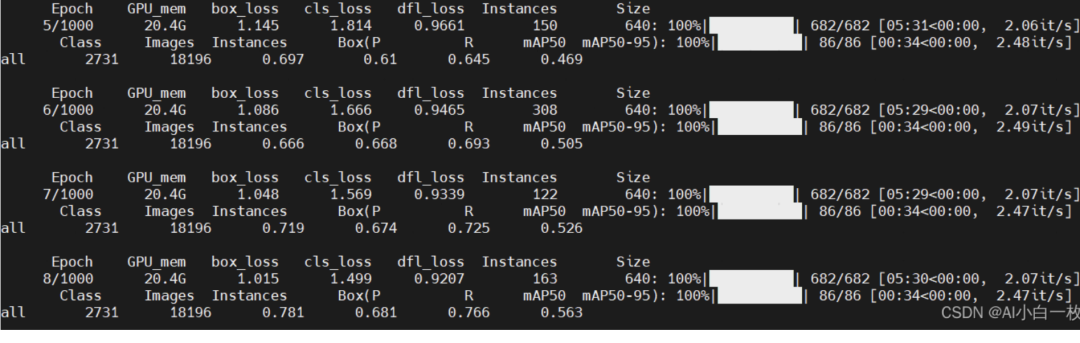
YOLOv8训练自己的数据集(超详细)
一、准备深度学习环境本人的笔记本电脑系统是:Windows10YOLO系列最新版本的YOLOv8已经发布了,详细介绍可以参考我前面写的博客,目前ultralytics已经发布了部分代码以及说明,可以在github上下载YOLOv8代码,代码文件夹中…...
)
【洛谷 P1088】[NOIP2004 普及组] 火星人 题解(全排列+向量)
[NOIP2004 普及组] 火星人 题目描述 人类终于登上了火星的土地并且见到了神秘的火星人。人类和火星人都无法理解对方的语言,但是我们的科学家发明了一种用数字交流的方法。这种交流方法是这样的,首先,火星人把一个非常大的数字告诉人类科学…...

基于混合蛙跳算法优化SVM的滚动轴承故障诊断python实现
1.混合蛙跳算法(SFLA)原理 混合蛙跳算法(SFLA)是一种受自然生物模仿启示而产生的基于群体的协同搜索方法,由局部搜索和全局信息交换两部分组成。 混合蛙跳算法中,每个青蛙的位置代表了一个可行解。青蛙在沼泽中跳跃,沼泽在离散的地方有很多石头,青蛙可以跳过这些石头来找…...

如何让AI帮你干活-娱乐(2)
背景:好容易完成朋友的任务,帮忙给小朋友绘画比赛生成一些创意参考图片。他给我个挑战更高的问题,是否可以帮他用AI生成一些视频。这个乍一听以现在AI技术根本不太可能完成。奈何他各种坚持,无奈被迫营业。苦脸接受了这个不可能完…...

文件异步多备常用方案
业务需求上经常存在需要对同一个文件进行双上传,上传到不同云存储桶,以防出现某一个云厂商因各种意外导致自身服务出现不可用的情况,当然,还有其他措施可以避免,现在只针对通过程序业务代码而双写存储的这个场景。 业务…...
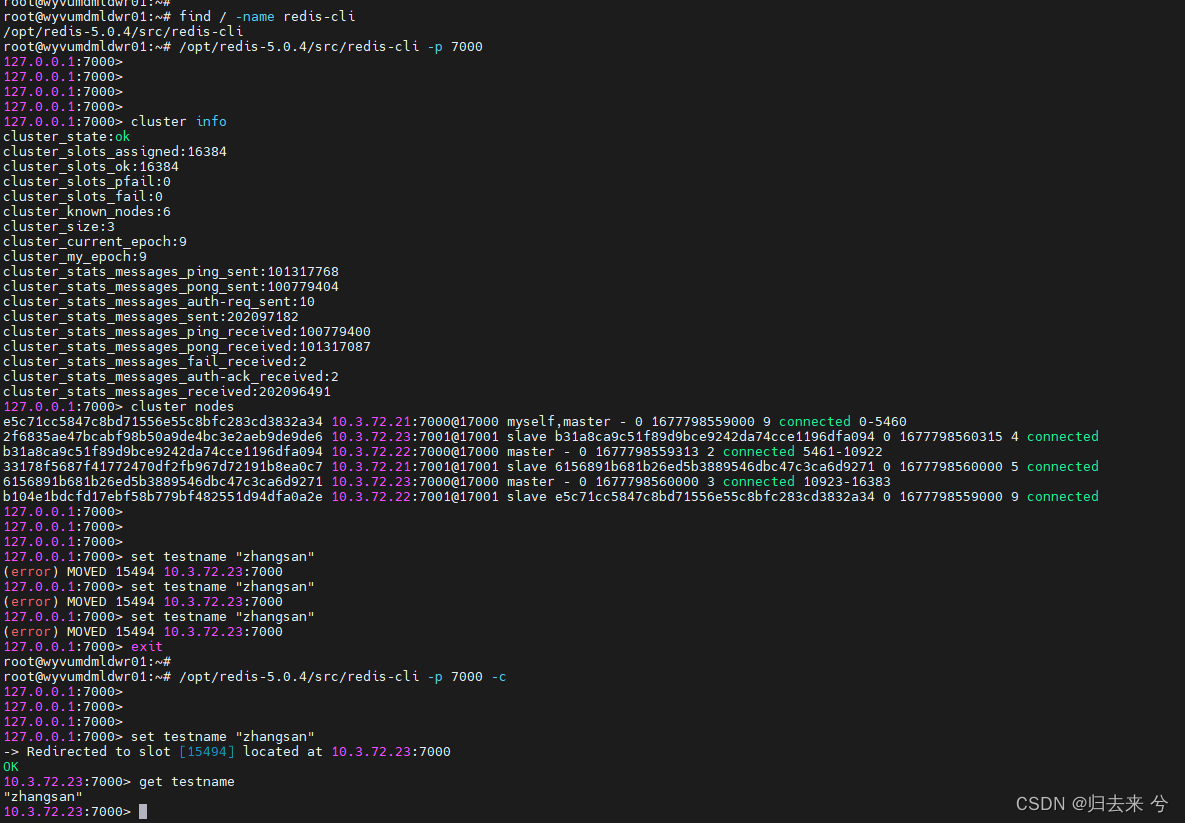
java面试八股文之------Redis夺命连环25问
java面试八股文之------Redis夺命连环25问👨🎓1.为什么redis这么快👨🎓2.redis的应用场景,为什么要用👨🎓3.redis6.0之前为什么一直不使用多线程,6.0为甚么又使用多线程了&…...
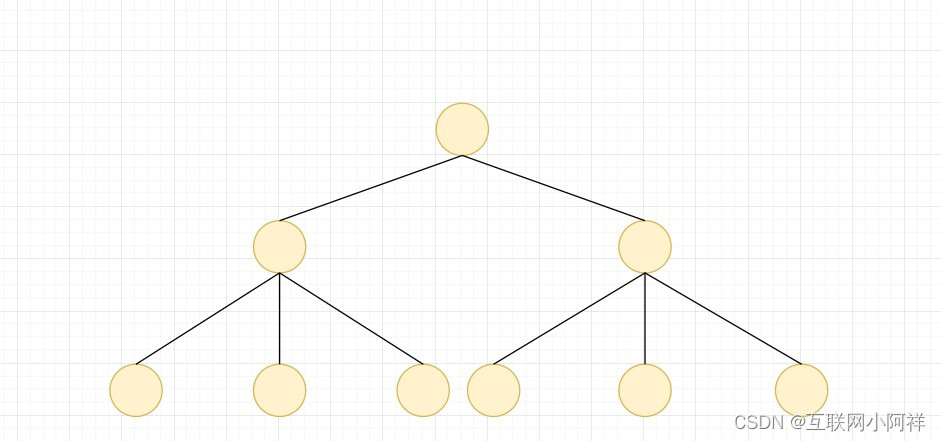
【数据结构】AVL平衡二叉树底层原理以及二叉树的演进之多叉树
1.AVL平衡二叉树底层原理 背景 二叉查找树左右子树极度不平衡,退化成为链表时候,相当于全表扫描,时间复杂度就变为了O(n) 插入速度没影响,但是查询速度变慢,比单链表都慢,每次都要判断左右子树是否为空 需…...

K8S篇-安装nfs插件
前言 有关k8s的搭建可以参考:http://t.csdn.cn/H84Zu 有关过程中使用到的nfs相关的nas,可以参考: http://t.csdn.cn/ACfoT http://t.csdn.cn/tPotK http://t.csdn.cn/JIn27 安装nfs存储插件 NFS-Subdir-External-Provisioner是一个自动配置…...
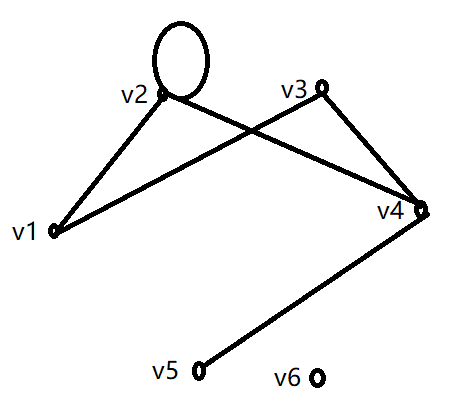
xmu 离散数学 卢杨班作业详解【4-7章】
文章目录第四章 二元关系和函数4.6.2911121618.120.222.1232834第五章 代数系统的一般概念2判断二元运算是否封闭348111214第六章 几个典型的代数系统1.5.6.7.11.12151618第七章 图的基本概念12479111215第四章 二元关系和函数 4. A{1,2,3} 恒等关系 IA{<1,1>,<2,2…...

多重背包问题中的二进制状态压缩
1.多重背包问题 经典的多重背包问题和01背包问题的相似之处在于二者的一维遍历顺序都是从右侧往左侧遍历。 同时多重背包的一维写法不比二维写法降低时间复杂度。 2.多重背包标准写法:(平铺展开形式) class Solution {public int maxValue(int N, int C, int[] s…...

汇编语言程序设计(四)之汇编指令
系列文章 汇编语言程序设计(一) 汇编语言程序设计(二)之寄存器 汇编语言程序设计(三)之汇编程序 汇编指令 1. 数据传输指令 指令包括:MOV、XCHG、XLAT、LEA、LDS、LES、PUSH、POP、PUSHF、LA…...

[特殊字符] 智能合约中的数据是如何在区块链中保持一致的?
🧠 智能合约中的数据是如何在区块链中保持一致的? 为什么所有区块链节点都能得出相同结果?合约调用这么复杂,状态真能保持一致吗?本篇带你从底层视角理解“状态一致性”的真相。 一、智能合约的数据存储在哪里…...

Java 8 Stream API 入门到实践详解
一、告别 for 循环! 传统痛点: Java 8 之前,集合操作离不开冗长的 for 循环和匿名类。例如,过滤列表中的偶数: List<Integer> list Arrays.asList(1, 2, 3, 4, 5); List<Integer> evens new ArrayList…...

ip子接口配置及删除
配置永久生效的子接口,2个IP 都可以登录你这一台服务器。重启不失效。 永久的 [应用] vi /etc/sysconfig/network-scripts/ifcfg-eth0修改文件内内容 TYPE"Ethernet" BOOTPROTO"none" NAME"eth0" DEVICE"eth0" ONBOOT&q…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

华硕a豆14 Air香氛版,美学与科技的馨香融合
在快节奏的现代生活中,我们渴望一个能激发创想、愉悦感官的工作与生活伙伴,它不仅是冰冷的科技工具,更能触动我们内心深处的细腻情感。正是在这样的期许下,华硕a豆14 Air香氛版翩然而至,它以一种前所未有的方式&#x…...

Fabric V2.5 通用溯源系统——增加图片上传与下载功能
fabric-trace项目在发布一年后,部署量已突破1000次,为支持更多场景,现新增支持图片信息上链,本文对图片上传、下载功能代码进行梳理,包含智能合约、后端、前端部分。 一、智能合约修改 为了增加图片信息上链溯源,需要对底层数据结构进行修改,在此对智能合约中的农产品数…...

uniapp 字符包含的相关方法
在uniapp中,如果你想检查一个字符串是否包含另一个子字符串,你可以使用JavaScript中的includes()方法或者indexOf()方法。这两种方法都可以达到目的,但它们在处理方式和返回值上有所不同。 使用includes()方法 includes()方法用于判断一个字…...
)
【LeetCode】3309. 连接二进制表示可形成的最大数值(递归|回溯|位运算)
LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 题目描述解题思路Java代码 题目描述 题目链接:LeetCode 3309. 连接二进制表示可形成的最大数值(中等) 给你一个长度为 3 的整数数组 nums。 现以某种顺序 连接…...

毫米波雷达基础理论(3D+4D)
3D、4D毫米波雷达基础知识及厂商选型 PreView : https://mp.weixin.qq.com/s/bQkju4r6med7I3TBGJI_bQ 1. FMCW毫米波雷达基础知识 主要参考博文: 一文入门汽车毫米波雷达基本原理 :https://mp.weixin.qq.com/s/_EN7A5lKcz2Eh8dLnjE19w 毫米波雷达基础…...

恶补电源:1.电桥
一、元器件的选择 搜索并选择电桥,再multisim中选择FWB,就有各种型号的电桥: 电桥是用来干嘛的呢? 它是一个由四个二极管搭成的“桥梁”形状的电路,用来把交流电(AC)变成直流电(DC)。…...
