【C++】实现红黑树
目录
- 一、认识红黑树
- 1.1 概念
- 1.2 定义
- 二、实现红黑树
- 2.1 插入
- 2.2 与AVL树对比
一、认识红黑树
1.1 概念
红黑树是一个二叉搜索树,与AVL树相比,红黑树不再使用平衡因子来控制树的左右子树高度差,而是用颜色来控制平衡,颜色为红色或者黑色。控制任意一条从根到叶子节点的路径的节点颜色,就可以确保没有一条路径会比其他路径长出俩倍,因而是接近平衡的。

红黑树的规则:
- 根节点是黑色的
- 不能有连续的红色节点
- 从某个节点出发,每条路径上的黑色节点的数量相同
1.2 定义
红黑树也是三叉链结构(左指针、右指针和父亲指针),有一个新的存储位来记录节点的颜色,这里实现的红黑树是kv模型。
enum Colour
{RED,//红色BLACK//黑色
};template<class K, class V>
struct RBTreeNode
{RBTreeNode<K, V>* _left;RBTreeNode<K, V>* _right;RBTreeNode<K, V>* _parent;pair<K, V> _kv;Colour _col;RBTreeNode(const pair<K, V>& kv):_left(nullptr), _right(nullptr), _parent(nullptr),_kv(kv),_col(RED)//默认的新节点都是红色的{}
};
二、实现红黑树
2.1 插入
红黑树的插入的与普通二叉搜索树的插入逻辑是一样的,不同的是插入新节点后要进行变色处理,符合前面的规则才行。
红黑树的插入一共分为两大类:
- 新插入的节点的父节点是黑色的,插入结束
- 新插入的节点的父节点是红色的,要变色处理
也就是说要看新插入的节点的父节点的颜色来确定是否本次插入结束。但是有个问题,新插入的节点说什么颜色的?其实看图就可以知道,插入的新节点必须是红色的,因为如果插入的是黑色节点,那么必然会导致每条路径上的黑色节点数量不相同,违反规则。
接下来看红黑树插入节点时是怎样变色的:
首先按照前面插入的两大类,如果插入节点的父节点是黑色的,就不需要进入变色调整;反之,如果插入节点的父节点存在且是红色的,说明此时有连续的红色节点,要变色处理。
这里需要定义几个节点的名字,方便叙述和画图:
- c(cur)——当前新插入的节点
- p(parent)——插入节点的父节点
- g(grandfather)——父节点的父节点
- u(uncle)——叔叔节点,父节点的另一边的节点
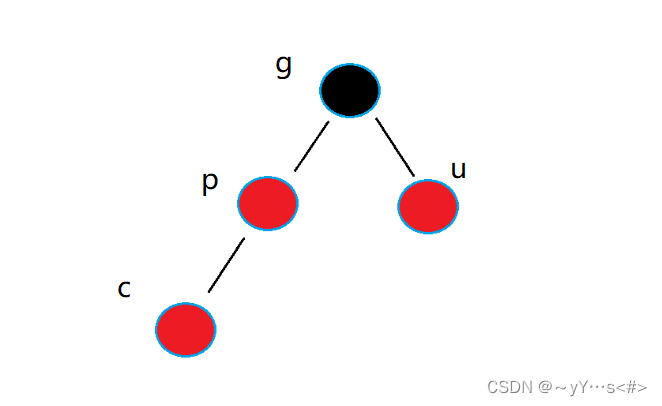
这4个节点主要看叔叔节点,根据叔叔节点分为两种情况。
情况一:叔叔存在且为红
p和u要变成黑色,g变成红色。如果g不是根节点,要向上更新,把g当成c;如果g是根节点,要把g变成黑色的,因为根节点必须是黑的。
1️⃣g是根节点
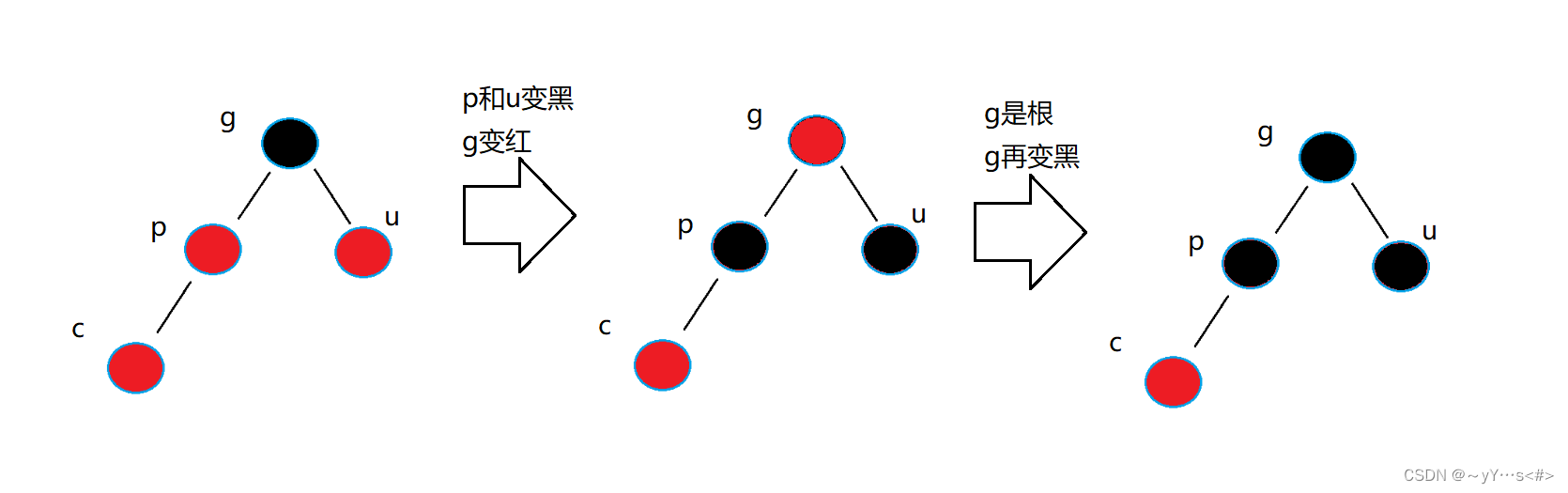
注意:不管p或者u是g的左边还是右边都是一样的,c在p的左边/右边都是一样的操作,不影响。
2️⃣g不是根节点
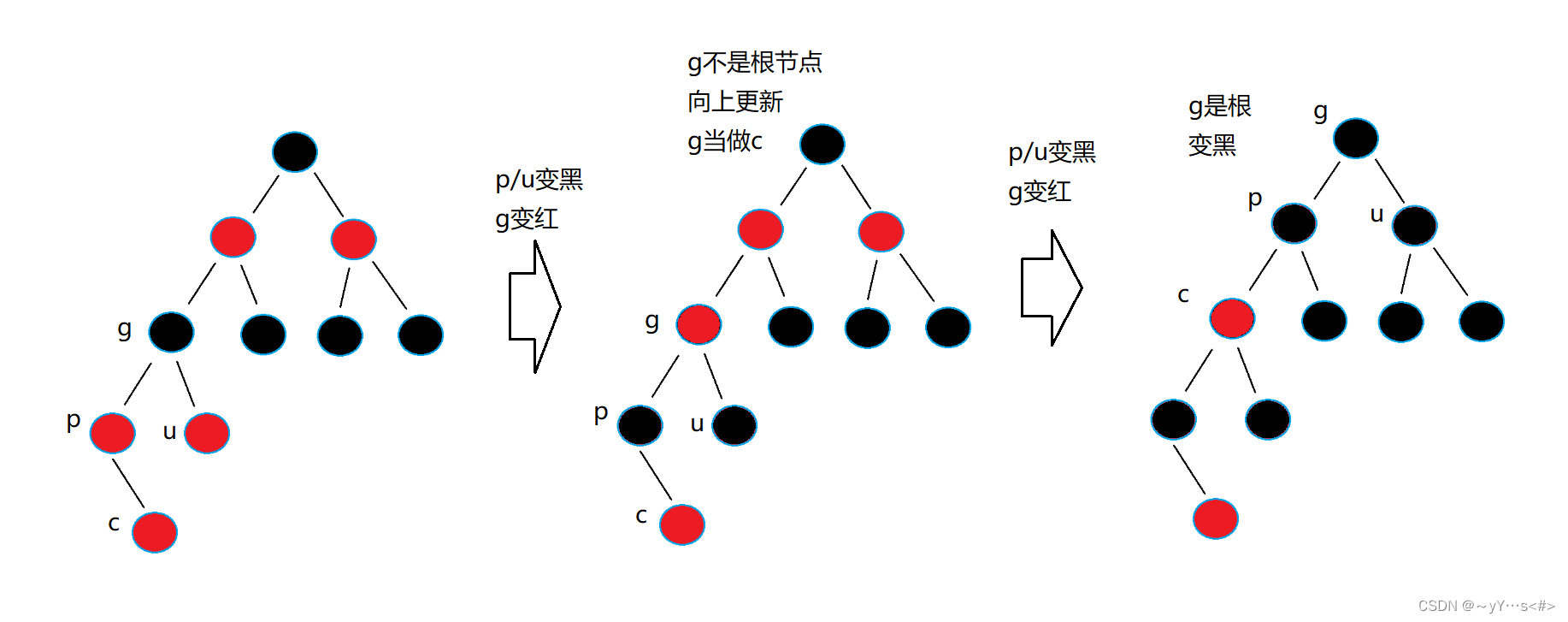
情况二:叔叔不存在或者叔叔存在且为黑
情况二里面又有4种变色方式(其实与其说是变色方式,不如直接说是旋转方式不同然后根据旋转情况来变色)
1️⃣p是g的左孩子,c是p的左孩子
进行右单旋,p变黑,g变红
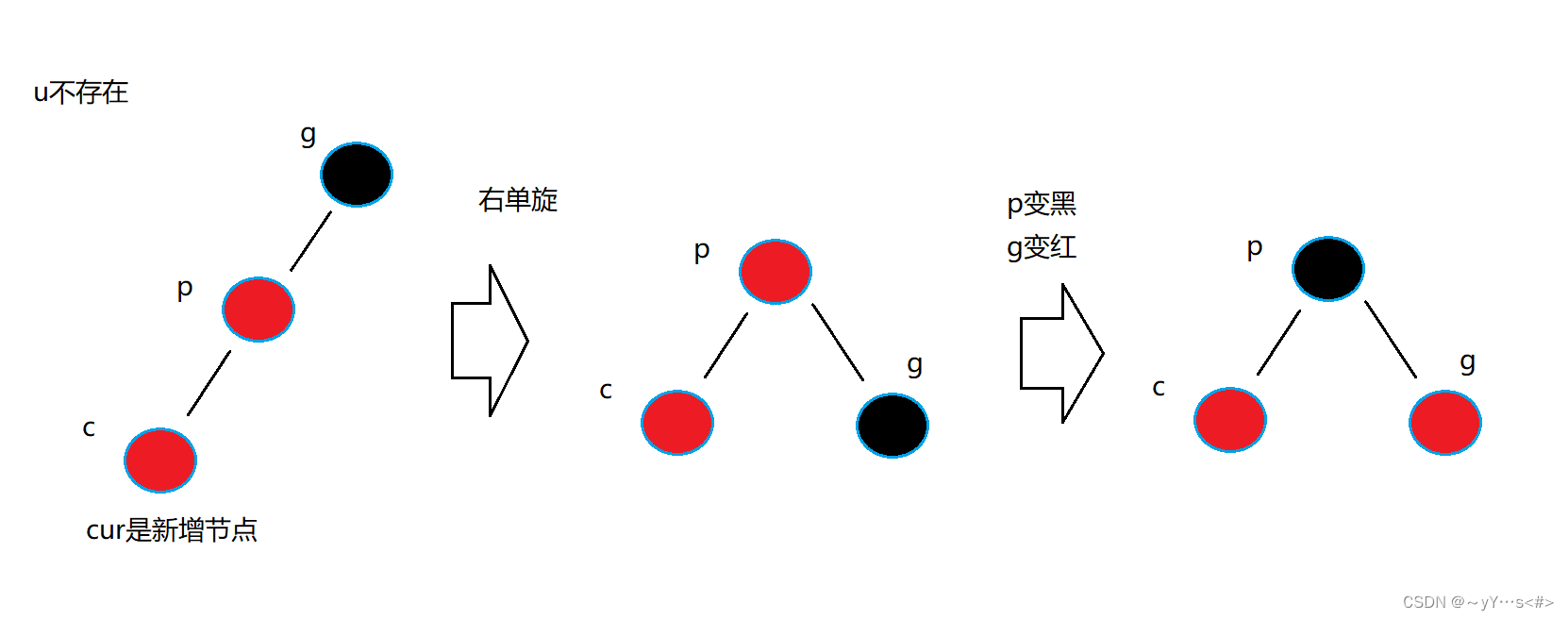
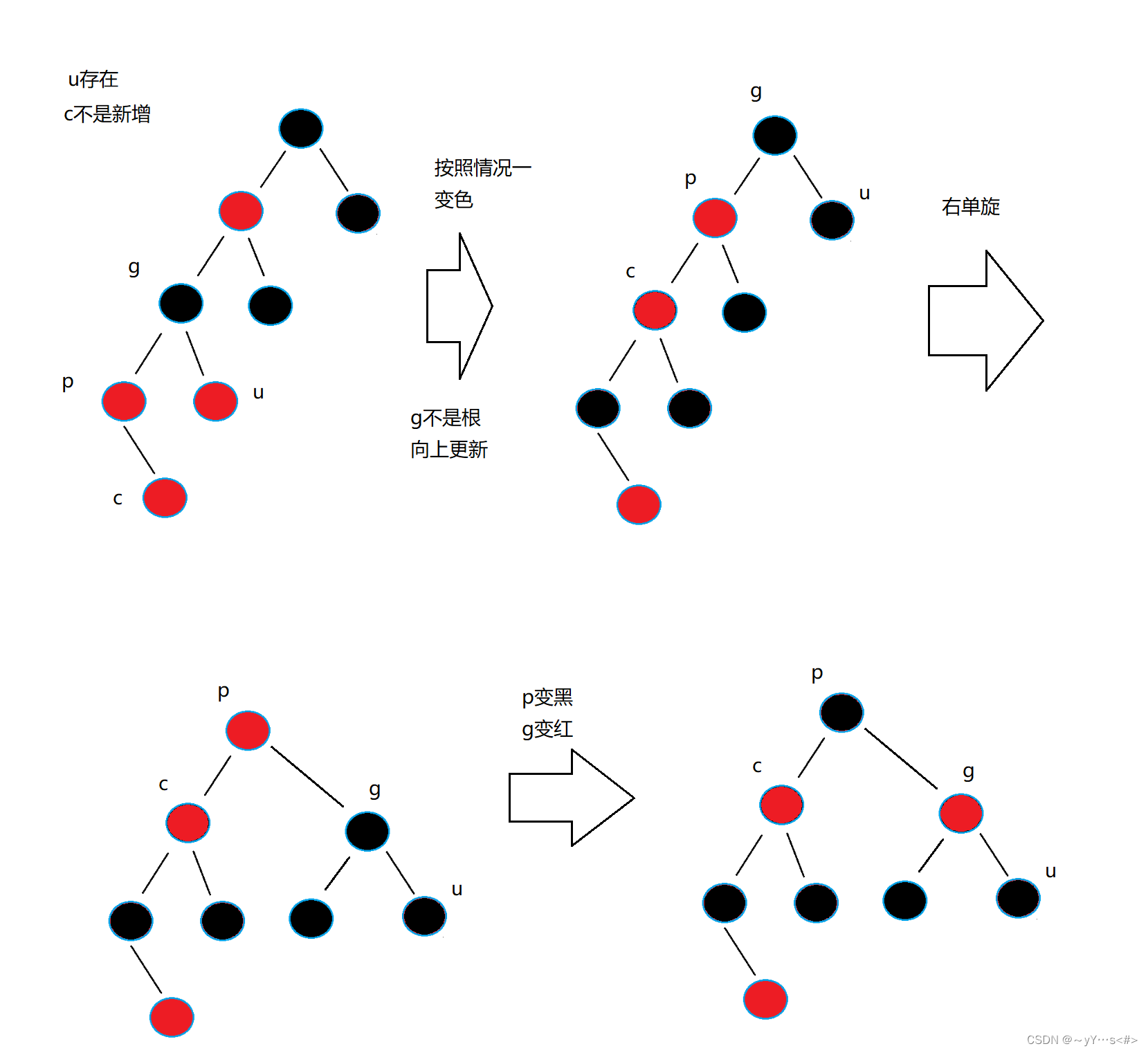
上图的c不是新增,表示的是当它的叔叔节点u存在且为黑时的c不是新增。
注意:
这里u存在或者不存在也有两种情况,第一张图的c是新增的节点,u必然是不存在的,如果存在,会导致每条路径的黑色节点数量不相同;同理,第二张图的c刚开始是黑色的节点,它有自己的子树,是通过后面的向上变色处理才变红的,所以第二张图的u是必须存在的。总之一句话,u存不存在要符合规则
后面就以u不存在的情况处理
2️⃣p是g的右孩子,c是p的右孩子
进行左单旋,p变黑,g变红
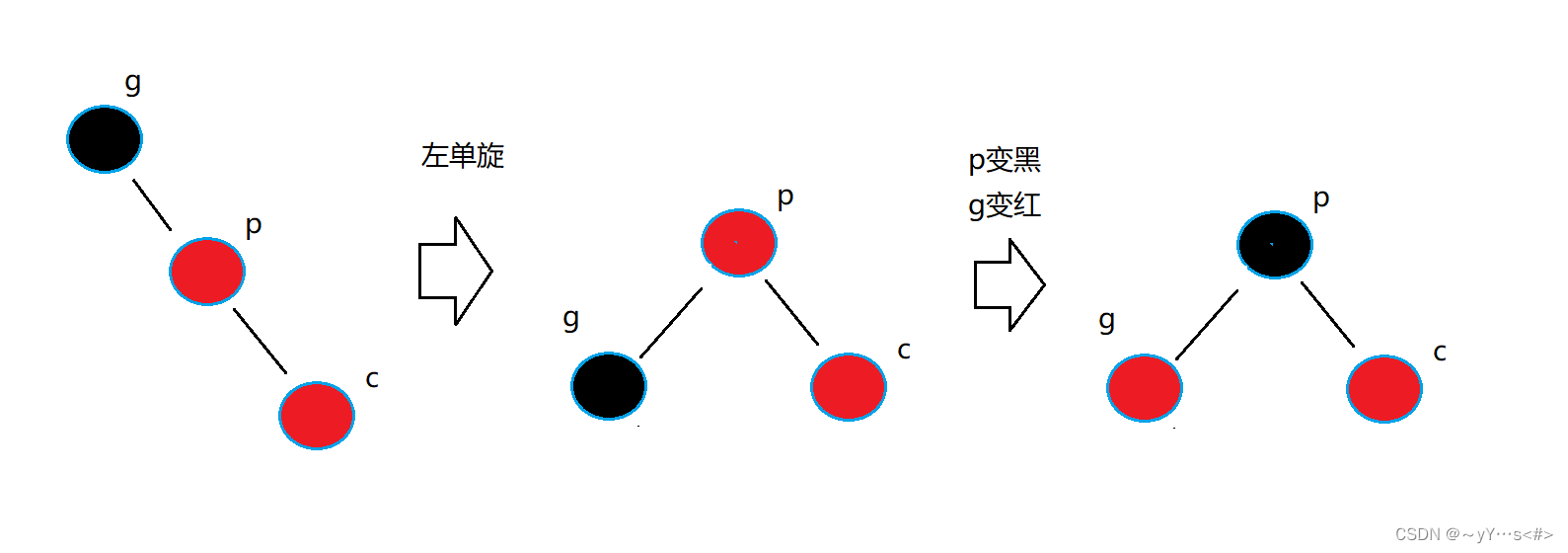
3️⃣p是g的左孩子,c是p的右孩子
先左单旋§,再右单旋(g),g变红,c变黑
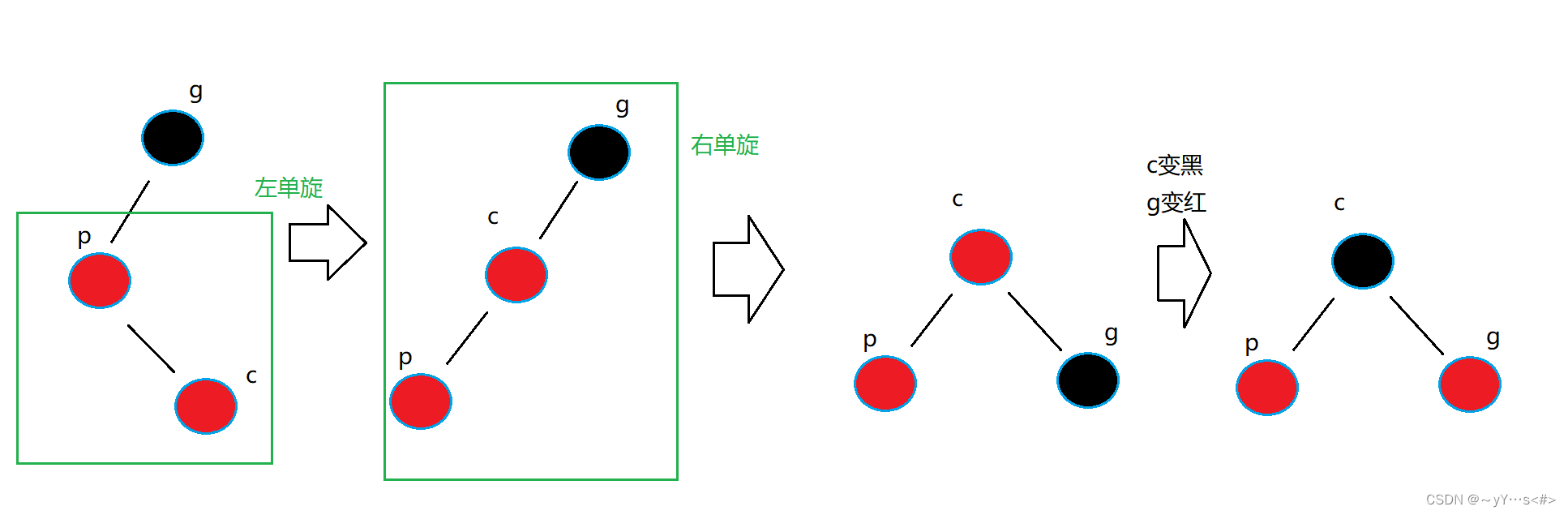
4️⃣p是g的右孩子,c是p的左孩子
先右单旋§,再左单旋(g),g变红,c变黑
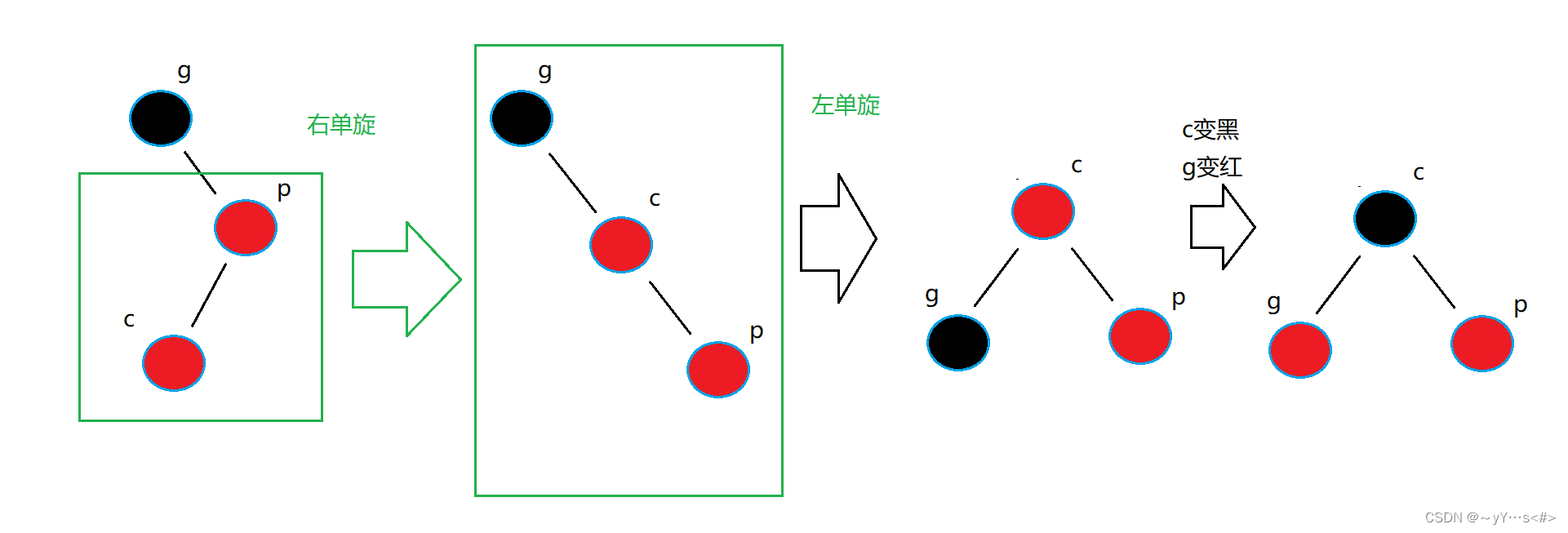
代码:
//插入
bool Insert(const pair<K, V>& kv)
{//为空if (_root == nullptr){_root = new Node(kv);_root->_col = BLACK;//根节点都是黑色的,特殊处理return true;}//非空Node* cur = _root;Node* parent = nullptr;while (cur){if (cur->_kv.first < kv.first){parent = cur;cur = cur->_right;}else if (cur->_kv.first > kv.first){parent = cur;cur = cur->_left;}else{return false;//插入节点不能重复}}//插入新节点cur = new Node(kv);//红色的if (parent->_kv.first < kv.first){parent->_right = cur;}else{parent->_left = cur;}cur->_parent = parent;//调整颜色while (parent && parent->_col == RED){Node* grandfather = parent->_parent;//爷爷节点//父节点在爷爷节点的左边,那么叔叔节点在右边if (parent == grandfather->_left){Node* uncle = grandfather->_right;//情况一:叔叔存在且为红if (uncle && uncle->_col == RED){grandfather->_col = RED;uncle->_col = parent->_col = BLACK;cur = grandfather;//爷爷不是根,向上更新parent = cur->_parent;}//情况二:叔叔不存在/存在且为黑else{//单旋if (cur == parent->_left){RotateR(grandfather);//右单旋parent->_col = BLACK;//变色grandfather->_col = RED;}//左右双旋 // cur == parent->_rightelse{RotateL(parent);//先左单旋RotateR(grandfather);//再右单旋grandfather->_col = RED;//变色cur->_col = BLACK;}}}else//父节点在右边,叔叔在左边{Node* uncle = grandfather->_left;//情况一:叔叔存在且为红if (uncle && uncle->_col == RED){grandfather->_col = RED;uncle->_col = parent->_col = BLACK;cur = grandfather;//爷爷不是根,向上更新parent = cur->_parent;}//情况二:叔叔不存在/存在且为黑else{//单旋if (cur == parent->_right){RotateL(grandfather);//左单旋parent->_col = BLACK;//变色grandfather->_col = RED;}//右左双旋 // cur == parent->_leftelse{RotateR(parent);//先右单旋RotateL(grandfather);//再左单旋grandfather->_col = RED;//变色cur->_col = BLACK;}break;//经过情况二后跳出}}}_root->_col = BLACK;//统一处理,根必须是黑的return true;
}//左单旋
void RotateL(Node* parent)
{RotateSize++;Node* subR = parent->_right;Node* subRL = subR->_left;parent->_right = subRL;//不为空if (subRL){subRL->_parent = parent;}subR->_left = parent;Node* ppnode = parent->_parent;parent->_parent = subR;//处理parent如果为根if (parent == _root){_root = subR;subR->_parent = nullptr;}//不为根,处理与ppnode的连接else{if (ppnode->_left == parent){ppnode->_left = subR;}else{ppnode->_right = subR;}subR->_parent = ppnode;}
}//右单旋
void RotateR(Node* parent)
{RotateSize++;Node* subL = parent->_left;Node* subLR = subL->_right;parent->_left = subLR;//不为空if (subLR){subLR->_parent = parent;}subL->_right = parent;Node* ppnode = parent->_parent;parent->_parent = subL;if (parent == _root){_root = subL;subL->_parent = nullptr;}else{if (ppnode->_left == parent){ppnode->_left = subL;}else{ppnode->_right = subL;}subL->_parent = ppnode;}
}
2.2 与AVL树对比
红黑树与AVL树都是平衡二叉树,那为什么现实中绝大部分是使用红黑树,很少使用AVL树?下面我们来作数据对比,从两者的旋转次数、插入时间、平衡状态和高度来作分析。
测试代码:
RBTree<int, int> t1;
AVLTree<int, int> t2;const int N = 10000000;
vector<int> v;
v.reserve(N);
srand(time(0));for (size_t i = 0; i < N; i++)
{v.push_back(rand() + i);
}size_t begin1 = clock();
for (auto e : v)
{t1.Insert(make_pair(e, e));
}
size_t end1 = clock();size_t begin2 = clock();
for (auto e : v)
{t2.Insert(make_pair(e, e));
}
size_t end2 = clock();
//旋转次数
cout << "RBTree RoateSize:" << t1.getRotateSize() << endl;
cout << "AVLTree RoateSize:" << t2.getRotateSize() << endl;
//插入时间
cout << "RBTree Insert:" << end1 - begin1 << endl;
cout << "AVLTree Insert:" << end2 - begin2 << endl;
//平衡状态
cout << "RBTree IsBalance:" << t1.IsBalance() << endl;
cout << "AVLTree IsBalance:" << t2.IsBalance() << endl;
//树的高度
cout << "RBTree Height:" << t1.Height() << endl;
cout << "AVLTree Height:" << t2.Height() << endl;
//树的节点个数
cout << "RBTree Size:" << t1.Size() << endl;
cout << "AVLTree Size:" << t2.Size() << endl;
插入一千万个数据,运行结果:
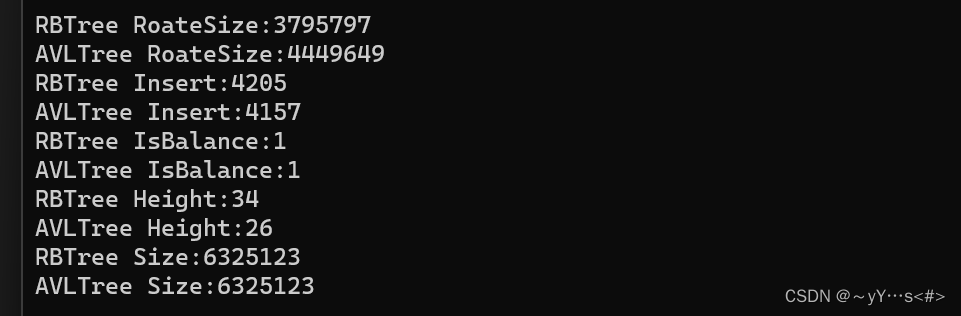
可以发现,红黑树的旋转次数比AVL树少,插入时间相差不大,两种树都是平衡的,红黑树的高度略高一些。
总结:
由于高度上红黑树不会高出多少,所以搜索效率影响不大。从树的高度可知,AVL树是极致追求平衡的,所以要频繁的进行旋转,这也导致旋转次数明显比红黑树多,因此在旋转上开销较大,不及红黑树的性能更优越些,同时红黑树实现比较简单,所以实际运用中红黑树更多。
相关文章:

【C++】实现红黑树
目录 一、认识红黑树1.1 概念1.2 定义 二、实现红黑树2.1 插入2.2 与AVL树对比 一、认识红黑树 1.1 概念 红黑树是一个二叉搜索树,与AVL树相比,红黑树不再使用平衡因子来控制树的左右子树高度差,而是用颜色来控制平衡,颜色为红色…...
)
爬虫(六)
复习回顾: 01.浏览器一个网页的加载全过程1. 服务器端渲染html的内容和数据在服务器进行融合.在浏览器端看到的页面源代码中. 有你需要的数据2. 客户端(浏览器)渲染html的内容和数据进行融合是发生在你的浏览器上的.这个过程一般通过脚本来完成(javascript)我们通过浏览器可以…...

最长连续序列 - LeetCode 热题 3
大家好!我是曾续缘💝 今天是《LeetCode 热题 100》系列 发车第 3 天 哈希第 3 题 ❤️点赞 👍 收藏 ⭐再看,养成习惯 最长连续序列 给定一个未排序的整数数组 nums ,找出数字连续的最长序列(不要求序列元素…...
运营模型—RFM 模型
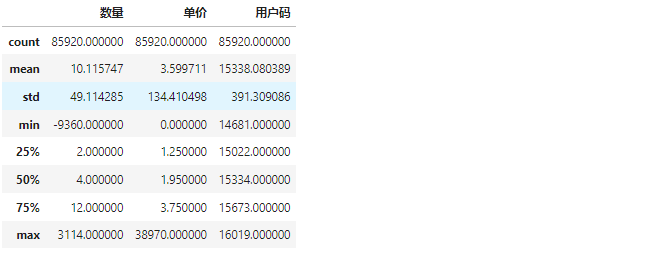
运营模型—RFM 模型 RFM 是什么其实我们前面的文章介绍过,这里我们不再赘述,可以参考运营数据分析模型—用户分层分析,今天我们要做的事情是如何落地RFM 模型 我们的数据如下,现在我们就开始进行数据处理 数据预处理 因为数据预处理没有一个固定的套路,都是根据数据的实…...
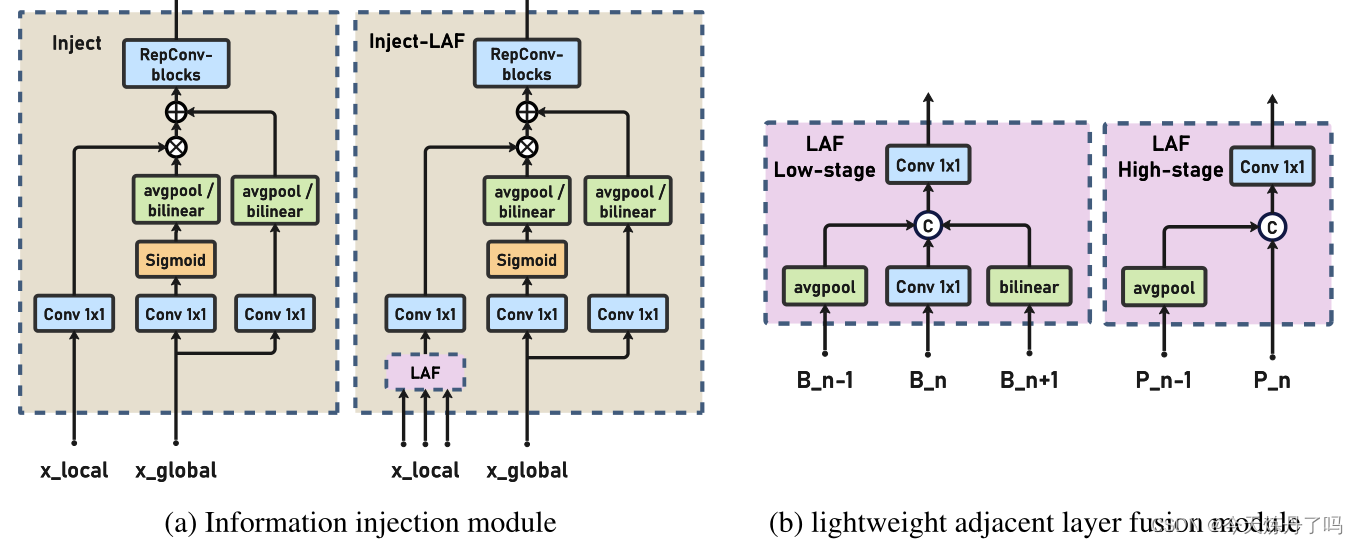
YOLOv9|加入2023Gold YOLO中的GD机制!遥遥领先!
专栏介绍:YOLOv9改进系列 | 包含深度学习最新创新,助力高效涨点!!! 一、Gold YOLO摘要 在过去的几年里,YOLO系列模型已经成为实时目标检测领域的领先方法。许多研究通过修改体系结构、增加数据和设计新的损…...
WRF模型运行教程(ububtu系统)--III.运行WRF模型(官网案例)
零、创建DATA目录 # 1.创建一个DATA目录用于存放数据(一般为fnl数据,放在Build_WRF目录下)。 mkdir DATA # 2.进入 DATA cd DATA 一、WPS预处理 在模拟之前先确定模拟域(即模拟范围),并进行数据预处理(…...
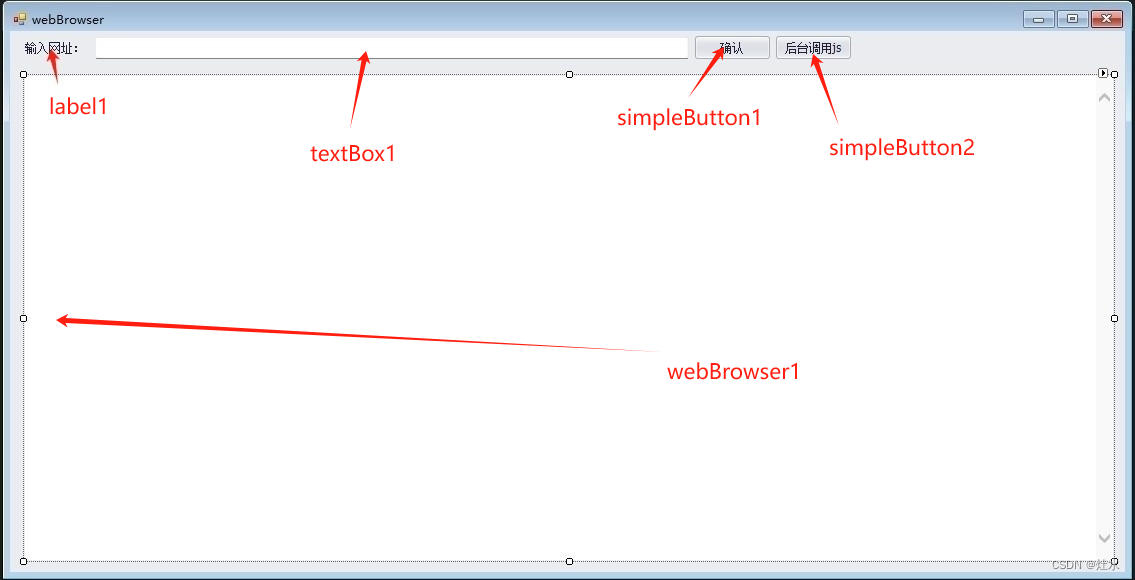
html和winform webBrowser控件交互并播放视频(包含转码)
1、 为了使网页能够与winform交互 将com的可访问性设置为真 [System.Security.Permissions.PermissionSet(System.Security.Permissions.SecurityAction.Demand, Name "FullTrust")][System.Runtime.InteropServices.ComVisibleAttribute(true)] 2、在webBrow…...
Neo4j 批量导入数据 从官方文档学习LOAD CSV 命令 小白可食用版
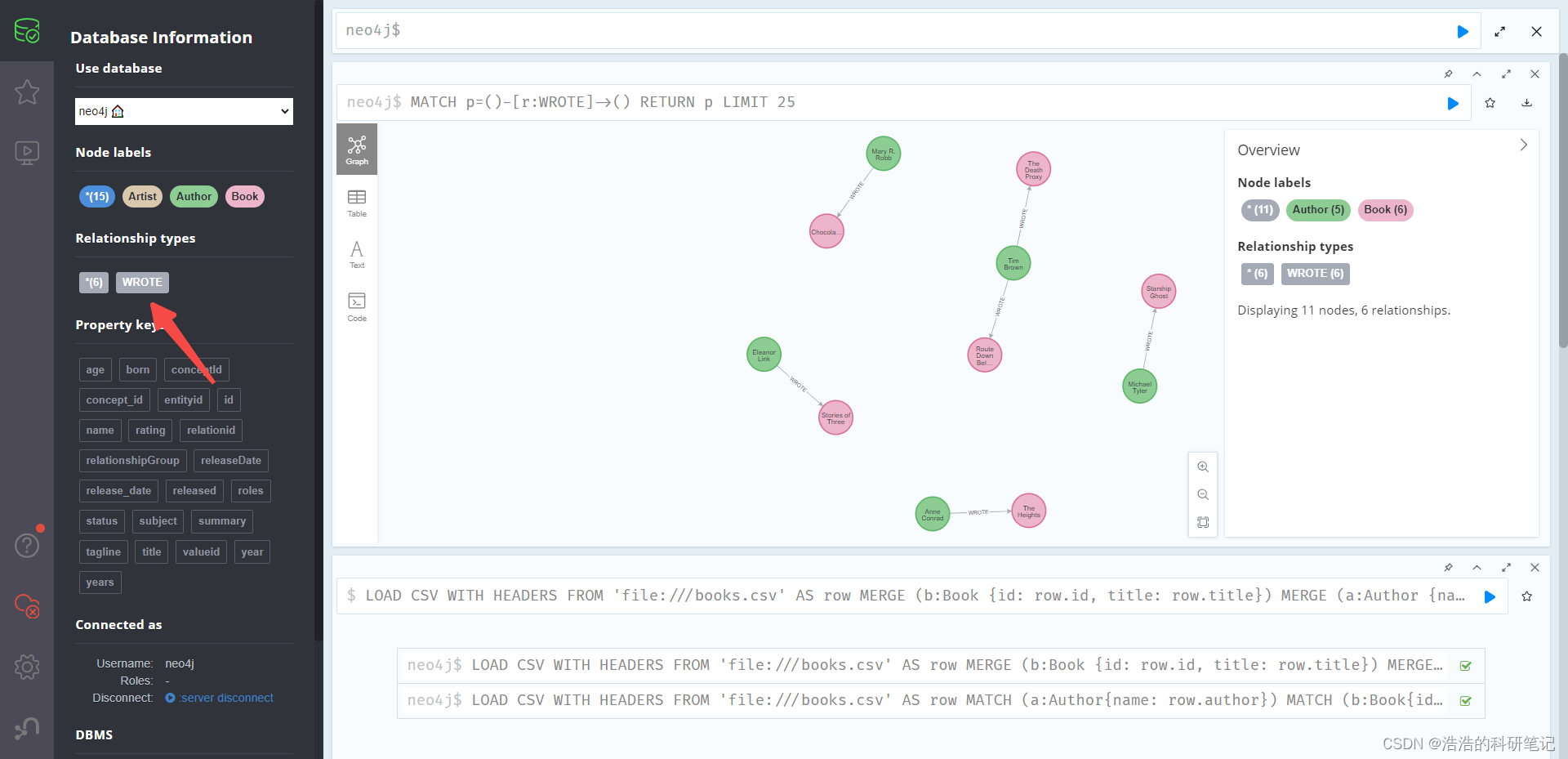
学习LOAD CSV🚀 在使用Neo4j进行大量数据导入的时候,发现如果用代码自动一行一行的导入效率过低,因此明白了为什么需要用到批量导入功能,在Neo4j中允许批量导入CSV文件格式,刚开始从网上的中看了各种半残的博客或者视频…...
Day43-2-企业级实时复制intofy介绍及实践
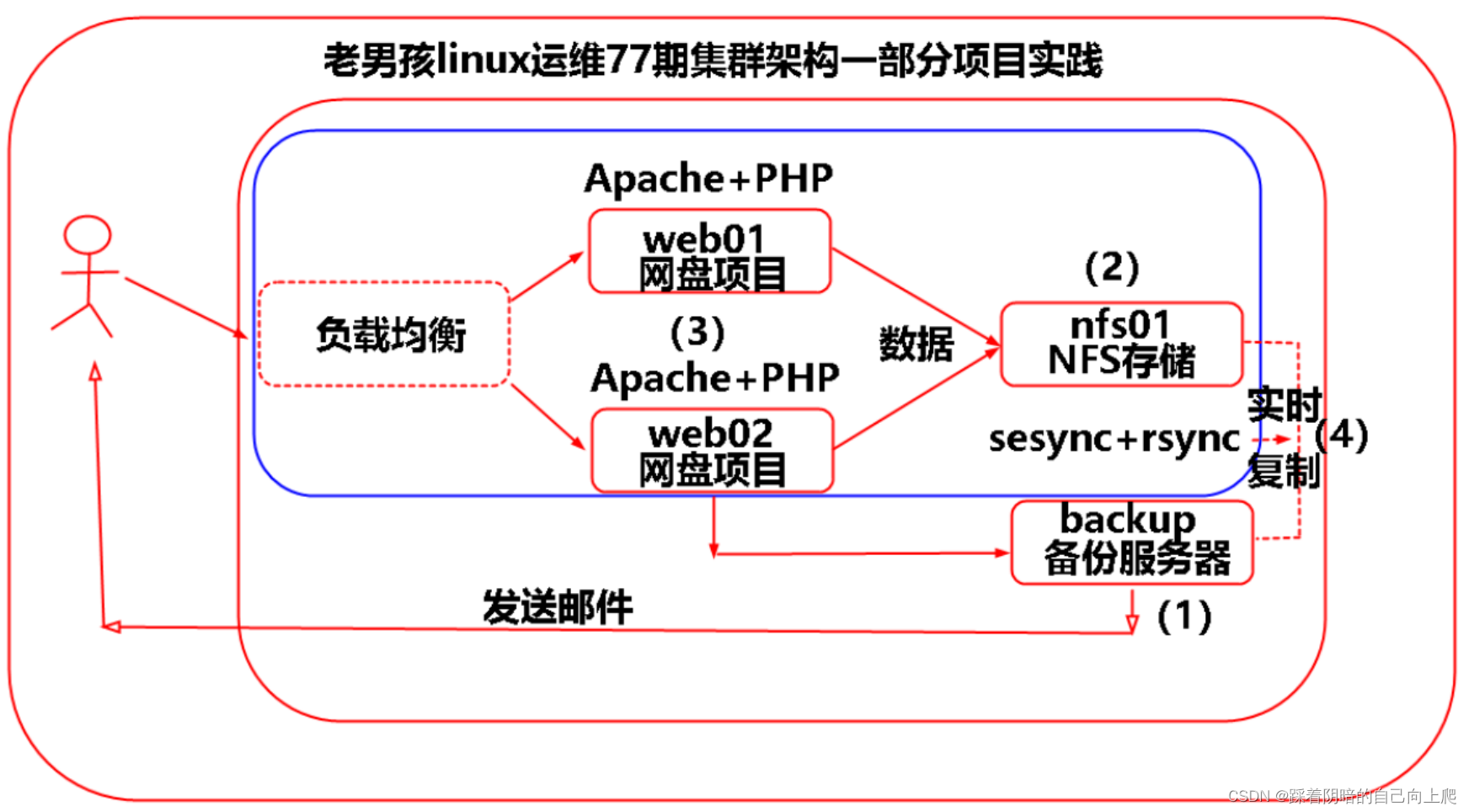
Day43-2-企业级实时复制intofy介绍及实践 1. 企业级备份方案介绍1.1 利用定时方式,实现周期备份重要数据信息。1.2 实时数据备份方案1.3 实时复制环境准备1.4 实时复制软件介绍1.5 实时复制inotify机制介绍1.6 项目部署实施1.6.1 部署环境准备1.6.2 检查Linux系统支…...

2024年AI辅助研发趋势深度解析:科技革新与效率提升的双重奏
随着人工智能技术的迅猛发展,AI辅助研发正逐渐成为科技界和工业界的热门话题。特别是在2024年,这一趋势将更加明显,AI辅助研发将在各个领域展现出强大的潜力和应用价值。 首先,AI辅助研发将进一步提升研发效率。传统的研发模式往…...

bash: mysqldump: command not found
问题:在linux上执行mysql备份的时候,出现此异常 mysqldump命令找不到 解决: 1、找到mysql目录(找到mysql可执行命令目录) which mysql 有图可知,mysql安装在: /usr1/local/java/mysql 2、my…...

hcie数通和云计算选哪个好?
1. 基础知识与技能要求 数通技术是网络技术的核心,它涉及到网络协议、路由交换、网络安全等多个方面。如果你是一名网络工程师或开发者,想要在数通领域有所建树,你需要具备扎实的基础知识和丰富的实战经验。 云计算则更注重于虚拟化、存储、网…...
浅易理解:非极大抑制NMS
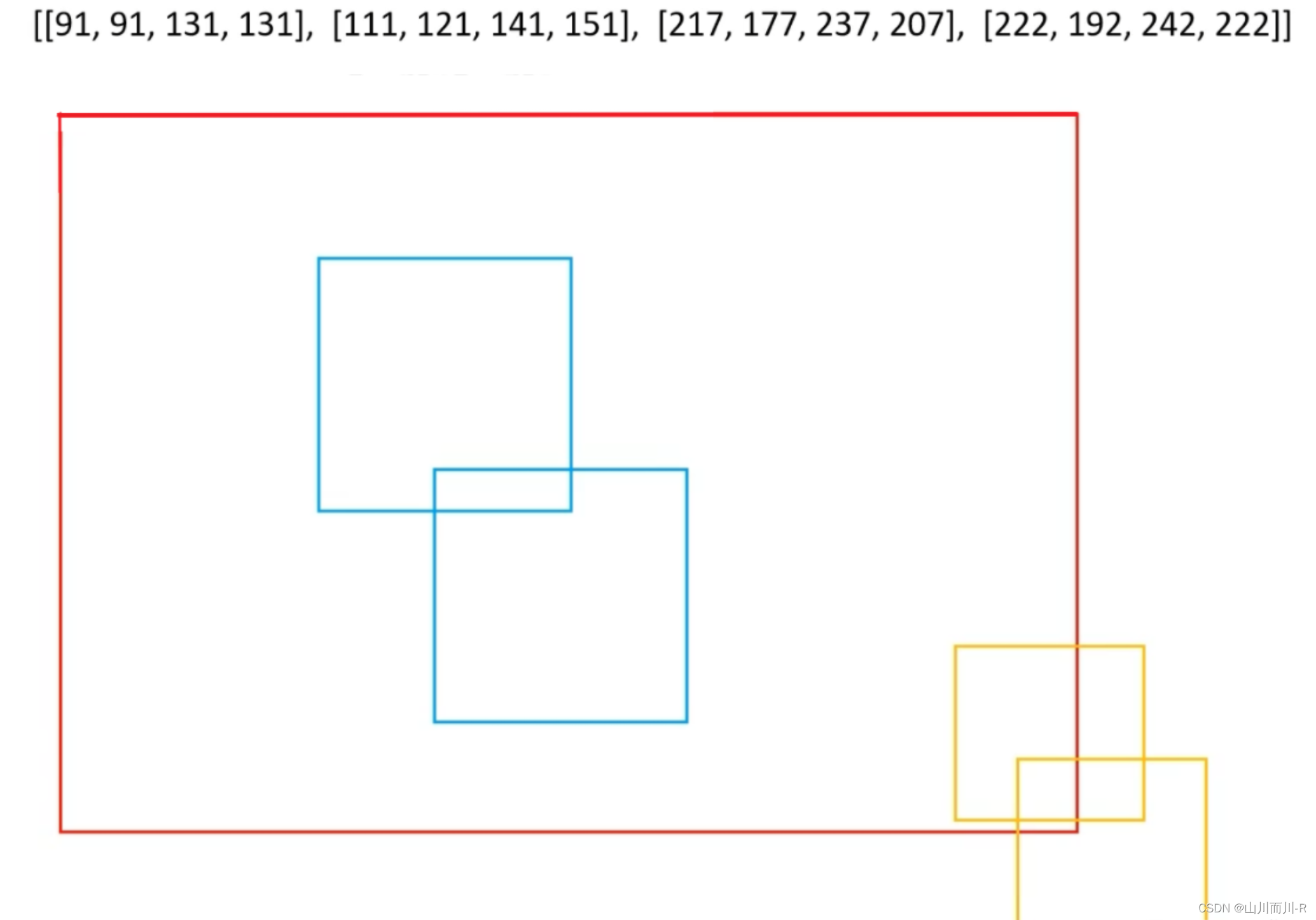
什么是非极大抑制NMS 非极大值抑制(Non-Maximum Suppression,简称NMS)是一种在计算机视觉和图像处理领域中广泛使用的后处理技术,特别是在目标检测任务中。它的主要目的是解决目标检测过程中出现的重复检测问题,即对于…...

C语言如何进⾏字符数组的复制?
一、问题 有两个字符数组a和b,a的值是“Good Bye” ,b的值是 “Bye Bye”,现在要把b 复制到a中,使a变成“Bye Bye”,应该怎么做? 二、解答 在字符串操作中,字符串复制是⽐较常⽤的操作之⼀。在…...

Linux 中搭建 主从dns域名解析服务器
CSDN 成就一亿技术人! 作者主页:点击! Linux专栏:点击! CSDN 成就一亿技术人! ————前言———— 主从(Master-Slave)DNS架构是一种用于提高DNS系统可靠性和性能的配置方式。…...

CSS3病毒病原体图形特效
CSS3病毒病原体图形特效,源码由HTMLCSSJS组成,双击html文件可以本地运行效果,也可以上传到服务器里面 下载地址 CSS3病毒病原体图形特效代码...
Tomcat Web 开发项目构建教程
1下载Tomcat安装包,下载链接:Apache Tomcat - Welcome!,我电脑环境为JDK8,所以下载Tomcat9.0 2、下载完压缩包后,解压到指定位置 3.在intelij中新建一个项目 4.选中创建的项目,双击shift,输入add frame...然…...
 gauss的使用)
Elasticsearch(9) gauss的使用
elasticsearch version: 7.10.1 在Elasticsearch中,gauss作为衰减函数(decay function)被用于function_score查询中,用于实现基于地理位置或其他数值字段的衰减权重评分。gauss衰减函数模拟了高斯分布,即距…...

php前端和java后端数据调用流程
php前端和java后端数据调用流程 前端 1、新建php页面title.php <title>标题</title> <td width"30%" class"form-key">标题内容</td> <td width"70%"><input type"text" class"form-control…...
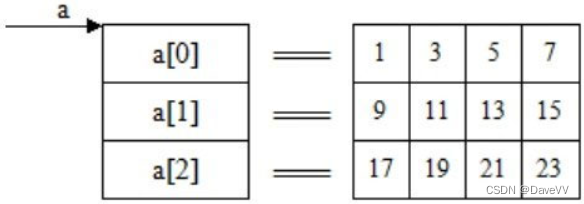
C语言从入门到熟悉------第四阶段
指针 地址和指针的概念 要明白什么是指针,必须先要弄清楚数据在内存中是如何存储的,又是如何被读取的。如果在程序中定义了一个变量,在对程序进行编译时,系统就会为这个变量分配内存单元。编译系统根据程序中定义的变量类型分配…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

51c自动驾驶~合集58
我自己的原文哦~ https://blog.51cto.com/whaosoft/13967107 #CCA-Attention 全局池化局部保留,CCA-Attention为LLM长文本建模带来突破性进展 琶洲实验室、华南理工大学联合推出关键上下文感知注意力机制(CCA-Attention),…...

微软PowerBI考试 PL300-选择 Power BI 模型框架【附练习数据】
微软PowerBI考试 PL300-选择 Power BI 模型框架 20 多年来,Microsoft 持续对企业商业智能 (BI) 进行大量投资。 Azure Analysis Services (AAS) 和 SQL Server Analysis Services (SSAS) 基于无数企业使用的成熟的 BI 数据建模技术。 同样的技术也是 Power BI 数据…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

数据库分批入库
今天在工作中,遇到一个问题,就是分批查询的时候,由于批次过大导致出现了一些问题,一下是问题描述和解决方案: 示例: // 假设已有数据列表 dataList 和 PreparedStatement pstmt int batchSize 1000; // …...

Spring AI与Spring Modulith核心技术解析
Spring AI核心架构解析 Spring AI(https://spring.io/projects/spring-ai)作为Spring生态中的AI集成框架,其核心设计理念是通过模块化架构降低AI应用的开发复杂度。与Python生态中的LangChain/LlamaIndex等工具类似,但特别为多语…...

关键领域软件测试的突围之路:如何破解安全与效率的平衡难题
在数字化浪潮席卷全球的今天,软件系统已成为国家关键领域的核心战斗力。不同于普通商业软件,这些承载着国家安全使命的软件系统面临着前所未有的质量挑战——如何在确保绝对安全的前提下,实现高效测试与快速迭代?这一命题正考验着…...

虚拟电厂发展三大趋势:市场化、技术主导、车网互联
市场化:从政策驱动到多元盈利 政策全面赋能 2025年4月,国家发改委、能源局发布《关于加快推进虚拟电厂发展的指导意见》,首次明确虚拟电厂为“独立市场主体”,提出硬性目标:2027年全国调节能力≥2000万千瓦࿰…...

莫兰迪高级灰总结计划简约商务通用PPT模版
莫兰迪高级灰总结计划简约商务通用PPT模版,莫兰迪调色板清新简约工作汇报PPT模版,莫兰迪时尚风极简设计PPT模版,大学生毕业论文答辩PPT模版,莫兰迪配色总结计划简约商务通用PPT模版,莫兰迪商务汇报PPT模版,…...

08. C#入门系列【类的基本概念】:开启编程世界的奇妙冒险
C#入门系列【类的基本概念】:开启编程世界的奇妙冒险 嘿,各位编程小白探险家!欢迎来到 C# 的奇幻大陆!今天咱们要深入探索这片大陆上至关重要的 “建筑”—— 类!别害怕,跟着我,保准让你轻松搞…...
