【智能算法】秃鹰搜索算法(BES)原理及实现

目录
- 1.背景
- 2.算法原理
- 2.1算法思想
- 2.2算法过程
- 3.结果展示
- 4.参考文献
1.背景
2020年, Alsattar等人受到秃鹰猎食自然行为启发,提出了秃鹰搜索算法(Bald Eagle Search,BES)。
2.算法原理
2.1算法思想
BES主要分为三个阶段选择搜索空间、搜索空间猎物和俯冲捕获猎物。

2.2算法过程
选择搜索空间:
秃鹰个体在飞行中的位置代表 1个可行解,在选择搜索空间阶段,秃鹰会挑选猎物聚集数量最多的区域当做搜索空间,该阶段的秃鹰行为由如下方程描述:
P i , n e w ( t ) = P b e s t ( t ) + α × r × ( P m e a n ( t ) − P i ( t ) ) (1) P_{i,\mathrm{new}}(t)=P_{\mathrm{best}}(t)+\alpha\times r\times(P_{\mathrm{mean}}(t)-P_{i}(t))\tag{1} Pi,new(t)=Pbest(t)+α×r×(Pmean(t)−Pi(t))(1)
其中,Pi,new(t)表示第 i 只秃鹰的更新位置;Pbest(t)表示秃鹰最佳搜索位置;Pmean(t)表示秃鹰之前搜索结束后所有秃鹰个体的平均分布位置,Pi(t)表示第 i只秃鹰的搜索位置,称作领导者;t是当前迭代次数,参数 α∈[1.5,2]是控制秃鹰搜索位置的参数,参数 α 设置为 2;r 是取值范围在 0~1之间的随机数。
搜索空间猎物:
秃鹰个体在完成选择目标搜索空间后,会在该搜索空间中对猎物进行“螺旋式”搜索,并向不同的方向飞行移动以加速搜索进程。该阶段的秃鹰行为如下方程描述:
P i , n e w ( t ) = P i ( t ) + x ( i ) × ( P i ( t ) − P m e a n ( t ) ) + y ( i ) × ( P i ( t ) − P i + 1 ( t ) ) x ( i ) = x r ( i ) max ( ∣ x r ∣ ) , y ( i ) = y r ( i ) max ( ∣ y r ∣ ) x r ( i ) = r ( i ) × sin ( θ ( i ) ) , y r ( i ) = r ( i ) × cos ( θ ( i ) ) θ ( i ) = a × π × r a n d , r ( i ) = θ ( i ) + R × r a n d (2) \begin{aligned} &P_{i,\mathrm{new}}(t)=P_{i}(t)+x(i)\times(P_{i}(t)-P_{\mathrm{mean}}(t))+y(i)\times \left(P_{i}(t)-P_{i+1}(t)\right) \\ &x(i)=\frac{x_{r}(i)}{\operatorname*{max}(\left|x_{r}\right|)},y(i)=\frac{y_{r}(i)}{\operatorname*{max}(\left|y_{r}\right|)} \\ &x_{_r}(i)=r(i)\times\sin(\theta(i)),y_{_r}(i)=r(i)\times\cos(\theta(i)) \\ &\theta(i)=a\times\pi\times\mathrm{rand},r(i)=\theta(i)+R\times\mathrm{rand} \end{aligned} \tag{2} Pi,new(t)=Pi(t)+x(i)×(Pi(t)−Pmean(t))+y(i)×(Pi(t)−Pi+1(t))x(i)=max(∣xr∣)xr(i),y(i)=max(∣yr∣)yr(i)xr(i)=r(i)×sin(θ(i)),yr(i)=r(i)×cos(θ(i))θ(i)=a×π×rand,r(i)=θ(i)+R×rand(2)
其中,x(i)与 y(i)表示极坐标中秃鹰的位置,取值范围均为(-1,1);θ(i)与 r(i)分别表示螺旋方程的极角与极径;a∈[5,10]与 R∈(0.5,2)表示控制秃鹰螺旋飞行轨迹的参数。
俯冲捕获猎物:
秃鹰在搜索空间锁定目标猎物后,从最佳位置快速飞行至目标猎物位置,与此同时所有的秃鹰个体也会朝着最佳位置飞行移动。该阶段的秃鹰行为由如下方程描述:
P i , n e w ( t ) = r a n d × P b e s t ( t ) + x 1 ( i ) × ( P i ( t ) − c 1 × P m e a n ( t ) ) + y 1 ( i ) × ( P i ( t ) − c 2 × P b e s t ( t ) ) x 1 ( i ) = x r ( i ) max ( ∣ x r ∣ ) , y 1 ( i ) = y r ( i ) max ( ∣ y r ∣ ) x r ( i ) = r ( i ) × sinh ( θ ( i ) ) , y r ( i ) = r ( i ) × cosh ( θ ( i ) ) θ ( i ) = a × π × r a n d , r ( i ) = θ ( i ) (3) \begin{aligned} &&&P_{i,new}(t)=\mathrm{rand}\times P_{\mathrm{best}}(t)+x_{1}\left(i\right)\times\left(P_{i}(t)-c_{1}\times P_{\mathrm{mean}}(t)\right)+ y_{1}\left(i\right)\times\left(P_{i}(t)-c_{2}\times P_{\mathrm{best}}(t)\right) &&&& \\ &&&x_{1}\left(i\right)=\frac{x_{r}\left(i\right)}{\operatorname*{max}(\left|x_{r}\right|)},y_{1}\left(i\right)=\frac{y_{r}\left(i\right)}{\operatorname*{max}(\left|y_{r}\right|)}&& \\ &&&x_{r}(i)=r(i)\times\sinh\left(\theta(i)\right),y_{r}(i)=r(i)\times\cosh\left(\theta(i)\right)&& \\ &&&\theta(i)=a\times\pi\times\mathrm{rand},r(i)=\theta(i)&& \end{aligned}\tag{3} Pi,new(t)=rand×Pbest(t)+x1(i)×(Pi(t)−c1×Pmean(t))+y1(i)×(Pi(t)−c2×Pbest(t))x1(i)=max(∣xr∣)xr(i),y1(i)=max(∣yr∣)yr(i)xr(i)=r(i)×sinh(θ(i)),yr(i)=r(i)×cosh(θ(i))θ(i)=a×π×rand,r(i)=θ(i)(3)
伪代码:

3.结果展示
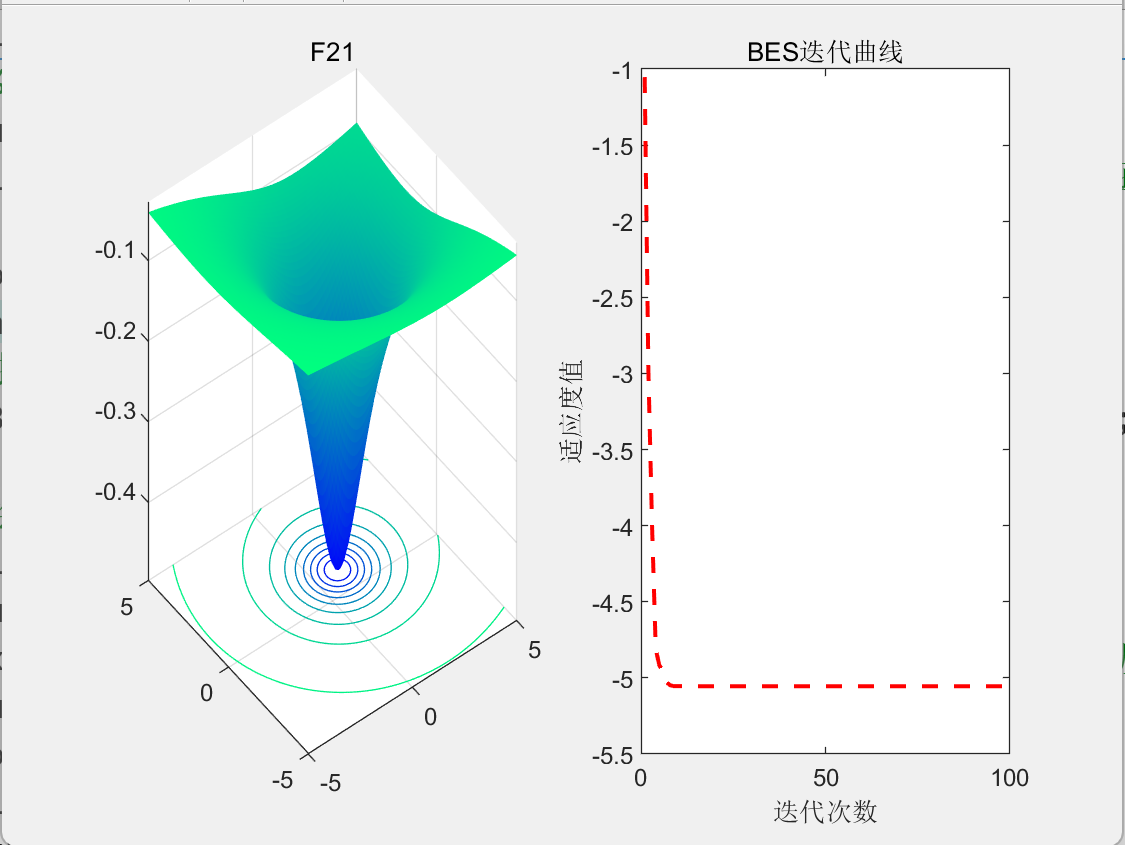
4.参考文献
[1] Alsattar H A, Zaidan A A, Zaidan B B. Novel meta-heuristic bald eagle search optimisation algorithm[J]. Artificial Intelligence Review, 2020, 53: 2237-2264.
相关文章:

【智能算法】秃鹰搜索算法(BES)原理及实现
目录 1.背景2.算法原理2.1算法思想2.2算法过程 3.结果展示4.参考文献 1.背景 2020年, Alsattar等人受到秃鹰猎食自然行为启发,提出了秃鹰搜索算法(Bald Eagle Search,BES)。 2.算法原理 2.1算法思想 BES主要分为三…...

前端并发控制
本文讲解Promise,callback,RxJS多种方式实现并发限制 1.Promise 目前来说,Promise是最通用的方案,一般我们最先想到Promise.all,当然最好是使用新出的Promise.allsettled。 下面简单介绍下二者的区别,假…...

基于YOLOv8深度学习的橙子病害智能诊断与防治系统【python源码+Pyqt5界面+数据集+训练代码】深度学习实战、目标分类
《博主简介》 小伙伴们好,我是阿旭。专注于人工智能、AIGC、python、计算机视觉相关分享研究。 ✌更多学习资源,可关注公-仲-hao:【阿旭算法与机器学习】,共同学习交流~ 👍感谢小伙伴们点赞、关注! 《------往期经典推…...

Java中的多线程详解(超级简单理解)(上篇)
使用工具 IntelliJ IDEA Community Edition 2023.1.4 使用语言 Java8 代码能力快速提升小方法,看完代码自己敲一遍,十分有用 目录 1.多线程概述 1.1 进程与线程 1.2 多线程的运行机制 1.3 多线程的优势 2.多线程编程 2.1 Thread类介绍 2.2 …...

Elastic-Job 分布式任务调度
一、使用场景 (1)分布式项目中 定时任务。如果只部署一台机器,可用性无法保证,如果定时任务机器宕机,无法故障转移,如果部署多台机器时,同一个任务会执行多次,任务重复执行也会出问…...

YZ系列工具之YZ09: VBA_Excel之读心术
我给VBA下的定义:VBA是个人小型自动化处理的有效工具。利用好了,可以大大提高自己的工作效率,而且可以提高数据的准确度。我的教程一共九套一部VBA手册,教程分为初级、中级、高级三大部分。是对VBA的系统讲解,从简单的…...

Python下载音乐
今天我就来分享一下我的方法:Python爬虫 在CS dn社区中我浏览了许多关于爬虫代码,可都有各自的缺陷,有的需要ID比较麻烦,这里我编写了一个程序,他只需要输入歌曲名字即可进行搜索爬取并下载 话不多说,下面的程序复制…...

PCL ICP配准高阶用法——统计每次迭代的配准误差并可视化
目录 一、概述二、代码实现三、可视化代码四、结果展示本文由CSDN点云侠原创,原文链接。如果你不是在点云侠的博客中看到该文章,那么此处便是不要脸的爬虫。 一、概述 在进行论文写作时,需要做对比实验,来分析改进算法的性能,期间用到了迭代误差分布统计的比较分析,为直…...
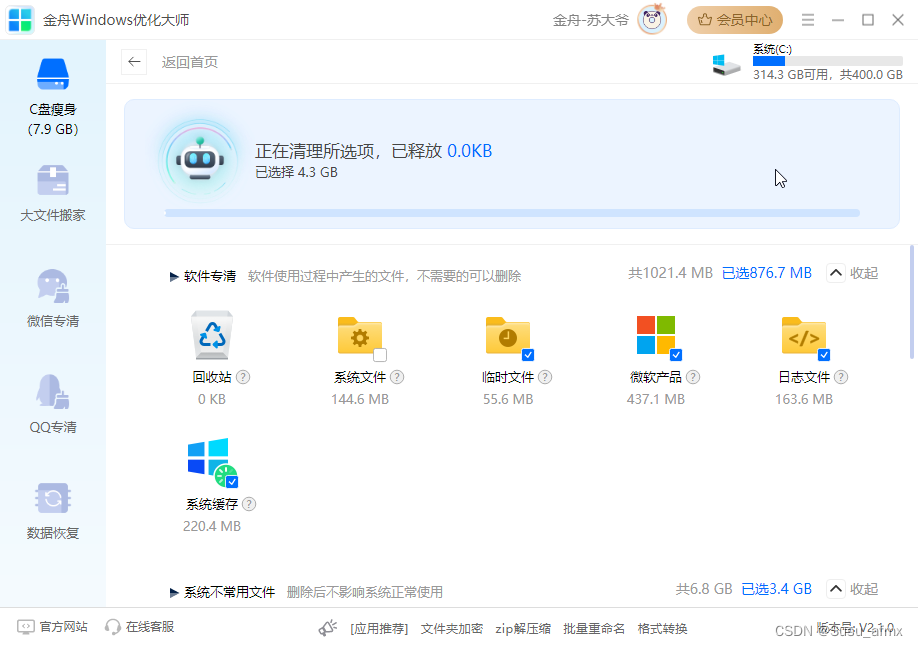
电脑卸载软件怎么清理干净?电脑清理的5种方法
随着我们在电脑上安装和卸载各种软件,很多时候我们会发现,即使软件被卸载,其残留的文件和注册表项仍然存在于电脑中,这不仅占用了宝贵的磁盘空间,还可能影响电脑的性能。那么,如何确保在卸载软件时能够彻底…...

LLM流式方案解决方案和客户端解决方案
背景 接上一篇《LLM大模型统一封装接口解决方案》架构确定后,流式方案非常规请求,需要特殊处理。 本解决方案就是针对上一篇中所需要的流式(打字机效果进行编码) 什么是SSE SSE(Server-Sent Events,服务器发…...

ROS2 高效学习系列
ROS2 高效学习系列 1 说明2 正文 1 说明 2023 年,我们总结输出了 ROS高效入门系列 和 ROS高效进阶系列,系统学习了 ros1 基础知识和 ros 的机器人算法。由于 ros2 的普及,我们将系统学习 ros2 ,包括 ros2 基础知识和相关高级组件…...
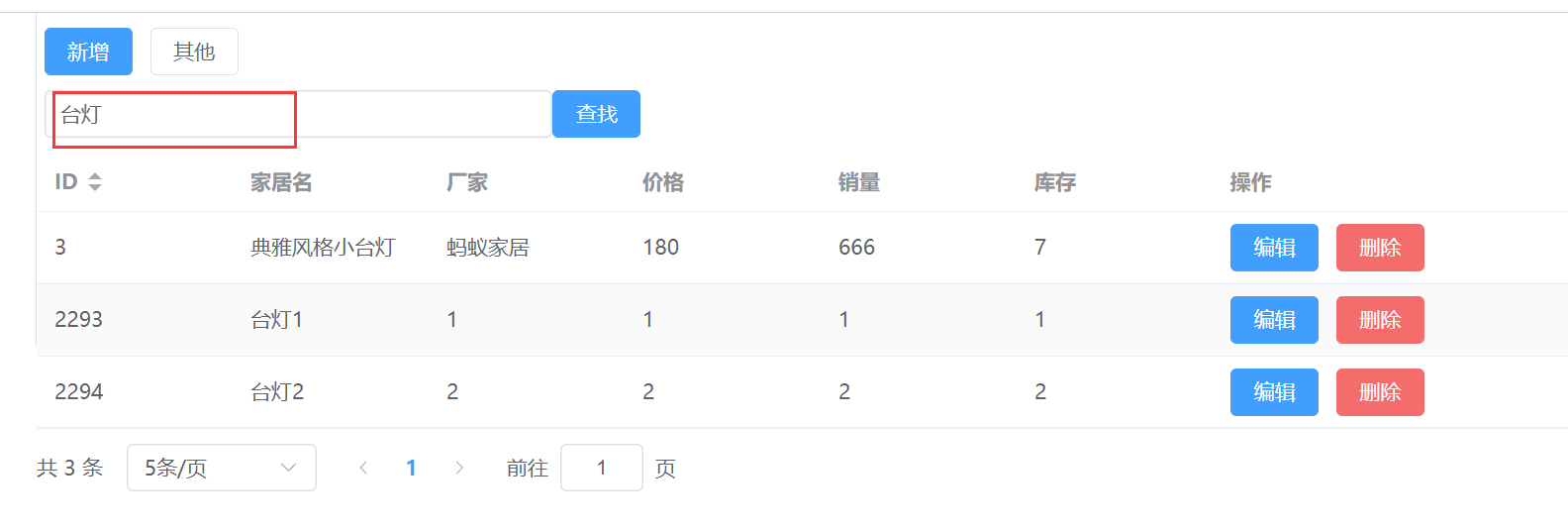
SpringBoot + MyBatisPlus分页查询
文章目录 1.思路分析2.分页查询后端实现1.com/sun/furn/config/MybatisConfig.java 注入MyBatisPlus分页拦截器2.com/sun/furn/controller/FurnController.java 添加方法3.postman测试 3.分页查询前端实现1.src/views/HomeView.vue 引入分页导航条组件2.src/views/HomeView.vue…...

记使用sjson的一次小事故
1. 前言 之前在设计一个兼容函数的时候,使用了sjson动态设入参数,从而实现一些参数的兼容。大致的逻辑如下所示: // 有一堆不规则的json数据 {"a":"aaa","b":"bbb","any_key1":{"k…...
如何在iOS系统抓取log
前言:因为作者目前工作领域和苹果智能家居有关,然后发现一些bug其实是apple sdk原生code的问题,所以需要给apple提radar单,就需要抓ios端Log充当证据给apple看,其实ios抓log非常简单,大家感兴趣可以学习下哦…...
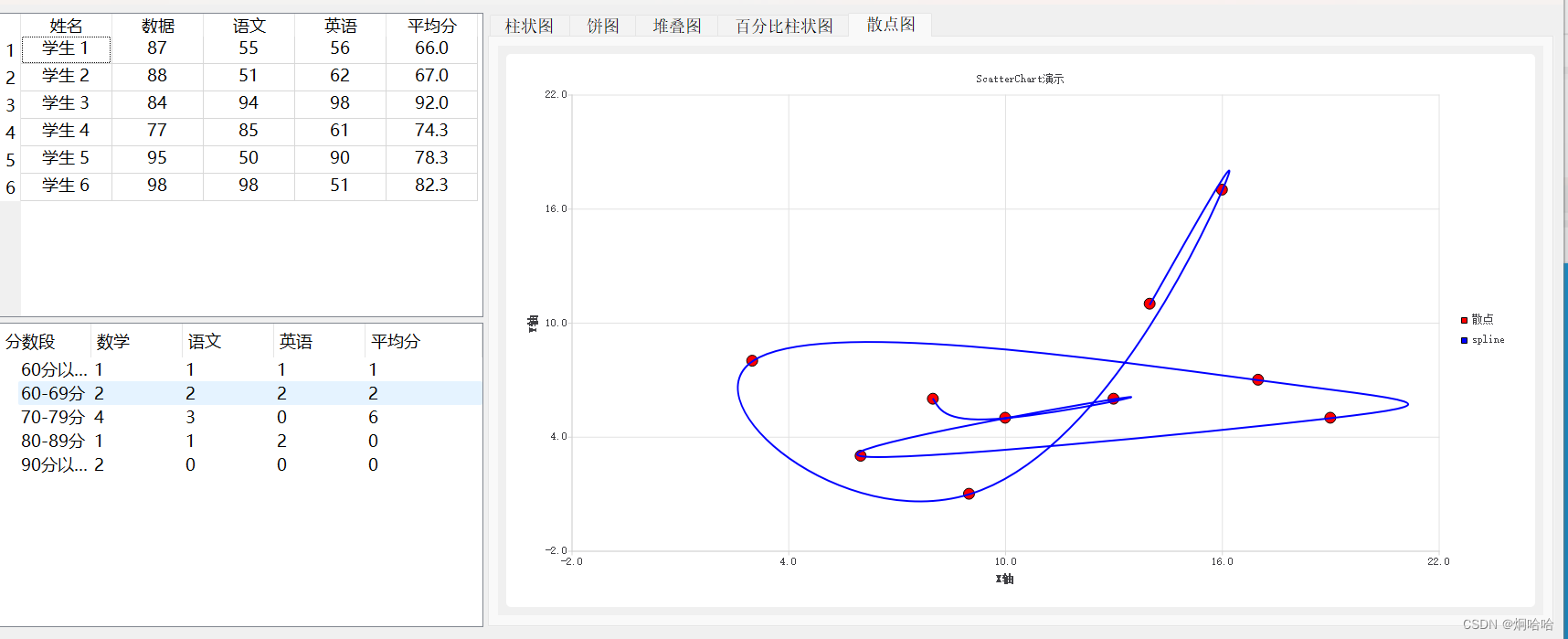
【嵌入式——QT】Charts常见的图表的绘制
【嵌入式——QT】Charts常见的图表的绘制 柱状图QBarSetQBarSeriesQBarCategoryAxis图示 饼图堆叠柱状图百分比柱状图散点图和光滑曲线图代码示例 柱状图 QBarSet 用于创建柱状图的数据集。 主要函数 setLabel():设置数据集标签 ;setLabelBrush()&am…...
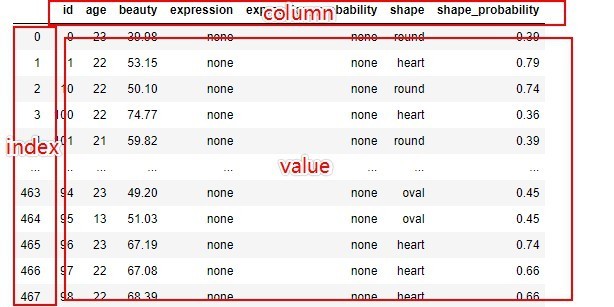
pandas读写excel,csv
1.读excel 1.to_dict() 函数基本语法 DataFrame.to_dict (self, orientdict , into ) --- 官方文档 函数种只需要填写一个参数:orient 即可 ,但对于写入orient的不同,字典的构造方式也不同,官网一共给出了6种,…...
清华大学突破性研究:GVGEN技术,7秒内从文字到3D高保真生成
引言:3D模型生成的挑战与机遇 随着计算机图形学的发展,3D模型的生成在各个行业中变得越来越重要,包括视频游戏设计、电影制作以及AR/VR技术等。在3D建模的不同方面中,从文本描述生成3D模型成为一个特别有趣的研究领域,…...

软件测试要学习的基础知识——黑盒测试
概述 黑盒测试也叫功能测试,通过测试来检测每个功能是否都能正常使用。在测试中,把程序看作是一个不能打开的黑盒子,在完全不考虑程序内部结构和内部特性的情况下,对程序接口进行测试,只检查程序功能是否按照需求规格…...

如何用Airtest脚本连接无线Android设备?
之前我们已经详细介绍过如何用AirtestIDE无线连接Android设备,它的关键点在于,需要先 adb connect 一次,才能点击 connect 按钮无线连接上该设备: 但是有很多同学,在使用纯Airtest脚本的形式连接无线设备时,…...
)
c语言函数大全(C开头)
c语言函数大全(C开头) There is no nutrition in the blog content. After reading it, you will not only suffer from malnutrition, but also impotence. The blog content is all parallel goods. Those who are worried about being cheated should leave quickly. 函数名…...

Linux 文件类型,目录与路径,文件与目录管理
文件类型 后面的字符表示文件类型标志 普通文件:-(纯文本文件,二进制文件,数据格式文件) 如文本文件、图片、程序文件等。 目录文件:d(directory) 用来存放其他文件或子目录。 设备…...

CVPR 2025 MIMO: 支持视觉指代和像素grounding 的医学视觉语言模型
CVPR 2025 | MIMO:支持视觉指代和像素对齐的医学视觉语言模型 论文信息 标题:MIMO: A medical vision language model with visual referring multimodal input and pixel grounding multimodal output作者:Yanyuan Chen, Dexuan Xu, Yu Hu…...
)
【位运算】消失的两个数字(hard)
消失的两个数字(hard) 题⽬描述:解法(位运算):Java 算法代码:更简便代码 题⽬链接:⾯试题 17.19. 消失的两个数字 题⽬描述: 给定⼀个数组,包含从 1 到 N 所有…...

Cloudflare 从 Nginx 到 Pingora:性能、效率与安全的全面升级
在互联网的快速发展中,高性能、高效率和高安全性的网络服务成为了各大互联网基础设施提供商的核心追求。Cloudflare 作为全球领先的互联网安全和基础设施公司,近期做出了一个重大技术决策:弃用长期使用的 Nginx,转而采用其内部开发…...

相机从app启动流程
一、流程框架图 二、具体流程分析 1、得到cameralist和对应的静态信息 目录如下: 重点代码分析: 启动相机前,先要通过getCameraIdList获取camera的个数以及id,然后可以通过getCameraCharacteristics获取对应id camera的capabilities(静态信息)进行一些openCamera前的…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

pikachu靶场通关笔记19 SQL注入02-字符型注入(GET)
目录 一、SQL注入 二、字符型SQL注入 三、字符型注入与数字型注入 四、源码分析 五、渗透实战 1、渗透准备 2、SQL注入探测 (1)输入单引号 (2)万能注入语句 3、获取回显列orderby 4、获取数据库名database 5、获取表名…...

十九、【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建
【用户管理与权限 - 篇一】后端基础:用户列表与角色模型的初步构建 前言准备工作第一部分:回顾 Django 内置的 `User` 模型第二部分:设计并创建 `Role` 和 `UserProfile` 模型第三部分:创建 Serializers第四部分:创建 ViewSets第五部分:注册 API 路由第六部分:后端初步测…...

ubuntu22.04有线网络无法连接,图标也没了
今天突然无法有线网络无法连接任何设备,并且图标都没了 错误案例 往上一顿搜索,试了很多博客都不行,比如 Ubuntu22.04右上角网络图标消失 最后解决的办法 下载网卡驱动,重新安装 操作步骤 查看自己网卡的型号 lspci | gre…...
