2016年认证杯SPSSPRO杯数学建模D题(第二阶段)NBA是否有必要设立四分线全过程文档及程序
2016年认证杯SPSSPRO杯数学建模
D题 NBA是否有必要设立四分线
原题再现:
NBA 联盟从 1946 年成立到今天,一路上经历过无数次规则上的变迁。有顺应民意、皆大欢喜的,比如 1973 年在技术统计中增加了抢断和盖帽数据;有应运而生、力挽狂澜的,比如 1954 年引入 24 秒进攻时限;有因人废事、“打击迫害”的,比如为了限制麦肯,将三秒区宽度从 6 英尺扩大到 12 英尺,又为了限制张伯伦,进一步扩大到 16 英尺;有步步为营、小心翼翼的,比如 2004年在 NBDL 试行所有投篮只算两分,直至第四节最后 5 分钟和加时赛才启用三分球规则;也有弄巧成拙、朝令夕改的,比如 1953 年曾规定每队每名球员单节只能犯规两次,第三次犯规就被罚出场,实施不久之后就不了了之……本质上,NBA 是一个以盈利为目的的商业联赛,为了最大限度地提升比赛观赏性,保证球迷们心甘情愿地掏钱买票,修改现有规则或设立新的规则都是可能的。
79-80 赛季,NBA 开始实验性的引入三分球制,当时的原则是“仅限于常规赛使用”。而在 80-81 赛季,NBA 正式全面引入三分线。目前,NBA 三分线的最远处距离篮筐是 7.25 米。值得注意的是 NBA 曾在 94-95 赛季将三分线距离缩短为 6.70 米,距离变短后人人都能投三分,很难反映出球员的远投能力,所以 97-98 赛季,NBA 又将三分线距离改回原来的 7.25 米。
四分线的推出能更全面反映出 1 名射手的远投能力。2015-2016 赛季,在28-32 英尺(8.53-9.75 米)之间,投篮最准的是快船队的贾马尔·克劳福德,总共 23 次出手命中 14 球,命中率高达 60.9%。排在第 2 位的是湖人队的肯道尔·马绍尔,23 投 11 中,命中率为 47.8%。勇士队的斯蒂芬·库里则以 38.1%(21 投 8 中)的命中率位列第 3 位。NBA 一旦引入四分球制度,投手的春天将就此到来。那些震撼联盟的神射手们又多了一项致命的武器。此外,四分球拉开空间之后,会让内线球员的防守压力变得更小,篮下的肉搏变得更少,更有利于内线的大个子们保持自己的健康。
第二阶段问题:
3. 假设 NBA 联盟决定按照你们的第一阶段的方案设定四分线。这条新规则是否会对三分线的规则产生影响,三分线还是必要的吗?
4. 四分规则一旦出现,可能会改变很多人对于篮球的认识,这有可能是效率最高的一种得分方式。这会对篮球的战术产生什么影响?请举例说明。
整体求解过程概述(摘要)
本文针对NBA联盟建立四分线是否会对三分线规则产生影响和是否有必要保留三分线以及会对篮球战术产生什么影响等问题,以观赏性最大化为目标,运用多种求解方法,对问题建立量化分析、数据分析、物理、逻辑分析、平面动画和类比推理等模型进行求解。
针对问题三,对于四分线规则是否会对三分线规则产生影响,建立量化分析模型和物理模型,进行量化指标得分情况,通过对比得出四分线可能会对三分线产生一定的影响,并建立数学模型来证明是否有保留三分线的必要。
针对问题四,对于四分线会对篮球的战术产生什么影响,首先用层次分析法求出得分方式的权系数,利用权系数建立模糊综合评价对引入四分线的得分方式对战术的影响程度进行粗略计算及评判。再用数据分析法,详细分析三分球进攻(战术)特征及影响因素,然后从三分线规则启用时对原战术的影响,类比推理出四分线对篮球战术所产生的影响,建立平面动画模型,以湖人队为实例,分析三分线对三角战术特征的影响,类比推理出四分线对三角战术特征的影响。用数据分析法对三分线进攻的投篮方式、球员位置、区域、进攻方式、战术配合形式和时间选择的特征进行详细的分析,进而类比推出新的得分方式对战术的影响。
本文通过数据分析得出的三分线进攻特征分析,数据可靠,且参考因素较为详细,误差控制在范围内。最后对我们所建立的一系列模型进行了可行性和可推广性进行了评价和推广。
问题分析:
问题 3 主要是在第一阶段的讨论下,分析四分线规则对三分线规则的影响及三分线是否有存在的必要,通过第一阶段对四分线方案的讨论,我们知道可以从观赏性、逆转的可能性等角度讨论分析。首先,我们把观赏性和逆转的期望进行量化,比较在四分线设定后三分线的数据与以前三分线的数据有无变化,然后通过对比分析四分线设定前后三分规则使用率的变化,另外特别讨论分析了超级远投手库里在四分线规则设定前后三分线的出手的得分率,也可以判断出四分规则对三分线规则有无影响。其次通过对比分析同时存在三分线和四分线的情况与只存在四分线情况的观赏性和逆转的期望来判断三分线是否有保留的必要。
问题 4 主要是分析四分线规则对篮球战术的影响,大范围上讲篮球战术可分为进攻战术、防守战术和争球战术。因为四分球在比赛中的使用有一定的局限性(例如,投手不可能整场比赛一直使用或一整场比赛中不是所有篮球队员都能使用等),所以四分规则对进攻战术、防守战术和争球战术的影响程度有所不同。首先,我们通过比较三分规则对篮球战术的影响,经过类比推理得出四分规则对篮球战术可能产生的影响。其次通过实例战术—三角进攻战术(双掩护+突破或投篮+低位单打)细化到对公牛队在 96—97 赛季和湖人队在 01—02 赛季的数据分析,进而举例说明四分规则对篮球战术的影响。
模型假设:
(1)假设第一阶段结果可靠,可进一步分析。
(2)假设投手的体能投三分和四分基本无变化。
(3)假设比赛中每个队至少名远距离投球队员。
论文缩略图:


全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可
部分程序代码:(代码和文档not free)
A=[1 3 7 8;1/3 1 5 5;1/7 1/5 1 3;1/8 1/5 1/3 1];
[v,d]=eig(A);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil1=(lamda-4)/3;
cr1=cil1/0.90;
b1w=v(:,1)/sum(v(:,1))
B1=[1 2 3;1/2 1 2;1/3 1/2 1];
[v,d]=eig(B1);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil2=(lamda-3)/2;
cr2=cil2/0.58;
b2w=v(:,1)/sum(v(:,1))
B2=[1 1/5 1/2;5 1 7;2 1/7 1];
[v,d]=eig(B2);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil3=(lamda-3)/2;
cr3=cil3/0.58;
b3w=v(:,1)/sum(v(:,1))
B3=[1 3 5;1/3 1 4;1/5 1/4 1];
[v,d]=eig(B3);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil4=(lamda-3)/2;
cr4=cil4/0.58;
b4w=v(:,1)/sum(v(:,1))
B4=[1 1/5 3;5 1 7;1/3 1/7 1];
[v,d]=eig(B4);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil5=(lamda-3)/2;
cr5=cil5/0.58;
b5w=v(:,1)/sum(v(:,1))
b1w =0.58200.27860.08990.0495
b2w =0.53960.29700.1634
b3w =0.10560.74450.1499
b4w =0.62670.27970.0936
b5w =0.18840.73060.0810A=[1 1 1 4 1 1/2;1 1 2 4 1 1/2;1 1/2 1 5 3 1/2;1/4
1/4 1/5 1 1/3 1/3;1 1 3 1/3 1 1;2 2 2 3 1 1];
[v,d]=eig(A);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil1=(lamda-6)/5;
cr1=cil1/0.90;
b1w=v(:,1)/sum(v(:,1))
B1=[1 1/4 1/2;4 1 3;2 1/3 1];
[v,d]=eig(B1);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil2=(lamda-3)/2;
cr2=cil2/0.58;
b2w=v(:,1)/sum(v(:,1))
B2=[1 1/4 1/4;4 1 1/2;5 2 1];
[v,d]=eig(B2);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil3=(lamda-3)/2;
cr3=cil3/0.58;
b3w=v(:,1)/sum(v(:,1))
B3=[1 3 1/3;1/3 1 1;3 1 1];
[v,d]=eig(B3);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil4=(lamda-3)/2;
cr4=cil4/0.58;
b4w=v(:,1)/sum(v(:,1))
B4=[1 1 7;1 1 7;1/7 1/7 1];
[v,d]=eig(B4);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil5=(lamda-3)/2;
cr5=cil5/0.58;
b5w=v(:,1)/sum(v(:,1))
B5=[1 7 9;1/7 1 5;1/9 1/5 1];
[v,d]=eig(B5);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil6=(lamda-3)/2;
cr6=cil6/0.58;
b6w=v(:,1)/sum(v(:,1))
B6=[1 1/3 5;3 1 7;1/5 1/7 1];
[v,d]=eig(B6);
eigenvalue=diag(d);
lamda=max(eigenvalue);
cil7=(lamda-3)/2;
cr7=cil6/0.58;
b7w=v(:,1)/sum(v(:,1))
b1w =0.14760.17640.19880.04490.19830.2339
b2w =0.13650.62500.2385
b3w =0.10550.33200.5625
b4w =0.3189
0.22110.4600
b5w =0.46670.46670.0667
b6w =0.77200.17340.0545
b7w =0.27900.64910.0719
全部论文及程序请见下方“ 只会建模 QQ名片” 点击QQ名片即可
相关文章:

2016年认证杯SPSSPRO杯数学建模D题(第二阶段)NBA是否有必要设立四分线全过程文档及程序
2016年认证杯SPSSPRO杯数学建模 D题 NBA是否有必要设立四分线 原题再现: NBA 联盟从 1946 年成立到今天,一路上经历过无数次规则上的变迁。有顺应民意、皆大欢喜的,比如 1973 年在技术统计中增加了抢断和盖帽数据;有应运而生、力…...
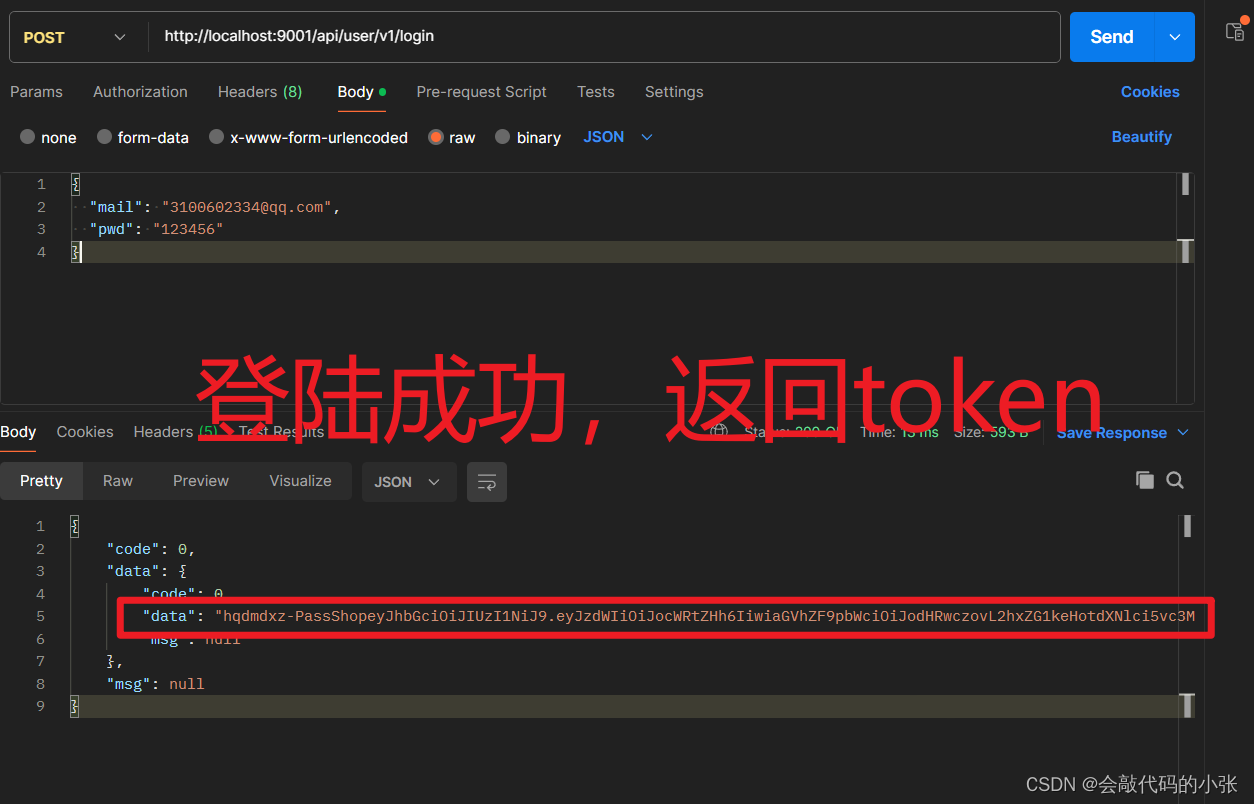
登录校验解决方案JWT
目录 🎗️1.JWT介绍 🎞️2.应用场景 🎟️3.结构组成 🎫4.JWT优点 🎠5.封装成通用方法 🛝6.JWT自动刷新 1.JWT介绍 官网:JWT官网 JSON Web Token (JWT) 是一个开放标准,它…...

Flutter开发进阶之瞧瞧BuildOwner
Flutter开发进阶之瞧瞧BuildOwner 上回说到关于Element Tree的构建还缺最后一块拼图,build的重要过程中会调用_element!.markNeedsBuild();,而markNeedsBuild会调用owner!.scheduleBuildFor(this);。 在Flutter框架中,BuildOwner负责管理构建…...
)
大量免费工具使用(提供api接口)
标题: 免费工具集使用 - 简化你的任务 介绍: 在数字化时代,我们经常需要使用各种工具来完成各种任务。本文将介绍一个免费工具集,它提供了多种实用工具,帮助简化你的任务。这些工具可以在网站 https://tool.kertennet.com 上找到…...
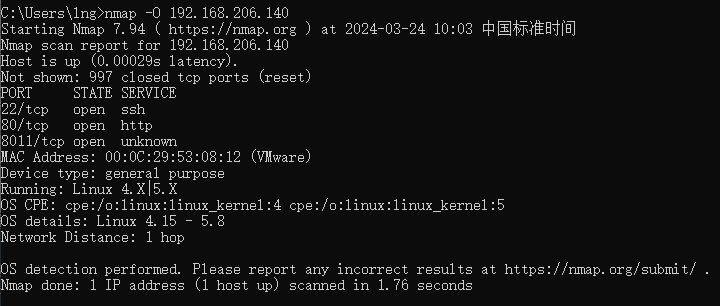
网络探测工具Nmap介绍
1. Nmap简介 Nmap是一款用于网络发现和安全审计的网络安全工具。可用于列举网络主机清单、管理服务升级调度、监控主机、监控主机服务运行状况、检测目标主机是否在线和端口开放情况、侦测运行的服务类型及版本信息、侦测操作系统与设备类型等。 2. 命令大纲 3. 命令详细介绍…...
20240319-2-机器学习基础面试题
⽼板给了你⼀个关于癌症检测的数据集,你构建了⼆分类器然后计算了准确率为 98%, 你是否对这个模型很满意?为什么?如果还不算理想,接下来该怎么做? 首先模型主要是找出患有癌症的患者,模型关注的…...

0202矩阵的运算-矩阵及其运算-线性代数
文章目录 一、矩阵的加法二、数与矩阵相乘三、矩阵与矩阵相乘四、矩阵的转置五、方阵的行列式结语 一、矩阵的加法 定义2 设有两个 m n m\times n mn橘子 A ( a i j ) 和 B ( b i j ) A(a_{ij})和B(b_{ij}) A(aij)和B(bij),那么矩阵A与B的和记为AB,规定为 A B ( a 11…...

python中的__dict__
类的__dict__返回的是:类的静态函数、类函数、普通函数、全局变量以及一些内置的属性都是放在类的__dict__里的, 而实例化对象的:__dict__中存储了一些类中__init__的一些属性值。 import的py文件 __dict__返回的是:__init__的…...

数学分析复习:无穷乘积
文章目录 无穷乘积定义:无穷乘积的收敛性命题:无穷乘积的Cauchy收敛准则正项级数和无穷乘积的联系 本篇文章适合个人复习翻阅,不建议新手入门使用 无穷乘积 设复数列 { a n } n ≥ 1 \{a_n\}_{n\geq 1} {an}n≥1,设对任意 …...

02 React 组件使用
import React, { useState } from react;// 定义一个简单的函数式组件 function Counter() {// 使用 useState hook 来创建一个状态变量 count,并提供修改该状态的函数 setCountconst [count, setCount] useState(0);// 在点击按钮时增加计数器的值const increment…...
你就是上帝
你就是上帝:Jv程序员,请你站在上帝或神的角度 1.万物皆有裂缝 按照西方文化(宗教神话,古希腊、古罗马等),上帝创建了人; 创建人之前,还创建了人的居所或地盘/栖息地(伊…...

Spring Cloud: openFegin使用
文章目录 一、OpenFeign简介二、Springboot集成OpenFeign1、引入依赖2、EnableFeignClients注解(1)应用(2)属性解析 3、 FeignClient(1)应用(2)属性解析(3)向…...

流畅的 Python 第二版(GPT 重译)(二)
第三章:字典和集合 Python 基本上是用大量语法糖包装的字典。 Lalo Martins,早期数字游牧民和 Pythonista 我们在所有的 Python 程序中都使用字典。即使不是直接在我们的代码中,也是间接的,因为dict类型是 Python 实现的基本部分。…...

Flutter 旋转动画 线性变化的旋转动画
直接上代码 图片自己添加一张就好了 import dart:math;import package:flutter/material.dart;import package:flutter/animation.dart;void main() > runApp(MyApp()); //旋转动画 class MyApp extends StatelessWidget {overrideWidget build(BuildContext context) {re…...

【Web应用技术基础】HTML(5)——案例1:展示简历信息
样式: 代码: <!DOCTYPE html> <html lang"en"> <head><meta charset"UTF-8"><meta name"viewport" content"widthdevice-width, initial-scale1.0"><title>展示简历信息…...
)
ethers.js:wallet(创建钱包,导入助记词,导入私钥)
Wallet Wallet类继承了Signer,可以使用私钥作为外部拥有帐户(EOA)的标准对交易和消息进行签名。 npm install ethers@5.4.0// 引入 import {ethers } from ethers创建新钱包 this.provider = new ethers.providers.Web3Provider(window...

面试笔记——Java集合篇
Java集合框架体系 重点:单列集合——ArrayList、LinkedList;双列集合——HashMap、ConcurrentHashMap。 List相关 数组(Array) 是一种用连续的内存空间存储相同数据类型数据的线性数据结构。 数组获取其他元素: 为什…...

在 IntelliJ IDEA 中使用 Terminal 执行 git log 命令后的退出方法
前言 IntelliJ IDEA 是一款广受欢迎的集成开发环境,它内置了强大的终端工具,使得开发者无需离开IDE就能便捷地执行各种命令行操作,包括使用 Git 进行版本控制。在 IDEA 的 Terminal 中执行 git log 命令时,由于该命令会显示项目的…...
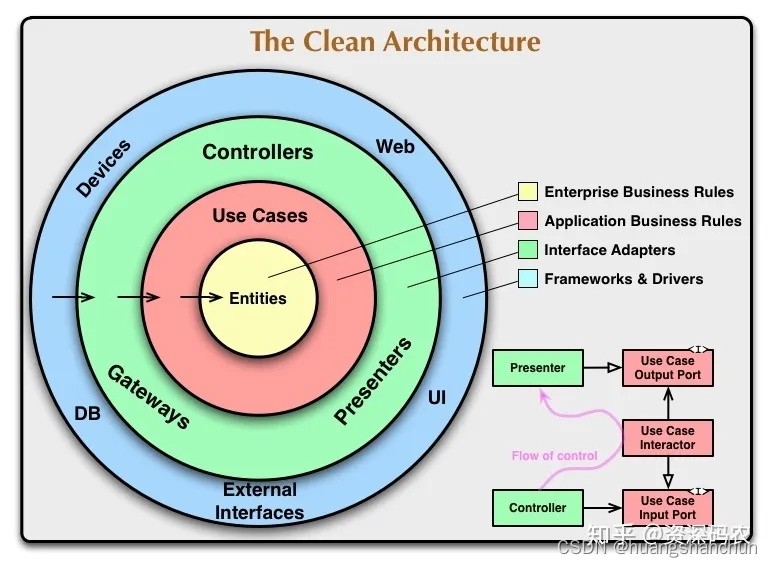
架构整洁之道-读书总结
1 概述 1.1 关于本书 《架构整洁之道》(Clean Architecture: A Craftsman’s Guide to Software Structure and Design)是由著名的软件工程师Robert C. Martin(又称为Uncle Bob)所著。这本书提供了软件开发和架构设计的指导原则…...

蓝桥杯学习笔记(贪心)
在很久很久以前,有几个部落居住在平原上,依次编号为1到n。第之个部落的人数为 t 有一年发生了灾荒,年轻的政治家小蓝想要说服所有部落一同应对灾荒,他能通过谈判来说服部落进行联台。 每次谈判,小蓝只能邀请两个部落参…...

华为云AI开发平台ModelArts
华为云ModelArts:重塑AI开发流程的“智能引擎”与“创新加速器”! 在人工智能浪潮席卷全球的2025年,企业拥抱AI的意愿空前高涨,但技术门槛高、流程复杂、资源投入巨大的现实,却让许多创新构想止步于实验室。数据科学家…...

深度学习在微纳光子学中的应用
深度学习在微纳光子学中的主要应用方向 深度学习与微纳光子学的结合主要集中在以下几个方向: 逆向设计 通过神经网络快速预测微纳结构的光学响应,替代传统耗时的数值模拟方法。例如设计超表面、光子晶体等结构。 特征提取与优化 从复杂的光学数据中自…...

Nginx server_name 配置说明
Nginx 是一个高性能的反向代理和负载均衡服务器,其核心配置之一是 server 块中的 server_name 指令。server_name 决定了 Nginx 如何根据客户端请求的 Host 头匹配对应的虚拟主机(Virtual Host)。 1. 简介 Nginx 使用 server_name 指令来确定…...

Rust 异步编程
Rust 异步编程 引言 Rust 是一种系统编程语言,以其高性能、安全性以及零成本抽象而著称。在多核处理器成为主流的今天,异步编程成为了一种提高应用性能、优化资源利用的有效手段。本文将深入探讨 Rust 异步编程的核心概念、常用库以及最佳实践。 异步编程基础 什么是异步…...

NFT模式:数字资产确权与链游经济系统构建
NFT模式:数字资产确权与链游经济系统构建 ——从技术架构到可持续生态的范式革命 一、确权技术革新:构建可信数字资产基石 1. 区块链底层架构的进化 跨链互操作协议:基于LayerZero协议实现以太坊、Solana等公链资产互通,通过零知…...

蓝桥杯3498 01串的熵
问题描述 对于一个长度为 23333333的 01 串, 如果其信息熵为 11625907.5798, 且 0 出现次数比 1 少, 那么这个 01 串中 0 出现了多少次? #include<iostream> #include<cmath> using namespace std;int n 23333333;int main() {//枚举 0 出现的次数//因…...

企业如何增强终端安全?
在数字化转型加速的今天,企业的业务运行越来越依赖于终端设备。从员工的笔记本电脑、智能手机,到工厂里的物联网设备、智能传感器,这些终端构成了企业与外部世界连接的 “神经末梢”。然而,随着远程办公的常态化和设备接入的爆炸式…...

Java线上CPU飙高问题排查全指南
一、引言 在Java应用的线上运行环境中,CPU飙高是一个常见且棘手的性能问题。当系统出现CPU飙高时,通常会导致应用响应缓慢,甚至服务不可用,严重影响用户体验和业务运行。因此,掌握一套科学有效的CPU飙高问题排查方法&…...

Netty从入门到进阶(二)
二、Netty入门 1. 概述 1.1 Netty是什么 Netty is an asynchronous event-driven network application framework for rapid development of maintainable high performance protocol servers & clients. Netty是一个异步的、基于事件驱动的网络应用框架,用于…...

【从零开始学习JVM | 第四篇】类加载器和双亲委派机制(高频面试题)
前言: 双亲委派机制对于面试这块来说非常重要,在实际开发中也是经常遇见需要打破双亲委派的需求,今天我们一起来探索一下什么是双亲委派机制,在此之前我们先介绍一下类的加载器。 目录 编辑 前言: 类加载器 1. …...
