【备战蓝桥杯】2024蓝桥杯赛前突击省一:基础数论篇
2024蓝桥杯赛前突击省一:基础算法模版篇
基础数论算法回顾
判断质数(试除法)
时间复杂度O(sqrt(n))
static int is_prime(int n){if(n<2) return 0;for (int i=2;i<=n/i;i++){if(n%i==0) return 0;}return 1;
}
质因数分解
时间复杂度O(sqrt(n))
static Map<Integer,Integer> mp = new TreeMap<>();//TreeMap有序
static void divide(int n){for(int i=2;i<=n/i;i++){int cnt = 0;//java里不能mp[i]++,所以用变量cnt存储,再赋值while(n%i==0){n/=i;cnt++;}mp.put(i,cnt);}if(n>1) mp.put(n,1);
}
//输出
for(Integer key:mp.keySet()){int val = mp.get(key);if(val>0)System.out.println(key+" "+mp.get(key));
}
素数筛
埃氏筛法
求n以内的所有素数
时间复杂度(O(nlogn))
static int[] st;
static int[] primes;
static int cnt;void get_primes(int n){for(int i=2;i<=n;i++){if(st[i]==0){primes[cnt++]=i;for(int j=i+i;j<=n;j+=i)st[j]=1;}}//求素数个数cnt
}
线性筛
void get_primes(int n)
{for (int i = 2; i <= n; i ++ ){if (!st[i]) primes[cnt ++ ] = i;for (int j = 0; primes[j] <= n / i; j ++ ){st[primes[j] * i] = true;if (i % primes[j] == 0) break;}}
}
求约数
时间复杂度 sqrt(n)
static ArrayList<Integer> yue = new ArrayList<>(); static void solve(int n){for (int i = 1; i <= n/i; i++) {if(n%i==0){yue.add(i);if(n/i!=i)yue.add(n/i);}}Collections.sort(yue);//约数从小到达排}
求组合数
求C(a,b)
用long存!!!
- N 在3000以内(题意不用取模)
static long[][] C = new long[N][N];static void init(){for (int i = 0; i < N; i++) {for (int j = 0; j <= i; j++) {if(j==0) C[i][j] = 1;else C[i][j] = C[i-1][j] + C[i-1][j-1];//对于要对答案取模的时候,在计算组合数的时候就要取模//else C[i][j] = (C[i-1][j] + C[i-1][j-1])%Mod;}}}
-
N在10^8以内、题目说要取模(用逆元求)
C(a,b) = a!/(b! * (a-b)!) = a! * niyuan(b!) * niyuan((a-b)!)由于询问比较多,直接初始化阶乘和阶乘的逆元数组
递推式:
n! = (n-1)! * n
1/(n!) = 1/(n-1)! * 1/n,其中1/n = qpow(n,Mod-2)(费马小定理)
//jiechen[i] = i!static long[] jiechen = new long[N];//jiechenniyuan[i] = “i!的逆元”static long[] jiechenniyuan = new long[N];//初始化阶乘、阶乘的逆元static void init() {jiechen[0] = 1;jiechenniyuan[0] = 1;for(int i=1;i<N;i++) {jiechen[i] = jiechen[i-1] * i%Mod;jiechenniyuan[i] = jiechenniyuan[i-1] * qpow(i, Mod-2)%Mod;}}//C(a,b) = a!/(b! * (a-b)!) = a! * niyuan(b!) * niyuan((a-b)!)static long C(int a,int b) {long res = 1;res = res * jiechen[a]%Mod;res = res * jiechenniyuan[b]%Mod;res = res * jiechenniyuan[a-b]%Mod;return res;}
https://www.acwing.com/activity/content/code/content/5904493/
扩展欧几里得算法
裴蜀定理
- 若a,b是整数,且gcd(a,b)=d,那么对于任意的整数x,y,都有ax+by都一定是d的倍数。(充要的)
特别地,一定存在整数x,y,使ax+by=d成立。
换句话说:
- 两个整数a,b,方程
a*x+b*y=m有解,当且仅当m是gcd(a,b)的倍数(充要)
扩展欧几里得代码:
// 求x, y,使得ax + by = gcd(a, b)
// 扩展欧几里得:求解方程ax+by=gcd(a,b)的解
// x=y′ y=x′−[a/b]*y′
static int x, y;//全局变量,替代引用
int exgcd(int a,int b){if(b==0){x=1,y=0;return a;}int gcd=exgcd(b,a%b);//递归调用int tmp = x;x=y,y=tmp-a/b*y;return gcd;
}//结果说明1.exgcd()的返回值是最大公约数2.最后的(x,y)是方程ax + by = gcd(a,b)的解3.如果exgcd()的结果是1(那么a和b互质,就存在逆元),那么x是a的逆元(x可能是负数,所以答案是getMod(x))
费马小定理
描述:
如果一个数p是质数,并且a不是p的倍数,那么有a^(p-1) = 1 (mod p)。
除以p同余
等价于:(推荐)
如果一个数p是质数,并且a和p互质(等价于gcd(a,p)=1),那么有a^(p-1) = 1 (mod p)
相关文章:

【备战蓝桥杯】2024蓝桥杯赛前突击省一:基础数论篇
2024蓝桥杯赛前突击省一:基础算法模版篇 基础数论算法回顾 判断质数(试除法) 时间复杂度O(sqrt(n)) static int is_prime(int n){if(n<2) return 0;for (int i2;i<n/i;i){if(n%i0) return 0;}return 1; }质因…...

golang es查询的一些操作,has_child,inner_hit,对索引内父子文档的更新
1.因为业务需要查询父文档以及其下子文档,搞了很久才理清楚。 首先还是Inner_hits,inner_hits只能用在nested,has_child,has_parents查询里面 {"query": {"nested": {"path": "comments","query": {"match…...

精准备份:如何自动化单个MySQL数据库的备份过程
自动化备份对于维护数据库的完整性和安全性至关重要。本指南将向您展示如何使用Shell脚本来自动化MySQL数据库的备份过程。 备份脚本内容 首先,这是我们将使用的备份脚本: #!/bin/bash# 完成数据库的定时备份 # 备份路径 BACKUP/data/backup/db # 当前…...
Green Hills 自带的MULTI调试器查看R7芯片寄存器
Green Hills在查看芯片寄存器时需要导入 .grd文件。下面以R7为例,演示一下过程。 首先打开MULTI调试器,如下所示View->Registers: 进入如下界面,选择导入寄存器定义文件.grd: 以当前R7芯片举例(dr7f7013…...
Jupyter Notbook如何安装配置并结合内网穿透实现无公网IP远程连接使用
文章目录 推荐1.前言2.Jupyter Notebook的安装2.1 Jupyter Notebook下载安装2.2 Jupyter Notebook的配置2.3 Cpolar下载安装 3.Cpolar端口设置3.1 Cpolar云端设置3.2.Cpolar本地设置 4.公网访问测试5.结语 推荐 前些天发现了一个巨牛的人工智能学习网站,通俗易懂&am…...
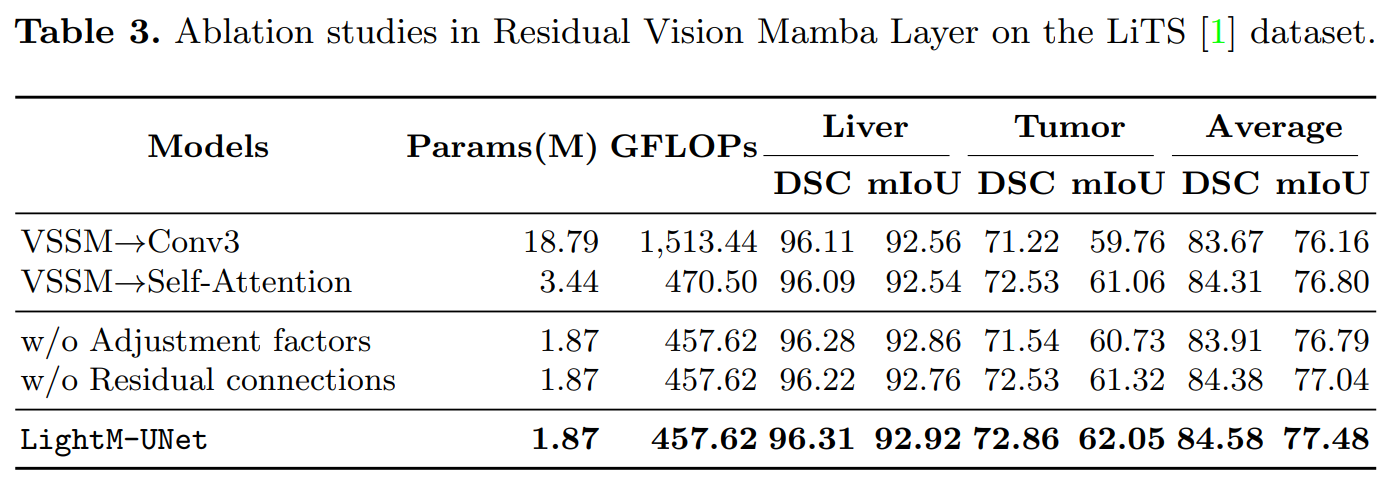
LightM-UNet:Mamba 辅助的轻量级 UNet 用于医学图像分割
文章目录 摘要1 简介2、方法论2.1、架构概述2.2、编码器块2.3、瓶颈块2.4、解码器块 3、实验4、结论 摘要 https://arxiv.org/pdf/2403.05246.pdf UNet及其变体在医学图像分割中得到了广泛应用。然而,这些模型,特别是基于Transformer架构的模型…...
探索 Java 网络爬虫:Jsoup、HtmlUnit 与 WebMagic 的比较分析
1、引言 在当今信息爆炸的时代,网络数据的获取和处理变得至关重要。对于 Java 开发者而言,掌握高效的网页抓取技术是提升数据处理能力的关键。本文将深入探讨三款广受欢迎的 Java 网页抓取工具:Jsoup、HtmlUnit 和 WebMagic,分析…...

day16 java object中equals、finalize、
Object类 1.Object类是所有类的父类。 2.一个类如果没有显示继承其它类默认继承Object类equals方法 1.Object中的equals方法 - 用来比较地址值 public boolean equals(Object obj) { return (this obj); } 2.像核心类库中的许多类都重写了equals方法(比如&…...
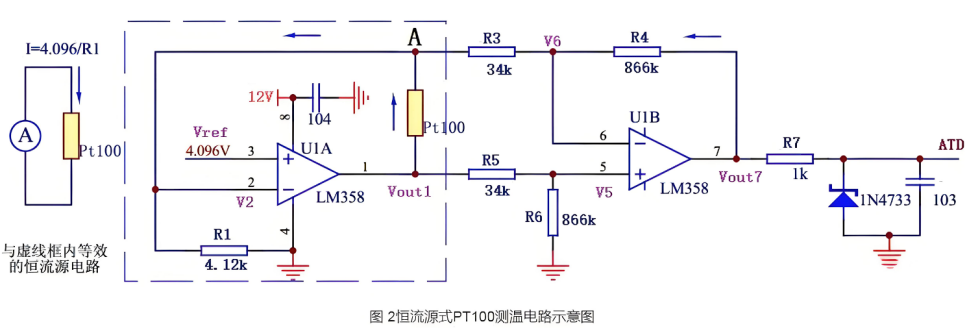
如何应用电桥电路的原理?
电桥电路是一种常用的测量技术,它利用了四个电阻的网络来检测电路的平衡状态。在平衡状态下,电桥的输出电压为零,这种特性使得电桥电路非常适合于精确测量电阻、电感、电容等电气参数,以及用于传感器和测量设备中。以下是电桥电路…...

大话设计模式——24.迭代器模式(Iterator Pattern)
简介 提供一种方法顺序访问一个聚合对象中各个元素,而又不暴露该对象的内部实现。(Java中使用最多的设计模式之一) UML图 应用场景 Java的集合对象:Collection、List、Map、Set等都有迭代器Java ArrayList的迭代器源码 示例 简…...

【数据结构】双向链表 C++
一、什么是双向链表 1、定义 双向链表也叫双链表,是链表的一种,它的每个数据结点中都有两个指针,分别指向直接后继和直接前驱。所以,从双向链表中的任意一个结点开始,都可以很方便地访问它的前驱结点和后继结点。 双…...
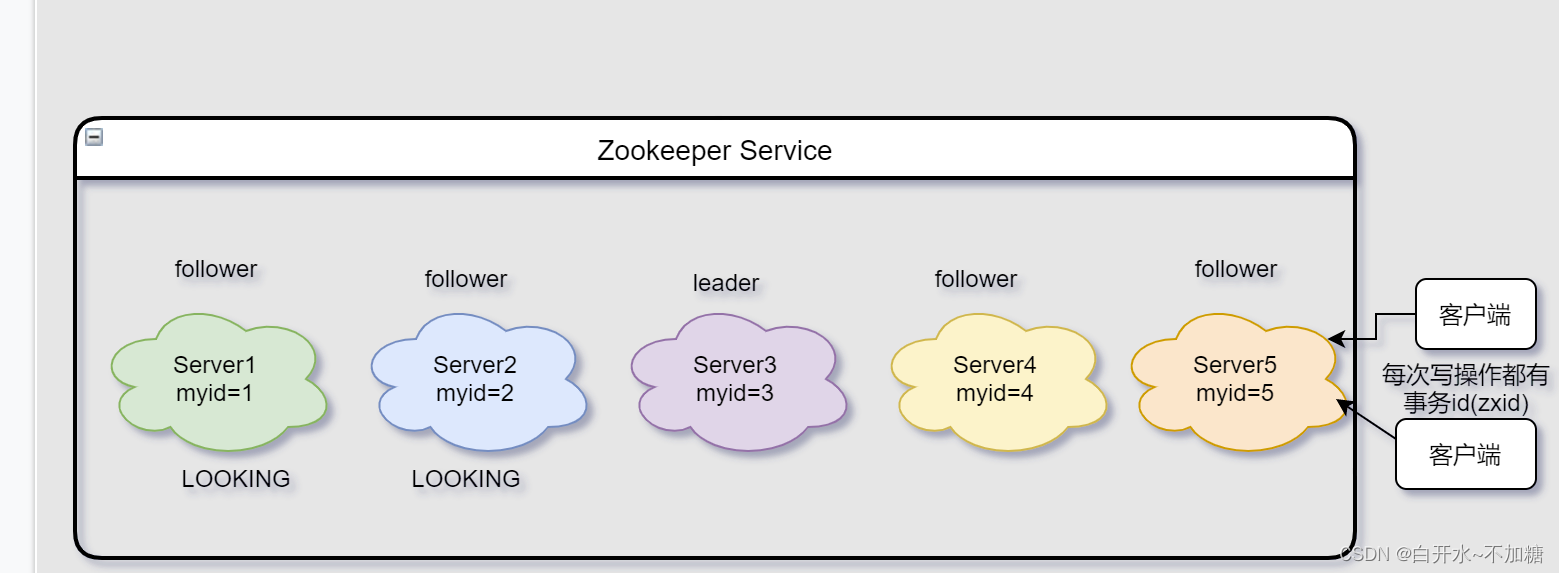
消息队列之-----------------zookeeper机制
目录 一、ZooKeeper是什么 二、ZooKeeper的工作机制 三、ZooKeeper特点 四、ZooKeeper数据结构 五、ZooKeeper应用场景 5.1统一命名服务 5.2统一配置管理 5.3统一集群管理 5.4服务器动态上下线 5.5软负载均衡 六、ZooKeeper的选举机制 6.1第一次启动选举机制 6.2非…...
第十届蓝桥杯大赛个人赛省赛(软件类) CC++ 研究生组2.0
A立方和 #include<iostream> #include<cmath> using namespace std; int main(){int n, t, flag, x;long long ans 0;for(int i 1; i < 2019; i){t i;flag 0;while(t && !flag){x t % 10;if(x 2 || x 0 || x 1 || x 9) flag 1;t / 10;}if(fl…...
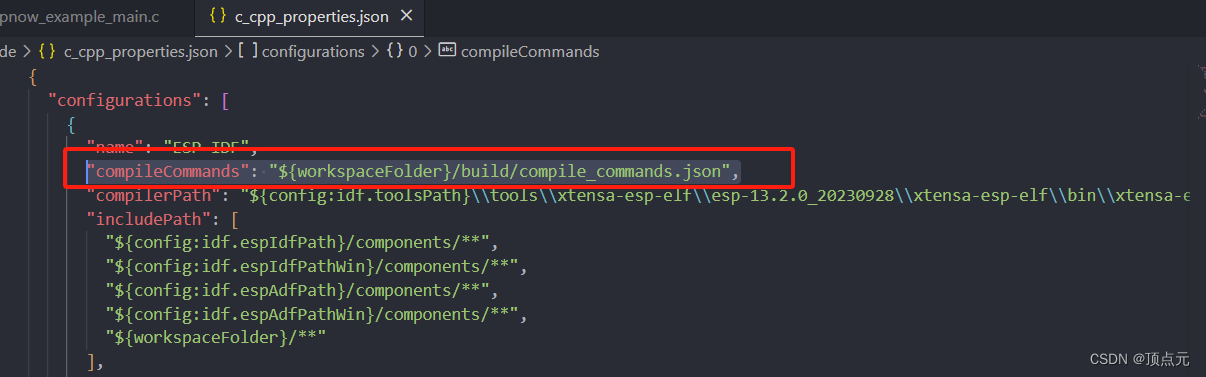
vscode开发ESP32问题记录
vscode 开发ESP32问题记录 1. 解决vscode中的波浪线警告 1. 解决vscode中的波浪线警告 参考链接:https://blog.csdn.net/fucingman/article/details/134404485 首先可以通过vscode 中的IDF插件生成模板工程,这样会自动创建.vscode文件夹中的一些json配…...
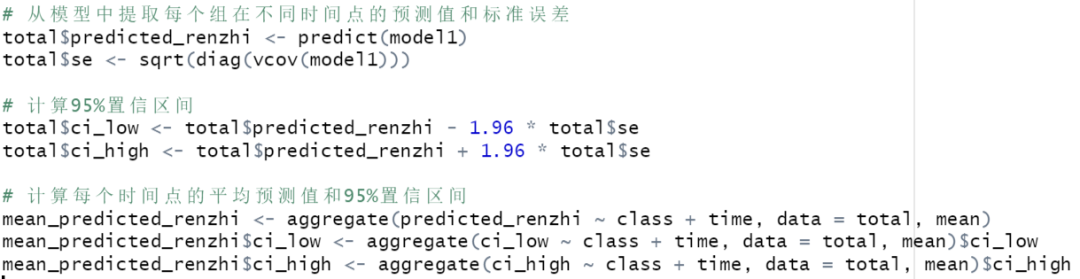
R语言复现:轨迹增长模型发表二区文章 | 潜变量模型系列(2)
培训通知 Nhanes数据库数据挖掘,快速发表发文的利器,你来试试吧!欢迎报名郑老师团队统计课程,4.20直播。 案例分享 2022年9月,中国四川大学学者在《Journal of Psychosomatic Research》(二区,I…...

【数据结构】顺序表的实现——动态分配
🎈个人主页:豌豆射手^ 🎉欢迎 👍点赞✍评论⭐收藏 🤗收录专栏:数据结构 🤝希望本文对您有所裨益,如有不足之处,欢迎在评论区提出指正,让我们共同学习、交流进…...

3.3.k8s搭建-rancher RKE2
目录 RKE2介绍 k8s集群搭建 搭建k8s集群 下载离线包 部署rke2-server 部署rke2-agent 部署helm 部署rancher RKE2介绍 RKE2,也称为 RKE Government,是 Rancher 的下一代 Kubernetes 发行版。 官网地址:Introduction | RKE2 k8s集群搭…...
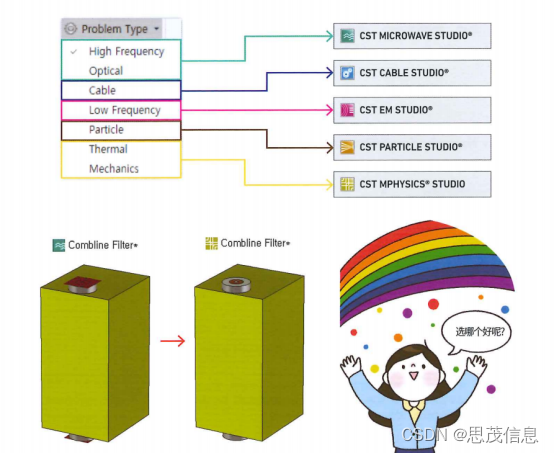
CST电磁仿真软件的设置变更与问题【官方教程】
保存结果的Result Navigator 积累的结果一目了然! 用户界面上的Result Navigator 在一个仿真工程中更改变量取值进行仿真分析或者改变设置进行仿真分析时,之前的1DResult会不会消失呢? 1D Result:CST中1D Result指的是Y值取决…...
保研线性代数复习3
一.基底(Basis) 1.什么是生成集(Generating Set)?什么是张成空间(Span)? 存在向量空间V(V,,*),和向量集(xi是所说的列向量ÿ…...

从零开始学Spring Boot系列-集成MyBatis-Plus
在Spring Boot应用开发中,MyBatis-Plus是一个强大且易于使用的MyBatis增强工具,它提供了很多实用的功能,如代码生成器、条件构造器、分页插件等,极大地简化了MyBatis的使用和配置。本篇文章将指导大家如何在Spring Boot项目中集成…...

Qt Widget类解析与代码注释
#include "widget.h" #include "ui_widget.h"Widget::Widget(QWidget *parent): QWidget(parent), ui(new Ui::Widget) {ui->setupUi(this); }Widget::~Widget() {delete ui; }//解释这串代码,写上注释 当然可以!这段代码是 Qt …...

Golang dig框架与GraphQL的完美结合
将 Go 的 Dig 依赖注入框架与 GraphQL 结合使用,可以显著提升应用程序的可维护性、可测试性以及灵活性。 Dig 是一个强大的依赖注入容器,能够帮助开发者更好地管理复杂的依赖关系,而 GraphQL 则是一种用于 API 的查询语言,能够提…...

[10-3]软件I2C读写MPU6050 江协科技学习笔记(16个知识点)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16...

ElasticSearch搜索引擎之倒排索引及其底层算法
文章目录 一、搜索引擎1、什么是搜索引擎?2、搜索引擎的分类3、常用的搜索引擎4、搜索引擎的特点二、倒排索引1、简介2、为什么倒排索引不用B+树1.创建时间长,文件大。2.其次,树深,IO次数可怕。3.索引可能会失效。4.精准度差。三. 倒排索引四、算法1、Term Index的算法2、 …...

土地利用/土地覆盖遥感解译与基于CLUE模型未来变化情景预测;从基础到高级,涵盖ArcGIS数据处理、ENVI遥感解译与CLUE模型情景模拟等
🔍 土地利用/土地覆盖数据是生态、环境和气象等诸多领域模型的关键输入参数。通过遥感影像解译技术,可以精准获取历史或当前任何一个区域的土地利用/土地覆盖情况。这些数据不仅能够用于评估区域生态环境的变化趋势,还能有效评价重大生态工程…...
)
相机Camera日志分析之三十一:高通Camx HAL十种流程基础分析关键字汇总(后续持续更新中)
【关注我,后续持续新增专题博文,谢谢!!!】 上一篇我们讲了:有对最普通的场景进行各个日志注释讲解,但相机场景太多,日志差异也巨大。后面将展示各种场景下的日志。 通过notepad++打开场景下的日志,通过下列分类关键字搜索,即可清晰的分析不同场景的相机运行流程差异…...

Unit 1 深度强化学习简介
Deep RL Course ——Unit 1 Introduction 从理论和实践层面深入学习深度强化学习。学会使用知名的深度强化学习库,例如 Stable Baselines3、RL Baselines3 Zoo、Sample Factory 和 CleanRL。在独特的环境中训练智能体,比如 SnowballFight、Huggy the Do…...

基于matlab策略迭代和值迭代法的动态规划
经典的基于策略迭代和值迭代法的动态规划matlab代码,实现机器人的最优运输 Dynamic-Programming-master/Environment.pdf , 104724 Dynamic-Programming-master/README.md , 506 Dynamic-Programming-master/generalizedPolicyIteration.m , 1970 Dynamic-Programm…...

React---day11
14.4 react-redux第三方库 提供connect、thunk之类的函数 以获取一个banner数据为例子 store: 我们在使用异步的时候理应是要使用中间件的,但是configureStore 已经自动集成了 redux-thunk,注意action里面要返回函数 import { configureS…...

Linux中《基础IO》详细介绍
目录 理解"文件"狭义理解广义理解文件操作的归类认知系统角度文件类别 回顾C文件接口打开文件写文件读文件稍作修改,实现简单cat命令 输出信息到显示器,你有哪些方法stdin & stdout & stderr打开文件的方式 系统⽂件I/O⼀种传递标志位…...
