【论文笔记】KAN: Kolmogorov-Arnold Networks 全新神经网络架构KAN,MLP的潜在替代者
KAN: Kolmogorov-Arnold Networks

code:https://github.com/KindXiaoming/pykan
Background
多层感知机(MLP)是机器学习中拟合非线性函数的默认模型,在众多深度学习模型中被广泛的应用。但MLP存在很多明显的缺点:
- **参数量大:**Transformer中,MLP几乎消耗了所有非嵌入参数。
- **缺乏可解释性:**在没有后期分析工具的情况下,相较于注意力层通常难以解释。
Novelty
受到Kolmogorov-Arnold 表示定理启发,提出了一种有希望的MLP替代方案,称为Kolmogorov-Arnold Networks(KANs)。
MLP将固定的激活函数放在节点(“神经元”)上,而KAN将可学习的激活函数放在边缘(“权重”)上。
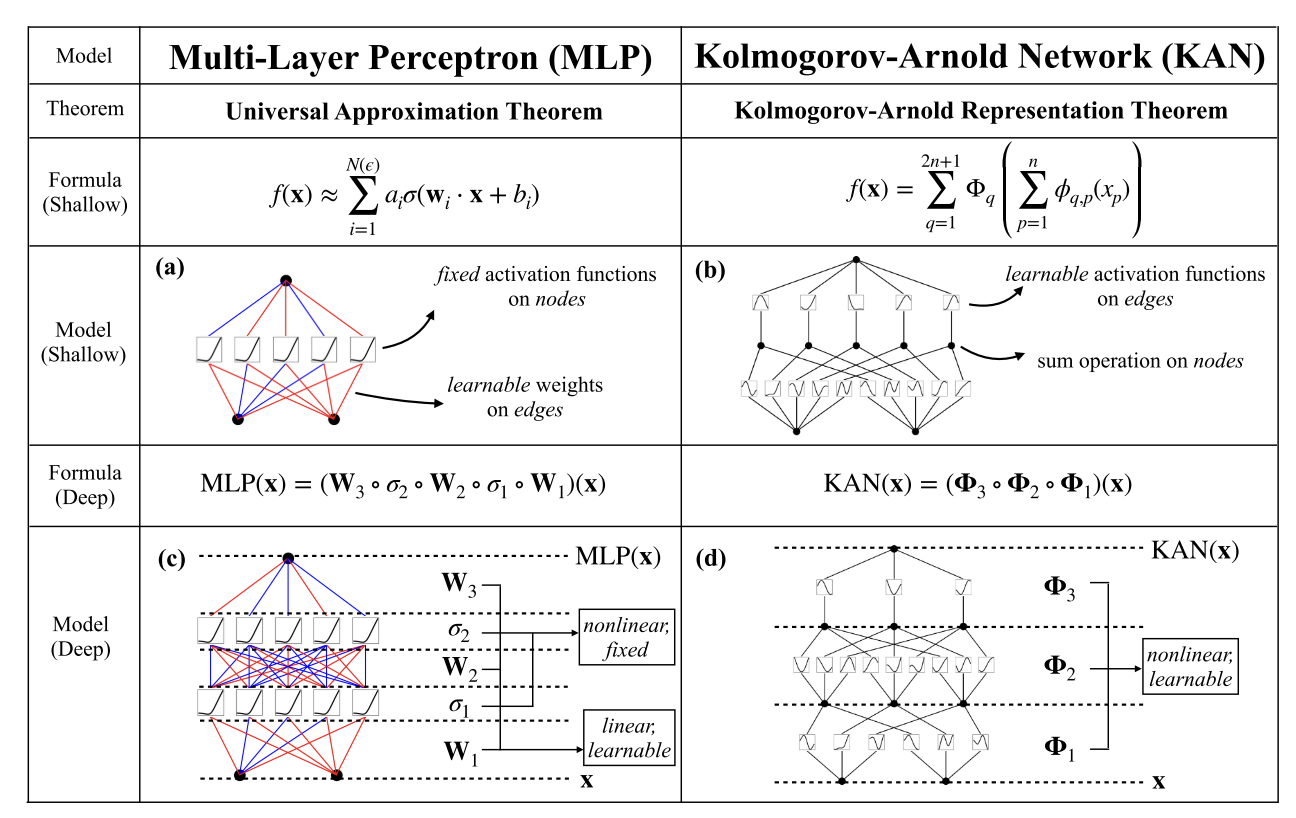
对于PDE求解,2x10 的KAN比4x100 MLP精确100倍(10−7 vs 10−5 MSE),参数效率高100倍( 1 0 2 10^2 102 vs 1 0 4 10^4 104参数)。
Method
Kolmogorov-Arnold表示定理
基本形式:
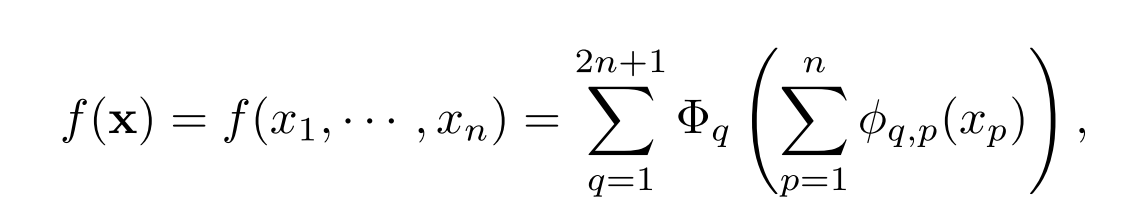
这个公式仅仅包含两层非线性和少量的隐藏层项(2n+1)。这意味着原始的表示方法虽然理论上是完备的,但在处理实际问题时可能因表达能力受限而不够有效。
本文将把网络泛化到任意宽度和深度,可以增加模型的复杂度和学习能力,使得网络能够更好地逼近和表达各种复杂的函数。
KAN结构
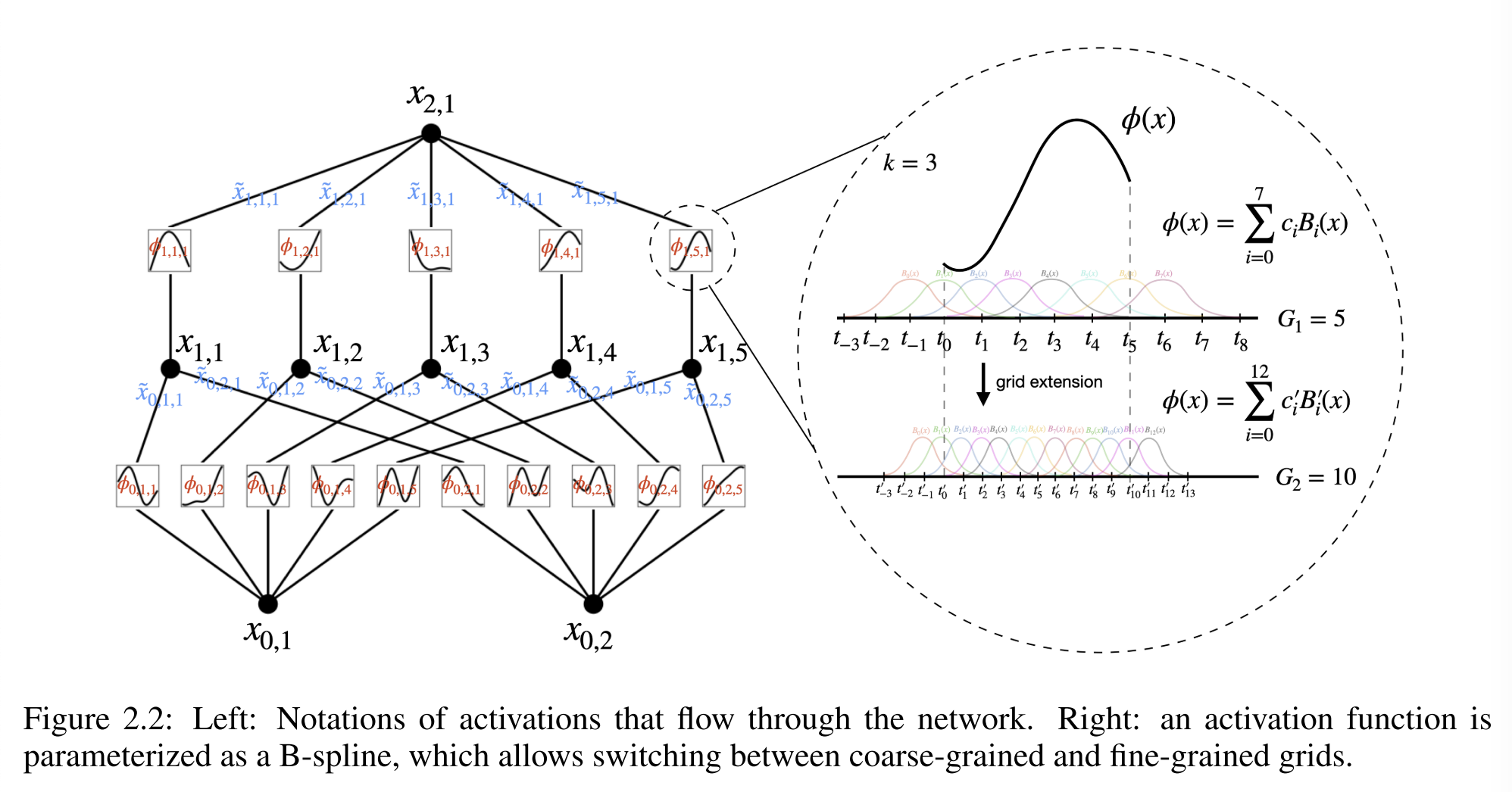
把网络泛化到任意宽度和深度:
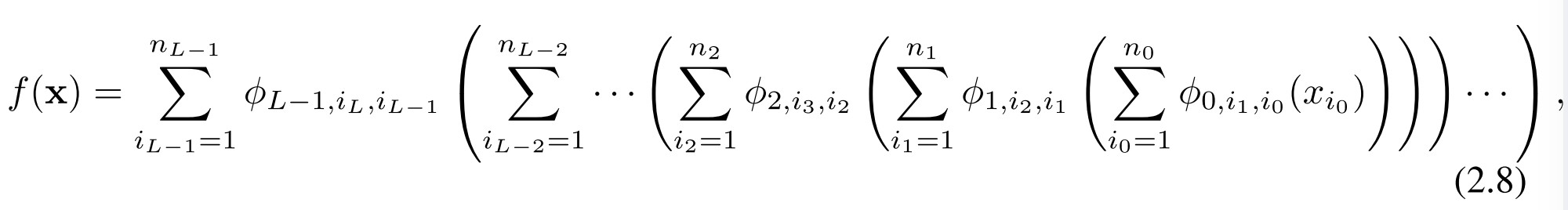
激活函数:

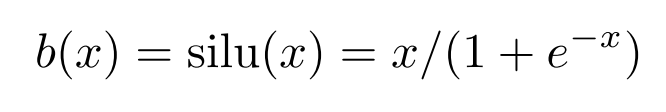
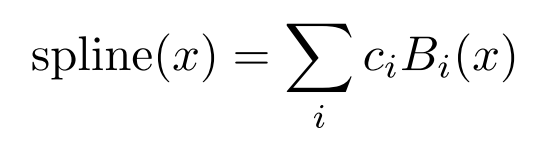
c i c_i ci是可训练的。原则上w是多余的,因为它可以被包括到b(x)和spline(x)中。然而,KAN中仍使用了w,以更好地控制激活函数的总体大小。
初始化:
每个激活函数初始化为 s p l i n e ( x ) ≈ 0 spline(x)≈0 spline(x)≈0。w根据Xavier初始化进行初始化。
网格扩展
增加MLP的宽度和深度可以提高性能,但不同大小的MLP训练是独立的,训练这些模型的成本很高。
KAN可以先用一个参数较少的模型进行训练,然后通过使其样条网格更精细,将其扩展到具有更多参数的KAN,而不需要从头开始重新训练更大的模型。通过以下公式利用最小二乘法来获得细网格的参数:
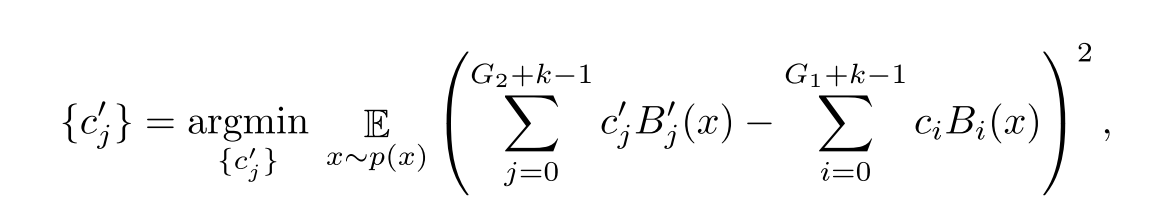
简化KAN
从一个足够大的KAN开始,用稀疏性正则化训练它,然后进行修剪。
稀疏化
在训练MLP时通常使用L1范数来鼓励模型的权重向量中有更多的零,从而达到稀疏化的效果。但L1不足以使KAN稀疏化,需要一个额外的熵正则化。
定义每一个激活函数的L1范数为:
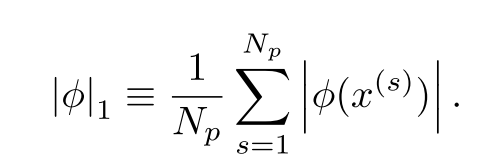
KAN的每一层的L1范数为所有激活函数的L1范数之和:
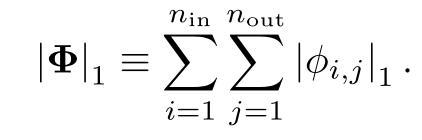
定义KAN的每一层的熵为:
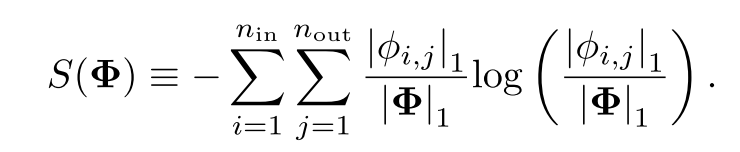
总的训练损失为预测损失与所有KAN层的L1和熵正则化之和:
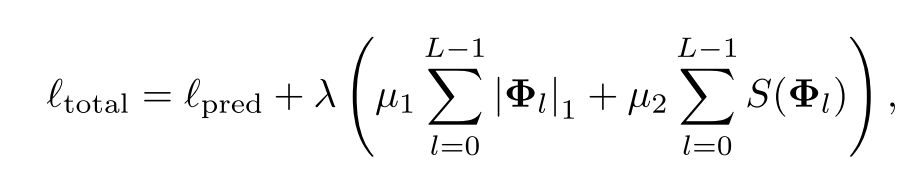
剪枝
对于每个节点来对KAN进行剪枝,定义每个结点的传入和传出分数为:
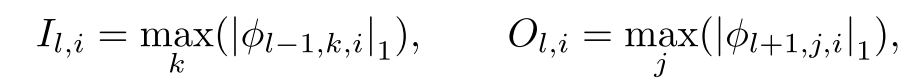
如果传入和传出的分数都小于0.01,则认为该神经元时不重要的,将其修剪。
符号化
一些激活函数实际上是符号函数(如cos、log等),作者提供了一个接口来将他们设置为制定的符号函数f的形式。但激活函数的输出和输出可能有偏移和缩放,因此从样本中获取预激活值x和后激活值y,并拟合仿射函数 y ≈ c f ( a x + b ) + d y≈cf(ax+b)+d y≈cf(ax+b)+d。

人类用户可以通过观察KAN可视化的激活函数,猜出这些符号公式,并将这些激活函数直接设置为该公式,再去拟合仿射函数。通过这样注入人类的归纳偏差或领域知识使得拟合的结果更加精准。
Experiment
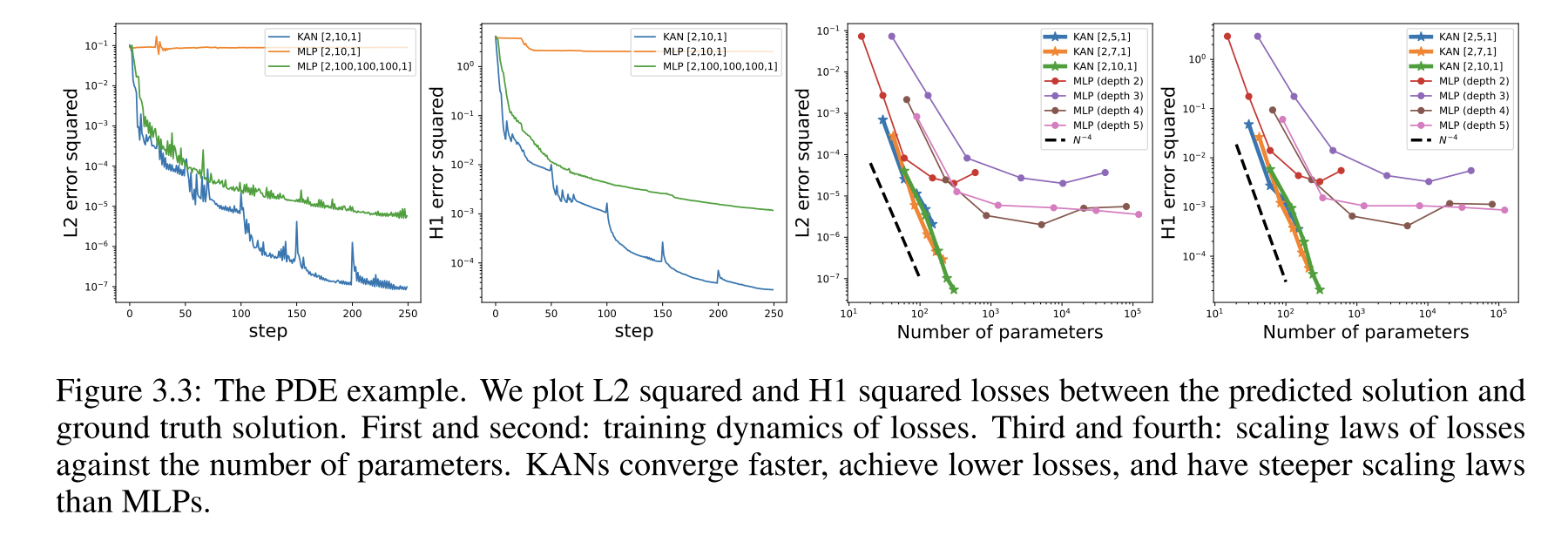
神经标度律(scaling law):KAN比MLP有着更快的标度变化速度。在求解偏微分方程任务中,KANs也展现出更快的收敛速度、达到更低的损失,并有着更陡峭的标度率表现。
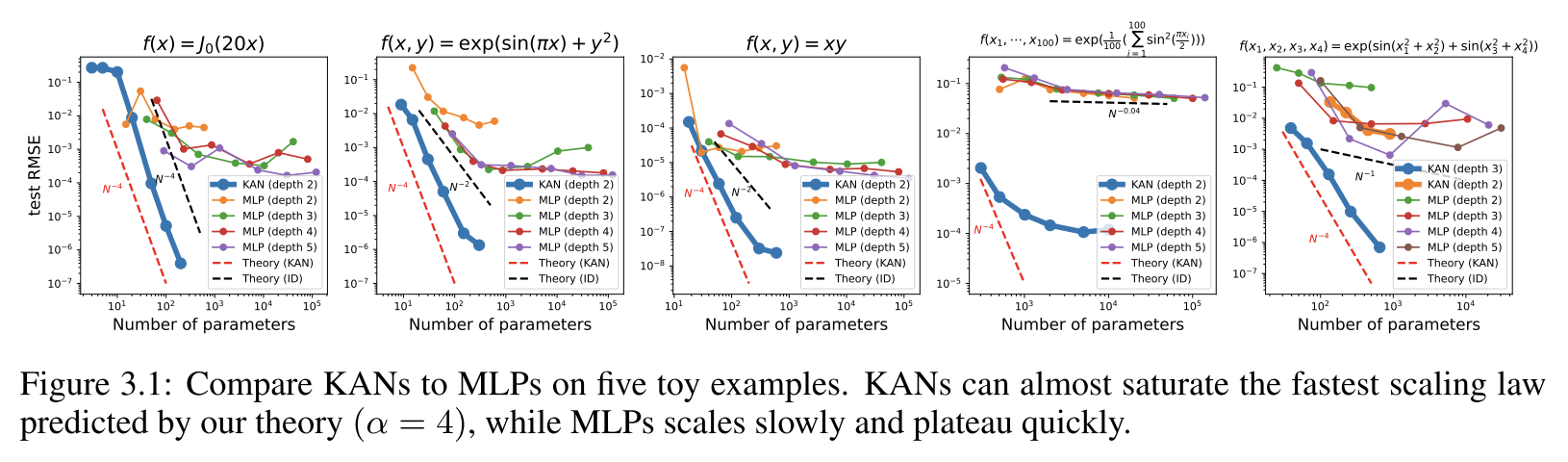
**函数拟合:**KAN比MLP更准确,具有更好的Pareto边界
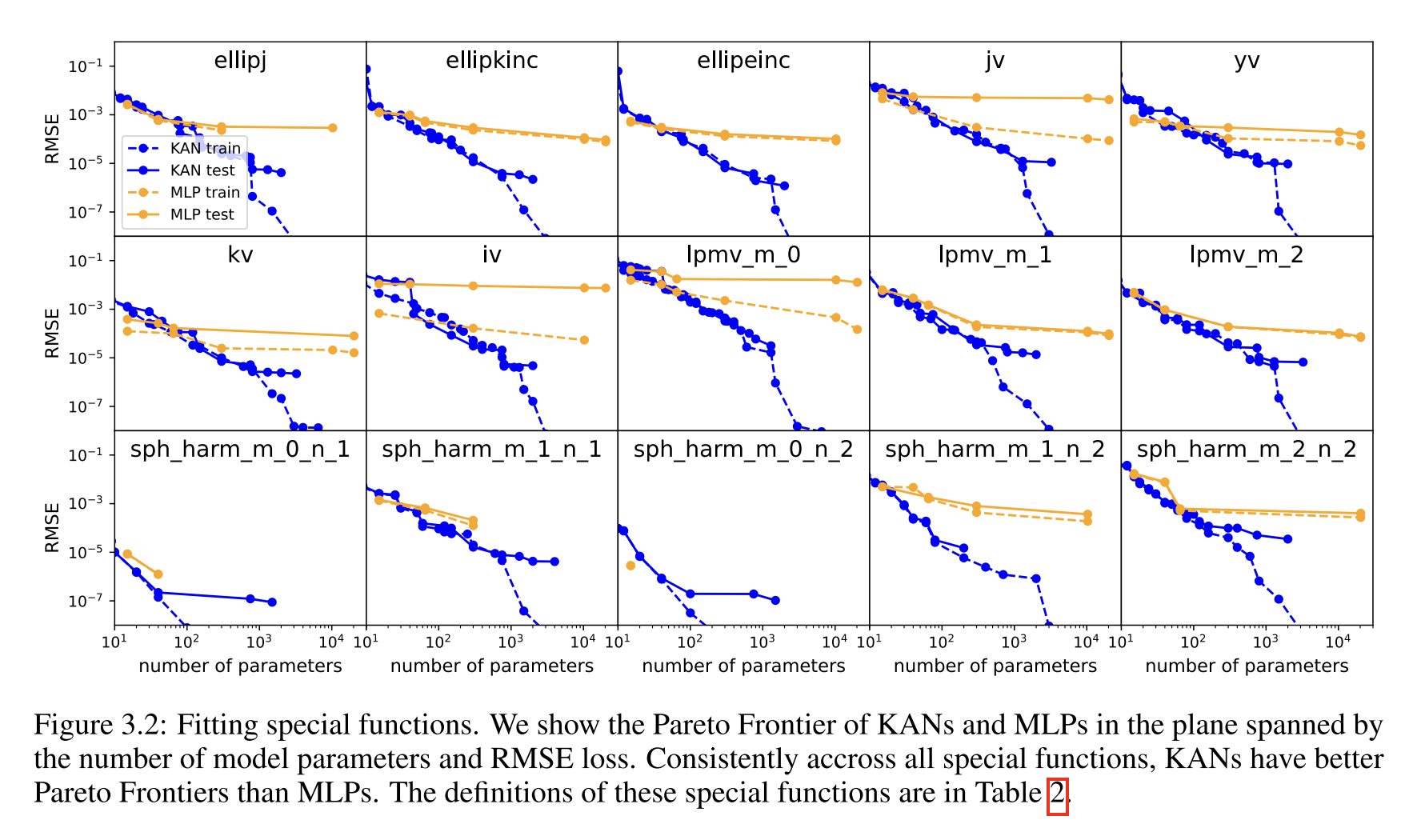
**偏微分方程求解:**在求解泊松方程时,KAN比MLP更准确,敛速度更快,损失更低,并且具有更陡峭的神经标度率表现。
**持续学习:**借助样条设计的局部性天然优势,KAN可以在新数据上实现持续学习,规避了机器学习中存在的灾难性遗忘问题。

**可解释性:**KAN能通过符号公式揭示合成数据集的组成结构和变量依赖性。

人类用户可以与 KANs 交互,使其更具可解释性。在 KAN 中注入人类的归纳偏差或领域知识非常容易。
Limitation
KAN最大的瓶颈在于训练速度慢。在参数数量相同的情况下,KAN通常比MLP慢10倍,这需要在未来加以改善。
相关文章:

【论文笔记】KAN: Kolmogorov-Arnold Networks 全新神经网络架构KAN,MLP的潜在替代者
KAN: Kolmogorov-Arnold Networks code:https://github.com/KindXiaoming/pykan Background 多层感知机(MLP)是机器学习中拟合非线性函数的默认模型,在众多深度学习模型中被广泛的应用。但MLP存在很多明显的缺点:…...

【投稿资讯】区块链会议CCF C -- CoopIS 2024 截止7.10 附录用率
会议名称:CoopIS CCF等级:CCF C类学术会议 类别:人机交互与普适计算 录用率:2023年接收率21% (21 regular 10 work-in-progress papers/100) AREA 5: HUMAN-CENTRIC SECURITY AND PRIVACY IN INFORMATION SYSTEMS Access Con…...

React Native 之 开发环境搭建(一)
1. 安装Node.js: Node.js是React Native开发的基础,因此首先需要安装Node.js。强烈建议始终选择 Node 当前的 LTS (长期维护)版本,一般是偶数版本,不要选择偏实验性质的奇数版本。 如果你希望更方便地管理…...
DS高阶:B树系列
一、常见的搜索结构 1、顺序查找 时间复杂度:O(N) 2、二分查找 时间复杂度:O(logN) 要求:(1)有序 (2)支持下标的随机访问 3、二叉搜索树(BS树) 时间复杂…...

第五百零三回
文章目录 1. 概念介绍2. 使用方法2.1 普通路由2.2 命名路由 3. 示例代码4. 内容总结 我们在上一章回中介绍了"使用get显示Dialog"相关的内容,本章回中将介绍使用get进行路由管理.闲话休提,让我们一起Talk Flutter吧。 1. 概念介绍 我们在本章…...
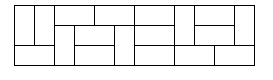
[动态规划] 完美覆盖
描述 一张普通的国际象棋棋盘,它被分成 8 乘 8 (8 行 8 列) 的 64 个方格。设有形状一样的多米诺牌,每张牌恰好覆盖棋盘上相邻的两个方格,即一张多米诺牌是一张 1 行 2 列或者 2 行 1 列的牌。那么,是否能够把 32 张多米诺牌摆放…...
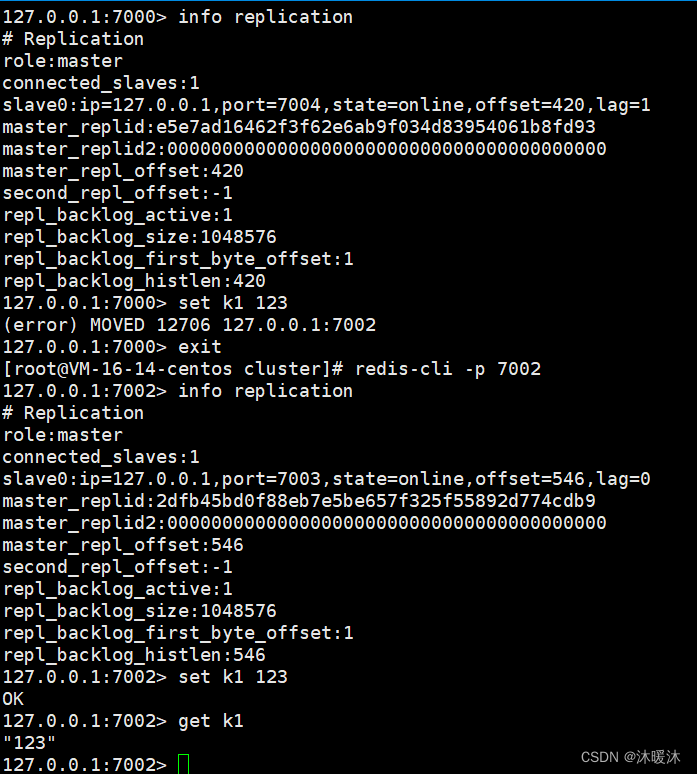
redis深入理解之实战
1、SpringBoot整合redis 1.1 导入相关依赖 <dependency><groupId>redis.clients</groupId><artifactId>jedis</artifactId> </dependency> <dependency><groupId>org.springframework.boot</groupId><artifactId&g…...

python设计模式---工厂模式
定义了一个抽象类Animal,并且让具体的动物类(Dog、Cat、Duck)继承自它,并实现了speak方法。然后创建了AnimalFactory工厂类,根据传入的参数来决定创建哪种动物的实例。 from abc import abstractmethod, ABCclass Anim…...

探索Vue 3.0中的v-html指令
探索Vue 3.0中的v-html指令 一、什么是v-html指令?1、 在Vue 3.0中使用v-html2、 注意事项 二、结语 一、什么是v-html指令? Vue.js作为一款流行的JavaScript框架,不断地演进着。随着Vue 3.0的发布,开发者们迎来了更加强大和灵活…...

anaconda 环境配置
官方网站下载地址: https://www.anaconda.com/download/ 国内清华镜像下载地址: https://mirrors.tuna.tsinghua.edu.cn/anaconda/archive/ 配置国内环境: conda config --add channels https://mirrors.tuna.tsinghua.edu.cn/anaconda/pkgs/free/ …...

DS:顺序表、单链表的相关OJ题训练(2)
欢迎各位来到 Harper.Lee 的学习世界! 博主主页传送门:Harper.Lee的博客主页 想要一起进步的uu欢迎来后台找我哦! 一、力扣--141. 环形链表 题目描述:给你一个链表的头节点 head ,判断链表中是否有环。如果链表中有某个…...
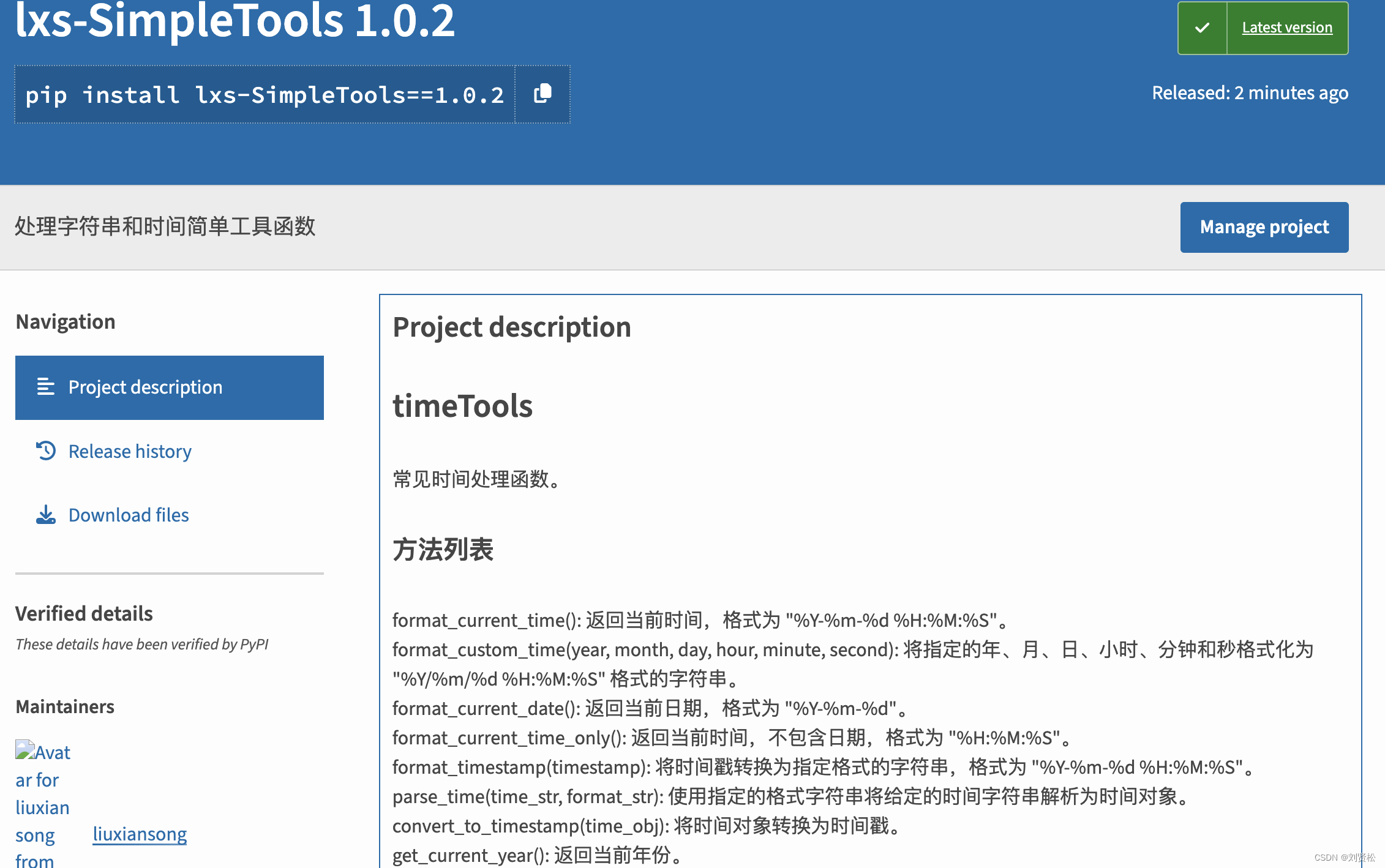
上传到 PyPI
将软件包上传到 PyPI(Python Package Index),您需要遵循以下步骤: 准备软件包:确保您的软件包满足以下要求: 包含一个 setup.py 文件,用于描述软件包的元数据和依赖项。包含软件包的源代码和必要…...
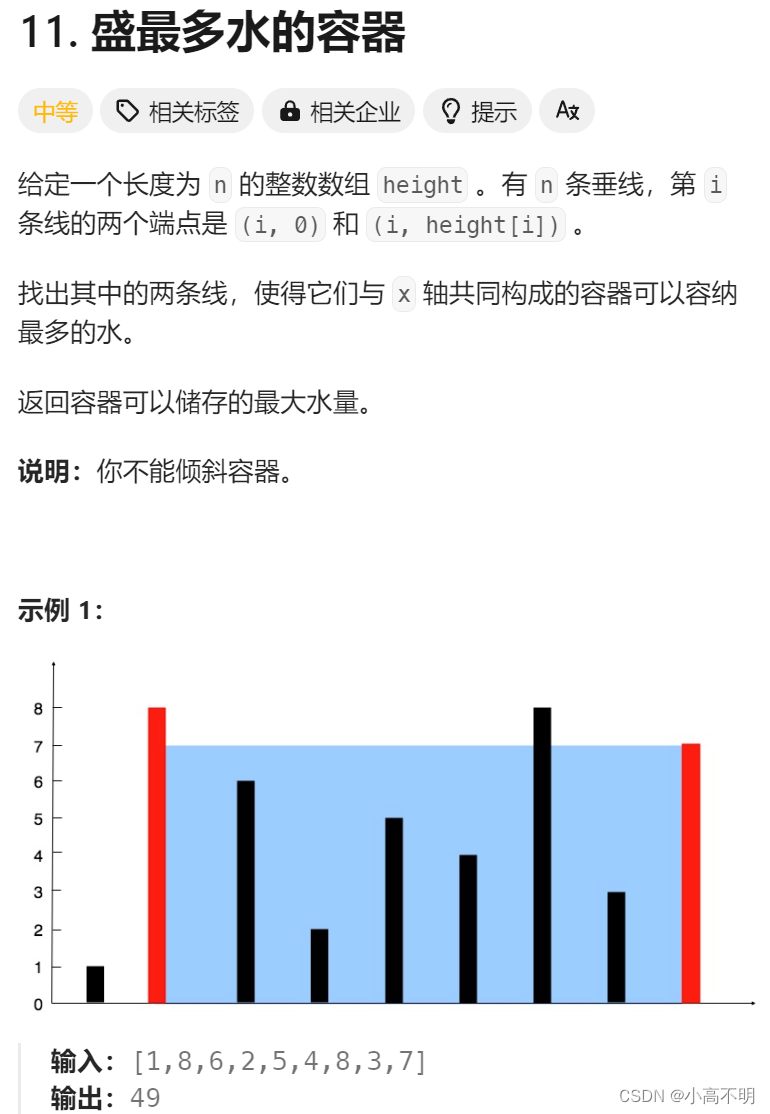
盛最多水的容器(双指针)
解题思路: 1,暴力解法(超时) 我们可以使用两层for循环进行遍历。找到那个最大的面积即可,这里我就不写代码了,因为写了也是超时。 2,双指针法 先定义两个指针一个在最左端,一个在…...
【深度学习】实验3 特征处理
特征处理 python 版本 3.7 scikit-learn 版本 1.0.2 1.标准化 from sklearn.preprocessing import StandardScaler from sklearn.preprocessing import MinMaxScaler from matplotlib import gridspec import numpy as np import matplotlib.pyplot as plt cps np.random.…...
MoneyPrinter国内版改造
背景: MoneyPrinter 是一个自动生成短视频的开源项目。只需要输入短视频主题,然后就可以生成视频。 在国内环境运行时,框架中使用的youtube、抖音文字转语音等功能无法使用,需要对框架进行国内版改造,使其使用国内网络…...

C++ 派生类的引入与特性
一 继承与派生 从上面的例子可以看出: 继承:一旦指定了某种事物父代的本质特征,那么它的子代将会自动具有哪些性质。这就是一种朴素的可重用的概念。 派生:而且子代可以拥有父代没有的特性,这是可扩充的概念。 1 C 的…...
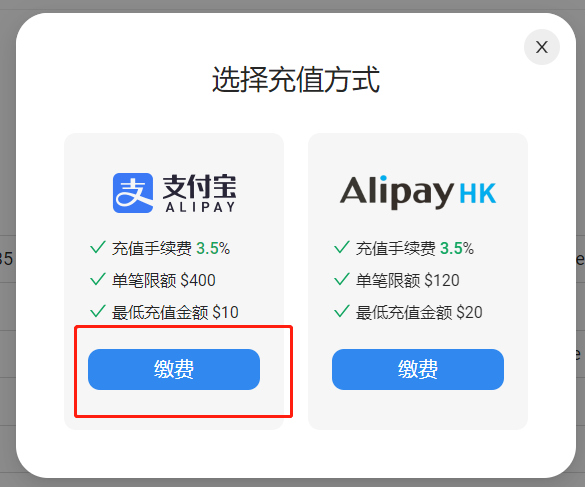
Poe是什么?怎样订阅Poe?
Poe(全称“开放探索平台”,Platform for Open Exploration)是一款由Quora开发的移动应用程序,于2022年12月推出。该应用程序内置建基于AI技术的聊天机器人,可供用户向机器人询问专业知识、食谱、日常生活,甚…...

基于FPGA的视频矩阵切换方案
一、单个显示设备的系统方案:会议室只有1个显示设备 会议室的信号源有很多,但是显示设备只有1个,这个时候最佳方案是使用切换器。 (1)切换器(控制方式:遥控器、软件、机箱面板、中控ÿ…...

.NET周刊【5月第1期 2024-05-05】
国内文章 一个开源轻量级的C#代码格式化工具(支持VS和VS Code) https://www.cnblogs.com/Can-daydayup/p/18164905 CSharpier是一个开源、免费的C#代码格式化工具,特点是轻量级且依赖Roslyn引擎重构代码格式。支持的IDE包括Visual Studio …...
springcloud -nacos实战
一、nacos 功能简介 1.1.什么是Nacos? 官方简介:一个更易于构建云原生应用的动态服务发现(Nacos Discovery )、服务配置(Nacos Config)和服务管理平台。 Nacos的关键特性包括: 服务发现和服务健康监测动态配置服务动态DNS服务服务及其元数…...

浅谈 React Hooks
React Hooks 是 React 16.8 引入的一组 API,用于在函数组件中使用 state 和其他 React 特性(例如生命周期方法、context 等)。Hooks 通过简洁的函数接口,解决了状态与 UI 的高度解耦,通过函数式编程范式实现更灵活 Rea…...

内存分配函数malloc kmalloc vmalloc
内存分配函数malloc kmalloc vmalloc malloc实现步骤: 1)请求大小调整:首先,malloc 需要调整用户请求的大小,以适应内部数据结构(例如,可能需要存储额外的元数据)。通常,这包括对齐调整,确保分配的内存地址满足特定硬件要求(如对齐到8字节或16字节边界)。 2)空闲…...

线程同步:确保多线程程序的安全与高效!
全文目录: 开篇语前序前言第一部分:线程同步的概念与问题1.1 线程同步的概念1.2 线程同步的问题1.3 线程同步的解决方案 第二部分:synchronized关键字的使用2.1 使用 synchronized修饰方法2.2 使用 synchronized修饰代码块 第三部分ÿ…...

C++ 基础特性深度解析
目录 引言 一、命名空间(namespace) C 中的命名空间 与 C 语言的对比 二、缺省参数 C 中的缺省参数 与 C 语言的对比 三、引用(reference) C 中的引用 与 C 语言的对比 四、inline(内联函数…...

【C语言练习】080. 使用C语言实现简单的数据库操作
080. 使用C语言实现简单的数据库操作 080. 使用C语言实现简单的数据库操作使用原生APIODBC接口第三方库ORM框架文件模拟1. 安装SQLite2. 示例代码:使用SQLite创建数据库、表和插入数据3. 编译和运行4. 示例运行输出:5. 注意事项6. 总结080. 使用C语言实现简单的数据库操作 在…...

AI编程--插件对比分析:CodeRider、GitHub Copilot及其他
AI编程插件对比分析:CodeRider、GitHub Copilot及其他 随着人工智能技术的快速发展,AI编程插件已成为提升开发者生产力的重要工具。CodeRider和GitHub Copilot作为市场上的领先者,分别以其独特的特性和生态系统吸引了大量开发者。本文将从功…...

【论文阅读28】-CNN-BiLSTM-Attention-(2024)
本文把滑坡位移序列拆开、筛优质因子,再用 CNN-BiLSTM-Attention 来动态预测每个子序列,最后重构出总位移,预测效果超越传统模型。 文章目录 1 引言2 方法2.1 位移时间序列加性模型2.2 变分模态分解 (VMD) 具体步骤2.3.1 样本熵(S…...

OPENCV形态学基础之二腐蚀
一.腐蚀的原理 (图1) 数学表达式:dst(x,y) erode(src(x,y)) min(x,y)src(xx,yy) 腐蚀也是图像形态学的基本功能之一,腐蚀跟膨胀属于反向操作,膨胀是把图像图像变大,而腐蚀就是把图像变小。腐蚀后的图像变小变暗淡。 腐蚀…...

SAP学习笔记 - 开发26 - 前端Fiori开发 OData V2 和 V4 的差异 (Deepseek整理)
上一章用到了V2 的概念,其实 Fiori当中还有 V4,咱们这一章来总结一下 V2 和 V4。 SAP学习笔记 - 开发25 - 前端Fiori开发 Remote OData Service(使用远端Odata服务),代理中间件(ui5-middleware-simpleproxy)-CSDN博客…...

AGain DB和倍数增益的关系
我在设置一款索尼CMOS芯片时,Again增益0db变化为6DB,画面的变化只有2倍DN的增益,比如10变为20。 这与dB和线性增益的关系以及传感器处理流程有关。以下是具体原因分析: 1. dB与线性增益的换算关系 6dB对应的理论线性增益应为&…...
